Gravitational Lensing and Wormhole Shadows

Abstract

The problem of bending and scattering of light rays passing outside the entrance of a wormhole with zero gravitational mass is considered. The process of ray capture by a wormhole, as well as the formation process of a shadow when illuminated by a standard screen, is investigated. These mechanisms are also compared to the case of light ray motion in the vicinity of the Schwarzschild black hole.

1 INTRODUCTION

Recently, issues related to the physics of wormholes (WH) have attracted the attention of specialists. This attention developed upon the hypothesis that some galactic nuclei may not be supermassive black holes (BH), but entrances to WH [1, 2]. There is a need to test this hypothesis [3], such as studying the behavior of light rays in the vicinity of the entrance of a wormhole, as well as to analyze the possibility of the appearance of a shadow, similar to the case of BH, where shadow formation does take place. All of these questions are also of fundamental importance for the theory of WH. In this article, we begin to explore these fundamental issues starting with the simplest models.

In this paper, we consider the simplest zero-mass Ellis–Bronnikov–Morris–Thorne wormhole model [4–7]. For questions of physics regarding such an unusual situation, zero gravity is everywhere and nevertheless the curvature of space and the presence of a wormhole exists; see, for example, in [6, 8]. In this paper, we study the distortion of the light ray motion passing in the vicinity of the entrance to a wormhole. We study the light ray propagation distortions caused by the wormhole in the vicinity of its entrance followed by the comparison of those distortions to the ones caused by the gravitational field of the Schwarzschild BH. Next, we construct the shadow of a wormhole illuminated by the simplest model of a light screen and compare the result once again to the case of the Schwarzschild black hole illuminated by the same screen.

The results reveal the most important features of the process. Thus, we turn to more complex and realistic situations.

When comparing the processes in WHs and BHs, we will not consider the rays passing into the wormhole. We will assume that the WH is filled with an opaque substance and the rays crossing the throat of the WH are absorbed by this substance.

The implementation of our project consists of calculating the trajectories of light beams, i.e., zero geodesics in wormhole space-time. The corresponding geodesics have been calculated and discussed many times since the pioneering work [4]; see also [9–16]. However, the problem requires a large amount of numerical simulation. Thus, we needed other forms of motion equations and an analysis of their other properties. The results of this work are given in the Appendix. Of course, the properties of geodesics in Schwarzschild space-time are well known [17, 18].

In this paper, we do not consider the issues of WH instability (see [19]) and assume that the WH metric does not depend on time.

2 BENDING OF LIGHT RAYS

Consider in the WH metric,

$$d{{s}^{2}} = d{{t}^{2}} - \frac{{{{r}^{2}}}}{{{{r}^{2}} - {{q}^{2}}}}d{{r}^{2}} - {{r}^{2}}(d{{\vartheta }^{2}} + {{\sin}^{2}}\vartheta d{{\varphi }^{2}}),$$

(1)

the classical problem of wormhole ray scattering where light arrives from infinity with impact parameter $b$.

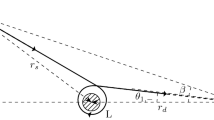
Let us recall what this problem looks like in the Schwarzschild BH metric; see Fig. 1. First of all, let us note that the BH is encompassed by a sphere influence of outer radius $r = 3{{r}_{g}}{\text{/}}2$, around which the photons can move. Beams with the impact parameter ${{b}_{{{\text{crit}}}}} = 3\sqrt 3 {{r}_{g}}{\text{/}}2$ are captured by the black hole. The beams with a slightly larger impact parameter undergo bending and can go around the BH many times in a tight spiral close to the circle $r = 3{{r}_{g}}{\text{/}}2$ before going back to infinity; see Fig. 2.

Fig. 1.

Bending of the light rays by the Schwarzschild BH. A black circle with the radius of $r = {{r}_{g}} = 2GM{\text{/}}{{c}^{2}}$ is a black hole. The dashed circle is $r = 3{{r}_{g}}{\text{/}}2$. ${{b}_{{{\text{crit}}}}} = 3\sqrt 3 {{r}_{g}}{\text{/}}2$ is the critical impact parameter of the BH beam capture. The impact parameters are indicated for each trajectory. The trajectory with an impact parameter $b = 2.59{{r}_{g}}$ enters the event horizon vertically.

Fig. 2.

Bending of the beam by the Schwarzschild black hole. The value of the impact parameter is shown in the figure. The dashed circle has the radius $r = 3{{r}_{g}}{\text{/}}2$.

Let us now turn to the curvature of light rays near the Ellis–Bronnikov–Morris–Thorne wormhole. At first glance, the overall picture should be fundamentally different from the classical one above, because the WH is massless in this case, i.e., $m = 0$—there are no gravitational forces. Therefore, the classical utterance “…under the influence of the gravitational field, the light beam is bent” [18] would be inappropriate here. In this case, the light beam is bent due to the three-dimensional bending of space itself. This curvature of space that solely determines ray bending is analyzed in detail in [20].

Figure 3, taken from the paper [20], shows a curve whose rotation around the $z$-axis gives the equatorial section surface of the WH.

Fig. 3.

The curve whose rotation about the $y$-axis forms the surface of the equatorial section of a WH. The distances are normalized to the radius of the WH throat.

The derivation of the zero geodesic equations for WH and BH Schwarzschild metrics is given in the Appendix.

The trajectories in the vicinity of a WH are shown in Fig. 4. In this case, the circular orbits of light rays are also present. They are located at the throat of the WH at $r = q$. As shown by computational analysis, the rays that arrive with an impact parameter less than ${{b}_{{{\text{crit}}}}} = q$ are captured by the wormhole and, according to our assumption, undergo absorption within it. Similar to the case of a BH, the trajectories that revolve multiple times around a WH do exist. Examples are shown in Fig. 5. These trajectories are important when constructing the WH shadow.

Fig. 4.

Trajectories of light beans near a WH. Distances are measured in the units of WH throat radius. The throat of a wormhole is shown with a dashed line. The impact parameter value is indicated for each trajectory.

Fig. 5.

Trajectories of light beams with a small impact parameter near the WH. Distances are measured in the units of WH throat radius. The impact parameter is indicated for each trajectory.

Thus, despite the absence of gravitational forces, the picture of curved light rays is qualitatively similar to the case of a BH, although it differs numerically.

3 WORMHOLE SHADOWS

The shadows created by BH against the background of various luminous formations are being studied in detail in modern theoretical astrophysics. Moreover, these shadows were recently discovered by astrophysical observations [21–26]. All these works are of great importance both for the theory and for the experimental studies of the Universe.

The construction of the theory of WH shadows is of great importance for the detection of WHs in the Universe. In this paper, we will consider the simplest examples of the theoretical computation of the WH shadow structure. We will consider the WH against the background of a distant infinite screen, radiating uniformly in all directions. Such a screen is called the Lambert source.

Recall that we consider particular rays that move outside the WH, assuming that the interior of the WH is impenetrable for light. The results of Section 2 can be used to determine the structure of the shadow that is formed.

Figure 6 shows a diagram of the corresponding computation. The parallel bundle of zero geodesic trajectories on the right is the trajectories that arrive to a distant observer. The observer sees only those trajectories that start on the screen. Other trajectories either come from infinity or from the wormhole itself, and then carry no light. Considering these latter trajectories, the shadow of the wormhole can be constructed. The image in Fig. 6 is a reversal in time from the pictures in Figs. 4, 5.

Fig. 6.

Scheme for computing the formation of the WH shadow when illuminated by a remote screen (shown in the figure on the left, coordinate $- 10$). The observer is on the far right. The distances are measured in units of the radius of the WH throat. For each trajectory, the value of the impact parameter is indicated.

Figure 7 shows the shadow of the WH and the distribution of the radiation intensity near its boundary: the so-called corona or aura. The shadow is a circle with rings (an infinite number of rings) near the inner edge of the shadow. Figure 8 shows the trajectories of zero geodesics defining the edge of the WH shadow and the first ring, i.e., the trajectories turning 90° and 270°, respectively. The impact parameters of these trajectories are as follows:

$${{b}_{{90}}} = 1.092q,\quad {{b}_{{270}}} = 1.00315q,$$

(2)

where $q$ as before denotes the radius of the WH throat. The subsequent rings correspond to the smaller values of the impact parameter, up to ${{b}_{{{\text{crit}}}}} = q$.

Fig. 7.

The shape of the WH shadow (left) and the distribution of the radiation intensity near its edge (on right). The radial coordinate is expressed in units of the radius of the WH throat.

Fig. 8.

Critical trajectories in the WH field. The radial coordinate is expressed in units of the radius of a wormhole throat.

The distribution of the radiation intensity in the equatorial section of the WH shadow is shown in Fig. 9. When approaching the shadow boundary, the radiation intensity in the corona increases by several orders of magnitude and turns out to be nonlinear on a logarithmic scale. Unfortunately, we cannot compare the intensity of the inner ring radiation with the intensity of the corona due to the limited accuracy of the computations. This requires other numerical methods.

Fig. 9.

Radiation intensity distribution in the equatorial section of the WH shadow.

Comparison with Figs. 7, 10 shows the Schwarzschild black hole shadow and the distribution of the radiation intensity in its corona against the background of the same bright screen. As follows from Fig. 10, the position of the bright ring inside the shadow silhouette is very different for the BH and the WH, and this may be one of the signs by which these objects can be distinguished from each other.

Fig. 10.

The shape of the shadow of the Schwarzschild black hole (left) and the distribution of the radiation intensity near its edge (on right). The radial coordinate is expressed in units of the gravitational radius ${{r}_{g}}2Gm{\text{/}}{{c}^{2}}$.

Another sign may be the intensity distribution in the equatorial section of the shadow of the WH and BH. For the latter, the distribution is shown in Fig. 11 and can be compared with Fig. 9. The increase in the intensity of the corona as it approaches the boundary of the shadow turns out to be more gentle for the Schwarzschild BH. This fact can also be used in observations in order to distinguish a BH from a WH.

Fig. 11.

The distribution of the radiation intensity in the equatorial section of the shadow of the Schwarzschild black hole.

4 CONCLUSIONS

Although the physical properties of the WH and BH metrics differ sharply from each other (there is no gravitation in the WH metric at all), the lensing of light rays and the shape of the shadow they create is similar to each other, differing mainly in numerical parameters. These differences are, nevertheless, essential for future attempts to detect WHs in astrophysics.

As noted in Section 1, we will consider more complex models of the WH and screens in future works.

APPENDIX

1.1 EQUATIONS OF PHOTON MOTION

The metric of the WH can be written in the form:

$$d{{s}^{2}} = d{{t}^{2}} - d{{R}^{2}} - ({{R}^{2}} + {{q}^{2}})(d{{\vartheta }^{2}} + {{\sin}^{2}}\vartheta d{{\varphi }^{2}})$$

(3)

or

$$d{{s}^{2}} = d{{t}^{2}} - \frac{{{{r}^{2}}}}{{{{r}^{2}} - {{q}^{2}}}}d{{r}^{2}} - {{r}^{2}}(d{{\vartheta }^{2}} + {{\sin}^{2}}\vartheta d{{\varphi }^{2}}),$$

(4)

where

$${{r}^{2}}(R) = {{R}^{2}} + {{q}^{2}},$$

(5)

$q$ is the size of WH throat, and the radial coordinate $r$ is chosen so that the circumference is $2\pi r$.

Hamilton–Jacobi equation

$${{g}^{{ik}}}\frac{{\partial S}}{{\partial {{x}^{i}}}}\frac{{\partial S}}{{\partial {{x}^{k}}}} - {{m}^{2}} = 0,$$

(6)

for the wormhole metric can be written as:

$$\begin{gathered} \mathop {\left( {\frac{{\partial S}}{{\partial t}}} \right)}\nolimits^2 - \frac{{{{r}^{2}} - {{q}^{2}}}}{{{{r}^{2}}}}\mathop {\left( {\frac{{\partial S}}{{\partial r}}} \right)}\nolimits^2 - \frac{1}{{{{r}^{2}}}}\mathop {\left( {\frac{{\partial S}}{{\partial \vartheta }}} \right)}\nolimits^2 \\ \, - \frac{1}{{{{r}^{2}}{{\sin}^{2}}\vartheta }}\mathop {\left( {\frac{{\partial S}}{{\partial \varphi }}} \right)}\nolimits^2 - {{m}^{2}} = 0. \\ \end{gathered} $$

(7)

By analogy with the Schwarzschild metric, the solution is sought in the form:

$$S = - Et + L\varphi + {{S}_{r}}(r) + {{S}_{\theta }}(\theta ),$$

(8)

since the coordinates $t$ and φ are cyclic, i.e., are not explicitly included in the metric tensor and the Hamilton–Jacobi equation. In the equation (7), the variables can be separated and we get the equations of motion:

$$\frac{{dt}}{{d\lambda }} = E{{r}^{2}},$$

(9)

$$\begin{gathered} \mathop {\left( {\frac{{dr}}{{d\lambda }}} \right)}\nolimits^2 = ({{E}^{2}} - {{m}^{2}}){{r}^{4}} - ({{q}^{2}}({{E}^{2}} - {{m}^{2}}) \\ + \;Q + {{L}^{2}}){{r}^{2}} + {{q}^{2}}(Q + {{L}^{2}}), \\ \end{gathered} $$

(10)

$$\mathop {\left( {\frac{{d\theta }}{{d\lambda }}} \right)}\nolimits^2 = Q - \frac{{{{L}^{2}}{{\cos}^{2}}\theta }}{{{{\sin}^{2}}\theta }},$$

(11)

$$\frac{{d\varphi }}{{d\lambda }} = \frac{L}{{{{\sin}^{2}}\theta }},$$

(12)

where the Carter separation constant $K$ according to [27] is written in the form: $K = Q + {{L}^{2}}$, which differs from its recording in [18]. The equations of motion for a quantum are obtained by putting $m = 0$ in the sys-tem (9)–(12). However, in this case, the equations of motion do not depend on three constants: $E$, $L$, and $Q$, but on two Chandrasekhar constants: $\xi = Q{\text{/}}({{q}^{2}}{{E}^{2}})$ and $\eta = L{\text{/}}qE$. In addition, the equations (10), (11) contain a square root function, which is inconvenient for serial computations. For the convenience of computations, each of these equations can be replaced by two equations, thereby increasing the order of the system [28, 29]. Finally, the system of equations for the motion of a quantum in the WH metric can be written as:

$$\frac{{dt}}{{d\sigma }} = \frac{1}{{{{r}^{2}}}},$$

(13)

$$\frac{{dr}}{{d\sigma }} = {{r}_{1}},$$

(14)

$$\frac{{d{{r}_{1}}}}{{d\sigma }} = 2(\eta - {{\xi }^{2}}){{r}^{3}} - (1 + \eta + {{\xi }^{2}})r,$$

(15)

$$\frac{{d\theta }}{{d\sigma }} = {{\theta }_{1}},$$

(16)

$$\frac{{d{{\theta }_{1}}}}{{d\sigma }} = \frac{{{{\xi }^{2}}\cos\theta }}{{{{\sin}^{3}}{\kern 1pt} \theta }},$$

(17)

$$\frac{{d\varphi }}{{d\sigma }} = \frac{\xi }{{{{\sin}^{2}}{\kern 1pt} \theta }}.$$

(18)

To set the initial values, assume that the observer is at a point with coordinates $(r,\theta ,\varphi ) = ({{r}_{0}},{{\theta }_{0}},0)$ (i.e., in the plane $xz$ in Cartesian coordinates) and launches a quantum at the direction of the WH to the point with coordinates $A({{b}_{y}},{{b}_{z}})$ in the plane of the sky and the impact parameter $b = \sqrt {b_{y}^{2} + b_{z}^{2}}$. The geometrical location of this point is illustrated in Fig. 12. Then, the Chandrasekhar constants can be expressed explicitly through the coordinates of the observer and the impact parameter:

$$\xi = \frac{{{{r}_{0}}{{b}_{y}}\sin{{\theta }_{0}}}}{{\sqrt {r_{0}^{2} + b_{y}^{2} + b_{z}^{2}} }},\quad \eta = \frac{{r_{0}^{2}(b_{z}^{2} + b_{y}^{2}{{\cos}^{2}}{{\theta }_{0}})}}{{r_{0}^{2} + b_{y}^{2} + b_{z}^{2}}}.$$

(19)

All linear dimensions in the formulas (19) are normalized to the radius of the WH throat, i.e., in Fig. 12${{b}_{y}} \approx 2$, ${{b}_{z}} \approx 1.5$.

Fig. 12.

Impact parameter for a quantum directed towards a wormhole.

For the Schwarzschild metric, a similar system of equations is written as:

$$\frac{{dt}}{{d\sigma }} = \frac{1}{{{{r}^{2}}(1 - 2r)}},$$

$$\frac{{dr}}{{d\sigma }} = {{r}_{1}},$$

(21)

$$\frac{{d{{r}_{1}}}}{{d\sigma }} = 3(\eta + {{\xi }^{2}}){{r}^{2}} - (\eta + {{\xi }^{2}})r = (\eta + {{\xi }^{2}})(3r - 1)r,$$

$$\frac{{d\theta }}{{d\sigma }} = {{\theta }_{1}},$$

(23)

$$\frac{{d{{\theta }_{1}}}}{{d\sigma }} = \frac{{{{\xi }^{2}}\cos\theta }}{{{{\sin}^{3}}{\kern 1pt} \theta }},$$

(24)

$$\frac{{d\varphi }}{{d\sigma }} = \frac{\xi }{{{{\sin}^{2}}{\kern 1pt} \theta }},$$

(25)

and the Chandrasekhar constants

$$\begin{gathered} \xi = \frac{{r_{0}^{{3/2}}{{b}_{y}}\sin{{\theta }_{0}}}}{{\sqrt {({{r}_{0}} - 2)(r_{0}^{2} + b_{y}^{2} + b_{z}^{2})} }}, \\ \eta = \frac{{r_{0}^{3}(b_{z}^{2} + b_{y}^{2}{{\cos}^{2}}{{\theta }_{0}})}}{{({{r}_{0}} - 2)(r_{0}^{2} + b_{y}^{2} + b_{z}^{2})}}. \\ \end{gathered} $$

(26)

For the numerical solution of the ordinary differential equations, there are many software packages that are freely distributed on the Internet. The calculations were performed with a relative accuracy $\delta = {{10}^{{ - 7}}}$ and were verified using the first integrals of the systems (13)–(18) and (20)–(25) [28, 29].