1 INTRODUCTION

The study of the periods of eclipsing binaries is a convenient tool for examining the processes that occur in close binary systems. Secular variations in the period (monotonic increase or decrease) are associated with the processes of exchange of matter between the components and the loss of matter by the system as a whole [1–3]. Quantitative estimates of the decrease (or increase) rate of the period can help to choose among the available theoretical models. Cyclic variations in the orbital period of close binary systems can be caused by the rotation of the apse line (in an eccentric orbit) or by the presence of a third body (or multiple additional bodies) in the system. However, the light-time effect is not always suitable for explaining cyclic variations in the orbital period due to unacceptable parameters of the third body or data that contradict the hypothesis of motion in a long-period orbit. At present, the studies of the cyclic variations in the periods of eclipsing binaries increasingly more often consider the influence of magnetic cycles when it comes to systems with components of late spectral types with a convective shell. Quite often, the variations in the orbital period are a superposition of multiple variations of different nature.

For the eclipsing binary systems considered in this paper, the time dependences of the differences between the observed times of minima and those calculated with linear elements have a rather complex appearance. The shape of all the diagrams indicates a secular decrease in the period, while the corresponding inverse parabola is distorted by additional variations; although the presence of an inverse parabola was obvious to all researchers of these systems, the additional variations in the period were difficult to interpret.

2 TIME VARIATIONS IN THE ORBITAL PERIOD OF XZ Per

The studies of the star XZ Per (HV 03553, GSC 3328.03186, Vmax = 11.4m, P = 1.15163d) began with the visual observations by Dubyago and Martynov, in which the visual light curve was constructed [4]. Lavrov [5] obtained the photometric elements of the XZ Per orbit by solving this light curve. Using the same visual observations and supplementing them with his later data, Tsesevich [6, 7] studied the behavior of the XZ Per’s period and found that it varied smoothly. The spectral class of the main component, F2-5, was determined by Popper [8]. There is no radial-velocity curve for this system. In [9], a detailed photometric study of XZ Per was performed. Photometric orbital elements were obtained from CCD observations in several spectral bands, and the absolute characteristics of the constituent stars were determined. Variations in the period of XZ Per were studied by many authors, but a fairly large number of the times of minima were considered in [9, 10]. In both of these studies, the variations in the XZ Per period were represented as a superposition of the secular decrease in the period and its jumps. A similar interpretation of the variations in the orbital period was proposed at one time for the eclipsing binary systems RW Tau, TU Her, and TY Peg; however, later it was shown that these variations can be represented by smooth curves corresponding to the light-time effect or magnetic oscillations [11, 12].

To study the variations in the period of the eclipsing binary system XZ Per, we used the times of minima from the B. R. N. O. database [13] and the times of minima from [9] not included in this database. In total, there are 498 times of the main minimum: 414 visual, 9 photographic, 75 from the photoelectric and CCD observations, as well as 3 times of the secondary minimum. Figure 1 shows the deviations (O – C)1 of the observed (O) times of minima of XZ Per from those calculated (C) with linear elements obtained by the least squares method using all the available times of the main minimum:

$$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2\,443\,507.4630(8) \\ + \;1.15163143{{(11)}^{{\text{d}}}}T, \\ \end{gathered} $$
(1)

where T is the observation epoch. Photoelectric and CCD observations in this figure are indicated by large dots, visual observations by small dots, and photographic observations by triangles. Further analysis did not include three visual points that greatly deviate from the general trend: JD = 2 444 267.538, 2 444 881.358, 2 447 001.557. Previous authors who studied the variations in the XZ Per period [9, 10] represented them, first of all, as a parabola. We also represented the variations in the XZ Per period as a quadratic dependence:

$$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2\,443\,507.4746(6) \\ + \;1.15163079{{(7)}^{{\text{d}}}}T-2.17{{(7)}^{{\text{d}}}} \times {{10}^{{-10}}}{{T}^{2}}. \\ \end{gathered} $$
(2)
Fig. 1.
figure 1

Deviations (O – C)1 of the observed minima times of XZ Per from those calculated with linear elements (1). The photographic observations are indicated by triangles, visual observations by small dots, photoelectric and CCD observations by large dots.

Full size image

In [9], the variations in the XZ Per period were studied using almost the same times of minima (except for the most recent ones). The author represented the residual differences obtained after eliminating the parabola as jumps of the period (the same was done in [10]). However, it is quite possible to represent them as a smoothed curve, and “spikes” could appear due to the presence of a second wave with a shorter period. For this reason, we represented the variations in the orbital period of XZ Per as a superposition of a parabola and a light-time effect [14]:

$$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2\,443\,507.4761(9) \\ + \;1.15163140{{(4)}^{{\text{d}}}}T-1.01{{(6)}^{{\text{d}}}} \times {{10}^{{-10}}}{{T}^{2}} \\ + \;\frac{{{{a}_{3}}\sin {{i}_{3}}}}{c}(1-{{e}_{3}}\cos E)\sin ({v} + {{\omega }_{3}}). \\ \end{gathered} $$
(3)

The expression for the light-time effect uses the following notations for the orbital elements of the eclipsing binary system with respect to the center of gravity of the triple system: а3 is the semimajor axis; i3 is the inclination; е3 is the eccentricity; ω3 is the longitude of periastron; \({v}\) and Е are the true and eccentric anomalies, respectively, which are measured in the same orbit; and c is the speed of light. The initial values of the parameters of the long-period orbit were found by enumeration in the range of their possible values. They were further refined using the method of differential corrections [15] together with the linear elements and the quadratic term. At the same time, the errors in determining the parameters were calculated. The final values of the parameters of the long-period orbit are given in Table 1. The following notation is used in the table: P3 is the period of revolution in a long-period orbit, JD3 is the time of passage through the periastron, and A3 = (\({{a}_{3}}\sin {{i}_{3}}\))/с. The time dependence of the residuals (O – C)3 obtained by subtracting the theoretical parabola with the parameters from representation (3) from the observed times of minima is given in Fig. 2. The theoretical curve for the light–time effect with the obtained parameters is drawn as a solid line.

Table 1.   Parameters of the hypothetical light-time effect in the variations of the orbital period of XZ Per for the quadratic representation of the times of minima
Full size table
Fig. 2.
figure 2

Time dependence of the (O – C)2 values obtained by subtracting the theoretical parabola (3) from the observed minima times of XZ Per. The solid curve shows the theoretical curve for the light-time effect with the parameters from Table 1.

Full size image

The residuals after subtracting the theoretical times of minima calculated by formula (3) from the observed times of minima are shown in the upper part of Fig. 5. The positions of the photographic and visual points in this graph are rather random, but some “surges” can be seen. The data obtained from the photoelectric and CCD observations show distinct variations. It was not possible to construct a theoretical curve that would represent all the data in this graph. For this reason, a different approach was tried to interpret the variations in the XZ Per period. They were represented directly by the light-time effect. Since the time dependence of the residuals after subtraction of the theoretical curve from the observations for the light-time effect also exhibits fluctuations, the variations in the XZ Per period were represented by a superposition of two light-time effects:

$$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2\,443\,507.4652(1) \\ + \;1.15163121{{(1)}^{{\text{d}}}}T + LTE1 + LTE2. \\ \end{gathered} $$
(4)

The parameters of these light-time effects were determined using the method of successive approximations described in detail in [16]. At each step, the parameters of the light-time effects were determined by enumeration in the range of their possible values. At the same time, the linear elements for the wave with a longer period were refined. The parameters of the wave with a shorter period were determined with fixed linear elements. The final parameters of the light-time effect for each wave were refined using the method of differential corrections with fixed linear elements. At the same time, the errors in determining the parameters were calculated. These parameters are given in Table 2, where the parameters with subscript G refer to the orbit with a longer period, and those with subscript L refer to the orbit with a shorter period. Since the linear elements were determined only by enumeration, the size of the enumeration step is indicated for them in parentheses.

Table 2.   Parameters of the hypothetical light-time effects in the variations of the orbital period of XZ Per for the linear representation of the times of minima
Full size table

Figure 3 shows the time variations in the differences obtained by subtracting the theoretical curve for the wave with a shorter period from the deviations of the observed minima times of XZ Per from those calculated with linear elements (4). The solid line in this figure is the theoretical curve for the wave with a larger period with parameters from Table 2. Figure 4 shows the time variations in the differences obtained by subtracting the theoretical curve for the wave with a larger period from the deviations of the observed times minima of XZ Per from those calculated with linear elements (4). The solid line in this figure is the theoretical curve for the wave with a shorter period with the parameters from Table 2.

Fig. 3.
figure 3

Time variations in the differences obtained by subtracting the theoretical curve for the wave with a shorter period from the deviations of the observed minima times of XZ Per from those calculated with the linear elements (4). The solid line is the theoretical curve for the wave with a larger period with the parameters from Table 2. The notations are the same as in Fig. 1.

Full size image
Fig. 4.
figure 4

Time variations in the differences obtained by subtracting the theoretical curve for the wave with a greater period from the deviations of the observed minima times of XZ Per from those calculated with the linear elements (4). The solid line is the theoretical curve for the wave with a shorter period with the parameters from Table 2. The notations are the same as in Fig. 1.

Full size image
Fig. 5.
figure 5

Residuals after subtracting (a) the parabola and the light-time effect according to formula (3) and (b) two light-time effects according to formula (4) from the observed times of minima. The solid lines are the theoretical curves for the light-time effects obtained from the photoelectric and CCD observations. The notations are the same as in Fig. 1.

Full size image

The residuals after subtracting the theoretical times of minima calculated by formula (4) from the observed ones are shown in the lower part of Fig. 5. This graph is almost the same as that obtained for the quadratic representation. For example, it is possible to represent the variations in the XZ Per period either as a superposition of a parabola and a light-time effect, or as a sum of two light-time effects; the resulting picture is almost the same. The solid lines in this figure are the theoretical curves for the light-time effects obtained from photoelectric and CCD observations: for the first case, the period is 13 years, and the amplitude is 0.0059 days; for the second case, the period is 12 years, and the amplitude is 0.0055 days. Unfortunately, in either of the two cases, these curves do not reflect visual observations. Further high-precision observations are required to clarify the character of these residual variations in the period.

3 POSSIBLE CAUSES OF VARIATIONS IN THE ORBITAL PERIOD OF XZ Per

The rate of a secular decrease in the period is calculated by the formula: dP/dt = 2Q/P, where Q is the coefficient of the quadratic term in the representation of the times of minima. For XZ Per, we obtained Q = –1.01(6)d × 10–10, from which dP/dt = –6.41 × 10–8 days/year. A secular decrease in the period can be caused by the system’s loss of the angular momentum; the most effective mechanism for the loss of the angular momentum is magnetic braking [17–19].

The obtained parameters of long-period orbits allow us to calculate the mass function for each light-time effect under the assumption that there is only one additional body in the system:

$$f({{M}_{3}}) = \frac{{a_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{P_{3}^{2}}} = \frac{{M_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}})}}^{2}}}}.$$
(5)

Here, the masses are expressed in the solar masses, the semimajor axes of the orbits are in astronomical units, and the periods are in years; M1 and M2 are the masses of the components of the eclipsing binary system, and M3 is the mass of the additional component. The values of the minimum mass of the third body for each additional orbit were obtained with the component masses of the eclipsing binary system from [9]: M1 = 1.41\({{M}_{ \odot }}\), M2 = 0.91\({{M}_{ \odot }}\). These values are given in Table 1 for the quadratic representation and in Table 2 for the linear representation of the times of minima.

In the case of quadratic elements, only one additional body is assumed. In the case of linear elements, there can be different options: (1) one of the cyclic variations in the period is caused by the presence of the third body, while the second variation (or both) is due to other reasons (see below); (2) both cyclic variations in the period are caused by the light-time effects. In this case, we have a quadruple system. For a hierarchical quadruple system, the mass function is related to the masses of the components by the following expression:

$$f({{M}_{4}}) = \frac{{a_{4}^{3}{{{\sin }}^{3}}{{i}_{4}}}}{{P_{4}^{2}}} = \frac{{M_{4}^{3}{{{\sin }}^{3}}{{i}_{4}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}} + {{M}_{4}})}}^{2}}}}.$$
(6)

Here, subscript 3 refers to an orbit with a shorter period, and subscript 4 refers to an orbit with a longer period, respectively. In this case, the minimum mass of the most distant body \({{M}_{4}}\sin {{i}_{4}}\) = 0.405\({{M}_{ \odot }}\).

In all these cases, the minimum mass of additional components turns out to be small. The actual mass of the probable additional bodies cannot be known until the inclinations of their orbits are known. It would be useful to attempt to find the fraction of the third light in the total brightness of the system. In the solution of the light curve in [9], the problem of determining the fraction of the third light in the system was not posed, since the author did not assume the presence of a third body in the system.

As an alternative to the third body hypothesis, one can assume that the observed cyclic variations in the period are a manifestation of magnetic activity. The secondary component in the eclipsing binary system XZ Per has the spectral type K4 [9] and should have a convective shell. A model was proposed in [20] in which gravitational quadrupole interaction provides a mechanism by which the orbit reacts to changes in the internal structure of an active star. In this model, the modulation amplitude of the orbital period ΔP and the amplitude of the oscillations Δ(О – С) in the О–С diagram are related by the ratio ΔP/P0 = 2π Δ(О – С)/Pmod. Taking the radii and masses of the components according to [9], we find the semimajor axis of the binary system’s relative orbit from Kepler’s third law: a = 6.12\({{R}_{ \odot }}\). Furthermore, using the sequence of formulas given in [20], we find the estimates of the angular momentum ΔJ transferred from the star’s core to its shell and vice versa, the amount of energy ΔE required to transfer the angular momentum to the star’s outer part, the magnetic field strength B of the active component, and variations in its luminosity ΔL. These values are given in Table 3 for each modulating period.

Table 3.   Values characterizing the magnetic activity cycles of the secondary component of the eclipsing binary system XZ Per
Full size table

The obtained estimates of the magnetic and energy values for all modulating periods are well within the acceptable range. Possible fluctuations in the luminosity of the secondary component are small. Therefore, magnetic oscillations can be the cause of cyclic variations in the orbital period of XZ Per.

4 TIME VARIATIONS IN THE ORBITAL PERIOD OF BO Vul

The star BO Vul (HD 187949, Vmax = 10.5m, P = 1.9458d) was discovered by Hoffmeister [21] from photographic observations as an Algol-type eclipsing variable. The first ephemerides were determined in [22] from visual observations. Two photographic light curves were plotted in [23, 24]. Szafraniec [25] plotted the light curve of BO Vul at the major minimum from visual observations. However, the photometric orbital elements were determined only from the photographic light curve [23], and the spectral types of the components in the same study were estimated as F2 + K3. For this system, there is neither a radial velocity curve, nor modern high-precision observations of the light curve. Only approximate values of the absolute characteristics of the components are available [26].

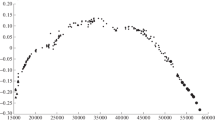
The fact that the period of the system is variable was first noticed by Ahnert [27], who found two sets of ephemerides for two ranges of Julian days and stated that it was impossible to derive average ephemeris. Baldwin [28] noted that there were several orbital period changes in BO Vul. The first detailed analysis of the variations in the orbital period of this system was carried out in [29]. The authors represented the variations in the orbital period of BO Vul as a superposition of a secular decrease and sudden jumps. They suggested that the secular variation could be caused by the stellar magnetic wind, while the sudden jumps may be due to the instability of the accretion disk around the main star. Erdem [30] examined the variations in the orbital period of BO Vul on the basis of a large number of times of minima, mainly visual ones, and represented them as a superposition of the secular decrease in the period and the light-time effect. Zasche [31] studied the same times of minima using also photographic data and obtained a result that is almost the same as the one obtained in [30]. Since then, quite a lot of times of minima have been obtained from photoelectric and CCD observations. Figure 6 shows the deviations (O – C) of the observed (O) times of minima of BO Vul from those calculated (C) with quadratic elements from [30]. The solid line in this figure is the theoretical curve for the light-time effect calculated with the parameters from the same study. It can be seen from this figure that the results from [30] are in good agreement with early observations, but do not agree at all with the latest photoelectric and CCD observations. The situation is the same if we use the results from [31]. Based on the new data, the variations in the BO Vul period should be revised.

Fig. 6.
figure 6

Deviations (O – C) of the observed (О) minima times of BO Vul from those calculated (C) with the quadratic elements from [30]. The solid line is the theoretical curve for the light-time effect calculated with the parameters from the same study. The visual observations are indicated by small dots, photoelectric and CCD observations by large dots.

Full size image

To study the variations in the period of the eclipsing binary system BO Vul, we used the times of the main minimum from the B. R. N. O. database [13]. In total, there are 359 times of the main minimum: 260 visual, 67 photographic, and 32 from the photoelectric and CCD observations, as well as 1 time of the secondary minimum. Figure 7 shows the deviations (O – C)1 of the observed (О) times of minima of BO Vul from those calculated (C) with linear elements obtained by the least squares method using all the available times of the main minimum:

$$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2\,435\,989.436(2) \\ + \;1.9458690{{(4)}^{{\text{d}}}}T, \\ \end{gathered} $$
(7)

where T is the observation epoch. In this figure, photoelectric and CCD observations are indicated by large dots, visual observations by small dots, and photographic observations by triangles. The photographic data and the very first visual point were not used in the analysis of the variations in the BO Vul period. The remaining times of minima were represented by a quadratic dependence, the parameters of which were also found using the least squares method:

$$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2\,435\,989.416(2) \\ + \;1.9458795{{(9)}^{{\text{d}}}}T-10.0{{(8)}^{{\text{d}}}} \times {{10}^{{-10}}}{{T}^{2}}. \\ \end{gathered} $$
(8)
Fig. 7.
figure 7

Deviations (O – C)1 of the observed minima times of BO Vul from those calculated with linear elements (7). The photographic observations are indicated by triangles, visual observations by small dots, photoelectric and CCD observations by large dots.

Full size image

Figure 8 shows the deviations (O – C)2 of the observed minima times of BO Vul from those calculated with linear elements from representation (8). The theoretical parabola with the parameters from the same representation is shown by the solid curve. The residual differences obtained after excluding the parabola are shown in Fig. 9.

Fig. 8.
figure 8

Deviations (O – C)2 of the observed minima times of BO Vul from those calculated with linear elements from representation (8). The theoretical parabola with the parameters from the same representation is shown with the solid curve. The notations are the same as in Fig. 6.

Full size image
Fig. 9.
figure 9

Time dependence of the residuals (O – C)3 obtained by subtracting the theoretical parabola from the observed minima times of BO Vul. The solid line is the theoretical curve for the light-time effect with the parameters from Table 4. Below is the time dependence of the (O – C)4 values obtained by subtracting the theoretical times of minima calculated with quadratic elements and the light-time effect with the parameters from Table 4 from the observed times of minima. The notations are the same as in Fig. 6.

Full size image

Assuming that the cyclic variations in the period are caused by the presence of a third body in the system, we can express them in terms of the parameters of a long-period orbit by means of the light-time effect. The parameters of the long-period orbit of BO Vul were determined in the same way as for XZ Per. At the same time, the quadratic elements were also refined. In the calculations, the visual data were assigned a weight of 1, and the photoelectric and CCD observations were assigned a weight of 10. Table 4 shows the values we obtained for the parameters of the light-time effect and quadratic elements: the orbital period of the binary system P2, the initial epoch JD2, and the coefficient of the quadratic term Q. The solid line in Fig. 9 is the theoretical curve for the light-time effect with the parameters from Table 4. At the bottom of Fig. 9 are the residuals after subtracting the parabola and the light-time effect with the parameters from Table 4 from the observed times of minima. The figure shows that the theoretical curve for the light-time effect adequately fits the observations for which JD > 2 445 000, but does not pass well among the earlier points. In [30], points with JD < 2 452 000 were considered, and the obtained theoretical curve passed well over all such points; however, as shown in Fig. 6, the representation obtained in that study is completely inconsistent with later data. There can be two causes for this discrepancy: (1) the light-time effect is indeed observed in the system, but the theoretical curve that involves the photoelectric and CCD data does not agree well with early observations due to the low accuracy of old visual observations; (2) the cyclic variations in the period are caused not by the light-time effect, but by other reasons, for example, magnetic oscillations, in which case the oscillations do not follow a strict curve.

Table 4.   Parameters of the hypothetical long-period orbit of BO Vul
Full size table

5 POSSIBLE CAUSES OF VARIATIONS IN THE ORBITAL PERIOD OF BO Vul

If the cyclic oscillations of the BO Vul period represent the light-time effect, using the parameters of the long-period orbit that we found (Table 4), we can calculate the mass function of the triple system: f(M3) = 0.068 \({{M}_{ \odot }}\). Using the masses of the components of the eclipsing binary system from [26] М1 = 1.45 \({{M}_{ \odot }}\), М2 = 0.64 \({{M}_{ \odot }}\), we obtain \({{M}_{3}}\sin {{i}_{3}}\) = 0.83 \({{M}_{ \odot }}\). Assuming the third component is a main sequence star, from the mass–luminosity ratio in the corresponding mass range [32], we find the luminosity of the third body: L3 = 0.38 \({{L}_{ \odot }}\). The luminosities of the components of an eclipsing binary system are determined based on the estimates of the mass and relative luminosity of the main component given in [26]. The main component of the eclipsing binary system is a main-sequence star, and its luminosity can be found from the mass–luminosity ratio in the corresponding mass range [32]: L1 = 4.97 \({{L}_{ \odot }}\). According to [26], its relative luminosity is 0.81; the absolute luminosity of the secondary component is then L2 = 1.16 \({{L}_{ \odot }}\). Now, we can find the relative luminosity of the supposed third body: L3/(L1 + L2 + L3) = 0.06. This amount of third light could be found from the solution of the light curve. The presence of a third body in this system cannot be ruled out, especially since there is neither an exact light curve, nor a radial-velocity curve, so there are only approximate estimates for the absolute characteristics of the components.

The secondary component in the eclipsing binary system BO Vul has spectral type G0 IV [26] and must have a convective shell; therefore, the observed cyclic changes in the period may be a manifestation of magnetic activity. For the above estimates of the component masses, we find the semimajor axis of the binary system’s relative orbit from Kepler’s third law: a = 8.38 \({{R}_{ \odot }}\). The secondary component radius is taken from the catalog [26]: R2 = 2.55 \({{R}_{ \odot }}\). Furthermore, using the same formulas and notation as in the previous section, we find estimates of the values that characterize magnetic cycles. They are given in Table 5. It can be seen from the table that magnetic oscillations can be the cause of cyclic variations in the period of BO Vul.

Table 5.   Values characterizing the magnetic activity cycles of the secondary component of the eclipsing binary system BO Vul
Full size table

The inverse parabola in the time dependence of the deviations of the observed times of minima from those calculated with linear elements indicates a secular decrease in the period. For BO Vul, Q = –1.19 × 10–9 and dP/dt = –4.47 × 10–7 days/year. A decrease in the period can be caused by the system’s loss of angular momentum due to magnetic braking.

6 CONCLUSIONS

The variations in the orbital period of the eclipsing binary system XZ Per are equally well represented as a superposition of the secular decrease and cyclic variations, and as a sum of two cyclic variations. In the first case, the monotonic component can be a consequence of the loss of angular momentum by the system due to magnetic braking. The cyclic variations in the period can occur due to the presence of a third body in the system or due to the magnetic activity of the secondary component with a convective shell. In the second case, it is possible to assume the presence of two additional bodies in the system, or to attribute one of the period oscillations to the light-time effect, and the other to the magnetic activity of the secondary component. In both cases, after excluding the corresponding theoretical curves from the observed times of minima, almost identical oscillations of the period remain, the nature of which is not yet clear. To clarify the nature of these oscillations, further high-precision observations of the times of minima are required.

The variations in the orbital period of the eclipsing binary system BO Vul can be represented as a superposition of an inverse parabola and cyclic variations. The observed cyclic variations in the period can occur due to the presence of a third body in the system or due to the magnetic activity of the secondary component with a convective shell. For this system, there are very few high-precision photoelectric and CCD observations of the times of minima; the bulk of the observations is visual. The theoretical curve for the light-time effect obtained from the residuals after excluding the parabola adequately fits the observations for JD > 2 446 000, while the discrepancy between the theory and the earlier observations is quite noticeable. The results of previous authors, on the contrary, closely agree with the early observations, but are inconsistent with the photoelectric and CCD observations. It is possible that these oscillations cannot be represented by a regular curve; in this case, they should be attributed to magnetic activity. Additional period oscillations are also possible. Only further observations will help to resolve this question.