APPENDIX A
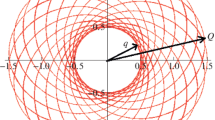
From the spherical triangle in Fig. 1, we obtain the formulas
$$\sin \left( {\Delta {{{\bar {\omega }}}_{1}}} \right) = \frac{{\sin i_{2}^{'}\sin \left( {\Delta \Omega '} \right)}}{{\sin \left( {\Delta i} \right)}},$$
$$\cos \left( {\Delta {{{\bar {\omega }}}_{1}}} \right) = \frac{{ - \sin i_{1}^{'}\cos i_{2}^{'} + \cos i_{1}^{'}\sin i_{2}^{'}\cos \left( {\Delta \Omega '} \right)}}{{\sin \left( {\Delta i} \right)}},$$
$$\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) = \frac{{\sin i_{1}^{'}\sin \left( {\Delta \Omega '} \right)}}{{\sin \left( {\Delta i} \right)}},$$
(A1)
$$\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) = \frac{{\sin i_{2}^{'}\cos i_{1}^{'} - \cos i_{2}^{'}\sin i_{1}^{'}\cos \left( {\Delta \Omega '} \right)}}{{\sin \left( {\Delta i} \right)}}.$$
The components of the vector of the moment of forces (divided by the absolute value of the angular momentum of the second ring) acting from the first ring on the second are then transformed as
$$\frac{{M_{{\xi '}}^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}} = \frac{{M_{\xi }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) - \frac{{M_{\eta }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right),$$
$$\frac{{M_{{\eta '}}^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}} = \frac{{M_{\xi }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) + \frac{{M_{\eta }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right),$$
(A2)
$$\frac{{M_{{\zeta '}}^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}} = \frac{{M_{\zeta }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}.$$
COEFFICIENTS \(i_{{kl}}^{{\left( 2 \right)}}\), \({\bar {v}}_{{klm}}^{{\left( 2 \right)}}\), AND \(\Omega _{{klm}}^{{\left( 2 \right)}}\)
IN THE RIGHT-HAND PARTS
OF EQS. (39)
We provide the exact expressions for the remaining sixteen coefficients:
$$\begin{gathered} i_{{20}}^{{(2)}}\, = \,\left( {\frac{{1\, - \,3{{n}^{2}}\, + \,23{{n}^{4}}{\kern 1pt} + \,3{{n}^{6}}}}{{{{{(1 - n)}}^{2}}}}{\kern 1pt} E(k)\, - \,(1\, - \,{{n}^{2}}\, + \,3{{n}^{4}})K(k)} \right) \\ \times \;2n\sin {{\omega }_{1}}\cos {{\omega }_{1}}; \\ \end{gathered} $$
(B1)
$$\begin{gathered} i_{{02}}^{{(2)}}\, = \,\left( {\frac{{3\, + \,23{{n}^{2}}\, - \,3{{n}^{4}}{\kern 1pt} + \,{{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}{\kern 1pt} E(k)\, - \,(3\, - \,{{n}^{2}}\, + \,{{n}^{4}})K(k)} \right) \\ \times \;2n\sin {{\omega }_{2}}\cos {{\omega }_{2}}; \\ \end{gathered} $$
(B2)
$$\begin{gathered} i_{{11}}^{{\left( 2 \right)}} = \left( {\left( {\frac{{4 - 15{{n}^{2}} - 26{{n}^{4}} - 15{{n}^{6}} + 4{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right.} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(4\, - \,11{{n}^{2}}\, + \,4{{n}^{4}})(1\, + \,{{n}^{2}})K(k)} \right){\kern 1pt} \cos {{\omega }_{1}}\sin {{\omega }_{2}} \\ - \;\left( {\frac{{4 - 9{{n}^{2}} + 58{{n}^{4}} - 9{{n}^{6}} + 4{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {\left. {^{{^{{^{{^{{}}}}}}}} - \;(4\, - \,5{{n}^{2}}\, + \,4{{n}^{4}})(1\, + \,{{n}^{2}})K(k)} \right)\sin {{\omega }_{1}}\cos {{\omega }_{2}}} \right){\kern 1pt} ; \\ \end{gathered} $$
(B3)
$${\bar {v}}_{{102}}^{{\left( 2 \right)}} = \left( {\frac{{4 - 15{{n}^{2}} - 26{{n}^{4}} - 15{{n}^{6}} + 4{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right.$$
$$\left. {^{{^{{^{{^{{}}}}}}}} - \;(4 - 11{{n}^{2}} + 4{{n}^{4}})(1 + {{n}^{2}})K(k)} \right)$$
$$ \times \;\cos {{\omega }_{1}}\cos {{\omega }_{2}} + \sin {{\omega }_{1}}\sin {{\omega }_{2}}$$
(B4)
$$ \times \;\left( {\frac{{4 - 21{{n}^{2}} - 110{{n}^{4}} - 21{{n}^{6}} + 4{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right.$$
$$\left. {^{{^{{^{{^{{}}}}}}}} - \;(4 - {{n}^{2}})(1 - 4{{n}^{2}})(1 + {{n}^{2}})K(k)} \right);$$
$$\begin{gathered} {\bar {v}}_{{012}}^{{\left( 2 \right)}} = 2n\left( {\frac{{3 + 47{{n}^{2}} + 21{{n}^{4}} + {{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(3 + 5{{n}^{2}} + {{n}^{4}})K(k)} \right) \\ - \;\left( {\frac{{3 + 23{{n}^{2}} - 3{{n}^{4}} + {{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k) - (3 - {{n}^{2}} + {{n}^{4}})K(k)} \right) \\ \times \;4n{{\cos }^{2}}{\kern 1pt} {{\omega }_{2}}; \\ \end{gathered} $$
(B5)
$$\begin{gathered} {\bar {v}}_{{300}}^{{\left( 2 \right)}} = \left( {\frac{{9 + 50{{n}^{2}} - 15{{n}^{4}} + 4{{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(9 - 7{{n}^{2}} + 4{{n}^{4}})K(k)} \right){{n}^{2}}\cos \left( {{{\omega }_{2}} - {{\omega }_{1}}} \right); \\ \end{gathered} $$
(B6)
$$\begin{gathered} {\bar {v}}_{{210}}^{{\left( 2 \right)}} = 6n\left( {\frac{{(1 + {{n}^{2}})(1 - 4n + {{n}^{2}})(1 + 4n + {{n}^{2}})}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(1 - 5{{n}^{2}} + {{n}^{4}})K(k)} \right) \\ - \;\left( {\frac{{(1 + {{n}^{2}})(1 - 2n - {{n}^{2}})(1 + 2n - {{n}^{2}})}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \,(1\, - \,n\, - \,{{n}^{2}})(1\, + \,n\, - \,{{n}^{2}})K(k)} \right)\, \times \,12n{{\sin }^{2}}({{\omega }_{2}}\, - \,{{\omega }_{1}}); \\ \end{gathered} $$
(B7)
$$\begin{gathered} {\bar {v}}_{{120}}^{{\left( 2 \right)}} = \left( {\frac{{4 - 21{{n}^{2}} + 118{{n}^{4}} + 51{{n}^{6}} - 8{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(1 - 3{{n}^{2}} + 8{{n}^{4}})(4 - {{n}^{2}})K(k)} \right)\cos \left( {{{\omega }_{2}} - {{\omega }_{1}}} \right); \\ \end{gathered} $$
(B8)
$$\begin{gathered} {\bar {v}}_{{100}}^{{\left( 2 \right)}} = \left( {\frac{{1 - {{n}^{2}} + {{n}^{4}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k) - (1 + {{n}^{2}})K(k)} \right) \\ \times \;16{{(1 - {{n}^{2}})}^{2}}\cos \left( {{{\omega }_{2}} - {{\omega }_{1}}} \right); \\ \end{gathered} $$
(B9)
$$\begin{gathered} {\bar {v}}_{{030}}^{{\left( 2 \right)}} = \left( {\frac{{1 + {{n}^{2}} - 25{{n}^{4}} - {{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(1 - 3{{n}^{2}} - {{n}^{4}})K(k)} \right) \times 2n; \\ \end{gathered} $$
(B10)
$${\bar {v}}_{{010}}^{{\left( 2 \right)}} = - \left( {\frac{{1 + {{n}^{2}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k) - K(k)} \right) \times 8n{{(1 - {{n}^{2}})}^{2}};$$
(B11)
other coefficients \({\bar {v}}_{{klm}}^{{\left( 2 \right)}} = 0\);
$$\begin{gathered} \Omega _{{002}}^{{\left( 2 \right)}} = \left( {\frac{{(1 + {{n}^{2}})(1 - 4n + {{n}^{2}})(1 + 4n + {{n}^{2}})}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(1 - 5{{n}^{2}} + {{n}^{4}})K(k)} \right)n; \\ \end{gathered} $$
(B12)
$$\begin{gathered} \Omega _{{200}}^{{\left( 2 \right)}} = \left( {\frac{{1 + 21{{n}^{2}} + 47{{n}^{4}} + 3{{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(1 + 5{{n}^{2}} + 3{{n}^{4}})K(k)} \right)n \\ - \;\left( {\frac{{1 - 3{{n}^{2}} + 23{{n}^{4}} + 3{{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(1 - {{n}^{2}} + 3{{n}^{4}})K(k)} \right) \times 2n{{\cos }^{2}}{\kern 1pt} {{\omega }_{1}}; \\ \end{gathered} $$
(B13)
$$\begin{gathered} \Omega _{{110}}^{{\left( 2 \right)}} = \left( {\frac{{4 - 15{{n}^{2}} - 26{{n}^{4}} - 15{{n}^{6}} + 4{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(4\, - \,11{{n}^{2}}\, + \,4{{n}^{4}})(1\, + \,{{n}^{2}})K(k)} \right)\cos {{\omega }_{1}}\cos {{\omega }_{2}} \\ + \;\left( {\frac{{4 - 21{{n}^{2}} - 110{{n}^{4}} - 21{{n}^{6}} + 4{{n}^{8}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \,(4\, - \,{{n}^{2}})(1\, - \,4{{n}^{2}})(1\, + \,{{n}^{2}})K(k)} \right)\sin {{\omega }_{1}}\sin {{\omega }_{2}}{\kern 1pt} ; \\ \end{gathered} $$
(B14)
$$\begin{gathered} \Omega _{{020}}^{{\left( 2 \right)}} = \left( {\frac{{5 + 45{{n}^{2}} + 19{{n}^{4}} + 3{{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k)} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \;(5 + {{n}^{2}} + 3{{n}^{4}})K(k)} \right)n \\ - \;\left( {\frac{{3\, + \,23{{n}^{2}}\, - \,3{{n}^{4}}\, + \,{{n}^{6}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}{\kern 1pt} E(k)\, - \,(3\, - \,{{n}^{2}}\, + \,{{n}^{4}})K(k)} \right) \\ \times \;2n{{\cos }^{2}}{{\omega }_{2}}; \\ \end{gathered} $$
(B15)
$$\Omega _{{000}}^{{\left( 2 \right)}} = \left( {\frac{{1 + {{n}^{2}}}}{{{{{\left( {1 - n} \right)}}^{2}}}}E(k) - K(k)} \right) \times 4n{{(1 - {{n}^{2}})}^{2}};$$
(B16)
other coefficients \(\Omega _{{klm}}^{{\left( 2 \right)}} = 0\).