INTRODUCTION

In a number of medical applications associated with local hyperthermia of human tissues, it is important to carry out painless deep temperature measurements with appropriate accuracy. Perhaps magnetic resonance thermometry will make it possible to solve this problem in the future [1]. However, this method requires expensive equipment, trained personnel, and specially prepared facilities. Therefore, the availability of alternative methods is extremely important if they provide adequate accuracy. For medical applications, the error in determining temperature should not exceed 0.5–1 K and the spatial resolution should be no worse than 5 mm.

It is proposed to use passive acoustic thermometry, the physical basis of which is the recording of the thermal acoustic radiation of an object [2–4]. Noise signal measurements lead to a significant integration time: to achieve the required accuracy in the megahertz range, it is necessary to average the signal over 30–50 s. To reduce this time without loss of accuracy, it is proposed to use the heat conduction equation with blood flow (the Pennes equation [5]) when reconstructing temperature. In acoustic thermography, this approach has already been studied theoretically in various modifications [6, 7]. In the proposed algorithm, it is not the temperature itself that is reconstructed, but the parameters of the heat equation, while the desired parameters are not determined each time anew, but refined as measurements are taken. This approach has already been considered, including experimentally. When a model object, beef liver, was heated, the thermal diffusivity and the heating source were reconstructed [8]; when heated model objects, plasticine and Teflon, were cooled, the thermal diffusivity and initial temperature were reconstructed [9, 10]. The novelty is that this scheme considers blood flow in the human body.

The paper considers the one-dimensional case—on the one hand, the most physically transparent, and on the other hand, the most incorrect. If the temperature profile is reconstructed from the results of measuring thermal radiation at different frequencies, then it is impossible to distinguish between a narrow highly heated layer located at the same depth and a wide, but weakly heated one, with the existing measurement accuracy.

Let us mention study [11] in the field of microwave thermometry (mathematically, microwave and acoustic thermometry are described by similar equations), where the heat conduction equation (without blood flow) was used to reconstruct the temperature and the external heating of the object was considered, which corresponds to taking into account the boundary conditions. In this paper, it is proposed to consider local heating in depth in the human body, i.e., to introduce a source into the heat equation.

Thus, the paper proposes an algorithm for reconstructing the temperature profile during local tissue heating, taking into account the heat conduction equation with blood flow. The proposed algorithm has been tested experimentally.

MATERIALS AND METHODS

Calculation model. Let us consider a one-dimensional model of local hyperthermia of human soft tissues (see Fig. 1a). Changes in temperature \(T\) obey the heat conduction equation taking into account blood flow [5]:

$${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial t}}} \right. \kern-0em} {\partial t}} = {{a}^{2}}{{{{\partial }^{2}}T} \mathord{\left/ {\vphantom {{{{\partial }^{2}}T} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} - \eta \left( {T - {{T}_{0}}} \right) + S\left( x \right),$$
(1)

where \({{a}^{2}}\) is the thermal diffusivity coefficient, \({{\eta }}\) is blood flow, \({{T}_{0}}\) = 37°C is the temperature of incoming blood, \(S\left( x \right)\) is a heat source that does not change over time, \(x\) is the coordinate directed deep into the body, and \(t\) is time. We assume that the medium under study is homogeneous in terms of thermal diffusivity and blood flow \({{a}^{2}} = \) const, \({{\eta }} = \) const. The initial temperature distribution is \(T\left( {t = 0,x} \right) = {{T}_{0}}\); the boundary conditions are \(T\left( {t,x = 0} \right)\) \( = T\left( {t,x = \infty } \right) = {{T}_{0}}\).

Fig. 1.
figure 1

(a) Calculation model: sensor located at boundary of \(x = 0\) human body; parameters of heat equation: \({{\gamma }}\), absorption coefficient; \({{a}^{2}}\), thermal diffusivity coefficient; \({{\eta }}\), blood flow does not change spatially; heating source, which is determined by three parameters: Q, amplitude; \({{x}_{0}}\), depth of occurrence; d, width; reconstructed temperature distribution; \({{T}_{0}}\), temperature before heating. (b) Scheme of experiment: heating source in plastisol: resistance 400 Ω, to which a voltage of 18 V is applied; thermometers placed in plastisol.

Full size image

The acoustic brightness temperature measured by a sensor located at the boundary of the body at \(x = 0\) is calculated by the formula [12]

$${{T}_{A}}\left( t \right) = \gamma \int\limits_0^\infty T \left( {t,x} \right)\exp \left( { - \gamma x} \right)dx,$$
(2)

where \({{\gamma }}\) is the ultrasound absorption coefficient in terms of intensity. We assume that the medium under study is homogeneous in terms of absorption \({{\gamma }} = \) const.

Let us multiply both parts of Eq. (1) by the expression \({{\gamma }}\exp \left( { - {{\gamma }}x} \right)\) and integrate over X. In this case, the first term on the right-hand side of (1) is twice integrated by parts. As a result, taking into account expression (2), we obtain

$$\begin{gathered} \frac{{d{{T}_{A}}}}{{dt}} = \gamma {{a}^{2}}\left\{ { - \frac{{\partial T\left( {t,0} \right)}}{{\partial x}} - \gamma T\left( {t,0} \right) + \gamma {{T}_{A}}} \right\} \\ - \,\,~\eta \left( {{{T}_{A}} - {{T}_{0}}} \right) + \gamma \int\limits_0^\infty {S\left( x \right)} \exp \left( { - \gamma x} \right)dx. \\ \end{gathered} $$
(3)

Let us suppose that the heating source is located quite deeply and the heating time is short, so that the influence of the source on the temperature gradient on the surface of the body can be neglected: \({{\partial T\left( 0 \right)} \mathord{\left/ {\vphantom {{\partial T\left( 0 \right)} {\partial x \approx 0}}} \right. \kern-0em} {\partial x \approx 0}}\).

Ultimately, we obtain an ordinary differential equation for the acoustic brightness temperature:

$$\begin{gathered} \frac{{d{{T}_{A}}}}{{dt}} = - \left( {\eta - {{\gamma }^{2}}{{a}^{2}}} \right)\left( {{{T}_{A}} - {{T}_{0}}} \right) \\ + \,\,\gamma \int\limits_0^\infty {S\left( x \right)} \exp \left( { - \gamma x} \right)dx, \\ \end{gathered} $$
(4)

the solution of which is determined by the expression

$$\begin{gathered} {{T}_{A}}\left( t \right) = {{T}_{0}} + \frac{{\gamma \int\limits_0^\infty {S\left( x \right)} \exp \left( { - \gamma x} \right)dx}}{{\eta - {{\gamma }^{2}}{{a}^{2}}}} \\ \times \,\,\left[ {1 - \exp \left( { - \left( {\eta - {{\gamma }^{2}}{{a}^{2}}} \right)t} \right)} \right]. \\ \end{gathered} $$
(5)

In the case of weak blood flow \({{\eta }} = 0\) with a short heating time \(t \ll {1 \mathord{\left/ {\vphantom {1 {{{\gamma }^{2}}{{a}^{2}}}}} \right. \kern-0em} {{{\gamma }^{2}}{{a}^{2}}}}\), the acoustic brightness temperature increases linearly with time:

$${{T}_{A}}\left( t \right) = {{T}_{0}} + \gamma t\int\limits_0^\infty {S\left( x \right)} \exp \left( { - \gamma x} \right)dx.$$
(6)

Temperature reconstruction algorithm. Based on expressions (5) and (6), we can propose an algorithm for reconstructing the time-varying temperature profile: temporal Depending on the measured acoustic brightness temperature, the parameters of the heat conduction equation are determined, and then, using this equation, the temperature profile is calculated at each moment of time. Let us assume that the following are known: the thermal diffusivity, the source profile and its two parameters: the width d (taken from half the maximum value) and the position x0, as well as the ultrasound absorption coefficient. It is necessary to find the unknown parameters of the heat equation: blood flow \({{\eta }}\) and the amplitude of the source Q.

For example, let us consider a source in the form of a Gaussian:

$${{S}_{1}}\left( x \right) = 2Q\sqrt {\frac{{\ln 2}}{\pi }} \exp \left[ { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{2}}\ln 2}}{{{{{({d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2})}}^{2}}}}} \right],$$
(7)

then the integral presented on the right-hand side of expression (4), is equal to (for \({{x}_{0}} \gg d\))

$$\begin{gathered} \gamma \int\limits_0^\infty {{{S}_{1}}} \left( x \right)\exp \left( { - \gamma x} \right)dx \\ \approx \gamma Qd\exp \left( { - {{x}_{0}}\gamma } \right)\left( {1 + \frac{{{{d}^{2}}{{\gamma }^{2}}}}{{16\ln 2}}} \right). \\ \end{gathered} $$
(8)

To reconstruct the temperature, the following algorithm is proposed (see Fig. 2). The algorithm’s input parameters are: \({{a}^{2}}\), d, \({{x}_{0}}\), \({{\gamma }}\) and the experimental time dependence of the acoustic brightness temperature \({{T}_{A}}\left( t \right)\), which is approximated by a parabola \({{T}_{A}}\left( t \right) \approx {{T}_{0}} + {{k}_{1}}t + {{k}_{2}}{{t}^{2}}\)passing through the point \({{T}_{A}}\left( 0 \right) = {{T}_{0}}\), \({{k}_{1}}\) and \({{k}_{2}}\) are the calculated coefficients. If the resulting parabola is concave or close to a straight line, i.e., \({{k}_{2}} \geqslant 0\), indicating weak blood flow \({{\eta }} \approx 0\), then the acoustic brightness temperature is approximated by a straight line \({{T}_{A}}\left( t \right) \approx {{T}_{0}} + {{k}_{3}}t\). In this case, the output parameters \(Q = \frac{{{{k}_{3}}\exp \left( {\gamma {{x}_{0}} - {{{{d}^{2}}{{\gamma }^{2}}} \mathord{\left/ {\vphantom {{{{d}^{2}}{{\gamma }^{2}}} 8}} \right. \kern-0em} 8}\ln 2} \right)}}{{\gamma d}}\) and \({{\eta }}\) = 0. If the resulting parabola is convex, i.e., \({{k}_{2}} < 0\), then the acoustic brightness temperature is approximated by the expression \({{T}_{A}}\left( t \right) \approx {{T}_{0}} + \frac{{{{k}_{4}}}}{{\eta\text{*}}}\left[ {1 - \exp \left( { - \eta \text{*}t} \right)} \right]\). As well, \(Q = \frac{{{{k}_{4}}\exp \left( {\gamma {{x}_{0}} - {{{{d}^{2}}{{\gamma }^{2}}} \mathord{\left/ {\vphantom {{{{d}^{2}}{{\gamma }^{2}}} 8}} \right. \kern-0em} 8}\ln 2} \right)}}{{\gamma d}}\) and \(\eta = \eta {\text{*}} + \,\,{{\gamma }^{2}}{{a}^{2}}\) from parameters \(Q\) and \({{\eta }}\) according to Eq. (1).

Fig. 2.
figure 2

Algorithm for reconstructing blood flow \({{\eta }}\) and amplitude \(Q\) of source from experimental time dependence of acoustic brightness temperature \({{T}_{A}}\left( t \right)\). Thermal diffusivity \({{a}^{2}}\), width d, position x0 of source, and ultrasound absorption coefficient \({{\gamma }}\) are considered known.

Full size image

To assess the accuracy of the algorithm, we determine the errors in reconstructing the maximum temperature \({{T}_{{{\text{max}}}}} = T\left( {{{x}_{0}}} \right)\) and the size of the heated region h, taken at points where the temperature increase is equal to half the maximum \(T\left( {{{x}_{0}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right) - {{T}_{0}} = \) \(T\left( {{{x}_{0}} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right) - {{T}_{0}} = \) \({{\left( {{{T}_{{\max }}} - {{T}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\max }}} - {{T}_{0}}} \right)} 2}} \right. \kern-0em} 2}\). To determine these errors, a normally distributed error with a standard deviation is superimposed on the exact value of the time dependence of the acoustic brightness temperature \({{\delta }}{{T}_{A}}\). This error is determined from the threshold sensitivity of the acoustic thermograph. From to the acoustic brightness temperature specified with the error, the above algorithm determines parameters \(Q\) and \({{\eta }}\); from Eq. (1), the temperature is calculated and the maximum temperature and size of the heated region are determined. This procedure was repeated 1000 times. This made it possible to statistically determine the reconstruction errors (standard deviations) for the maximum temperature and size of the heated region.

Experimental testing of the algorithm. The temperature reconstruction algorithm was tested for heating of a model object: plastisol (transparent plastisol, hardness 15–17, Alpina Plast, Klin, Russia), the acoustic and thermophysical properties of which are close to those of soft tissues of the human body [13, 14]. A heater was placed in the plastisol, at a distance of 50 ± 3 mm from the surface, with a resistance of 400 Ω, to which a voltage of 18 V was applied. The temperature of the plastisol was controlled by two DS18S20P digital thermometers (Maxim Integrated, San Jose, USA) with an accuracy of 0.3 K. The sensors were located at distances of 20 ± 3 and 41 ± 3 mm from the boundaries of the plastisol (see Fig. 1b).

To measure the thermal acoustic radiation, a multichannel acoustic thermograph was used [15–17], developed by A.D. Mansfeld and currently being revised by R.V. Belyaev (bandwidth 1.6–2.5 MHz, threshold sensitivity with an integration time of 10 s, 0.2 K). The received acoustic signals were converted into electrical signals, which were amplified, passed through a quadratic detector, and averaged over 30 ms. From the outputs of the multichannel acoustic thermograph, the signals were fed to an E14-140 14-bit multichannel ADC (ZAO L-Card, Moscow, Russia) at a sampling rate of 1 kHz per channel. The developed program subsequently averaged the data.

Before measurements, the acoustic sensor was in a holder, which was an acoustic blackbody at room temperature. The thermal acoustic radiation of the plastisol was measured for 10–15 s. For the acoustic contact, Mediagel ultrasound gel was applied to the surface of the object. After measurements, the sensor was returned to the holder until the next measurement. The interval between measurements was about 1 min.

RESULTS

Choice of parameters. Normally, blood flow in different tissues of the body varies widely [14] from 28–38 mL/(kg min) or (4.7–6.3) × 10–4 1/s in adipose tissue–skeletal muscle up to 1050–5000 mL/(kg min) or (1.75–8.33) × 10-2 1/s in the liver–thyroid gland. The thermal diffusivity varies insignificantly in tissues [14]; e.g., at 37°C, the thermal diffusivity in the liver is 0.141, and in adipose tissue, 0.131 mm2/s. Variations in this parameter with changes in temperature are also small: e.g., in liver, 0.28%/deg. To estimate the size of the source, we use the following reasoning. Let us assume that heating is by an optical fiber introduced into the body, through which IR radiation is transmitted. This radiation is absorbed in the depths of the body, generating heating. According to [14], the characteristic penetration depth (the distance at which the light intensity decreases by e times) in the liver at wavelengths of 800 and 1000 nm is 1 and 0.5 mm, respectively, and in the kidneys at the same wavelengths, 2.7 and 1.6 mm, respectively. Note that the source is not a Gaussian when radiation is absorbed, but calculations show that the shape of the source has little effect on the shape of the temperature distribution. The frequency dependence of the ultrasound attenuation coefficient in soft tissues is usually given by the empirical formula \({{\gamma }} = a{{f}^{b}}\) [14]. For example, for the liver and thigh muscles, the coefficient b = 1, the coefficient a = 0.162 and 0.128 1/(mm MHz), respectively. In this case, at a frequency of 2 MHz, the attenuation coefficient is 0.0324 and 0.0256 1/mm, respectively.

After analyzing the literature for the calculated model, the following parameters of the heat equation were selected: \({{x}_{0}}\) = 25 mm, d = 4 mm, a2 = 0.14 mm2/s, \({{\gamma }}\) = 0.03 1/mm.

The normally distributed random error corresponding to the threshold sensitivity of the acoustic thermometer 0.2 K for 10 s is superimposed on the calculated acoustic brightness temperature [18].

Figure 3 shows the effect of blood flow on temperature, which presents the temperature profiles in different tissues with different blood flows with a source in the form of a Gaussian. Let the doctor’s task be to heat some area in 5 min to the optimum temperature, e.g., to 43°C. Note that in cases without blood flow and for skeletal muscles on the presented scale, the temperature profiles almost completely coincide. The width of the heated region with an increase in blood flow by more than two orders of magnitude (skeletal muscles–thyroid gland) decreases insignificantly, by 6 mm. With significant blood flow, the width of the temperature distribution tends to the width of the source.

Fig. 3.
figure 3

Profiles of source (one) and temperatures after 5 min heating in different tissues. Calculation parameters: \({{a}^{2}} = \) 0.141 mm2/s, \({{x}_{0}} = \) 25 mm d = 4 mm; without blood flow 2), Q = 0.035 K/s; skeletal muscles (3), Q = 0.038 K/s, \({{\eta }} = \) 6.3 × 10–4 1/s; brain (4), Q = 0.087 K/s, \({{\eta }} = \) 9.3 × 10–3 1/s; liver (5), Q = 0.139 K/s, \({{\eta }} = \) 1.75 × 10–2 1/s; thyroid (6) – Q = 0.545 K/s, \({{\eta }} = \) 8.33 × 10–2 1/s. On presented scale, temperature profiles without blood flow and for skeletal muscles almost completely coincide (2 = 3).

Full size image

Calculating the acoustic brightness temperature. Figure 4 shows the time dependences of the acoustic brightness temperature calculated by formula (2) without and with blood flow as in the liver. For example, six acoustic brightness temperature samplings are shown with an error \({{\delta }}{{T}_{A}}~\)= 0.2 K. Figure 4a shows that the acoustic brightness temperature without blood flow increases linearly, while the increase in the maximum temperature slows, but the size of the heated region increases. The acoustic brightness temperature is determined by the integral of the deep temperature distribution (i.e., proportional to the product of the maximum temperature and size of the heated region) and therefore increases linearly with time over a given time interval.

Fig. 4.
figure 4

Time dependences of acoustic brightness (1) and maximum (2) temperature, as well as width (3, dotted line) of heated region (a) without and (b) with blood flow as in liver. Calculation parameters: \({{a}^{2}} = \) 0.141 mm2/C, \({{x}_{0}} = \) 25 mm, d = 4 mm, \(\gamma = \) 0.03 1/mm; without blood flow 2), Q = 0.035 K/s; liver (5), Q = 0.139 K/s, 1.75 × 10–2 1/s. Six samplings are superimposed on exact acoustic brightness temperatures with error of \({{\delta }}{{T}_{A}}\) = 0.2 K. Reconstruction errors (standard deviations) calculated from 1000 samplings are shown. Without blood flow, width of heated region is determined without error.

Full size image

Reconstructing the temperature distribution. The first time, reconstruction was done 50 s after the onset of heating and was repeated every 50 s for 5 min. Whereas for the first time data were used only for the first 50 s of heating, later this time increased: the second time, the temperature was reconstructed in 100 s; the third time, in 150 s; etc. The final reconstruction used all the data acquired in 5 min.

The problem of reconstructing the maximum temperature without blood flow is linear, and the error of its solution \({{\delta }}{{T}_{{{\text{max}}}}}\) is proportional to the expression \(\delta {{T}_{{\max }}}\sim {{\delta {{T}_{A}}} \mathord{\left/ {\vphantom {{\delta {{T}_{A}}} {\sqrt {\sum {{t}_{i}}^{2}} }}} \right. \kern-0em} {\sqrt {\sum {{t}_{i}}^{2}} }}\), where \({{t}_{i}}\) are the times of acoustic brightness temperature measurements. Thus, for its calculation, it was not necessary to calculate samplings of the random process. However, this was done in order to validate the proposed approach before using it in the case of high flow. The temperature reconstruction error is shown in Fig. 4a. When integrating data in 50 s, the error was 0.8 K; for 150 s, it decreased to 0.4 K; when integrating over the entire measurement time, it was 0.25 K.

Without blood flow, the width of the temperature distribution depends on time, but for the given time it does not depend on the source amplitude . Therefore, the reconstructed size of the temperature distribution coincides with the initial one.

Reconstruction with blood flow as in the liver. The problem of reconstructing the maximum temperature and width of the heated region in the presence of blood flow is nonlinear and was solved numerically. The maximum temperature reconstruction error is shown in Fig. 4b. When integrating data in 50 s, the error was 1.2 K; for 150 s it decreased to 0.45 K; when integrating over the entire measurement time, it was 0.27 K.

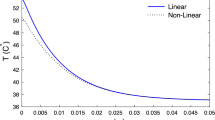
Experiment with Plastisol. The plastisol was heated for 33 min. The measured acoustic brightness temperatures and electronic thermometer data (before, during, and after heating) are shown in Fig. 5. The initial temperature of the plastisol was 20.1°C. Note that the acoustic brightness temperature and temperature measured at a distance of 20 mm from the surface of the plastisol (i.e., 30 mm from the center of heating) did not immediately begin to decrease after the end of heating. The measurement results were used to determine the coefficient k3 = 0.0016 K/s and calculate the source amplitude Q = 0.05 K/s (at \({{a}^{2}} = \) 0.15 mm2/s [13], d = 2 mm \({{x}_{0}} = \) 50 mm \({{\gamma }} = \) 0.03 1/mm [13]). Equation (1) was used to calculate the time dependences of the temperature at the locations of the electronic thermometers: the temperature ranges within ± 3 mm are shown in Fig. 5. It can be seen from the graphs that the proposed algorithm works.

Fig. 5.
figure 5

Time dependences of measured acoustic brightness temperature (1, ⚪—up to, ⚫—during, ◻—after heating) and readings of electronic thermometers located at distances 20 ± 3 (2) and 41 ± 3 (3) mm from plastisol boundaries. Calculated dependences: acoustic brightness temperature approximated by straight line (1), temperature ranges (shown in gray) at thermometer locations (2' and 3'). Acoustic brightness temperature measurement error is shown for rightmost marker. 0, onset; 33 min, end of heating.

Full size image

DISCUSSION

Of the three source parameters—depth, width, and amplitude—only the last was reconstructed. This is because the remaining parameters can be determined a priori, before the onset of heating. If heating is done via a light guide introduced into the body, through which infrared radiation is transmitted, then the position of the tip of the light guide is controlled using standard medical ultrasound. The width of the source can be premeasured in a model experiment. Theoretically, in an experiment using a model, it is also possible to measure the source amplitude (in this case, in the proposed algorithm, it remains only to determine the blood flow), but in reality, this characteristic depends on the state of the fiber tip that comes in contact with tissue. When heated, burnt tissue can form, which prevents the passage of radiation from the fiber to the surrounding tissue, which cannot be controlled a priori [19].

The choice of maximum temperature is associated with the use of hyperthermia in oncology. In [20], a reference temperature of 43°C was proposed to assess the thermal dose under conditions clinically significant for biological impact. In this case, the heat dose, expressed in min, is equal to the heating time.

The maximum temperature and size of the heated region were taken as the reconstruction parameters. This is because these parameters are convenient for use when controlling hyperthermia: doctors are primarily interested in information about the size and temperature of the heated region, not about the temperature distribution.

Note the fundamental nature of the result: as is known, it is impossible to reconstruct the temperature distribution from data on the acoustic brightness temperature at a given point in time: it is impossible to reconstruct the function from a point. This can be done if the frequency dependence of the acoustic brightness temperature is measured, which is related to the frequency dependence of the absorption coefficient [21]. In this study, the problem is solved in a different way: the time dependence of the acoustic brightness temperature is considered, and the parameters of the heat equation are reconstructed from it. After integrating the equation, the time-varying temperature distribution is reconstructed. The requirement that the temperature satisfy the heat equation leads to increased reconstruction accuracy. Each time (after 50, 100, …, 300 s) the required parameters are not determined anew, only refined (see [5, 7]). The integration time practically increases, but the temporal resolution does not suffer: new results can be obtained after any period of time. This advantage is achieved by requiring that the parameters of the heat equation remain constant. Note that this requirement, generally speaking, is inapplicable to blood flow: when tissue is heated, it increases. In this case, it is necessary to find a constant parameter of the changing blood flow, e.g., to assume that the blood flow grows linearly [22]. This is the topic of a separate study.

Note that the shape of the source is not critical for temperature reconstruction. If we compare rectangular and Gaussian sources located at the same depth, with the same width and area along the curve of the source, then with 5 min heating at the same maximum temperature of 43°C, the sizes of the heated regions differ by less than 1 mm and the acoustic brightness temperatures differ by less than 0.03°C.

Let us consider the applicability limits of the model associated with the boundary conditions. A significant limitation is the zero temperature gradient at the boundaries of the region. This means that all heat remains in the area, which can only be considered true at the onset of heating. Thus, for a weak blood flow, the model can be considered adequate as long as the acoustic brightness temperature increases linearly with time.

Let us show the limitations of the model associated with the acoustic inhomogeneity of the medium. Ultrasound absorption is different in different bodily tissues. If changes in the absorption coefficient correlate with changes in temperature, then the acoustic brightness temperature changes. For example, if absorption in the heated region is greater than the average, then this will increase the acoustic brightness temperature. However, according to [14], the temperature dependence of the ultrasound attenuation coefficient in soft tissues at a temperature of ~37°C at a frequency of ~2 MHz is almost completely absent: the temperature coefficient is 0 ± 0.4 (m K)–1. If the absorption does not depend on temperature, then the spatial inhomogeneity of absorption does not lead to significant changes in the acoustic brightness temperature due to the integral nature of this characteristic.

In various soft tissues of the body, the sound speed is different. According to [14], the sound speed in the liver and muscle tissue varies from 1568 to 1593 m/s or ±1.6%. These speed variations lead to a change in the hardware function (directivity pattern) of the receiving device, which must be taken into account in the 3D model.

Note the illustrative nature of experimental testing of the algorithm. The experimental conditions did not fully correspond to the numerical calculation parameters: a heating time six times longer; the local source an unheated layer parallel to the surface; the presence of reflection from the resistance placed in the plastisol. However, the problem of experimental verification of the accuracy of the proposed algorithm was not posed. It is important to use the proposed approach to solving the 3D inverse problem, taking into account the instrumental function of the acoustic sensor [23]. This is a topic for future research.

CONCLUSIONS

The proposed algorithm makes it possible to reconstruct the temperature and size of the heated region with an accuracy acceptable for medical applications. This accuracy is reached 2 min after the onset of heating, after which the temperature distribution can be monitored almost continuously. This result is achieved by using the heat equation. The algorithm has been experimentally verified.