1 INTRODUCTION

The study of oceanic ship noise at different distances from a vessel, as well as the use of this noise to solve the inverse problem, has recently attracted attention for several reasons:

— active navigation and constant presence of intense noise underwater;

— most of the noise energy is in the low-frequency region: the typical ship noise spectrum is irregular with a set of discrete components and is mainly in the frequency range from 20 to 200–300 Hz. This, first, ensures fairly long sound propagation and its penetration into the bottom, which can be used in solving inverse problems, and second, it makes it possible to minimize the use of massive low-frequency sound emitters.

Among studies on the possibility of using ship noise to determine the characteristics of the underwater environment and bottom, the following studies are noteworthy. In [1], identification of anthropogenic and natural noise components in the ocean is studied; the authors of [2] consider the possibility of using a noisy line (navigation route) as a nonlocal noise source for passive diagnostics of the temperature front in the Ushant region. In [3], a towed horizontal array was used to record noise, with subsequent solution of the inverse problem. The noise source was the towing vessel itself. In [4], the noise of a moving ship was recorded with a vertical array, followed by waveguide mode selection, determination of their attenuation coefficients, and estimation of the sound speed in the bottom based on these coefficients. In [5], ship noise was recorded by an autonomous unmanned underwater vehicle in very shallow water, with further estimation of the longitudinal wave velocity in the bottom. The inverse problem of determining the bottom parameters was also solved based on data from the Shallow Water 2006 experiment [6], using a record of ship noise from an L-shaped array.

In contrast to the above studies, here we analyze the noise of a moving ship simultaneously on two synchronized closely spaced vertical chains of hydrophones (arrays), which cover most of the waveguide in depth; simultaneous coherent processing of signals from these two chains is applied. The studies were carried out in a shallow waveguide with a gas-saturated upper layer of bottom sediments (Lake Kinneret, Israel).

2 EXPERIMENTAL

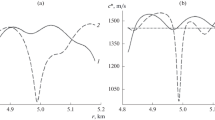
Figures 1 and 2 show the scheme of the field experiment, which was carried out in the central part of Lake Kinneret, where the depth is approximately 40.4 m; the sound velocity profile \(c\left( z \right)\) is characterized by a noticeable jump at a depth of 10–15 m (Fig. 1b). The bottom of the water area is covered with gas-saturated sediments, the gas concentration in which is maximum in the center of the lake [7]. The receiving system consisted of two vertical synchronized chains of hydrophones (Figs. 1b, 2) fixed on the bottom near a moored platform, spaced approximately \({{\Delta }}r\) = 40 m from each other, one of which we conditionally call the western (W), and the other, the eastern (E). Each chain consisted of \(N = ~\)10 hydrophones placed at an interval \({{\Delta }}z = ~\) 3 m, covering the depth range from 10 to 37 m.

Fig. 1.
figure 1

(a) Bathymetric map of lake showing location of arrays and ship’s trajectory; (b) vertical sound velocity profile in water layer and depth of hydrophones on arrays.

Full size image
Fig. 2.
figure 2

General scheme of experiment.

Full size image

The experimental scheme in Fig. 2 shows the movement of the noise signal source, the—R/V Hermona, along a straight line through both arrays, with the eastern chain always closest to the vessel. The study considers a time interval of ~5 min, during which the vessel moved at a speed of 4 m/s away from the arrays to a maximum distance of 1000 m. Figure 3a shows an example of the noise signal spectrum received by different hydrophones of the western array is shown in Fig. 3a; Fig. 3b, the spectra averaged over hydrophones on two arrays. Clearly, the ship’s noise spectrum has significant maxima in the region of 20–30 and 80–100 Hz. At the same time, at higher frequencies, the spectrum is quite uniform.

Fig. 3.
figure 3

(a) Example of spectrum of signal received by hydrophones of western array; (b) spectra of received signal by eastern and western arrays, averaged over array elements. Spectra are normalized to maximum value in range of 20–500 Hz.

Full size image

3 DATA PROCESSING AND RESULTS

We consider the field from a noise source recorded by the two arrays (E, W), namely, the time dependence of the sound pressure on various hydrophones \({{P}^{{\text{E}}}}\left( {t,{{z}_{j}}} \right)\) and \({{P}^{{\text{W}}}}\left( {t,{{z}_{j}}} \right)\), where \({{z}_{j}}\) is the hydrophone depth and \(t\) is the “fast” time in the time interval of the ship’s movement. After calculating the spectrograms as functions of frequency \({{\omega }} = 2{{\pi }}f\) and “slow” time T in the range from 0 to 5 min, we obtain the functions \({{P}^{{\text{E}}}}\left( {{{\omega }},T,{{z}_{j}}} \right)\) and \({{P}^{{\text{W}}}}\left( {{{\omega }},T,{{z}_{j}}} \right)\), respectively. Examples of the ship noise spectrograms are shown in Fig. 4 for the central hydrophones of both arrays. When taking a spectrogram, the window width was chosen as 1 s, and adjacent windows did not overlap.

Fig. 4.
figure 4

Spectrograms of ship noise recorded by central hydrophones (a) of western and (b) eastern arrays.

Full size image

Assuming a regular waveguide in the area of the ship’s movement with a constant depth \(~H\) and known sound velocity profile in the water layer\(~c\left( z \right)\), we determine the waveguide modes \({{{{\psi }}}_{m}}\left( {z,{{\omega }}} \right)\) as the solution to the Sturm–Liouville eigenvalue problem:

$$\frac{{{{d}^{2}}{{{{\psi }}}_{m}}\left( {z,{{\omega }}} \right)}}{{d{{z}^{2}}}} + \left( {{{{{{{\omega }}}^{2}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}^{2}}} {{{c}^{2}}\left( z \right)}}} \right. \kern-0em} {{{c}^{2}}\left( z \right)}} - \xi _{m}^{2}} \right){{{{\psi }}}_{m}}\left( {z,{{\omega }}} \right) = 0$$
(1)

with the corresponding boundary conditions on the surface (\({{{{\psi }}}_{m}}\left( {0,{{\omega }}} \right) = 0\)) and bottom (continuity of ψ and relations \(\frac{1}{{{{\rho \psi }}}}\frac{{d{{\psi }}}}{{dz}}\) at \(z = H\), where \({{\rho }}\) is the density of the medium); \({{{{\xi }}}_{m}}\)= \({{q}_{m}} + {{i{{\gamma }_{m}}} \mathord{\left/ {\vphantom {{i{{\gamma }_{m}}} 2}} \right. \kern-0em} 2}\) are complex eigenvalues.

A peculiarity of this problem is that we do not know the properties of the bottom, and we cannot use the boundary conditions for \(z = H\). However, we have sound field records by the two arrays at our disposal. Next, we present a scheme for finding the eigenfunctions and eigenvalues using the ship’s noise and two synchronized arrays.

Let us construct a solution to the equation

$$\frac{{{{d}^{2}}{{\psi }}\left( {z,{{\omega }},q} \right)}}{{d{{z}^{2}}}} + \left( {{{{{{{\omega }}}^{2}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}\left( z \right) - {{q}^{2}}} \right){{\psi }}\left( {z,{{\omega }},q} \right) = 0$$
(2)

with the boundary condition \({{\psi }}\left( {{{\omega }},q,0} \right) = 0\), with a continuous change in parameter \(q\). Next, we find the expansion coefficients of the spectrograms, where instead of a continuous quantity \(z\), discrete depth values are used (depths of ten hydrophones \({{z}_{j}}\)); these coefficients are functions of the parameter \(q\), frequencies \({{\omega }}\), and slow time \(T\):

$${{A}^{E}}\left( {{{\omega }},T,q} \right) = \mathop \sum \limits_{j = 1}^N {{P}^{{\text{E}}}}\left( {{{\omega }},T,{{z}_{j}}} \right){{\psi }}\left( {{{z}_{j}},{{\omega }},q} \right){{\Delta }}z,$$
(3)
$${{A}^{W}}\left( {{{\omega }},T,q} \right) = \mathop \sum \limits_{j = 1}^N {{P}^{{\text{W}}}}\left( {{{\omega }},T,{{z}_{j}}} \right){{\psi }}\left( {{{z}_{j}},{{\omega }},q} \right){{\Delta }}z.$$
(4)

Next, we write the amplitude ratio \({{A}^{{\text{E}}}}\) and \({{A}^{{\text{W}}}}\) taking into account the compensation of the phase shift at a distance \({{\Delta }}r\) between the arrays; we take the real part and average over the slow time (or over the distance from the arrays to the ship), which yields

$$R\left( {{{\omega }},q} \right) = {{\left\langle {{\text{Re}}\left( {\frac{{{{A}^{{\text{E}}}}\left( {{{\omega }},T,q} \right)}}{{{{A}^{{\text{W}}}}\left( {{{\omega }},T,q} \right)}}\exp \left( {iq{{\Delta }}r} \right)} \right)} \right\rangle }_{T}}.$$
(5)

When processing the experimental data, we took the median average. Let us now construct the function \(R\) in (\({{\omega }}\), \({{v}_{{{\text{ph}}}}}\)) coordinates, where \({{v}_{{{\text{ph}}}}} = {{{\omega }} \mathord{\left/ {\vphantom {{{\omega }} q}} \right. \kern-0em} q}\) is the phase velocity. The result is shown in Fig. 5 in normal (Fig. 5a) and enlarged (Fig. 5b) scales. The regions of the maxima observed on this plane in the form of hyperbolas correspond to the dispersion dependences—the dependences of the phase velocity of the waveguide mode \({{v}_{{{\text{ph}},m}}}\) on frequency \({{\omega }}\)—for 12 mode. In while, these figures also show the dispersion curves of the modes for a waveguide with a perfectly soft bottom and constant sound speed of in the water layer \({{c}_{0}} = {{\min }_{{\text{z}}}}\left( {c\left( z \right)} \right)\): \(v_{{{\text{ph}},m}}^{0}\left( {{\omega }} \right) = \frac{{{\omega }}}{{\sqrt {{{{\left( {\frac{{{\omega }}}{{{{c}_{0}}}}} \right)}}^{2}} - {{{\left( {\frac{{{{\pi }}m}}{H}} \right)}}^{2}}} }}\), where \(m\) is the mode number. The experimental dependences \({{v}_{{{\text{ph}},m}}}\left( {{\omega }} \right)\) were close to the similar dependences for a waveguide with a perfectly soft bottom \(v_{{{\text{ph}},m}}^{0}\left( {{\omega }} \right)\) except for the frequency range near the cutoff frequency (see Fig. 5a).

Fig. 5.
figure 5

(a) Distribution of \(R\) in \(\left( {{{\omega }},{{V}_{{{\text{ph}}}}}} \right)\) coordinates: frequency of sound and phase velocity of mode; (b) enlarged image of same distribution. White hyperbolas show dispersion curves for modes in waveguide with perfectly soft bottom.

Full size image

It is of interest to present Fig. 5a in \(\left( {{{\omega }},m{\text{*}}} \right)\) coordinates, where

$$m{\text{*}}\left( {{\omega }} \right) = \frac{{H{{{{\sigma }}}_{m}}\left( {{\omega }} \right)}}{{{\pi }}} = \frac{{{{\omega }}H}}{{{\pi }}}\mathop {\max }\limits_{\text{z}} \left( {\sqrt {\frac{1}{{{{c}^{2}}\left( z \right)}} - \frac{1}{{v_{{{\text{ph}},m}}^{2}\left( {{\omega }} \right)}}} } \right)$$

is the mode number assuming perfect softness of the bottom. (It is easy to show that these dependences also describe the dispersion curves of leaky modes in a homogeneous water layer above a fluid half-space, where the sound speed is much less than the sound speed of in water.) The result is shown in Fig. 6. The unshaded region corresponds to frequencies below the cutoff frequency for an ideal waveguide, i.e., when the radical expression is negative. The white straight lines in the same figure mark the integer values of the mode numbers. As can be seen, the observed maxima \(R\left( {{{\omega }},m{\text{*}}} \right)\) in most cases fit the theoretical lines quite well.

Fig. 6.
figure 6

Distribution of \(R\) in \(\left( {{{\omega }},m{\text{*}}} \right)\) coordinates: frequency of sound and mode number. White horizontal lines are drawn for integer values of mode number: \(m* = 1,~2,~3, \ldots \). Gray triangular region corresponds to frequencies below cutoff frequency for waveguide with perfectly soft bottom.

Full size image

In addition, based on the obtained \(v_{{{\text{ph}}}}^{m}\left( {{\omega }} \right)\), we can find the eigenvalues, or rather their real parts, as a function of frequency \({{q}_{m}}\left( {{\omega }} \right)\). Knowing the eigenvalues, the corresponding mode amplitudes on the arrays can be written as \(A_{m}^{{\text{E}}}\left( {{{\omega }},T} \right) \equiv {{A}^{{\text{E}}}}\left( {{{\omega }},T,{{q}_{m}}\left( {{\omega }} \right)} \right)\) and \(A_{m}^{{\text{W}}}\left( {{{\omega }},T} \right) \equiv {{A}^{{\text{W}}}}\left( {{{\omega }},T,{{q}_{m}}\left( {{\omega }} \right)} \right)\), and their ratio, in the form \({{R}_{m}}\left( {{{\omega }},T} \right)\) \( = {{A_{m}^{{\text{E}}}\left( {{{\omega }},T} \right)} \mathord{\left/ {\vphantom {{A_{m}^{{\text{E}}}\left( {{{\omega }},T} \right)} {A_{m}^{{\text{W}}}\left( {{{\omega }},T} \right)}}} \right. \kern-0em} {A_{m}^{{\text{W}}}\left( {{{\omega }},T} \right)}}\). Comparison of the mode amplitudes on the two arrays makes it possible to estimate the mode attenuation coefficients at different frequencies:

$$\begin{gathered} {{R}_{m}}\left( {{\omega }} \right) = {{\left\langle {{\text{Re}}\left( {\frac{{A_{m}^{{\text{E}}}\left( T \right)}}{{A_{m}^{{\text{W}}}\left( T \right)}}\exp \left( {i{{q}_{m}}\left( {{\omega }} \right){{\Delta }}r} \right)} \right)} \right\rangle }_{T}} \\ \approx \exp \left( {\frac{{{{\gamma }_{m}}\left( {{\omega }} \right)}}{2}{{\Delta }}r} \right). \\ \end{gathered} $$
(6)

Hence, the mode loss coefficient

$${{\gamma }_{m}}\left( {{\omega }} \right) = \frac{{2\ln {{R}_{m}}\left( {{\omega }} \right)}}{{{{\Delta }}r}}.$$
(7)

The application of such processing to the available experimental data is beyond the scope of this work and will be considered separately.

4 CONCLUSIONS

The paper proposes a new approach to separating normal modes and estimating their parameters by analyzing ship noise recorded by two synchronized closely spaced arrays. The advantage of this approach is that there is no need to know the exact coordinates and speed of the ship: it suffices to know only that it is moving in a straight line passing through both arrays. The approach makes it possible to estimate the dispersion characteristics of modes, which was demonstrated in the processing of field data, and also, in theory, to determine the frequency dependence of the modal damping coefficients.

Note that the experiment described above in Kinneret Lake is the first attempt to use this approach. The same method can apparently be applied in shallow water with an arbitrary trajectory of a noisy vessel, if this trajectory is known. Due to the nature of the signal processing, a high degree of accuracy in describing the ship’s trajectory is not required. This approach proved to be robust with respect to observed strong pseudoacoustic noise. However, the accuracy in extracting the dispersion curves will improve if the design of the arrays contributes to the suppression of inherent noise associated with flow around the arrays and their mechanical vibrations in the ship’s noise band. Additional studies are required to determine the optimal distance between vertical arrays for solving inverse problems.