Features of the Operation of a Three-Electrode Electrostatic Microgenerator in the Presence of Collisions between Electrodes

Abstract

The results of studying the influence of impact interactions on the operation of a three-electrode two-capacitor microelectromechanical transducer (MEMT) and a microgenerator based on it are presented. The operation of the microgenerator in the impact periodic mode is analyzed for two extreme cases, when the movable electrode initially comes into contact with the limiters located on the left (LWC) or right (RWC) walls of the casing. The relationship between the system parameters and the characteristics of the external driving force source, which makes it possible to evaluate the possibility of implementing a periodic impact operation, is obtained. The dependences of the average generated power of the impact microgenerator on the number of collisions and the load are calculated. It is shown that a microgenerator with a three-electrode MEMT, in the case when the movable electrode initially comes into contact with the limiters located on the LWC, develops more power than in the case when the movable electrode initially touches the limiters located on the RWC. The efficiency of the microgenerator in impact and nonimpact modes is compared. It is shown that when using the impact mode, a gain by factors of 2 to 5 in the developed power is possible with a significant decrease of 1 to 2 orders of magnitude of the optimal load resistance compared to using an equivalent impact-free mode. In general, the analysis carried out and the developed approach make it possible to significantly narrow the range of the search for the necessary system parameters at the preliminary design stage and reduce the design time.

1 INTRODUCTION

The intensive development of microsystem technology and recent achievements in the field of nanotechnology have created prerequisites for creating a number of miniature devices for various purposes with a wide range of practical applications (sensor microsystems, micromechanical systems of various kinds, miniature implantable biostimulators, etc.).

Currently, chemical (lithium-ion and lithium-polymer) sources are mainly used as the energy source for autonomous small equipment. However, chemical sources have limitations in terms of miniaturization, a significant dependence of the main parameters on temperature, require periodic recharging, and their specific energy does not exceed 1 kW/kg.

Over the past 20 years, the attention of academic and industrial communities to solve the problem of powering low-power electronic devices, such as intelligent wearable systems, biomechanical implants, and nodes of wireless sensor networks, has attracted the extraction of energy from environmental sources [1, 2]. Electrical energy can be converted from sunlight, wind, tide, current, mechanical vibrations, and other natural resources. The kinetic energy of human movement, vibrations and environmental noise is one of the most common sources of energy in the environment. Therefore, significant efforts are directed towards the development of highly efficient energy harvesters for converting mechanical kinetic energy into electrical energy.

Mechanical energy can be converted into electrical energy using electromagnetic [3, 4], piezoelectric [5, 6], electrostatic [7, 8], and triboelectric [9, 10] conversion mechanisms. From the point of view of compatibility with the integrated technology for the production of microelectromechanical systems (MEMSs), the most promising is the electrostatic principle of conversion. The operation of such electrostatic microelectromechanical transducers (MEMTs) is based on the change in the capacitance of a variable capacitor under the action of external mechanical oscillations (vibrations) [11–13]. In addition, the use of MEMS technology provides high reliability and noise immunity, low power consumption, and a significant gain in terms of weight, size and technical and economic parameters.

The development and improvement of MEMTs and microgenerators based on them are primarily aimed at increasing the average generated power, as well as reducing their weight and size parameters, in relation to which there are spatial restrictions on the design of devices that in affect their operation. Usually, in order to increase the power of the MEMT, there is a tendency to increase the depth of modulation of the capacitance of the variable capacitor η = C_max/C_min (here C_max and C_min are the maximum and minimum values of the capacitance of a variable capacitor) and the amount of charge ${{q}_{0}}$ taken from the primary power source. With miniaturization of the converter, both of these possibilities are significantly limited, since with a decrease in the interelectrode gap, C_min and the probability of an electrical breakdown increase.

Theoretically, the power of the MEMT can also be increased by reducing the duration of the energy conversion cycle and increasing the number of conversion cycles during the period of external mechanical oscillations, which can be achieved by using additional forces that arise in the system when the electrodes of the variable capacitor collide.

Such a new type of MEMT, impact transducers, currently seems to be promising [14–17]. In the literature, the influence of impacts on the nonlinearity affecting the characteristics of MEMT [16–19] was studied; the possibility of using impacts on the MEMT to increase the bandwidth of vibration frequencies was considered [15, 20, 21].

Of course, modern computers make it possible to obtain solutions of dynamic systems for any set of parameter values and initial conditions. However, in this case, undesirable (or desired) and even potentially emergency modes of operation that are possible in the system under study may fall out of consideration. In this situation, it is important to have a general idea of the features and capabilities of the basic analog of the studied model, i.e., about the qualitative picture of its behavior depending on the change in parameters.

In our previous work, we showed the possibility of increasing the output power of a microgenerator based on an impact MEMT with a single variable capacitor [22].

In this study, modeling and comparative analysis of the operation of electrostatic two-capacitor microgenerators containing a three-electrode MEMT of the impact and impact-free type are carried out.

2 MEMT MODEL

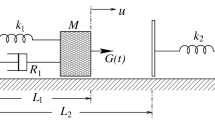
Before analyzing the operation of the microgenerator as a whole, let us consider the features of the functioning of its most important part: the MEMT. Like the classic electrostatic, the impact transducer is a variable capacitor. A simplified mechanical diagram of the three-electrode design of such a MEMT is shown in Fig. 1. The transducer contains a casing and a movable electrode. One of the electrodes of the variable capacitor is located on the right wall of the casing (RWC); the second one, on the left wall of the casing (LWC); and the third one, a movable electrode, can move freely between the left and right walls of the case. To prevent the movable electrode and electrodes located on the RWC and LWC from sticking, the latter are provided with limiters. In the analysis, it was assumed that the maximum value of the gap between the limiters and the movable electrode is d₀. The thickness of the movable electrode is zero. The height of the limiters was chosen proportional to the gap d₀ and equal to md₀, where m is the coefficient of proportionality.

Fig. 1.

Schematic representation of the design of a three-electrode energy transducer (a) and its mechanical model (b) used for simulation.

In the process of moving the casing according to the law y(t), determined by an external driving force (force excitation), a movable electrode with mass M₁, fixed on an elastic suspension with rigidity k, is involved in the oscillatory process and moves according to the law z(t) (kinematic excitation). In this case, the elastic forces of the suspensions act on the movable electrode from the side of the suspensions, seeking to return it to the equilibrium position, and the electric forces of attraction created by the applied electric field.

As a result, the gap between the limiters on the LWC and the movable electrode changes according to the law x(t). In this case, in a linear approximation for a mechanical force, the force balance equation can be represented as

$${{M}_{1}}\frac{{{{d}^{2}}h}}{{d{{t}^{2}}}} + B\frac{{dh}}{{dt}} + kh - {{F}_{e}} = - {{M}_{1}}\frac{{{{d}^{2}}y}}{{d{{t}^{2}}}},$$

(1)

where h = d₀ – x is the current value of the gap between the limiters on the RWC and the movable electrode, F_e is the electrical force, and B is the coefficient of mechanical resistance.

Equation (1) describes the movement of the movable electrode only in the time intervals between collisions with the limiters. To take into account the impact interaction at the moment of contact of the movable electrode with the limiters, we will use the method of deformable elements, within which a spring is mentally placed at the contact point, which has a very high rigidity and a negligible mass. In this case, if we take into account that immediately before the impact, the deformation of the spring δ(0) = 0 and the initial speed of the deformation of the spring is equal to the rate of convergence of the electrodes $\dot {\delta }(0) = {{v}_{1}}(0) - {{v}_{2}}(0)$, then with a linear dependence of the elastic force on the deformation

$$\delta (t) = \frac{{{{v}_{1}}(0) - {{v}_{2}}(0)}}{\omega }\sin (\omega t),$$

where $\omega = \sqrt {k{\text{/}}({{M}_{1}} + {{M}_{3}})}$, k is the coefficient of the spring’s stiffness, and ${{v}_{1}}$ and ${{v}_{2}}$ are, respectively, the speed of the movable electrode and the casing immediately before the contact of the electrodes. Under the assumptions made, the impact duration Δt = π/ω and the maximal impact force ${{F}_{{\max }}} = \sqrt {k({{M}_{1}} + {{M}_{3}})} ({{v}_{1}}(0) - {{v}_{2}}(0))$. If we assume that only the bumpers are deformed upon impact, then M₃ is the mass of the limiters on the wall of the case.

The estimates show that with four silicon limiters on the case wall with a height of 5 μm and a base area of 1 mm² each, the mass of the movable electrode is 1 g, and the impact duration will not exceed Δt = 1 µs. Thus, if the period of the change of the external force T (casing oscillation period) exceeds 1 ms, then the impact time can be neglected. Then, in the classical impact theory, the velocities of colliding bodies after impact will be determined by the equations [23, 24]

$$\begin{array}{*{20}{c}} {{{V}_{1}} = {{v}_{1}} + (1 + e)\frac{{{{M}_{2}}}}{{{{M}_{1}} + {{M}_{2}}}}({{v}_{2}} - {{v}_{1}}),} \\ {{{V}_{2}} = {{v}_{2}} + (1 + e)\frac{{{{M}_{1}}}}{{{{M}_{1}} + {{M}_{2}}}}({{v}_{1}} - {{v}_{2}}),} \end{array}$$

(2)

where M₂ is the weight of the casing, e is the velocity recovery coefficient upon impact, ${{v}_{1}}$ and ${{v}_{2}}$ are, respectively, the velocities of the movable electrode and the casing before the impact, and V₁ and V₂ are their velocities after the impact. When modeling, we take into account that the mass of the casing is much greater than the mass of the movable electrode and the impact barely changes the characteristics of the motion of the casing (i.e., V₂ = ${{v}_{2}}$). In addition, taking into account the fact that losses in single-crystal silicon can be very small (the quality factor Si of the elastic elements can reach several tens of thousands), we assume that e = 1 (absolutely elastic impact).

The calculation also shows that with a limiter height of 5 μm, the area of the movable electrode is 6 cm², the amplitude of oscillations of the casing is 20 μm, and the voltage V  between colliding electrodes is 20 V, the maximum impact force F_max will exceed the electrical force of attraction between the electrodes F_e by a factor of more than 1000. As a result, for the given system parameters and V ≤ 20 V, the influence of F_e on the motion parameters of the system can be neglected.

Let us analyze the features of the motion of the MEMT’s movable electrode in the absence of electrical forces, mechanical resistance, and suspension elastic forces.

We will assume that initially the transducer casing is in the extreme left position and then begins periodic movement to the right. In turn, the movable electrode at the initial moment can be located at an arbitrary distance from the fixed ones. The analysis shows that, depending on the initial position of the movable electrode, its further movements will differ significantly.

There are two most different initial conditions leading to different behavior of the movable electrode. In the first case, the movable electrode initially comes into contact with the limiters located on the LWC, and then pushed by the LWC it begins to move. In the second case, the movable electrode initially touches the limiters located on the RWC.

We consider the first case. We will assume that at the initial moment of time t₀ = 0, the movable electrode was in contact with the limiters on the LWC, and the casing itself was in the extreme left position. With the beginning of the motion of the casing to the right, the movable electrode, pushed by the LWC, will also begin to move. In the case of the harmonic law of casing motion y(t) = –A₀cos(ωt), their joint motion at the same speed will continue until the casing speed reaches the maximum value v₂(t₁ = T/4) = A₀ω (here A₀ and ω are the amplitude and circular frequency of the casing oscillations). After that (with t > t₁) the motion of the casing will slow down, and the movable electrode will continue to move at a speed of ${{v}_{1}}$(t₁) = ${{v}_{2}}$(t₁) = A₀ω. At the point in time t₂, the movable electrode will “catch up” with the limiters on the RWC and they will collide, after which the casing will continue to move at speed V₂(t) = ${{v}_{2}}$(t) = A₀ω sin(ωt); and the movable electrode, at a speed of V₁(t₂) = 2${{v}_{2}}$(t₂) – ${{v}_{1}}$(t₁). In the future, the movable electrode at moment t₃ may again come into contact with the limiters on the right or on the left side of the casing.

Using the system of equations (1) and (2), it is possible to calculate the dependences of the gaps h(t) and x(t) between the limiters on the walls of the casing and the movable electrode versus the time for various parameters of the MEMT.

The analysis shows that, in the general case, the displacement of the movable electrode relative to the casing is aperiodic; i.e., the system behaves stochastically [22, 25].

An example of the calculated displacement trajectory of the movable electrode is shown in Fig. 2.

Fig. 2.

The movable electrode displacement trajectory relative to the middle of the gap at d₀ = 5.8 µm.

With such a behavior of the movable electrode, even the average power developed by the microgenerator over the period of oscillation of the casing can change in time, which is inconvenient when using a microgenerator. From this point of view, it is of interest to search for solutions in which the movement of the movable electrode will be periodic.

In order for the functioning of the system to become periodic, it is necessary, when compiling a system of equations describing its behavior, to take into account that ${{v}_{1}}$(t) and V₁(t) should be equal, respectively, ${{v}_{1}}$(t + T) and V₁(t + T). Under the assumptions made in this case, in order to determine the moments of collision of the movable electrode with the limiters on the RWC for the given number of collisions per the period of oscillations of the casing (POC), it is possible to compose an appropriate system of transcendental equations. For example, for an MEMT with four collisions during the POC, the system of equations that determines the parameters of the MEMT takes the form

$$\begin{gathered} \frac{{{{d}_{0}}}}{{{{A}_{0}}}} = \cos (\omega {{t}_{2}}) - \cos (\omega {{t}_{1}}) + \sin (\omega {{t}_{1}})(\omega {{t}_{2}} - \omega {{t}_{1}}), \\ \cos (\omega {{t}_{2}}) - \cos (\omega {{t}_{3}}) \\ = \,\,[2\sin (\omega {{t}_{2}}) - \sin (\omega {{t}_{1}})](\omega {{t}_{3}} - \omega {{t}_{2}}), \\ 2\sin (\omega {{t}_{3}}) = 2\sin (\omega {{t}_{2}}) - \sin (\omega {{t}_{1}}), \\ \end{gathered} $$

(3)

where t₂ and t₃ are the moments in time of the first and second impacts, respectively. At the same time, the time of the third impact t₄ will be equal to T – t₃; and the time of the fourth impact t₅ = T – t₂.

From (3) it follows that under the assumptions made, periodic behavior will be possible only with a certain ratio between the amplitude of the casing oscillations A₀ and the maximum gap between the limiters on the RWC and the movable electrode d₀.

In the general case, we fail to obtain analytical expressions for estimating the required value of the d₀/A₀ ratio for the given number of collisions n per POC of the MEMT. However, the calculations show that with an error of less than 2% in the interval 1 < n < 20, the dependency ratio d₀/A₀ on the number of collisions of the movable electrode n with the limiters on the RWC over the period is closely approximated by the exponential function

$${{d}_{0}}(n){\text{/}}{{A}_{0}} = 0.596{{n}^{{ - \sqrt 3 }}}.$$

(4)

According to (4), to increase the number of collisions n during the POC at a constant amplitude of oscillations of the MEMT casing A₀, it is necessary to reduce the maximum gap between the limiters and the movable electrode d₀ or increase A₀ if we need to keep d₀.

In Fig. 3 the motion trajectories of the left and right walls of the casing, as well as the movable electrodes in the impact (with two impacts during the POC) and the corresponding nonimpact MEMT, are shown, calculated at A₀ = 2 × 10^–5 m, T = 0.02 s, and ${{d}_{0}} = (2\pi - 3\sqrt 3 ){{A}_{0}}{\text{/}}6$. For clarity, the beginning of the countdown is combined with the moment of the first impact of the movable electrode on the limiters on the RWC.

Fig. 3.

Trajectories of motion of the left (dashed line) and right (dotted line) casing walls, as well as motion electrodes in the impact (with two impacts (dots)) and nonimpact (solid line) MEMT.

In Fig. 4 the dependences of the change in the gaps between the movable electrode and the electrodes on the casing on time in the impact, with two impacts during the POC, and the corresponding nonimpact MEMT, are shown, calculated with the same parameters as in Fig. 3 and m = 0.25.

Fig. 4.

Dependences of the change in the gaps between the movable electrode and the electrodes on the RWC and LWC on time in the impact (with two impacts) (dotted line, gap to RWC; dashed line, gap to LWC) and the corresponding nonimpact (solid line, gap to RWC) MEMT.

In Fig. 5 the dependences are shown of the change in capacitance between the movable electrode and the electrode on the RWC on time in the impact, with two impacts during the POC, and the corresponding nonimpact MEMT, calculated with the same parameters as in Fig. 3, and the area of the movable electrode S = 6 × 10^–4 m².

Fig. 5.

Dependences of the change in capacitance between the movable electrode and the electrode on the RWC on time in the impact (with two impacts) (dotted line) and the corresponding nonimpact (solid line) MEMT.

An analysis of the similar dependences calculated for the MEMT with a large number of collisions shows that, at a constant limiter height, the maximum depth of capacitance modulation decreases with the increasing number of collisions. If, simultaneously with a decrease in the ratio d₀/A₀, the height of the limiters is proportionally reduced, then the maximum modulation depth of the capacitance of the MEMT remains unchanged. However, the amplitude of the bounces decreases (Fig. 6).

Fig. 6.

Dependence of the change in the gap between the movable electrode and the limiters on the RWC on time in the impact (with nine impacts) MEMT.

We also note that, in the considered case, by changing the relations d₀/A₀, we can get any value of the number of impacts n = 1, 2, 3, … for the period of oscillations of the casing.

We consider the second case. We will assume that at the initial moment of time t₀ = 0, the movable electrode was in contact with the limiters on the RWC, and the casing itself was (as in the first case) in the extreme left position. With the beginning of the motion of the casing to the right, the movable electrode remains in place until the limiter on the LWC at moment t₁ no longer touches it. In the case of the harmonic law of motion of the casing y(t) = –A₀cos(ωt) after the first collision, the movable electrode will begin to move at a speed of V₁(t₁) = 2${{v}_{2}}$(t₁) = 2A₀ωsin(ωt₁), and the casing will continue to move at a speed of V₂(t) = ${{v}_{2}}$(t) = A₀ω sin(ωt). In the future, the movable electrode at moment t₂ may again come into contact with the limiters on the right or on the left side of the casing.

In order for the behavior of the system to become periodic, it is necessary, as in the first case, when compiling a system of equations describing its behavior, to take into account that ${{v}_{1}}$(t) and V₁(t) should equal respectively ${{v}_{1}}$(t + T) and V₁(t + T). In this case, for example, for an MEMT with four collisions during the POC, the system of equations that determines the parameters of the MEMT takes the form,

$$\begin{gathered} \frac{{{{d}_{0}}}}{{{{A}_{0}}}} = 1 - \cos (\omega {{t}_{1}}), \\ \frac{{{{d}_{0}}}}{{{{A}_{0}}}} = \cos (\omega {{t}_{2}}) - \cos (\omega {{t}_{1}}) \\ + \,\,2{\kern 1pt} \sin (\omega {{t}_{1}})(\omega {{t}_{2}} - \omega {{t}_{1}}), \\ \sin (\omega {{t}_{2}}) = \sin (\omega {{t}_{1}}), \\ \end{gathered} $$

(5)

where t₁ and t₂ are the time of the first and second impact, respectively. At the same time, the time of the third impact t₃ will be equal to T – t₂; and the time of the fourth impact t₄ = T – t₁.

Analysis (5) shows that in this case periodic behavior will be possible for a certain number of impacts n = 4, 8, 12… for the period.

In the general case, we fail to obtain analytical expressions for estimating the required value of the ratio d₀/A₀ for the given number of collisions in this case as well. However, the calculations show that with an error of less than 2% in the interval 1 < n < 24 the dependency ratio d₀/A₀ on the number of collisions n of a movable electrode with limiters on the RWC during the POC is closely approximated by the exponential function

$${{d}_{0}}(n){\text{/}}{{A}_{0}} = 4.25{{n}^{{ - 1.35}}}.$$

(6)

In Fig. 7 the trajectories of the motion of the left and right walls of the casings, as well as the movable electrodes in the impact (with four impacts per POC) and the corresponding nonimpact MEMT, are calculated with the initial conditions corresponding to the second case, at A₀ = 2 × 10^–5 m, T = 0.02 s, d₀ = 1.292 × 10^–5 m and m = 0.

Fig. 7.

Trajectories of motion of the left (dashed line) and right (dotted line) walls of the casing, as well as movable electrodes in the impact (with four impacts) (points) and nonimpact (solid line) MEMT.

Figure 8 shows the dependences of the change in the gaps between the movable electrode and the electrodes on the casing, on time in the impact with four impacts per POC and the corresponding nonimpact MEMT, calculated with the same parameters as in Fig. 7 and m = 0.25.

Fig. 8.

Dependences of the change in the gaps between the movable electrode and the electrodes on the RWC and LWC on time in the impact (with four impacts) (dotted line, gap to RWC; dashed line, gap to LWC) and the corresponding nonimpact (solid line, gap to RWC) MEMT.

In Fig. 9 the dependences of the change in capacitance between the movable electrode and the electrode on the RWC on time are shown in the impact with four impacts per POC and the corresponding nonimpact MEMT, calculated for the same parameters as in Figs. 7 and 8, and the area of the movable electrode S = 6 × 10^–4 m².

Fig. 9.

Dependences of the change in capacitance between the movable electrode and the electrodes on the RWC and LWC on time in the impact (with four impacts) (dotted line, gap to RWC; dashed line, gap to LWC) and the corresponding nonimpact (dark solid line, gap to RWC; light solid line, gap to LWC) MEMT.

A comparison of (4) and (6) shows that for the same A₀ and n the required maximum gap between the limiters on the RWC and the movable electrode d₀ in the second case (when at the initial moment of time the movable electrode comes into contact with the limiters on the RWC) will be greater. Moreover, with an increase in n this difference increases. As a result, in transducers with the same number of impacts n per POC in the first case, the maximum and minimum capacities will be greater than in the second case.

Now, knowing the dependence of the change in the capacitance of the variable capacitor on time, it is possible to analyze the operation of the microgenerator as a whole.

3 ANALYSIS OF THE OPERATION OF A MICROGENERATOR WITH A THREE-ELECTRODE MEMT

The electrical circuit of the microgenerator with a three-electrode MEMT (Fig. 10) includes primary power sources V₁ and V₂, two switches Sw₁ and Sw₂, a three-electrode MEMT (Fig. 1), forming C₁ and C₂ with a grounded movable electrode, and the load resistance R.

Fig. 10.

Electrical circuit of a microgenerator with a three-electrode MEMT.

Before starting the operation, capacities C₁ and C₂ are charged by the short-term connection of the primary sources V₁ and V₂. Then the switches Sw₁ and Sw₂ are open. When the transducer casing vibrates, the movable electrode is displaced relative to the fixed ones, the capacitance C₁ and C₂ change in opposite directions, and the potentials of the fixed electrodes and the voltage across the load resistance R, which is used to do useful work, change.

The system of equations describing the operation of this microgenerator can be represented as

$$\begin{gathered} \frac{{\partial {{q}_{1}}}}{{\partial t}} = \frac{{{{q}_{2}}}}{{{{C}_{2}}(h(t))R}} - \frac{{{{q}_{1}}}}{{{{C}_{1}}(x(t))R}}, \\ \frac{{\partial {{q}_{2}}}}{{\partial t}} = \frac{{{{q}_{1}}}}{{{{C}_{1}}(x(t))R}} - \frac{{{{q}_{2}}}}{{{{C}_{2}}(h(t))R}}, \\ {{M}_{1}}\frac{{{{d}^{2}}h}}{{d{{t}^{2}}}} + B\frac{{dh}}{{dt}} + kh - {{F}_{e}} = - {{M}_{1}}\frac{{{{d}^{2}}y}}{{d{{t}^{2}}}}. \\ \end{gathered} $$

(7)

As the initial conditions, we will assume that the charges of the capacitors at the initial moment of time are, respectively, q_0.1 = V₁C₁(x(0)) and q_0.2 = V₂C₂(h(0)), where in the first case C₁(x(0)) = ε₀εS/(md₀) and C₂(h(0)) = ε₀εS/(md₀ + d₀), and in the second C₁(x(0)) = ε₀εS/(md₀ + d₀) and C₂(h(0)) = ε₀εS/(md₀); here ε₀ is the electrical constant, ε is the relative permittivity of the gas in the interelectrode gap, and S are the areas of fixed electrodes. Under the assumptions made, the dependences x(t) and h(t) for the first and second cases are in accordance with the methods described in Section 2.

In the general case, the solution of system (7) is found only numerically. However, as shown in [22, 26, 27], if the driving force changes according to the harmonic law, i.e., y(t) = –A₀cos(ωt), then in the steady state for a nonimpact microgenerator, the solution of system (7) can be represented in an analytical form. For an impact microgenerator, both in the first and in the second cases, the solution, even with a change in the driving force according to the harmonic law, is found numerically.

In Figs. 11 and 12 the dependences of the change in the normalized voltage on the capacitors C₁, C₂ and load resistance versus time for nonimpact and the corresponding impact (with two impacts per POC) MEMT, calculated for the first case with the same parameters as in Figs. 4 and 5: V₁ = V₂ = V₀ = 1 V and R = 3.3 × 10⁶ Ohm for nonimpact and R = 7.4 × 10⁵ Ohm for the corresponding impact microgenerators. The time interval in Figs. 11 and 12 corresponds to the steady state and the voltage across the load resistance is determined as U_R = U_C2 – U_C1.

Fig. 11.

Dependences of the change in the normalized voltage on capacitors C₁ (dashed line) and C₂ (dotted line), as well as load resistance (solid line), on time for a nonimpact MEMT.

Fig. 12.

Dependences of the change in the normalized voltage on capacitors C₁ (dashed line) and C₂ (dotted line), as well as load resistance (solid line), on time for an impact (with two impacts) MEMT.

It can be seen (Fig. 11) that the voltage across resistor R in a nonimpact microgenerator changes according to the harmonic law, which corresponds to the conclusions [22, 26, 27]. At the same time, the voltage on each capacitor does not change according to the harmonic law (Fig. 11), and with an increase in the displacement amplitude of the movable electrode, the voltage changes on the capacitors generally begin to occur at a frequency of 2ω, which is a consequence of the nonlinearity of system (7). In this case, the voltage across the load resistor will continue to change at frequency ω.

In the case of an impact microgenerator the voltages across the capacitors C₁ and C₂ and on the load resistance R do not change according to the harmonic law (Fig. 12) and are determined by changes in the gaps between the electrodes shown in Fig. 4.

A similar situation occurs in the second case. In this case, the dependences of the change in the normalized voltages on the capacitors C₁ and C₂ and load resistance on time for a nonimpact MEMT have a form that coincides with that shown in Fig. 11.

The dependences of the change in the normalized voltages on the capacitors C₁, C₂ and load resistance on time for an impact (with four impacts per POC) MEMT, calculated with the same parameters as in Fig. 8 (V₁ = V₂ = V₀ = 1 V and R = 3.6 × 10⁶ Ohm), are given in Fig. 13. The time interval in Fig. 13 also corresponds to the steady state, and the voltage across the load resistance U_R = U_C2 – U_C1.

Fig. 13.

Dependences of the change in the normalized voltage on capacitors C₁ (dashed line) and C₂ (dotted line), as well as load resistance (solid line), on time for an impact (four-impact) MEMT.

It can be seen that in this case, the voltages on the capacitors C₁ and C₂ and load resistance R for an impact microgenerator, do not change according to the harmonic law and are determined by changes in the gaps between the electrodes shown in Fig. 8.

To determine whether it is possible to achieve a gain in the generated power and energy delivered to the load when using impact MEMTs, we calculated the dependences of the energy transferred to the load and taken from the primary power source over the period of casing oscillations, as well as the energy transfer rate (power) on the load resistance for microgenerators with a different number of impacts n and the corresponding nonimpact microgenerators. Correspondence means that the impact and the corresponding nonimpact MEMT have the same ratios d₀/A₀ and limiter heights. When analyzing the operation of a nonimpact MEMT, n shows which impact MEMT corresponds to the parameters of this nonimpact MEMT.

The calculations showed that with an increase in the load resistance for both nonimpact and impact microgenerators, the energy transferred to the load during the POC and the developed power first increase and then decrease. In other words, there is a maximum and the corresponding optimal load resistance R_opt. At the same time, the energy taken from the primary power sources remains constant when the load resistance changes. At the same time, with an increase in the load resistance, the ratio of the energy transferred to the load during the POC to the energy taken from the primary power source also has a maximum. Note that the dependences shown in Figs. 11–13 are calculated with the corresponding R_opt.

In Fig. 14 dependences R_opt are given from the number of impacts n per POC for the impact and corresponding nonimpact microgenerators. These dependences on a double logarithmic scale have the form of straight lines and are accurately described by exponential functions of the form b₀n^b1. Taking into account [22, 26, 27], (4), and (6), it can be shown that for nonimpact generators R_opt(n) = 2/(ωC₀(n)), where C₀(n) = ε₀εS/[(0.5 + m)d₀(n)]. However, in the first case d₀(n) is determined by (4) (i.e., the maximum gap between the movable electrode and the limiters on the RWC), and in the second case, it is determined by (6) (i.e., the maximum gap between the movable electrode and the limiters on the LWC).

Fig. 14.

Dependences R_opt on the number of collisions n for impact (1, 3) and their corresponding nonimpact (2, 4) microgenerators. (1, 2) First case; (3, 4) second case.

Note that with an increase in n, the value of R_opt for impact microgenerators decreases faster than for nonimpact ones (Fig. 14).

In Fig. 15 the dependences of the maximum developed power on the number of impacts per POC for the impact and corresponding nonimpact microgenerators are shown, calculated using (7) at R_opt in the first and second cases.

Fig. 15.

Dependences of the maximum power on the number of collisions n for impact (1, 3) and their corresponding nonimpact (2, 4) microgenerators. (1, 2) First case; (3, 4) second case.

It can be seen that on a double logarithmic scale, these dependences also have the form of straight lines. In both cases, with increasing n the power of an impact microgenerator grows faster than that of a nonimpact one, and at n ≥ 2, the rate of energy transfer to the load in an impact microgenerator becomes greater than that of a nonimpact one. With the same n, the developed power in the first case, when the movable electrode initially comes into contact with the limiters located on the LWC, is greater than in the second case, when the movable electrode initially touches the limiters located on the RWC. The analysis shows that this is largely due to the greater energy consumption of the primary power source in the first case than in the second.

An equally important parameter characterizing the operation of the microgenerator is the ratio Kw of energy Wr, transferred to the load during the POC, to the energy Wv taken from the primary power source.

The dependences Kw on the number of impacts n per POC for the impact and corresponding nonimpact microgenerators, calculated at R_opt, are given in Fig. 16. With the increase in n for impact microgenerators, this ratio increases; moreover, in the first case, it is less than in the second case. At the same time, for nonimpact microgenerators, the value of the Wr/Wv ratio in the first and second cases is the same, and barely changes, but with n ≥ 2, it is less than for impact microgenerators.

Fig. 16.

Dependences of ratio Kw of energy Wr, transferred to the load during the oscillation period and to the energy Wv, taken from the primary power source, on the number of collisions n for impact (1, 3) and their corresponding nonimpact (2, 4) microgenerators. (1, 2) First case; (3, 4) second case.

Comparing Figs. 15 and 16, we see that the first case is preferable, since in this case the developed power is greater, and the slightly greater energy consumption is not significant, since the energy from the primary source is taken only once before starting the operation, while the energy is transferred to the load in every period. As a result, after several periods of operation, the energy transferred to the load becomes much greater than that taken from the primary source.

4 DISCUSSION

The studies of the three-electrode MEMT have shown that the motion of the movable electrode will be periodic only at certain ratios between the maximum interelectrode gap d₀ and amplitude of the casing’s oscillations A₀, and the dependence of the relation d₀/A₀ on the number of collisions n per POC in the interval 1 ≤ n < 20 is closely approximated by exponential functions of the form b₀n^b1.

With a constant height of the limiters, the maximum depth of capacitance modulation decreases with an increase in the number of collisions. If, simultaneously with a decrease in the d₀/A₀ ratio, there is a proportional reduction in the height of the limiters, then the maximum modulation depth of the capacitance of the MEMT will remain unchanged. To achieve the same number of collisions n in the first case, a larger d₀/A₀ ratio is required than in the second case.

The difference in the behavior of the movable electrode in the considered cases is due to the different initial position of the movable electrode relative to the stationary ones (with different initial conditions). In the first case, at the initial time t₀ = 0, the movable electrode at any n comes into contact with the limiters on the LWC, and with the beginning of the motion of the casing to the right, it begins to move, pushed by the LWC. Their joint motion at the same speed always continues until the speed of the casing reaches the value A₀ω. In the second case, the movable electrode at the initial moment comes into contact with the limiters on the RWC and starts moving only after the LWC has passed the distance d₀. Because d₀ depends on the number of collisions n, the initial coordinates and speed of the movable electrode in the second case depend on n.

In turn, the analysis of the operation of a microgenerator with a three-electrode MEMT showed that the dependences of the energy delivered to the load during the POC and the developed power on the load resistance have the maximum at R_opt. Moreover, with an increase in n, the value R_opt in the case of an impact microgenerator decreases faster than in the case of a nonimpact microgenerator. These dependences are also clearly described by exponential functions of the form b₀n^b1.

With the increase in n, the power of an impact microgenerator grows faster than that of a nonimpact one. Moreover, the dependences of the maximum power on the number of impacts during the period of oscillations of the casing of impact and the corresponding nonimpact generators are clearly described by exponential functions.

As n increases, the ratio of the energy Wr transferred to the load during the POC to the energy Wv taken from the primary power source, in the case of an impact microgenerator at R_opt, grows monotonically. At the same time, for the nonimpact microgenerator, it does not change. As a result, at n ≥ 2, an impact microgenerator converts the energy of the primary power source more efficiently than the corresponding nonimpact one.

In the case when the movable electrode initially touches the limiters located on the RWC, the microgenerator converts the energy received from the primary sources more efficiently, although it develops less power than in the case when the movable electrode initially comes into contact with the limiters located on the LWC.

Note that a microgenerator with a three-electrode MEMT generates an alternating voltage. However, since it does not draw charge from the primary power supply after the initial charge of the capacitors, potentially the period between maintenance of the primary power source when using a microgenerator of this type can be unlimited and is determined only by parasitic leaks.

CONCLUSIONS

The operation of microgenerators with a three-electrode MEMT in the impact periodic mode is analyzed for two extreme cases: (1) the movable electrode initially touches the limiters located on the LWC and (2) the movable electrode initially touches the limiters located on the RWC.

The necessary conditions for the implementation of the periodic impact mode of operation in the MEMT and the ratio of the parameters of the converter and the source of the external driving force are determined.

A comparison is made of the efficiency of the operation of the impact and corresponding nonimpact microgenerators.

It has been established that when using an impact converter, a gain in the developed power by 2–5 times is possible with a significant decrease by 1–2 orders of magnitude of the optimal load resistance compared to using the corresponding nonimpact converter.

It is shown that a microgenerator with a three-electrode MEMT, in the case when the movable electrode initially comes into contact with the limiters located on the LWC, develops more power than in the case when the movable electrode initially touches the limiters located on the RWC, even though it converts the energy received from primary sources less effective.

In general, the analysis carried out and the approach being developed make it possible to significantly narrow the range of the search for the necessary system parameters at the preliminary design stage and reduce the design time.