Spectrometric Determination of the Total Concentration of Single-Type Analytes Using Conventional Multidimensional Calibrations

Abstract

Multidimensional calibrations can be used for the spectrometric determination of the total concentration (c_Σ) of similar substances; these calibrations relate the generalized signals (A_Σ)_j measured at different wavelengths (λ_j) with the concentrations of these analytes (c_i) and their absorption coefficients (k_ij). Such calibrations are conventionally used for the separate determination of analytes, while the c_i values are calculated using chemometric algorithms. To find c_Σ, one should only take a sum of the found c_i values. Despite the simplicity of this type of group analysis, it is rarely used, and its capabilities have not been studied. It is unclear how the accuracy of the c_Σ estimate depends on the number of analytical wavelengths (AWLs), the number of standards, and other factors. The purpose of this study was to obtain relevant information using an example of model mixtures of arenes. The absorption spectra of arene mixtures were recorded in the region 230–280 nm, where these spectra are additive. We analyzed 55 hexane solutions containing three to six arenes with a total concentration of 0.1–0.5 mg/mL. The qualitative composition of the model mixtures was considered to compose the matrix of absorption coefficients of individual arenes. The c_i values were found by multiple linear regression (MLR, direct calibration). With a sufficiently large number of AWLs, the found c_i values were close to zero for arenes absent in the sample and close to the actual c_i values for the present arenes. The summation of the found c_i gave approximately correct estimates of c_Σ (±5%). The single errors of the group analysis were, as a rule, smaller than the errors of the determination of the mixture components. The complication of the model (the introduction of “extra” standards and an increase in the number of AWLs) did not affect the accuracy of the results of group analysis, and the simplification of the model increased errors. If only the most typical standards were used to form the model, the values of k_ij of which covered the entire range of possible values of k_ij, the presence of components in the sample that were not taken into account by the simplified model did not lead to a noticeable increase in errors.

The total concentration (c_Σ) of organic substances of a similar type is usually found by the spectrometric method without separating them; electrochemical methods, titrimetry, and gravimetry are also used for this purpose. In the course of an analysis, the generalized analytical signal A_Σ is measured, and the total index (TI), expressed in terms of a standard substance (X_st), is calculated from it. The calculated ICI value is an estimate of c_Σ. Examples include standard procedures for the spectrometric determination of hydrocarbons in waters or proteins in blood. Group analysis procedures based on TI measurements account for about 20% of all quantitative analysis techniques [1]. Unfortunately, the TI values can strongly and unpredictably differ from the actual values of c_Σ [2, 3]. The main sources of uncertainty are intragroup selectivity and nonadditivity of the analytical signals. In addition, analysts often make mistakes when forming a group of simultaneously determined substances, measuring A_Σ, or selecting Х_st [4]. The inaccuracy of determining total concentrations using the TI increases the interest of analysts in alternative methods of group analysis that do not require the expression of c_Σ in units of the X_st concentration (it is incorrect in metrological terms [1, 2]). In particular, c_Σ can be determined using linear multidimensional calibrations; examples are given in Table 1. The uncertainty of the results of group analysis is characterized in different ways, which makes it difficult to compare the corresponding procedurs.

Table 1. Examples of the spectrometric determinations of total concentrations (c_Σ) of similar analytes using multidimensional calibrations

The use of multidimensional calibration in spectrometric analysis involves multiwave measurements of generalized analytical signals and the calculation of the analysis results using chemometric algorithms. The popular PLS algorithm ensures a slightly higher calculation accuracy than other algorithms (all other things being equal), because the results are less affected by the sample components that are not included in the number of analytes [13]. However, PLS is more complex than other algorithms; it is implemented using less readily available software (the Unscrambler package) [14]. In this regard, many analysts prefer to use MLR or OLS algorithms, which can be implemented using the Excel package. Their use requires the preliminary formation of a matrix of the absorption coefficients of analytes at the selected AWLs. Matrix elements (k_ij values) are calculated from the absorption spectra of standard solutions of individual compounds (direct calibration) or from the absorption spectra of their model mixtures that make up the training sample (indirect calibration). In the latter case, an overdetermined system of linear equations of the form (A_Σ)_j = Σc_ik_ij is compiled and solved for unknown absorption coefficients by the least squares technique (OLS algorithm).

Let us distinguish two versions of determining c_Σ using linear multidimensional calibrations. Multidimensional calibrations of the first type (conventional calibrations) relate generalized signals of analytes (A_Σ)_j at different wavelengths (λ_j) with the concentrations of analytes (c_i) and their absorption coefficients (k_ij) at different wavelengths. Such calibrations are usually used to solve another problem, namely, for the separate spectrometric determination of the components of a mixture from its spectrum [13]. If a group analysis is required, it is necessary to calculate first the c_i values for all sample components belonging to the desired group using suitable chemometric algorithms and then take the sum of the found c_i values. This simple and metrologically correct version of group analysis ensures high accuracy in determining c_Σ, but it is rarely used [9, 10].

Multidimensional calibrations of the second type belong to the class of inverse calibrations. They relate the total concentrations of analytes of a similar type in model mixtures from the training set with their generalized signals measured at different AWLs, corresponding to the general equation c_Σ = Σb_jA_j. Using such calibrations, the matrix of absorption coefficients is not compiled, and the values of c_i are not calculated. Various chemometric algorithms are used, including PLS, to calculate c_Σ from the spectrum of a sample. The regression coefficients b_j are found in advance using a set of model mixtures of known composition. Features and analytical applications of multidimensional calibration of the second type are not considered in this article.

No generally accepted rules have yet been developed for constructing multidimensional calibration as applied to group spectrometric analysis of real samples. Single-component solutions of analytes of the desired group [5], calibration mixtures of the known composition prepared from them [5, 9–11], real samples for which the values of c_Σ were found by a reliable reference method [7], and even samples of unknown composition, characterized only by TI values [6, 8] are used as a source of initial data in the methods of group analysis. The metrological aspects of the determination of total concentrations using multidimensional calibration have almost been not studied. It is unclear how many mixtures should be included in the training set for constructing an indirect calibration. It is not known how many AWLs are needed to estimate c_Σ with the desired accuracy and how to choose them. The answers to these questions may be different for different types of calibrations. Because of the poor development of the methodology of group analysis, the necessary recommendations can be obtained only for special cases, generalizing the results of analyses of model mixtures of known compositions with different methods of processing the spectra. In this case, the components of the model mixtures must be of a similar type and stable compounds that absorb light in one region of the spectrum; absorption spectra of all mixtures should be recorded under identical conditions; deviations from additivity and the Bouguer–Lambert–Beer law are undesirable. These requirements are met by the absorption spectra of mixtures of monocyclic arenes.

The purpose of this study was to assess the analytical capabilities of multidimensional calibrations of the first (conventional) type on an example of determining the total concentration of monocyclic arenes in multicomponent hexane solutions by their light absorption in the UV spectral region.

EXPERIMENTAL

We used the following chemical reagents (cp grade): n-hexane (solvent), benzene (B), toluene (T), ethylbenzene (EB), o-xylene (o-X), p-xylene (p-X), and cumene (C). The stock solutions of the listed arenes were prepared by dissolving accurately weighed portions of them in hexane. The concentrations of the stock solutions were 1.5–2.0 mg/mL. Single-component working solutions were obtained by diluting stock solutions to concentrations 0.01–0.50 mg/mL. The absorption spectra of these solutions were used to calculate the specific absorption coefficients of the ith arene at the jth AWL (k_ij, cm²/mg). We used at least five working solutions with different concentrations of the ith arene; each solution was prepared at least three times; all the obtained k_ij values were averaged.

Multicomponent mixtures, that is, hexane solutions containing three to six monocyclic arenes, were prepared from the stock solutions. The total concentrations of arenes in these mixtures were in the range from 0.10 to 0.50 mg/mL; the ratio of the concentrations of different arenes in a single mixture did not exceed 10 : 1 (Table 2). A total of 55 model mixtures were prepared. Each solution was prepared at least three times.

Table 2.   Composition of some model mixtures of monocyclic arenes

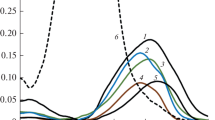
The absorption spectra of the prepared solutions were recorded with a step of 0.2 nm in the region 230–280 nm using an SF-2000-01 spectrophotometer in quartz cells with an optical path length of 1.0 cm against pure n-hexane. The absorption spectra of single-component solutions are given in [12]; the absorption spectra of some mixtures are shown in Fig. 1. Each spectrum was recorded 2–3 times; absorbance values were measured at the selected AWLs and averaged. In repeated measurements of the absorbance of one solution at a fixed AWL, the coefficients of variation (relative standard deviation, RSD) did not exceed 0.5%. Upon repeated preparation of solutions, the RSD values slightly increased but did not exceed 1%. To calculate k_ij, we selected the AWL values taken with a step of 0.2, 1, 2, 5, and 10 nm.

Fig. 1.

Absorption spectra of the model mixtures with different total concentrations of arenes: (1) mixture 9 (0.24 mg/mL), (2) mixture 1 (0.42 mg/mL), and (3) mixture 8 (0.35 mg/mL). The compositions of the mixtures are given in Table 2; the numbering of the mixtures is hereinafter retained.

An example can be provided by the specific absorption coefficients of six arenes at 11 AWLs, selected with a step of 5 nm (Table 3). The additivity of the absorbance of the mixtures was tested at different wavelengths. For this, the values of deviations from additivity (ΔA) taken in modulus were compared with the 3s test, characterizing the limit of random error in repeated measurements of the absorbance of a mixture at a given AWL. Deviations were considered statistically insignificant if ΔA ≤ 3s (Fig. 2).

Table 3. Matrix of the specific absorption coefficients (k_ij, cm²/mg) of six arenes at 11 AWLs

Fig. 2.

Examination of the additivity of light absorption of a six-component mixture of arenes (mixture 10).

To process the spectral data, the MLR method was used in the form of direct calibration, which was implemented using the author’s computer program Optic-MLR (MATLAB package). An advantage of this program compared to Microsoft Excel and other analogues is that it enables calculating the c_i values for several dozen mixtures at once, which shortens the time of analysis. The model, that is, the matrix of averaged k_ij values, was introduced into the program in advance. Before the analysis of the subsequent samples, a set of (A_Σ)_j values obtained for these mixtures was additionally introduced. The Optic MLR program results are the mass concentrations of those individual arenes for which k_ij values are entered into the program, that is, the concentration of the expected components of the test sample. The found concentrations $\left( {c_{i}^{*}} \right)$ were summed up, obtaining an analysis result $c_{\Sigma }^{*},$ approximately equal to the sought value c_Σ. The calculations were repeated using different sets of absorption coefficients (simplification or complication of the model) and changing the number of AWLs taken into account. The data were statistically processed according to the Student’s algorithm (n = 3, P = 0.95). The errors in determining the concentrations of individual arenes were calculated using the equation

$$\delta {{c}_{i}}\left( \% \right) = 100{\text{ }}(c_{i}^{*}-{{c}_{i}}){\text{/}}{{c}_{i}}.$$

(1)

The errors of the group analysis of single mixtures were calculated by the equation

$${{\delta }}{{c}_{\Sigma }}\left( \% \right) = 100(c_{\Sigma }^{*}-{{c}_{\Sigma }}){\text{/}}{{c}_{\Sigma }}.$$

(2)

The generalized error of the group analysis of different mixtures was characterized, as was customary in works on chemometrics, by the RMSEP parameter (root mean squared error of prediction) [5, 14], expressing this parameter in mg/mL,

$${\text{RMSEP}} = \sqrt {\frac{{\sum\limits_{q = 1}^{q = {\text{t}}} {{{{\left( {c_{q}^{{\text{*}}} - {{c}_{q}}} \right)}}^{2}}} }}{t}} ,$$

(3)

where t was the total number of analyzed mixtures (test sample size), $c_{q}^{{\text{*}}}$ and c_q were the found and actual total concentrations of arenes in the qth mixture (1 ≤ q ≤ t).

RESULTS AND DISCUSSION

Verification of the conditions necessary for constructing multidimensional calibration. It was necessary to examine whether the conditions enabling one to construct calibrations of the first type for hexane solutions of monocyclic arenes and use them for calculating total concentrations were satisfied. Verification has shown that all model compounds absorb UV radiation in the region 230–280 nm. In this wavelength region, there is no background, the calibration curves are straightforward, and the linear correlation coefficients are close to unity (r > 0.99); that is, in the studied concentration range, hexane solutions of arenes obey the Bouguer–Lambert–Beer law. Regardless of the nature of the arene and the selection of the AWL, changes in the concentration of single-component solutions had almost no effect on the specific absorption coefficient of a single arene (RSD < 3%). The absorption coefficients of different arenes are not proportional to each other and are quite different. The latter circumstance contributes to the accurate determination of the values of c_i.

Verification showed the statistical insignificance of deviations from additivity for the vast majority of the studied mixtures; deviations ΔA in modulus did not exceed the limiting value of random errors, that is, the 3s test (Fig. 2). We found small but statistically significant deviations from additivity only for several mixtures containing cumene and/or ethylbenzene, and such deviations were observed only in the 260–280 nm region. The appearance of minor deviations from additivity on individual AWLs does not interfere with the use of multidimensional calibrations of the first type in group analysis. However, in this case, the k_ij values should be calculated using mixtures of known compositions included in the training set.

Accuracy of the calculation of individual and total concentrations. The individual concentrations of six arenes present in the model mixtures were first calculated using the absorption coefficients of all arenes included in these mixtures (a six-component model). The number and nature of arenes present in a single sample were not taken into account in the calculations. For arenes absent in the mixture, c_i values close to zero were obtained. The individual concentrations of the arenes present were determined with rather large errors (δc_i < 70 rel %) (Table 4). The convergence of the results of calculating c_i for the reprepared mixtures was characterized by variation coefficients of the order 1–5% for components with concentrations of 0.07–0.2 mg/mL and 7–10% for components with concentrations lower than 0.07 mg/mL. The absolute errors (Δc_i) were both positive and negative. The summation of the c_i values usually led to a partial compensation of elementary errors. The modulus δc_Σ values were, as a rule, much less than the δc_i values. A similar pattern was observed in the group analysis of mixtures of carbohydrates [5] and polyphenols [9]. The revealed pattern does not contradict the well-known rules for calculating errors in indirect measurements [15]. These rules relate only to the summation of independent errors, and when all c_i are simultaneously calculated using the same multidimensional calibration, the elementary errors δc_i are not independent.

Table 4. Results and absolute errors of the spectrometric determination of individual arenes in six-component mixtures at 11 AWLs (MLR method)

It is known that the accuracy of determining c_i is affected by the number of the used AWLs [11, 13]. The number of AWLs should also affect the accuracy of determining total concentrations. Our experiments have confirmed this hypothesis. Thus, in measuring the absorbance of six-component mixtures with a step of 10 nm using six AWLs, we obtained errors (δc) reaching 40 rel % (modulo). This is to be expected because the system of linear equations describing the absorption of a single mixture is not overdetermined. Much better results (δc < 5%) were obtained when measuring in the same spectral region with a step of 5 nm using 11 AWLs. For 40 mixtures out of 55 analyzed, the error δc did not exceed 3%. A further increase in the number of AWLs did not lead to a decrease in errors (Table 5). A comparison of the RMSEP parameter values, which generally characterize errors in the analysis of mixtures, confirmed this conclusion. In using six AWLs, the RMSEP parameter was 0.075 mg/mL; 11 ADV gave 0.009 mg/mL, and 25, 50, and 250 AWLs resulted in 0.01, 0.015, and 0.016 mg/mL, respectively.

Table 5. Relative errors (δc, %) in determining the total concentration of arenes in model mixtures taking into account the absorption coefficients of six arenes

The total concentrations of arenes in three- and six-component mixtures under optimal conditions are determined with approximately equal accuracy (Table 4). The absence in the three-component mixtures of some of the six arenes, the absorption coefficients of which were used to construct the calibration, did not increase the error. “Extra” standards are quite admissible when constructing multidimensional calibrations of the first type.

Simplification of the model. The main problem of the spectrometric determination of analytes of a similar type in undivided mixtures is the lack of data on the number of components and the qualitative composition of the studied mixture. A precompiled matrix of absorption coefficients can be either excessive (containing substances absent in the samples and extra AWLs) or insufficient. The question arises whether it is possible to obtain correct estimates of c_Σ using simplified models that do not consider the absorption coefficients of some analytes of the desired group present in the test samples.

To answer this question, we determined the total concentration of arenes in six-component mixtures of different compositions using the specific absorption coefficients of only three arenes: benzene, ethylbenzene, and p-xylene. The selection of these very compounds for constructing a simplified model is explained by the differences in the values of the specific absorption coefficients of arenes in the region 250–270 nm (Table 3). Benzene has the smallest, p-xylene is the largest, and toluene, ethylbenzene, cumene, and o-xylene have intermediate values of these coefficients, similar to each other. It was decided to use one representative of each of the three subgroups (B, EB, and p-X) to construct a simplified calibration and perform calculations with the same AWLs as in the previous series of experiments. The calculation results for a simplified calibration are given in Table 6. A comparison of the data of Tables 5 and 6 led to the following conclusions:

Table 6. Relative errors (δc, %) in determining the total concentration of arenes in model mixtures taking into account the absorption coefficients of three arenes (B, EB, p-X)

(1) The simplification of the model, all other things being equal, deteriorates the accuracy of determining c_Σ. If the analysis of three-component mixtures using six standards and 11 AWLs leads to errors δc_Σ not exceeding 5% (Table 5), the analysis of the same mixtures using three standards increases δc_Σ to 10–15%;

(2) The presence of “extra” analytes in the samples, which were not taken into account when constructing a simplified calibration, does not necessarily lead to a decrease in the accuracy of the analysis. Otherwise, the analysis of six-component mixtures using a simplified calibration would give much larger errors than the analysis of three-component mixtures of B, EB, and p-X, which we did not observe;

(3) The accuracy of determining c_Σ from a simplified calibration slightly depends on the number of the used AWLs. For example, it was sufficient to measure the absorbance of the mixture at six AWLs to determine the total concentration of six different arenes using a three-dimensional calibration. A further increase in the number of AWLs did not lead to a decrease in the errors of the group analysis. Comparing the RMSEP values obtained for different numbers of AWLs (from 6 to 250) confirms this conclusion. In all cases, the RMSEP values were quite close to each other (0.015–0.025 mg/mL).

Thus, our experiment with model mixtures of monocyclic arenes showed that the multidimensional calibrations conventionally used for the separate determination of analytes of a similar type could be successfully used to assess the total concentration of the same analytes. Moreover, with the help of such calibrations, the total concentrations of analytes in their additive mixtures are determined more accurately than their individual concentrations.

Using the optimal number of AWLs and multidimensional calibrations of the first type, we quite accurately (±5%) determined the total concentration of monocyclic arenes in multicomponent model solutions. Solving the same problem by calculating the integral indicator leads to less accurate estimates of c_Σ (±7%), although this indicator was measured at the optimal AWL (250 nm) and expressed in terms of the optimal standard substance [12].

It is desirable to use multidimensional calibration of the first type to determine the total concentration of analytes in those samples where the number of the determined substances of a similar type is small, and their list is known in advance. An example is the analysis of synthetic drugs and dietary supplements. Calibrations of the first type can also be used if the composition of samples differs slightly from the list of standards used to construct multivariate calibration. The introduction of “extra” standards in the construction of the model does not lead to an increase in the errors of the group analysis (with the same AWL number). To improve the accuracy of the c_Σ estimate, it is desirable to form as complete a matrix of absorption coefficients as possible, including, if possible, data on all components of the sought group. This is crucial when the qualitative composition of analyte mixtures in the test samples is not fully known.

It is also possible to estimate the total concentration of analytes of a similar type using simplified models that include absorption coefficients of only some components of the desired group. Surely, the error in the results of the group analysis increases. Therefore, it is essential to include the most “typical” standards into the simplified model, selected so that the model covers the entire range of possible values of the absorption coefficients of the analytes of the desired group. This technique enabled us to obtain accurate results in the analysis of six-component mixtures using only three standards.

If the qualitative composition of the desired group is very complex and insufficiently studied, then the matrix of absorption coefficients cannot be compiled. In such cases, multidimensional calibration of the first type should not be used. In the course of group analysis, one can use multivariate calibration of the second type. Examples are provided by the determination of the total concentration of arenes in wastewater [12] or the total concentration of alkanes, cycloalkanes, and arenes in gasoline [7]. The analytical capabilities of multidimensional calibration of the second type will be considered in the next article.