INTRODUCTION

The formation of thin boundary films or interlayers plays an important role in many phenomena occurring at solid–gas and solid–liquid interfaces [1, 2]. A strong inhomogeneity inside such films leads to the development of a disjoining pressure [3–5]. In the case of curved film surfaces, the disjoining pressure acts as opposed to the capillary pressure [3, 6] and can be a very important factor for the heterogeneous formation of new phase particles [6–8]. However, in contrast to planar films or interlayers, the determination of the disjoining pressure is ambiguous in the case of curved interfaces [9]. The applicability of disjoining pressure isotherms of planar films is limited for films on wettable spherical solid particles with decreasing radii. The limits can be determined only by employing molecular models of the disjoining pressure. Moreover, it is of interest to use such models for studying the disjoining pressure of curved vapor interlayers around lyophobic solid particles, the data on which are to date insufficient.

This communication is devoted to studying the relations for the disjoining pressure of liquid films on lyophilic spherical solid particles and vapor interlayers on lyophobic ones within the gradient approximation of the classical density functional theory and to calculating and comparing disjoining pressures determined for such systems by thermodynamic and mechanical routes.

CALCULATION METHOD

The classical density functional theory [10, 11] is an efficient method for calculating the equilibrium structure of inhomogeneous fluid systems. Within the framework of this theory, grand thermodynamic potential \({{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]\) is specified as local number density functional of \(\rho \) of fluid molecules, while, in the bulk phase, this fluid may be in a vaporous or liquid state.

Below, we shall use the density functional theory under the gradient approximation [12–16] in combination with the Carnahan–Starling model for the contribution of solid spheres, as well as with the contribution of the mean field for long-range forces [17]. Accordingly, the grand thermodynamic potential of a one-component fluid with a liquid film or a vapor interlayer at a spherical solid particle of radius \({{R}_{{\text{p}}}}\) in preset volume \(V\) and at specified chemical potential \(\mu \) is determined [18–22] as

$$\begin{gathered} {{\Omega }^{{{\text{sf}}}}}\left[ \rho \right] = \int\limits_V {\left[ {{{k}_{{\text{B}}}}T\rho \left[ {\ln(\lambda _{{{\text{th}}}}^{3}\rho ) - 1 + \frac{{4\eta - 3{{\eta }^{2}}}}{{{{{(1 - \eta )}}^{2}}}}} \right.} \right]} \\ - \,\,\left. {a{{\rho }^{2}} + \frac{C}{2}{{{(\nabla \rho )}}^{2}} - \mu \rho + \rho {{w}_{{{\text{pf}}}}}} \right]d\vec {r}. \\ \end{gathered} $$
(1)

Here, \(\vec {r}\) is the radius vector directed from the center of the particle to a point of the system, \({{k}_{{\text{B}}}}\) is the Boltzmann constant, \(T\) is the absolute temperature of the system, \({{\lambda }_{{{\text{th}}}}} \equiv \hbar \sqrt {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {(m{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {(m{{k}_{{\text{B}}}}T}})} \) is the de Broglie thermal wavelength (\(\hbar \) is the Planck constant and \(m\) is the mass of a fluid molecule), \(\eta \equiv {{\pi {{d}^{3}}\rho } \mathord{\left/ {\vphantom {{\pi {{d}^{3}}\rho } 6}} \right. \kern-0em} 6}\) is the dimensionless molecular density of the fluid (\(d\) is the diameter of a molecule in the solid sphere model), \(a\) is the parameter of intermolecular attraction in the fluid within the mean field approximation, \(C = 14{{\sigma }^{5}}{{k}_{{\text{B}}}}T\) [23] is a parameter related to surface tension \(\gamma _{\infty }^{{}}\) at a planar interface between liquid and gas phases, \(\sigma \equiv {{\left( {{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}d,\) and \(\mu \) is the chemical potential of fluid molecules. The \({{w}_{{{\text{pf}}}}}\) value is the total potential of the interaction between a spherical solid particle (with molecule density \({{\rho }_{{\text{p}}}}\)) and a fluid molecule at point \(\vec {r}{\text{:}}\)

$$\begin{gathered} {{w}_{{{\text{pf}}}}} = \frac{{4\pi {{\varepsilon }_{{{\text{pf}}}}}{{\rho }_{{\text{p}}}}{{\sigma }^{3}}}}{5}\left\{ {\frac{\sigma }{{8r}}\left[ {\frac{{{{\sigma }^{8}}}}{{{{{(r + {{R}_{{\text{p}}}})}}^{8}}}} - \frac{{{{\sigma }^{8}}}}{{{{{(r - {{R}_{{\text{p}}}})}}^{8}}}}} \right.} \right. \\ + \,\,\left. {10{{\sigma }^{2}}\left( {\frac{1}{{{{{(r - {{R}_{{\text{p}}}})}}^{2}}}} - \frac{1}{{{{{(r + {{R}_{{\text{p}}}})}}^{2}}}}} \right)} \right] + \frac{5}{6}{{\sigma }^{3}} \\ \times \,\,\left( {\frac{1}{{{{{(r + {{R}_{{\text{p}}}})}}^{3}}}} - \frac{1}{{{{{(r - {{R}_{{\text{p}}}})}}^{3}}}}} \right) + \left. {\frac{{{{\sigma }^{9}}}}{9}{\kern 1pt} \left( {\frac{1}{{{{{(r - {{R}_{{\text{p}}}})}}^{9}}}} - \frac{1}{{{{{(r + {{R}_{{\text{p}}}})}}^{9}}}}} \right)} \right\}{\kern 1pt} , \\ \end{gathered} $$
(2)

where \({{\varepsilon }_{{{\text{pf}}}}}\) is the energy parameter of the Lennard-Jones interaction between a solid particle molecule and a fluid molecule.

The first step in solving the problem set in this communication is to find equilibrium fluid density profile \({{\rho }^{{{\text{(e)}}}}}\) from the stationary condition \({{\left. {{{\delta {{\Omega }^{{{\text{sf}}}}}} \mathord{\left/ {\vphantom {{\delta {{\Omega }^{{{\text{sf}}}}}} {\delta \rho }}} \right. \kern-0em} {\delta \rho }}} \right|}_{{{{{{\rho }}}^{{{\text{(e)}}}}}}}} = 0.\) Although the equilibrium density profiles may include nonspherical profiles corresponding to the formation of sessile droplets or bubbles [11], we shall, below, search only for spherically symmetric solutions with density \({{\rho }^{{{\text{(e)}}}}}\left( r \right),\) which describe the formation of concentric films or interlayers. Obviously, the existence of such solutions requires not only the sphericity of a solid particle, but also significant limitations imposed on its wettability or nonwettability, which are characterized in our model of potential \({{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]\) by dimensionless ratio \(\varepsilon \equiv {{4\pi {{\varepsilon }_{{{\text{pf}}}}}{{\rho }_{{\text{p}}}}{{\sigma }^{3}}} \mathord{\left/ {\vphantom {{4\pi {{\varepsilon }_{{{\text{pf}}}}}{{\rho }_{{\text{p}}}}{{\sigma }^{3}}} {5a\rho _{\infty }^{{\text{L}}}}}} \right. \kern-0em} {5a\rho _{\infty }^{{\text{L}}}}},\) where \(\rho _{\infty }^{{\text{L}}}\) is the number density of liquid molecules at \(\mu = {{\mu }_{\infty }}\) (\({{\mu }_{\infty }}\) is the chemical potential of fluid molecules under the condition of the equilibrium between liquid and vapor at a planar interface; hereinafter, subscript \(\infty \) characterizes the values determined at \({{\mu }_{\infty }}\)).

Substitution of Eq. (1) into the stationary condition gives nonlinear differential equation

$$\begin{gathered} \frac{C}{{{{k}_{{\text{B}}}}T}}\frac{1}{{{{r}^{2}}}}\frac{d}{{dr}}\left( {{{r}^{2}}\frac{{d{{\rho }^{{{\text{(e)}}}}}}}{{dr}}} \right) = \ln\left( {\lambda _{{{\text{th}}}}^{3}{{\rho }^{{{\text{(e)}}}}}} \right) + {{\eta }^{{{\text{(e)}}}}} \\ \times \,\,\left[ {\frac{{8 - 9{{\eta }^{{{\text{(e)}}}}} + 3{{\eta }^{{{\text{(e)}}}}}^{2}}}{{{{{\left( {1 - {{\eta }^{{{\text{(e)}}}}}} \right)}}^{3}}}}} \right] - \frac{{2a}}{{{{k}_{{\text{B}}}}T}}{{\rho }^{{{\text{(e)}}}}} - \frac{\mu }{{{{k}_{{\text{B}}}}T}} + \frac{{{{w}_{{{\text{pf}}}}}}}{{{{k}_{{\text{B}}}}T}} \\ \end{gathered} $$
(3)

with boundary conditions \({{\left. {{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \right|}_{{{{R}_{{\text{p}}}} + \delta }}} = 0\) and \({{\left. {{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \right|}_{{r \to \infty }}} = {{\rho }^{{{\text{G}}{\text{,L}}}}}\) [20–22] (\({{\rho }^{{\text{G}}}}\) and \({{\rho }^{{\text{L}}}}\) are the number densities of vapor and liquid molecules, respectively, at a preset value of chemical potential \(\mu \)). Hereinafter, the paired superscripts denote that the first and second superscripts refer to the cases of a liquid film and a vapor interlayer, respectively. The selection of point \({{R}_{{\text{p}}}} + \delta ,\) at which the boundary condition is imposed from the side of the solid particle, allows a certain arbitrariness. Account of the contribution from the solid spheres to the interaction potential makes impossible the approach of a molecule to a solid wall at a distance shorter than molecule radius \({d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2};\) therefore, choice of \(\delta = {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}\) is quite logical. However, any other choice of value \(0 \leqslant \delta \leqslant {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}\) must not noticeably change the solution to the problem. In our case, a specific choice of the \(\delta \) value will be determined by the numerical method for solving the problem.

At known equilibrium density profile \({{\rho }^{{{\text{(e)}}}}}\left( r \right)\), radius \({{R}_{{{\text{em}}}}}\) of the equimolecular dividing surface of a concentric liquid film or a vapor interlayer around a solid particle of radius \({{R}_{{\text{p}}}}\) is equal to [19–22]:

$$\begin{gathered} R_{{{\text{em}}}}^{3} = {{\left( {{{R}_{{\text{p}}}} + \delta } \right)}^{3}} + \frac{3}{{{{\rho }^{{{\text{L}}{\text{,G}}}}} - {{\rho }^{{{\text{G}}{\text{,L}}}}}}} \\ \times \,\,\int\limits_{{{R}_{{\text{p}}}} + \delta }^\infty {dr{{r}^{2}}({{\rho }^{{{\text{(e)}}}}}\left( r \right) - {{\rho }^{{{\text{G}}{\text{,L}}}}}){\kern 1pt} } . \\ \end{gathered} $$
(4)

The second step in solving the problem set in this communication is the search for the tangential and normal components of the pressure tensor from the found density profiles and thicknesses of the films or interlayers. In the spherically symmetric case, tangential component \({{p}_{{\text{T}}}}\) of the local pressure tensor in the system coincides with the integral density of the grand thermodynamic potential in Eq. (1) taken with the minus sign. Using the relation between normal \({{p}_{{\text{N}}}}\) and tangential \({{p}_{{\text{T}}}}\) components of the pressure tensor [24] (this relation follows from local condition of mechanical equilibrium \({{d\left( {{{p}_{{\text{N}}}}\left( r \right){{r}^{2}}} \right)} \mathord{\left/ {\vphantom {{d\left( {{{p}_{{\text{N}}}}\left( r \right){{r}^{2}}} \right)} {d{{r}^{2}}}}} \right. \kern-0em} {d{{r}^{2}}}}\) = \({{p}_{{\text{T}}}}\left( r \right)\)), we obtain

$${{p}_{{\text{N}}}}(r) = - \frac{2}{{{{r}^{2}}}}\int\limits_r^L {r{\kern 1pt} '{{p}_{{\text{T}}}}(r{\kern 1pt} ')dr{\kern 1pt} '} + \frac{{{{p}^{{{\text{L}}{\text{,G}}}}}{{L}^{2}}}}{{{{r}^{2}}}},$$
(5)

where \(L\) is the distance from the center of a solid particle, at which equality \({{p}_{{\text{N}}}}(L) = {{p}_{{\text{T}}}}(L) = {{p}^{{{\text{L}}{\text{,G}}}}}\) is fulfilled, and \({{p}^{{\text{G}}}}\) and \({{p}^{{\text{L}}}}\) are the bulk pressures of the vapor and liquid, respectively, at preset chemical potential \(\mu .\)

According to [25, 26], the condition of mechanical equilibrium for a spherical wetting liquid film or vapor interlayer on a spherical solid particle may be written as

$$\begin{gathered} {{p}^{{{\text{L}}{\text{,G}}}}}\left( \mu \right) = {{p}^{{{\text{G}}{\text{,L}}}}}\left( \mu \right) + \frac{{2{{\gamma }_{{{\text{em}}}}}}}{{{{R}_{{{\text{em}}}}}\left( \mu \right)}} - \\ - \,\,\left[ {{{p}_{{\text{N}}}}\left( {\mu ,{{r}_{i}}} \right) - {{p}^{{{\text{L}}{\text{,G}}}}}\left( \mu \right)} \right]{{\left( {\frac{{{{r}_{{\text{i}}}}}}{{{{R}_{{{\text{em}}}}}\left( \mu \right)}}} \right)}^{2}}, \\ \end{gathered} $$
(6)

where \(\gamma _{{{\text{em}}}}^{{}}\) is the surface tension for an equimolecular dividing surface; \({{R}_{{{\text{em}}}}}\) is the radius of the equimolecular dividing surface at a given chemical potential; and radius \({{r}_{{\text{i}}}}\) corresponds to the boundary near the solid surface, where the film or interlayer begins.

According to [27], grand thermodynamic potential \({{\Omega }^{{{\text{sf}}}}}\) of a system with a spherical liquid film or vapor interlayer may be represented in terms of thermodynamics as

$$\begin{gathered} {{\Omega }^{{{\text{sf}}}}} = - {{p}^{{{\text{L}}{\text{,G}}}}}\frac{{4\pi }}{3}\left( {R_{{{\text{em}}}}^{3} - R_{{\text{p}}}^{3}} \right) - {{p}^{{{\text{G}}{\text{,L}}}}}\left( {V - \frac{{4\pi }}{3}R_{{{\text{em}}}}^{3}} \right) \\ + \,\,4\pi R_{{{\text{em}}}}^{2}{{\gamma }_{{{\text{em}}}}} + {\kern 1pt} 4\pi R_{{\text{p}}}^{2}\int\limits_{{{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}}^\infty {dh\Pi \left( h \right)} , \\ \end{gathered} $$
(7)

where \(\Pi \left( h \right)\) has the meaning of the disjoining pressure determined thermodynamically for the film or interlayer. Equation (7) yields the equilibrium condition for the film or interlayer in the following form [27]:

$$\begin{gathered} {{p}^{{{\text{L}}{\text{,G}}}}}\left( \mu \right) = {{p}^{{{\text{G}}{\text{,L}}}}}\left( \mu \right) + \frac{{2{{\gamma }_{{{\text{em}}}}}}}{{{{R}_{{{\text{em}}}}}\left( \mu \right)}} \\ - \,\,{{\left( {\frac{{{{R}_{{\text{p}}}}}}{{{{R}_{{{\text{em}}}}}\left( \mu \right)}}} \right)}^{2}}\Pi \left( {{{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}} \right). \\ \end{gathered} $$
(8)

It is seen from Eqs. (6) and (8) that values

$${{\Pi }_{{\text{M}}}} \equiv \left[ {{{p}_{{\text{N}}}}\left( {\mu ,{{r}_{i}}} \right) - {{p}^{{{\text{L}}{\text{,G}}}}}\left( \mu \right)} \right]{{\left( {{{{{r}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{r}_{{\text{i}}}}} {{{R}_{{\text{p}}}}}}} \right. \kern-0em} {{{R}_{{\text{p}}}}}}} \right)}^{2}},$$
(9)
$${{{{\Pi }}}_{{\text{T}}}} = \left( {{{p}^{{{\text{G}}{\text{,L}}}}} - {{p}^{{{\text{L}}{\text{,G}}}}} + {{2{{\gamma }_{{{\text{em}}}}}} \mathord{\left/ {\vphantom {{2{{\gamma }_{{{\text{em}}}}}} {{{R}_{{{\text{em}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{em}}}}}}}} \right){{\left( {{{{{R}_{{{\text{em}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{em}}}}}} {{{R}_{{\text{p}}}}}}} \right. \kern-0em} {{{R}_{{\text{p}}}}}}} \right)}^{2}}$$
(10)

may be considered as the mechanical and thermodynamic definitions of the disjoining pressure for a spherical film or interlayer. Obviously, for liquid films and vapor interlayers, the equality \({{{{\Pi }}}_{{\text{M}}}} = {{{{\Pi }}}_{{\text{T}}}}\) must be fulfilled. If we take into account the constancy of the normal component of the pressure tensor at a planar interface, in the limiting case of a planar solid surface and a planar liquid film or vapor interlayer, both these definitions coincide with the well-known definition of the disjoining pressure [3, 4].

CALCULATION RESULTS

Equation (3) was solved at different values of chemical potential \(\mu \) by the shooting method using the Runge–Kutta method for solving the initial problem. Initial density values \({{\rho }^{{{\text{(e)}}}}}\left( L \right) = {{\rho }^{{{\text{G}}{\text{,L}}}}}\) were preset at rather large values of \(L\sim (20{\kern 1pt} - {\kern 1pt} 30)\sigma .\) Initial values of derivatives \({{\left. {{{d{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \mathord{\left/ {\vphantom {{d{{\rho }^{{{\text{(e)}}}}}\left( r \right)} {dr}}} \right. \kern-0em} {dr}}} \right|}_{{r = L}}}\) were selected in such a way that second boundary condition \({{\left. {{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \right|}_{{{{R}_{{\text{p}}}} + \delta }}} = 0\) was satisfied at \(0 \leqslant \delta \leqslant {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}.\) However, numerical solutions could not be obtained at too low values \(\delta \leqslant {d \mathord{\left/ {\vphantom {d 4}} \right. \kern-0em} 4}\) probably due to the limitations of the used method. To control the accuracy, the same profiles were calculated by “reverse shooting,” i.e., by solving the initial problem for \(r = {{R}_{{\text{p}}}} + \delta \) and the same values of \(\delta \) and \({{\rho }^{{{\text{(e)}}}}}\left( {{{R}_{{\text{p}}}} + \delta } \right),\) which were obtained previously. In fact, suitable values L were also chosen by preliminarily estimating the behavior of the solutions of the initial problem for Eq. (3) with corresponding initial conditions at \(r \approx {{R}_{{\text{p}}}} + {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}.\)

The following values of the parameters were taken: \(T = 90\) K, πd 3/6 = 16.22 × 10–30 m3, σ = (πd 3/6)1/3 = 2.53 × 10–10 m, and a = 3.58 × 10–49 J m3, with the following values corresponding to them μ∞ = –1.539 × 10–20 J, \(\eta _{\infty }^{{\text{L}}} = {{\sigma }^{3}}{{\rho }^{{\text{L}}}}\left( {{{\mu }_{\infty }}} \right) = 0.408,\) \(\eta _{\infty }^{{\text{G}}} = {{\sigma }^{3}}{{\rho }^{{\text{G}}}}\left( {{{\mu }_{\infty }}} \right) = 0.00296,\) \({{\gamma }_{\infty }} = 0.0119\) N/m, and \({{R}_{{\text{p}}}} = 10\sigma .\) When a liquid film was formed, the following parameters were used ρp = 26.6 × 1027 m–3 (as for quartz), \({{\varepsilon }_{{{\text{pf}}}}} = 5{{{a \mathord{\left/ {\vphantom {a \sigma }} \right. \kern-0em} \sigma }}^{3}}\), and \(\mu > {{\mu }_{\infty }}\) (metastable supersaturated vapor). In the case of a vapor interlayer, we used ρp = 1.07 × 1027 m–3 (as for paraffin), \({{\varepsilon }_{{{\text{pf}}}}} = {{{{0.01a} \mathord{\left/ {\vphantom {{0.01a} \sigma }} \right. \kern-0em} \sigma }}^{3}}\), and \(\mu < {{\mu }_{\infty }}\) (metastable extended liquid).

Figure 1 shows found dimensionless equilibrium density profiles \({{\eta }^{{{\text{(e)}}}}}\left( r \right) \equiv {{\pi {{d}^{3}}{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \mathord{\left/ {\vphantom {{\pi {{d}^{3}}{{\rho }^{{{\text{(e)}}}}}\left( r \right)} 6}} \right. \kern-0em} 6}\) as depending on \({{\tilde {r} \equiv r} \mathord{\left/ {\vphantom {{\tilde {r} \equiv r} \sigma }} \right. \kern-0em} \sigma }\) at the values of dimensionless shift of the chemical potential indicated in the figure field \(b \equiv {{\left( {\mu - {{\mu }_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {\mu - {{\mu }_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}.\) It can be seen that solutions of Eq. (3) corresponding to concentric films and interlayers do exist for the selected values of the parameters. Moreover, the calculations have shown that, at \({{\mu }_{\infty }} < \mu < \mu _{{{\text{th}}}}^{{\text{G}}}\) in the case of liquid films and at \(\mu _{{{\text{th}}}}^{{\text{L}}} < \mu < {{\mu }_{\infty }}\) in the case of vapor interlayers, there are two such solutions for each value of \(\mu .\) Therewith, the first of them corresponds to a stable equilibrium profile (local minimum of functional \({{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]\) in profile space \(\rho \)), while the second one, refers to an unstable equilibrium profile (saddle point of functional \({{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]\) in profile space \(\rho \)). A similar situation is well known for nucleation on charged particles [28–31]. In the case of the formation of droplets on wettable condensation nuclei, similar behavior was related earlier to the isotherms of disjoining pressure in liquid films [7, 8]. It is obvious that droplets and vapor interlayers, in which the density profiles correspond to minimum \({{\Omega }^{{{\text{sf}}}}},\) will be long-living.

Fig. 1.
figure 1

Calculated dimensionless \({{\eta }^{{{\text{(e)}}}}}\left( r \right) = {{\sigma }^{3}}{{\rho }^{{{\text{(e)}}}}}\left( r \right)\) profiles of equilibrium density as functions of the distance from the center of a solid particle at the indicated values of dimensionless shift of the chemical potential b: for (a) liquid films in a supersaturated vapor and (b) vapor interlayers in an extended liquid. The horizontal dotted lines indicate the densities of the bulk gas and liquid phases. The vertical dashed lines show the radii of stable (\(\tilde {R}_{{{\text{em}}}}^{{{\text{st}}}} \equiv {{R_{{{\text{em}}}}^{{{\text{st}}}}} \mathord{\left/ {\vphantom {{R_{{{\text{em}}}}^{{{\text{st}}}}} \sigma }} \right. \kern-0em} \sigma }\)) and unstable (critical, \(\tilde {R}_{{{\text{em}}}}^{{{\text{cr}}}} \equiv {{R_{{{\text{em}}}}^{{{\text{cr}}}}} \mathord{\left/ {\vphantom {{R_{{{\text{em}}}}^{{{\text{cr}}}}} \sigma }} \right. \kern-0em} \sigma }\)) liquid films and vapor interlayers.

Full size image

Note that the threshold \(\mu _{{{\text{th}}}}^{{\text{G}}}\) and \(\mu _{{{\text{th}}}}^{{\text{L}}}\) values depend on the particle radius and other parameters of a system. At the parameters taken to plot Fig. 1, we have \({{b_{{{\text{th}}}}^{{\text{G}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{G}}} - {{\mu }_{\infty }}} \right)} \mathord{\left/ {\vphantom {{b_{{{\text{th}}}}^{{\text{G}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{G}}} - {{\mu }_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}\) = 0.127 and \({{b_{{{\text{th}}}}^{{\text{L}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{L}}} - {{\mu }_{\infty }}} \right)} \mathord{\left/ {\vphantom {{b_{{{\text{th}}}}^{{\text{L}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{L}}} - {{\mu }_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}\) = –0.233. The existence of a peak in the density profile of a liquid film near the surface of a solid particle in Fig. 1a shows that taken value \({{\varepsilon }_{{{\text{pf}}}}} = 5{{{a \mathord{\left/ {\vphantom {a \sigma }} \right. \kern-0em} \sigma }}^{3}}\) does correspond to good wetting of the solid particle substance by the liquid phase. Accordingly, the choice of \({{\varepsilon }_{{{\text{pf}}}}} = {{{{0.01a} \mathord{\left/ {\vphantom {{0.01a} \sigma }} \right. \kern-0em} \sigma }}^{3}}\) must, with a reserve, ensure the lyophobicity of the solid particle. As parameter \({{\varepsilon }_{{{\text{pf}}}}}\) decreases for a supersaturated vapor and increases in the case of an extended liquid, the equilibrium solutions of Eq. (3) in the form of concentric density profiles disappear. Apparently [11], a transition to solutions in the form of sessile droplets or bubbles occurs in this case.

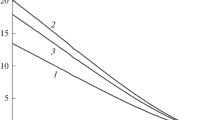
The calculated density profiles were substituted into the relation for \({{p}_{{\text{T}}}}(r)\) that follows from Eq. (1) and, then, into Eq. (5) for \({{p}_{{\text{N}}}}(r).\) The results of resulting profiles of tangential pT(r) and normal component \({{p}_{{\text{N}}}}(r)\) of the pressure tensor are shown in Fig. 2.

Fig. 2.
figure 2

Dependences of dimensionless tangential \({{{{{\tilde {p}}}_{{\text{T}}}} \equiv {{p}_{{\text{T}}}}{{\sigma }^{3}}} \mathord{\left/ {\vphantom {{{{{\tilde {p}}}_{{\text{T}}}} \equiv {{p}_{{\text{T}}}}{{\sigma }^{3}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}\) and normal \({{{{{\tilde {p}}}_{{\text{N}}}} \equiv {{p}_{{\text{N}}}}{{\sigma }^{3}}} \mathord{\left/ {\vphantom {{{{{\tilde {p}}}_{{\text{N}}}} \equiv {{p}_{{\text{N}}}}{{\sigma }^{3}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}\) components of the pressure tensor on the distance from the center of a solid particle at the indicated values of the dimensionless shift of the chemical potential b in (a) liquid films in a supersaturated vapor and (b) vapor interlayers in an extended liquid. The horizontal dotted lines indicate the pressures in the bulk gas and liquid phases. The vertical dashed lines show the values of the radii of stable (\(\tilde {R}_{{{\text{em}}}}^{{{\text{st}}}} \equiv {{R_{{{\text{em}}}}^{{{\text{st}}}}} \mathord{\left/ {\vphantom {{R_{{{\text{em}}}}^{{{\text{st}}}}} \sigma }} \right. \kern-0em} \sigma }\)) and unstable (critical, \(\tilde {R}_{{{\text{em}}}}^{{{\text{cr}}}} \equiv {{R_{{{\text{em}}}}^{{{\text{cr}}}}} \mathord{\left/ {\vphantom {{R_{{{\text{em}}}}^{{{\text{cr}}}}} \sigma }} \right. \kern-0em} \sigma }\)) liquid films and vapor interlayers and positions (\(\tilde {r}_{{\text{i}}}^{{{\text{st}}}} \equiv {{r_{{\text{i}}}^{{{\text{st}}}}} \mathord{\left/ {\vphantom {{r_{{\text{i}}}^{{{\text{st}}}}} \sigma }} \right. \kern-0em} \sigma }\) and \(\tilde {r}_{{\text{i}}}^{{{\text{cr}}}} = {{r_{{\text{i}}}^{{{\text{cr}}}}} \mathord{\left/ {\vphantom {{r_{{\text{i}}}^{{{\text{cr}}}}} \sigma }} \right. \kern-0em} \sigma }\)) of pN maxima in them.

Full size image

It follows from Fig. 2 that it is reasonable to choose the position of the maximum in the normal component of the pressure tensor as radius \({{r}_{{\text{i}}}}\) of a film or interlayer boundary near a solid surface. Figure 2a suggests that, in a droplet concentric with a particle, the maximum of the normal pressure component is located at some distance from the particle surface closer to the middle of the film, and, at point \({{r}_{{\text{i}}}}\), the values of \({{p}_{{\text{N}}}}\) and \({{p}_{{\text{T}}}}\) are very close to each other, while Fig. 2b indicates that, in the case of a vapor interlayer, the maximum of the disjoining pressure is reached at \({{r}_{{\text{i}}}} = {{R}_{{\text{p}}}} + \delta ,\) with the values of \({{p}_{{\text{N}}}}\) and \({{p}_{{\text{T}}}}\) differing significantly. This difference may be explained by the fact that, in the case of a droplet on a lyophilic particle, the surface forces at the liquid–particle and liquid–vapor interfaces have approximately the same radius of action; therefore, the region of overlapping surface layers is located approximately in the middle of the film. In the case of a vapor interlayer on a lyophobic particle, the properties of the interlayer most strongly differ from the properties of the liquid namely near the particle surface.

With an increase in the deviation of the chemical potential from \({{\mu }_{\infty }}\), thicknesses \({{h}_{{{\text{em}}}}} \equiv {{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}\) of a liquid film (at \(\mu > {{\mu }_{\infty }}\)) and a vapor interlayer (at \(\mu < {{\mu }_{\infty }}\)) increase, and the maximum value of the normal component of the pressure tensor increases as well. As the hydrophilicity rises (with increasing parameter \({{\varepsilon }_{{{\text{pf}}}}}\)), the maximum of \({{p}_{{\text{N}}}}(r)\) grows in a liquid film. In a vapor interlayer, the maximum of \({{p}_{{\text{N}}}}(r)\) increases with increasing hydrophobicity (decreasing \({{\varepsilon }_{{{\text{pf}}}}}\)).

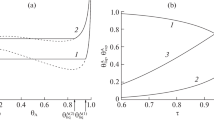
To calculate the mechanical disjoining pressure, let us introduce the \({{r}_{{\text{i}}}},\) \(\max {{p}_{{\text{N}}}}\left( r \right),\) \({{p}^{{\text{L}}}},\) and \({{p}^{{\text{G}}}}\) values corresponding to the films and interlayers into the relation for \({{\Pi }_{{\text{M}}}}\) and substitute the values of \({{R}_{{{\text{em}}}}}\) previously found using Eq. (4) into it. The calculation results obtained at four radii \({{R}_{{\text{p}}}}\) of the central solid particle are presented in the main field of Fig. 3. Largest radius \({{R}_{{\text{p}}}} = 60\sigma \) practically corresponds to the limiting case of a planar solid wall.

Fig. 3.
figure 3

Dependences of dimensionless disjoining pressure \({{{{{\tilde {\Pi }}}_{{\text{T}}}} \equiv {{\Pi }_{{\text{T}}}}{{\sigma }^{3}}} \mathord{\left/ {\vphantom {{{{{\tilde {\Pi }}}_{{\text{T}}}} \equiv {{\Pi }_{{\text{T}}}}{{\sigma }^{3}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}\) on thickness \({{\tilde {h}}_{{{\text{em}}}}} \equiv {{\tilde {R}}_{{{\text{em}}}}} - {{\tilde {R}}_{{\text{p}}}}\) at different radii of solid particles: in (a) spherical liquid films in a supersaturated vapor and (b) spherical vapor interlayers in an extended liquid.

Full size image

When calculating the thermodynamic disjoining pressure for liquid films, we use an iteration procedure. At the first step, we calculate \({{{{\Pi }}}_{{\text{T}}}}\) by Eq. (10) at \({{\gamma }_{{{\text{em}}}}} = {{\gamma }_{\infty }}.\) In the case of droplets, the presence of the impermeable surface of a condensation nucleus significantly affects the fluid density near this surface, as is seen from the peak in Fig. 1a. This influence is even more pronounced for the normal and tangential components of the tensor near the surface of the solid nucleus. Let us exclude the contribution related to the presence of the foreign particle and the surrounding solvation shell and integrate grand thermodynamic potential \({{\Omega }^{{{\text{sf}}}}}\) starting from radius \({{r}_{{\text{i}}}}\) rather than over total volume V. The elimination of the region of integration from \({{R}_{{\text{p}}}}\) to \({{r}_{{\text{i}}}}\) for \({{\Omega }^{{{\text{sf}}}}}\) in the left-hang side of Eq. (7) leads to the replacement of radius \({{R}_{{\text{p}}}}\) by \({{r}_{{\text{i}}}}\) in the first term of its right-hand side. We substitute the resulting \({{\Pi }}_{{\text{T}}}^{{(0)}}(h)\) dependence into expression (7) to obtain the value of \(\gamma _{{{\text{em}}}}^{{(1)}}.\) Then, we substitute \(\gamma _{{{\text{em}}}}^{{(1)}}\) into Eq. (10) and, again, find the \({{\Pi }}_{{\text{T}}}^{{(1)}}(h)\) dependence. The inset in Fig. 3a shows the second iteration of \({{\Pi }}_{{\text{T}}}^{{(2)}}(h).\) The calculation has shown that the result of the iterations converges rather rapidly.

To calculate the thermodynamically defined disjoining pressure of a vapor interlayer on a lyophobic particle, we exclude term \({{2{{\gamma }_{{{\text{em}}}}}} \mathord{\left/ {\vphantom {{2{{\gamma }_{{{\text{em}}}}}} {{{R}_{{{\text{em}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{em}}}}}}}\) from the equation for \({{{{\Pi }}}_{{\text{T}}}}\) using relation (7). As a result, we obtain the following integral equation for \({{{{\Pi }}}_{{\text{T}}}}{\text{:}}\)

$${{{{\Pi }}}_{{\text{T}}}}\left( {{{h}_{{{\text{em}}}}}} \right) = q\left( {{{R}_{{{\text{em}}}}}} \right) - \frac{2}{{{{R}_{{{\text{em}}}}}}}\int\limits_{{{h}_{{{\text{em}}}}}}^\infty {dh{{\Pi }_{{\text{T}}}}\left( h \right)} ,$$
(11)

where \({{h}_{{{\text{em}}}}} \equiv {{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}\) is the thickness of the spherical interlayer and

$$\begin{gathered} q\left( {{{R}_{{{\text{em}}}}}} \right) \equiv \left[ {\frac{{{{p}^{{{\text{G}}{\text{,L}}}}}R_{{{\text{em}}}}^{2}}}{{3R_{{\text{p}}}^{2}}} - \frac{{{{p}^{{{\text{L}}{\text{,G}}}}}}}{3}\left( {\frac{{R_{{{\text{em}}}}^{2}}}{{R_{{\text{p}}}^{2}}} + \frac{{2{{R}_{p}}}}{{{{R}_{{{\text{em}}}}}}}} \right)} \right] \\ + \,\,\frac{{\left( {{{\Omega }^{{{\text{sf}}}}} + {{p}^{{{\text{G}}{\text{,L}}}}}V} \right)}}{{2\pi {{R}_{{{\text{em}}}}}R_{{\text{p}}}^{2}}}. \\ \end{gathered} $$
(12)

For each value of \({{R}_{{{\text{em}}}}}\), the \(q({{R}_{{{\text{em}}}}})\) function can be calculated point-by-point. Equation (11) can be solved by reducing it to an ordinary differential equation by multiplying both its sides by \({{R}_{{{\text{em}}}}}\) and differentiating over \({{h}_{{{\text{em}}}}}.\) The solution results and the comparison of the \({{{{\Pi }}}_{{\text{T}}}}\) and \({{\Pi }_{{\text{M}}}}\) dependences on thickness \({{h}_{{{\text{em}}}}} = {{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}\) in the cases of the formation of interlayer are illustrated in the inset of Fig. 3b.

As follows from Figs. 3a and 3b, the disjoining pressure in a spherical concentric droplet around a lyophilic particle decreases, while, in a concentric bubble on a lyophobic particle the disjoining pressure, increases with decreasing radius of the lyophobic particle. Accordingly, the disjoining pressure in a planar liquid film of a preset thickness has the highest possible value at a given lyophilicity of a solid particle, while, in a planar vapor layer, it is the lowest at a given lyophobicity of a particle. The agreement between the mechanical and thermodynamic definitions of the disjoining pressure for spherical films and interlayers is rather good.

CONCLUSIONS

Using unified approach, we have shown that the gradient approximation of the classical density functional theory makes it possible to explicitly calculate the equilibrium local density profiles, the components of the pressure tensor, and the thicknesses of thin concentric interlayers between a lyophilic or lyophobic solid surface and a gas or liquid phase, respectively. These interlayers are not isotropic, and there is a disjoining pressure in them. Dependences of this pressure on the interlayer thickness have been obtained. In the presence of a capillary pressure inside the interlayers, the disjoining pressure counteracts it and leads to the appearance of stable long-living droplets around lyophilic solid particles and bubbles around lyophobic particles. It has been shown that the mechanical and thermodynamic definitions of the disjoining pressure in a spherical interlayer agree with each other.