INTRODUCTION

Many products and structures in mechanical engineering are obtained using welded joints. It is well known that the heat affected zone (HAZ) is heterogeneous and has different structure when moving away from the weld (zone of partial melting, overheating, normalizing, incomplete regrowth, and recrystallization). At the same time, there is a considerable gradient in the physical and mechanical characteristics of the material [1]. When the welded material is heated to temperatures of 1100–1450°C, an overheated area is formed that is characterized by a considerable grain growth [2]. The grain size in the overheated zone may differ from the initial grain size of the material being welded up to 16 times. Such structural changes reduce the mechanical properties of steel, especially plasticity and resistance to dynamic loading. Thus, the coarse-grained section of the HAZ is the most weakened spot in welded structures, where failure occurs most often. In this regard, during the operation of welded products and structures, it is necessary to have data on the actual condition of the material and its residual resource in various sections of the HAZ.

A large number of parts of mechanisms and structures operate under cyclic loading conditions [3–5]. Statistics show that approximately 80% of all breakdowns and accidents are associated with the fatigue nature of material failure [5, 6]. The process of fatigue failure is complicated and depends on the structural state of metal, its strength properties, the scheme and frequency of loading, etc. Currently, the processes of fatigue failure of HAZ at various distances from the weld are poorly studied.

It is well known that the nucleation and development of cracks begins in a surface layer of material in the parts [3, 7]. Therefore, it is of particular interest to study the structure of metal on its surface and assess the degree of its degradation during operation before the occurrence of a macrocrack.

The approaches of fractal representations can be applied to study structural changes in metallic material, and these are currently widely used in metal science [8–11]. The fractal dimension index of a microstructure reflects the processes of accumulation of structural damage to material and can be used to assess its residual resource [9–11].

However, the use of methods of optical observation of hazardous (according to the stress-strain state scheme) zones in the structure is not always possible; this requires the development and application of additional methods of nondestructive diagnostics. Acoustic echo method is one of the most promising structurally sensitive methods for analyzing metallic materials [12, 13]. This is explained by the fact that the parameters of elastic waves (velocity, attenuation, waveform, and pulse energy) react to structural processes occurring in the tested medium and depend on its density and elastic modulus, the size and geometry of structural inhomogeneities, and other characteristics of the medium under study [14, 15]. The formation of a crystallographic texture also leads to anisotropy of the physical and mechanical properties of metal, including elastic ones.

Thus, the purpose of this study is to evaluate the processes of degradation of the steel structure during fatigue failure of various sections of the welded joint using approaches of digital image processing of microstructures, fractal analysis, and ultrasonic testing.

MATERIALS AND METHODS

St3 steel, widely used for the manufacture of welded structures in general mechanical engineering, was chosen as a material for the study of the process of fatigue failure of welded joints in various sections of the HAZ. The chemical composition and mechanical properties of the material under study are listed in Tables 1 and 2, respectively.

Table 1. Chemical composition of steel St3, %
Full size table
Table 2. Mechanical properties of St3 steel
Full size table

Butt welded joints of two plates with a square cross section of 30 × 30 mm were made to prepare experimental samples for fatigue testing. The weld was made in several passes by manual arc welding in accordance with GOST (State Standard) 5264-80 (Fig. 1). At the same time, welding modes were selected that provide a HAZ of at least 15 mm.

Fig. 1.
figure 1

Scheme of welding and cutting samples from the sections of heat affected zone.

Full size image

Fatigue test samples are made from blanks cut along the weld at different distances from the fusion zone. The samples were cut from two sections of the HAZ, namely from the overheated (coarse grain) and normalizing (fine grain) zones, as well as from the main material (for comparative tests).

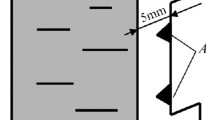
Fatigue tests of the samples were carried out on samples with a thickness of 3 mm and a working area of 60 × 15 mm (Fig. 2). The roughness of the samples in the working area was Ra = 0.4 (achieved by repeated polishing). Fatigue samples were loaded according to the cantilever bending scheme (Fig. 2a, cycle asymmetry coefficient R = –l). The tests were carried out taking into account the requirements of GOST (State Standard) 25.502-79. The frequency of elastic-plastic cyclic deformation was set equal to 8.3 Hz (500 cycles/min) using a frequency converter. The loading amplitude during fatigue tests was selected based on the obtained mechanical properties of the material under study and corresponded to the range of 220–290 MPa.

Fig. 2.
figure 2

Fatigue testing unit (a) and a sample with sections for optical and ultrasonic testing (b); 1, 2, and 3 tested sections.

Full size image

The study of structural changes and the evaluation of acoustic parameters in the process of elastic-plastic cyclic loading was carried out in the area with the highest stresses according to the stress-strain state design scheme in three zones (according to the width of the section under study, see Fig. 2b) with the width of each zone of 5 mm. Marks were made on the tested surfaces of a sample to increase the accuracy of sensor positioning.

After each operating interval, elastic wave propagation velocities were measured at the microstructure testing point,

$${{C}_{i}} = \frac{{2h}}{{{{\tau }_{i}}}},$$
(1)

where h is the sample wall thickness and τi is the propagation time of ultrasonic pulses.

The measurements were carried out at a temperature of 20°C in the emission–reception mode (elastic waves are emitted and received by one sensor), therefore, in formula (1) the path was assumed to be equal to 2h.

To measure the propagation velocities of ultrasonic pulses, the ASTRON spectral acoustic measuring and computing complex (MCC) was used [15] that provides measurement of the propagation time of acoustic pulses in the material with an accuracy of 2 × 10–9 s. Transverse and longitudinal waves with a frequency of 5 MHz were used in measurements.

For the practical application of acoustic methods for assessing the degree of structural degradation, we used the acoustic diagnostic parameter Ds,

$${{D}_{{\text{s}}}} = \frac{{C_{t}^{{||}} + C_{t}^{ \bot }}}{{{{C}_{l}}}},$$
(2)

where \(C_{t}^{{||}}\), m/s is the velocity of an elastic shear wave pulse with transverse polarization (the direction of polarization along the sample), \(C_{t}^{ \bot }\), m/s is the velocity of an elastic shear wave pulse with transverse polarization (the direction of polarization across the sample), and Cl, m/s is the velocity of an elastic longitudinal wave pulse.

Each sample was loaded in stages. Ultrasonic and microstructural studies, as well as microhardness assessment were carried out before the test and after each stage of cyclic deformation up to the formation of a macrocrack. After the macrocrack has been formed, the features of its propagation and growth under further loading were evaluated.

The study of the microstructure of steel was carried out using a KYENCE VHX-1000 optical metallographic microscope having previously etched the polished surface with a 4% HNO3 solution and protecting the tested area for the duration of fatigue tests.

To determine magnetic characteristics, an MA-412MM magnetic analyzer was used that allows determining the values of coercive force (Hc). The measurement base, corresponding to the distance between the contact pads, was 30 mm. Measurements were carried out at least 5 times with precise geometric reference to the studied area.

The study of microhardness was carried out in the zone of maximum stresses using an ITV-1-AM microhardness meter under a load of 1 kgf.

For preliminary processing and evaluation of the fractal dimension of microstructure images (Df) as well as calculation of the quantitative indices of slip bands, a program was developed in the Matlab environment [16–18].

The fractal dimension of the material structure was calculated after preliminary processing of microstructure photographs. Preprocessing of a microstructure image included sharpening, brightness equalization, filtering (including using a wavelet filter), and binarization. These processing operations are the most effective tools for processing images of metal microstructures [17, 18].

The resulting image of the microstructure was subjected to a two-dimensional wavelet transform. This makes it possible to more clearly identify the boundaries of the metal structure, increase the accuracy of the fractal dimension calculation, eliminate the influence of a subjective factor on the result, and automate the calculation process.

To calculate the fractal dimension (Df), the microstructure image was covered with a rectangular grid with cell size e. The range of cell sizes depended on the average metal grain size (d) and varied from 0.01d to d. After that, the number of cells (Nε) containing the boundary was calculated. The fractal dimension was calculated by the formula

$$\log ({{N}_{\varepsilon }}) = {{D}_{f}}\log (1{\text{/}}e) + C,$$
(3)

where Df  is the fractal dimension and C is the regression curve coefficient.

In addition to the index Df, several quantitative indicators were also used to quantify structural changes. To do this, the photos of the microstructure were shifted and rotated relative to the initial image corresponding to the initial material state. The offset and rotation with a step of 1 pixel were carried out until the maximum contrast of the current image with the original one was achieved. To identify structural changes, an array of binarized images corresponding to different numbers of cycles was subtracted from the data array corresponding to the initial material state. After that, the concentration of slip bands and defects in the material (n) was calculated using the Matlab functional according to the following dependence:

$$n = \frac{{{{N}_{{{\text{def}}}}}}}{{{{S}_{{{\text{im}}}}}}},\;{\text{m}}{{{\text{m}}}^{{ - 2}}},$$
(4)

where Ndef is the number of slip bands and defects on the analyzed microstructure image and Sim is the area of the analyzed microstructure image, mm2.

Also, the fraction (Srel) of microstructure defects and slip bands formed during cyclic loading was determined after preprocessing according to the following dependence:

$${{S}_{{{\text{rel}}}}} = \frac{{{{S}_{{{\text{def}}}}}}}{{{{S}_{{{\text{im}}}}}}} \times 100\% ,$$
(5)

where Sdef is the area occupied by slip bands and defects in the analyzed microstructure image, mm2.

The spread of experimental data was estimated based on statistical processing of the results of calculating the indicated parameters in several images (up to 16 images for each analyzed point) in the maximum stress zone (see Fig. 2a).

RESULTS AND DISCUSSION

The initial microstructure of the working area of samples cut from various sections of the St3 welded joint as well as from a section of the main material is shown in Fig. 3.

Fig. 3.
figure 3

Initial microstructures of samples cut from the overheating (a) and normalizing (b) sites of heat affected zone during welding and from the main material (c) of St3 steel.

Full size image

The microstructure of St3 steel in the studied sections of the heat affected zone is represented by a ferrite–pearlite structure. The average grain size at the overheated site of the heat affected zone was approximately 45 μm and at the normalization site, approximately 10 μm. A high degree of heterogeneity was also observed in all areas of the heat affected zone.

The evolution of the microstructure of the overheating and normalizing sites of St3 steel during fatigue tests with the stress amplitude in the cycle of σmax = 250 MPa (close to the conditional yield strength, see Table 2) is shown in Figs. 4a and 4b for different sample operating time N/N* (N is the current number of loading cycles, N* is the number of cycles corresponding to complete sample failure).

Fig. 4.
figure 4

Microstructures after fatigue loading of samples cut from the overheating (a) and normalizing (b) sites of heat affected zone during St3 welding.

Full size image

In the process of cyclic loading, a large number of stable slip bands in individual ferrite grains in the form of thin lines is observed already at the initial stage (see Fig. 4). However, slip bands at the normalizing site of the heat affected zone are visible only in a small number of ferrite grains, whereas during loading, slip bands at the overheating site are observed in all grains. In the process of further fatigue loading, there is also a considerable increase in the concentration of slip bands in the grains and the formation of a large number of dark areas in the microstructure; this is associated with constrained rotation and fragmentation of grains during material failure and leads to a change in the conditions of light reflection (angle and reflection coefficient) from the material surface.

The microcrack nucleation mechanism associated with slip bands is given in [19]. Studies show that the boundary between the sample surface and the extrusion area serves as a stress raiser that can lead to the formation of a fatigue crack.

The occurrence of a main crack in the normalizing area of the heat affected zone is observed with an operating time of the order of N/N* = 0.6–0.7. In the studied area of overheating of the heat affected zone, the main crack is formed with an operating time of the order of 0.85–0.95 and grows at a high rate. In this case, the formation of the main crack is observed in the domains with the highest concentration of slip bands, so in the overheating zone its nucleation and growth occurs mainly at the boundaries of ferrite grains while in the normalizing zone, the main crack passes through both ferrite grains and intergranular space.

On the basis of digital image processing, the concentration of slip bands and defects in material structure (n) was determined at various stages of loading (Fig. 5). As can be seen from the above dependences, the concentration n differs (up to 2 times) at the normalizing and overheating sites of the heat affected zone. With an increase in the stress amplitude, a significant increase in the concentration n is observed at all stages of the test.

Fig. 5.
figure 5

Dependence of the specific number of defects and slip bands (n) in a microstructure image on the sample operating time at the overheating and normalizing sites of heat affected zone with σmax equal to 250 and 270 MPa.

Full size image

The fraction (Srel) of microstructure defects and slip bands formed during fatigue tests was also determined. The dependence of Srel on the relative number of loading cycles is shown in Fig. 6.

Fig. 6.
figure 6

Dependence of the fraction (Srel) of defects and slip bands formed during cyclic loading on the sample operating time at the overheating and normalizing sites of heat affected zone with stress amplitudes in the cycle σmax equal to 250 and 270 MPa.

Full size image

Analysis of the obtained dependences (see Figs. 5 and 6) shows that the accumulation of structural damage occurs with different intensity at different sites of the heat affected zone. Thus, in the process of fatigue tests, a monotonous increase in the total number and relative area of slip bands and microdefects in the structure of St3 steel is observed up to the formation of the main crack. After the occurrence of the main crack, the index Srel remains practically unchanged, and the specific number of defects and slip bands in the structure decreases, primarily due to the fusion of individual defects and slip bands during the growth of a fatigue crack.

Based on the preliminary processing of images of structures in the process of cyclic loading, the fractal dimension (Df) of the image of microstructures at different stages of testing for different stress amplitudes was determined. The initial values of the fractal dimension of the microstructure image for the overheating and normalizing sites of the heat affected zone were 1.895 ± 0.004 and 1.867 ± 0.003, respectively. This difference is explained, first of all, by different grain sizes and proportions of boundaries; this substantially affects the fractal dimension index. In this regard, it makes sense to consider the fractal dimension increment ΔDf versus the sample operating time. The obtained dependences of the fractal dimension increment ΔDf  on the sample operating time for the overheating and normalizing sites of the heat affected zone are shown in Fig. 7.

Fig. 7.
figure 7

Dependence of the increment of fractal dimension of microstructure images on the sample operating time at the overheating (1) and normalizing (2) sites of heat affected zone with stress amplitudes in the cycle σmax equal to 250 (A) and 270 MPa (B).

Full size image

The analysis of the dependence in Fig. 7 shows that a monotonous decrease in the fractal dimension of the sample is observed in the process of elastic-plastic cyclic deformation. This is consistent with the results of microstructural studies (see Fig. 4). However, a change in the nature of the dependence of the fractal dimension is observed in the main crack zone on the presented dependences; this correlates and agrees with the results of determining quantitative microstructure indicators (see Figs. 5, 6). With an increase in the applied stress amplitude, a more intense change is observed in the fractal dimension of the image of the microstructure of the sample working area.

Thus, the given quantitative characteristics of alloy microstructure allow one to assess the operating time and accumulated structural damage of the sample material at various sites of the welding process and reflect the physical processes occurring in the material at various stages of elastic-plastic cyclic deformation. When calculating quantitative characteristics and in the subsequent prediction of microstructure damage, it is necessary to take into account the material grain size, because it has a considerable impact on the processes of deformation and destruction of the structural material under fatigue.

Figure 8a shows the dependence of the acoustic parameter Ds. The analysis of the obtained dependence makes it possible to conclude that under fatigue loading of samples cut from the overheating and normalizing sites of St3 steel, there are two stages of decrease in the value of Ds. For all the studied sections of the heat affected zone, there is a change in the nature of the dependence in the operating time range ~N/N* = 0.6. Before the specified operating time, the parameter Ds of the sample from the normalizing site remains virtually unchanged, a fact that is in good agreement with microstructural studies, after which the parameter Ds begins to decrease due to the intensification of the occurrence and fusion of structural defects. This behavior may be associated with the beginning of the occurrence and development of microcrack systems and with a decrease in the velocities of elastic waves and hence a decrease in the values of all elastic properties of material. On the sample from the overheating site, the process of structural degradation occurs more intensively (see Fig. 4a). Accumulation and increase in the fraction of structural defects (see Fig. 6) begins after several loading cycles and gradually increases as the operating time increases; this affects the acoustic parameter Ds.

Fig. 8.
figure 8

Dependence of acoustic parameter Ds (a) and coercive force Hc (b) on the sample operating time.

Full size image

A similar result is obtained when measuring the magnetic characteristic Hc (Fig. 8b), this also confirms the stage-by-stage fatigue failure of St3 steel sections. The increase in the values of the coercive force Hc is characterized by difficulty in the process of magnetization and remagnetization. The reasons for the increase in Hc are an increase in the degree of distortion of the crystal lattice during deformation under fatigue loading and the phenomenon of cold-work hardening, accompanied by an increase in the density of defects with higher values of the critical fields of interaction of domain boundaries with defects in the alloy structure [20].

In the course of the study, an analysis of the microhardness of the overheating and normalizing sites of St3 steel after various operating times was carried out. The results of the research are illustrated by Fig. 9.

Fig. 9.
figure 9

Dependence of the microhardness of sections of St3 steel on the sample operating time.

Full size image

It is shown that the change in the material hardness from the overheating site differs considerably from the behavior of the hardness in the sample from the normalizing site, characterized by a finer grain. The increase in the microhardness of the sample from the normalizing site with increase in operating time is monotone, and it is only after the operating time ~N/N* = 0.8 (it corresponds to the moment of formation of main cracks) that it has a considerable increase associated with the intensification of deformation processes (hardening). The dependence of the microhardness on the operating time of a coarse grained sample (45 μm, overheating site) is of a different nature. Until the operating time ~N/N* = 0.2, one can observe an intensive increase in microhardness due to a large degree of deformation at the initial stages of fatigue loading (substantial cold-work hardening and an increase in dislocation density) in favorably located (from the point of view of deformation) grains. The presence of a large grain and a small fraction of large-angle boundaries contribute to a decrease in strength characteristics (στ, σt) in accordance with the Hall–Petch law (σy = σ0 + Kd–1/2, where d is the grain size). A further gradual decrease in microhardness is associated with the appearance and development of systems of microcracks and structural looseness (accumulation of discontinuities). After the operating time ~N/N* = 0.7, a rapid decrease is observed in the values of microhardness that is associated with the unification of various systems of structural defects preceding the failure.

CONCLUSIONS

1. The process of cyclic loading of the normalizing and overheating sites of St3 steel at a stress level exceeding the yield strength is characterized by the formation of a large number of structural defects (deformation bands, discontinuities, etc.), while the processes of structural degradation of the overheating section proceed more intensively. This is associated with a larger grain size (four times larger than at the normalizing site).

2. Determination of numerical parameters (fractal dimension, number of defects, fraction of structural defects) of microstructures of the heat affected zone in St3 steel at various operating time levels has shown that these structure parameters are informative and can be used to monitor the level of structural damage during cyclic loading of structures.

3. Measurements of the structure-sensitive acoustic parameter and coercive force have shown that the formation of slip bands and an increase in the defectiveness of the structure during fatigue structural degradation can be quickly evaluated using the indicated parameters.

4. The results of the research carried out can be applied in the problems of diagnosing premature failure and monitoring the most loaded zones of St3 steel structures in order to determine their residual resource.