Abstract
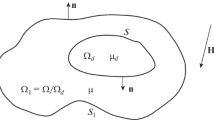
An equation for determining the magnetic field of a plate inside which there is a cavity of finite dimensions with a smooth boundary has been obtained on the basis of the integro-differential equation of magnetostatics. A particular problem has been solved for a spherical cavity and an external uniform magnetizing field directed parallel to the plate surface.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Dyakin, V.V. and Umergalina, O.V., On Calculation of the Field of a Flaw in a 3D Half-Space, Defektoskopiya, 2003, no. 4, pp. 52–66 [Rus. J. Nondestr. Test. (Engl. Transl.), 2003, vol. 39, no. 4, pp. 297–309].
Dyakin, V.V., Umergalina, O.V., and Raevskii, V.Ya., Field of a Finite Flaw in a 3D Space, Defektoskopiya, 2005, no. 8, pp. 28–42 [Rus. J. Nondestr. Test. (Engl. Transl.), 2005, vol. 41, no. 8, pp. 502–513 ].
Dyakin, V.V., Raevskii, V.Ya., and Umergalina, O.V., Magnetostatic Problem for a Half-Space with a Spherical Flaw in a Nonuniform External Field, Defektoskopiya, 2007, no. 1, pp. 3–15 [Rus. J. Nondestr. Test. (Engl. Transl.), 2007, vol. 43, no. 1, pp. 1–11].
Dyakin, V.V., Raevskii, V.Ya., and Umergalina, O.V., Magnetostatic Problem for a Half-Space with a Spherical Flaw in the Field of a Coil, Defektoskopiya, 2008, no. 2, pp. 36–49 [Rus. J. Nondestr. Test. (Engl. Transl.), 2008, vol. 44, no. 2, pp. 102–112].
Mikhlin, S.G., Lineinye uravneniya v chastnykh proizvodnykh (Linear Equations in Partial Derivatives), Moscow: Vysshaya shkola, 1977.
Gradshtein, I.S. and Ryzhik, I.M., Tablitsy integralov, summ, ryadov i proizvedenii (Tables of Integrals, Sums, Series, and Products), Moscow: GIFML, 1962.
Varshalovich, D.A., Moskalev, A.N., and Khersonskii, V.K., Kvantovaya teoriya uglovogo momenta (Quantum Theory of Angular Momentum), Leningrad: Nauka, 1975.
Sandovskii, V.A., Dyakin, V.V., and Umergalina, O.V., Field of a Flaw in the Form of an Elliptical Cylinder in a Plate Placed in a Uniform Magnetic Field, Defektoskopiya, 1999, no. 11, pp. 46–56.
Shcherbinin, V.E. and Pashagin, A.I., Influence of the Boundaries of an Object on the Value of the Flaw Field, Defektoskopiya, 1976, no. 2, pp. 85–89.
Shcherbinin, V.E. and Shur, M.Ya., Consideration of the Influence of the Boundary of an Article on the Field of a Cylindrical Flaw, Defektoskopiya, 1976, no. 6, pp. 30–36.
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © V.V. Dyakin, V.Ya. Rayevskiy, O.V. Kudrjashova, 2009, published in Defektoskopiya, 2009, Vol. 45, No. 3, pp. 67–79.
Rights and permissions
About this article
Cite this article
Dyakin, V.V., Rayevskiy, V.Y. & Kudrjashova, O.V. The field of a finite defect in a plate. Russ J Nondestruct Test 45, 199–209 (2009). https://doi.org/10.1134/S1061830909030073
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1061830909030073