Skip to main content
SpringerLink
Log in

Stray Field of Plate with a Surface Defect in a Homogeneous External Field

  • Electromagnetic Methods
  • Published:
Russian Journal of Nondestructive Testing Aims and scope Submit manuscript

Abstract

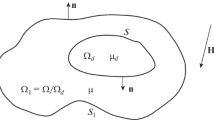
The two-dimensional problem of magnetostatics has been solved by calculating the resultant field of the plate with a surface defect, placed in a homogeneous external field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zatsepin, N.N. and Shcherbinin, V.E., To the calculation of magnetostatic field of surface defects, Defektoskopiya, 1966, no. 5, pp. 50–59.

    Google Scholar 

  2. Krotov, L.N., Shleenkov, A.S., and Shcherbinin, V.E., Computer simulation of magnetic fields of defects. Twodimensional problem, Defektoskopiya, 1995, no. 9, pp. 27–32.

    Google Scholar 

  3. Krotov, L.N., Simulation of the inverse geometric problem of magnetostatics in magnetic testing, Extended Abstract of Doctoral (Phys.-Math.) Dissertation, Perm, 2004.

    Google Scholar 

  4. Dyakin, V.V., Matematicheskiye osnovy klassicheskoy magnitostatiki (Mathematical Foundations of Classical Magnetostatics), Yekaterinburg, 2016.

    Google Scholar 

  5. Mikhlin, S.G., Lineinye uravneniya v chastnykh prozivodnykh (Linear Partial Differential Equations), Moscow: Vyssh. Shkola, 1977.

    Google Scholar 

  6. Khizhnyak, N.A., Integral’nye uravneniya makroskopicheskoi elektrodinamiki (Integral Equations of Macroscopic Electrodynamics), Kiev: Naukova Dumka, 1986.

    Google Scholar 

  7. Tamm, I.E., Osnovy teorii elektrichestva (Fundamentals of Theory of Electricity), Moscow: Fizmatlit, Nauka, 1989.

    Google Scholar 

  8. Korn, G. and Korn, T., Spravochnik po matematike dlya nauchnykh rabotnikov i inzhenerov (Handbook of Mathematics for Scientists and Engineers), Moscow: Fizmatlit, Nauka, 1970.

    Google Scholar 

  9. Il’in, V.A., Sadovnichii, V.A., and Sendov, B.Kh., Matematicheskii analiz. Ch. II (Calculus. Part II), Moscow: Moscow State Univ., 2007.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mikheev Institute of Metal Physics, Ural Branch, Russian Academy of Sciences, Yekaterinburg, 620108, Russia

    V. V. Dyakin, O. V. Kudryashova & V. Ya. Raevskii

Authors
  1. V. V. Dyakin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. V. Kudryashova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. Ya. Raevskii
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. Ya. Raevskii.

Additional information

Original Russian Text © V.V. Dyakin, O.V. Kudryashova, V.Ya. Raevskii, 2018, published in Defektoskopiya, 2018, No. 12, pp. 23–30.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dyakin, V.V., Kudryashova, O.V. & Raevskii, V.Y. Stray Field of Plate with a Surface Defect in a Homogeneous External Field. Russ J Nondestruct Test 54, 840–848 (2018). https://doi.org/10.1134/S1061830918120033

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1061830918120033

Keywords

Search

Navigation