As photo and video recording technology developed, new components were discovered in the pattern of coalescence of a drop with a liquid, including the cavity, crown, jets, splash [1], and capillary and acoustic waves [2]. Multifrequency lightning in the optical and X-ray band [3] showed the initial multilayered structure of the thin ejecta sheet [4] coalescing into the crown. From the vertices of spikes at the teeth of the eject sheet, groups of small droplets emerge cyclically [5]. The drop contact is accompanied by generation of a high-frequency sound packets [2, 6]. To refine the mechanisms of sound generation, the mechanisms of formation of oscillating single bubbles [7] and groups of bubbles forming ring structures [8] are investigated.

The drop matter is captured by the ring vortex encircling the cavity and partly remains on the liquid surface [9, 10]. The falling drop is spread uniformly or generates banded structures of fast conversion of the available potential surface energy [10]. The experiments complement the analytical [11] and numerical [12] studies of drop flows based on the system of Navier–Stokes equations.

Investigation of the cavity dynamics is related to development of the methods for remote sensing of the Earth and is caused by the dependence of the scattered signal on the size of inhomogeneities of the water surface [13]. In the present experiments, the dynamics of the delayed process of cavity formation in the intrusive mode of coalescence was studied first.

The drops fell into a basin with dimensions of 30 × 30 × 5 cm or 10 × 10 × 7 cm filled with tap water [14]. The flow pattern was illuminated by the ReyLab Xenos RH-1000 studio lighting strands or by Optronis MultiLED LED sources and registered by an Optronis CR 300x2 videocamera or by a Canon EOS 350D photo camera, which were triggered by the photodetector recording the flight of the drop (the technique was described in [6, 10]).

The process parameters include the air density ρa and the water density ρd (in the following, \({{\rho }_{{a,d}}}\)), the kinematic \({{\nu }_{{a,d}}}\) and dynamic \({{\mu }_{{a,d}}}\) viscosities of media, the total \(\sigma _{d}^{a}\) and the normalized coefficient of the surface tension \(\gamma = \frac{{\sigma _{d}^{a}}}{{{{\rho }_{d}}}}\) cm3/s2, the gravity acceleration g, the diameter D, the surface area Sd, the volume V, the mass M, the velocity U at the instance of contact, the duration of the drop coalescence \({{\tau }_{D}} = \frac{D}{U}\) s, the available potential surface energy (APSE) \({{E}_{\sigma }} = \sigma {{S}_{d}}\) concentrated in the spherical layer with a thickness near the size of the molecular cluster \({{\delta }_{\sigma }}\sim {{10}^{{ - 6}}}\) cm, and the kinetic energy \({{E}_{d}} = \frac{{M{{U}^{2}}}}{2}\). The characteristic time for conversion of the surface energy to other forms of energy depends on the drop velocity which determines the duration of coalescence of subsurface layers \({{\tau }_{\sigma }}\sim \frac{{{{\delta }_{\sigma }}}}{U} \ll {{\tau }_{D}}\).

Drops of water or of an alizarin ink water solution with the diameter \(D = 0.42\) cm fell freely from a height of \(0.6 < H < 200.0\) cm. The velocity at the contact 0.34 \( < U < \) 4.3 m/s was determined by video recordings. The surface energy was \({{E}_{\sigma }} = 4\) μJ, and the kinetic energy ranged in the interval 2.24 \( < {{E}_{k}} < \) 360 μJ. The parameters of the experiments were as follows: the Reynolds number is \(1450 < \operatorname{Re} = \frac{{UD}}{\nu } < 18\,000\), the Froude number is \({\text{2}}{\text{.8 < Fr}} = \frac{{{{U}^{2}}}}{{gD}} < 450\), the Bond number is Bo = \(\frac{{g{{D}^{2}}}}{\gamma }\) = 2.39, the Ohnesorge number is \({\text{Oh}} = \frac{\nu }{{\sqrt {\gamma D} }}\) = 0.0018, and the Weber number is 6.7 \( < We = \frac{{{{U}^{2}}D}}{\gamma }\) < 1100.

The dynamics and the geometry of the flow upon coalescence of a drop with the target liquid are dependent on the ratio of the APSE \({{E}_{\sigma }}\) to the kinetic energy \({{E}_{k}}\). At small velocities of incidence (\({{E}_{k}} < {{E}_{\sigma }}\)), when the inflowing drop forms an intrusion, i.e., the continuous volume of colored liquid, the generation of the cavity begins with a delay. At high velocities of drop incidence, the cavity and the crown uniformly or discretely colored by the drop matter are immediately formed.

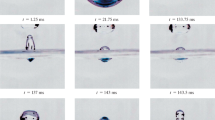
Samples of video recordings of the flow pattern in the intrusive mode are given in Fig. 1 (here, in the vicinity of the liquid surface, there is a blind zone with a height of 1.5 mm caused by capillary rise near the wall). Over a short trajectory, the drop does not contract to the sphere and consists of a central cylindrical part and two head parts, the lower spherical one and the upper planar one. The velocity of the drop with the diameter \(D = \) 0.42 cm is equal to \(U = 0.34\) m/s, the APSE \({{E}_{\sigma }} = 4\) μJ is larger than the kinetic energy \({{E}_{k}} = \) 2.24 μJ, and the dimensionless numbers are as follows: Re = 1450, Fr = 2.8, Bo = 2.39, Oh = 0.0018, and We = 6.7. The incoming drop oscillates and is covered by short capillary waves with the lengths \({{\lambda }_{c}} = \) 0.46 and 0.54 mm (t = 0.0 ms, Fig. 1).

Fig. 1.
figure 1

Formation of intrusion, cavity, and small vortices upon slow coalescence between an ink drop (with a concentration of 1 : 1000) and water; the width of the frame is 1 cm.

Full size image

Under submergence of the head part, the circle contact line of coalescing liquids at which the APSE is released and thin subsurface flows, i.e., the ligaments, are formed moves outward [10]. The ligaments distribute the energy and momentum of the coalesced part of the drop over the surface of the incoming liquid, which generates an intrusion with a convex bottom and upper boundaries at the center of which the remainder of the drop taking a conical form is situated (\(t = \) 6.4 ms, Fig. 1). Ring capillary waves propagate from the contact line in both directions.

Upon submergence of the bottom part of the drop, the coalescence line contracts towards the center of the flow, the contact area decreases, and, simultaneously with annihilation of the drop surface, the new free surface is formed. Now, ligaments transfer a part of the converted energy and momentum of the drop back into the contact patch. Here, the rate of increase in the cavity width decreases sharply from \({{{v}}_{r}} = 2.13\) m/s at \(t = \) 6.0 ms to \({{{v}}_{r}} = 0.44\) m/s at \(t = \) 6.2 ms.

A part of the intrusion detaches from the free surface and curls in a ring vortex with the ring diameter \({{d}_{i}} = \) 1.93 mm and the envelope diameter \({{D}_{i}} = \) 6.63 mm; part of it remains in the subsurface layer (t = 11.5 ms, Fig. 1). The surface of the liquid bends smoothly, and a cavity with a conical foundation and a cylindrical central part (not seen in this projection) is generated at its center. The cavity dimensions increase rapidly, and at t = 19.1 ms its depth is equal to \({{h}_{c}} = \) 3.1 mm. The diameter of the central cylindrical part is \({{d}_{c}} = \) 3.24 mm, and the diameter of the foundation at the free surface is \({{d}_{s}} = \) 6.57 mm.

The increasing cavity pushes the central part of the vortex the toroidal part of which is behind by a height \({{h}_{i}} = \) 1.73 mm from the bottom edge of the intrusion from the apex of which a small vortex ring with \({{d}_{1}} = \) 0.58 mm and a new toroidal small vortex with diameter \({{d}_{{v}}} = \) 0.8 mm at its stem \({{d}_{b}} = \) 0.64 mm and height \({{h}_{b}} = \) 0.1 mm are ejected.

Under the action of the buoyancy forces, the cavity collapses (t = 24.7 ms, Fig. 1) and detaches from the uniformly submerging intrusion recovering its toroidal shape. The sizes of small vortices under the intrusion grow slowly.

After collapse of the cavity, the toroidal vortex with a head with diameter \({{D}_{i}} = \) 5.7 mm remains in the liquid; the colored veil is delaminated from this vortex; the vortex is connected by a stem with the diameter d  = 2 mm to the subsurface lens with diameter \({{D}_{s}} = \) 9.4 mm at t = 34 ms, which is colored by the drop liquid. Then, the subsurface part of the intrusion continues to expand and thin and the decelerating vortex submerges into the liquid.

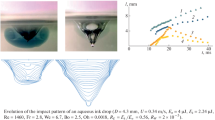
The evolution of the flow pattern at the free surface (observation at an angle of 65° to the horizon) upon coalescence of the drop of the diluted ink water solution (with a concentration of 1 : 2500) is shown in Fig. 2 (\(D = \) 0.42 cm, \(U = 0.34\) m/s, \({{E}_{\sigma }} = 4\) μJ, \({{E}_{k}} = \) 2.24 μJ, Re = 1450, Fr = 2.8, Bo = 2.39, Oh = 0.0018, and We = 6.7). The shadows and caustics draw the depression of the ring capillary wave near the drop apex.

Fig. 2.
figure 2

A drop of the alizarin ink water solution (with a concentration of 1 : 2500) submerges into pure water; the length of the mark is 1 cm.

Full size image

In the region of drop coalescence, at a distance of \(\Delta r\) = 1.17 mm from the ring capillary wave, there is the edge of the intrusion with a diameter of \({{d}_{i}} = \) 4.6 mm with an inhomogeneous distribution of matter (\(t = \) 0.85 ms, Fig. 2). In the upper part of the figure, near the nozzle section, we see the falling secondary satellite, the remainder of the bridge, with diameter \({{d}_{s}} = \) 0.88 mm.

The number of capillary waves on the drop remainder and in the target liquid with lengths \({{\lambda }_{c}} = \) 3.3, 3.4, 3.7, 3.9, and 6.4 mm increases with time (t = 2.8 ms, Fig. 2). The spreading liquid is situated in a circle with diameter \({{d}_{i}} = \) 5.0 mm inside the ring of waves. Here, the free surface is smooth and convex and there is no cavity. The lower part of the drop expands following the flow in the intrusion.

A cavity with diameter \({{d}_{c}} = \) 5.47 mm appears when part of the drop has submerged and the diameter of the remainder is equal to \(d = \) 2.3 mm (t = 6.2 ms, Fig. 2). The cavity walls are visualized by dark circles and a caustic in the direction of 13 hours. The colored liquid around the cavity lies in a ring with diameter \({{d}_{i}} = \) 6.25 mm and width \(\Delta {{r}_{i}} = \) 0.98 mm, at the outer contour of which we see radial looped structures with the step \(\Delta {{l}_{\varphi }} = \) 0.4 ± 0.1 mm and thickness \(\Delta {{r}_{p}} \sim \) 1 mm prominent outside the boundary of the colored region by \(\Delta {{r}_{e}} = \) 0.2 mm.

In the center of the deepened cavity, there remains a bulge (\({{d}_{d}} = \) 1.2 mm, t = 8.7 ms, Fig. 2). The cavity remainder and the group of ring waves with lengths \({{\lambda }_{c}} = \) 4.6, 6.7, 7.34, 7.8, 8.7, and 12 mm are divided by a smooth ring with width \(\Delta {{r}_{r}} = \) 3.26 mm. The diameter of the region of colored liquid here decreases upon cavity collapse as in Fig. 1, t = 34 ms.

At large velocities of falling, at the initial stage, the drop matter appears to be concentrated on the cavity walls (Fig. 3, \(D = \) 0.42 cm, \(U = \) 4.3 m/s, Re = 18 000, \({\text{Fr}} = \) 450, \({\text{Bo}} = \) 2.39, \({\text{Oh}} = \) 0.0018, \(We = \) 1100, \({{E}_{k}} = \) 358.6 μJ, \({{E}_{\sigma }} = 4\) μJ, and t = 0.5 ms). The sizes of the cavity, crown, and ejecta sheet with sharp teeth increase with time (t = 2 ms, Fig. 3). The vertices of the teeth are adjacent to the spikes from the sharp tips of which sputter emerges. The drop matter forms linear structures on the surface of the cavity and crown [10].

Fig. 3.
figure 3

Coalescence of a drop of alizarin ink water solution (with a concentration of 1 : 200) with water; the length of the mark is 1 cm.

Full size image

The drop matter at the cavity walls gradually begins to intrude into the surrounding medium somewhat faster than the cavity wall moves, and its contour becomes irregular with prominent segments (t = 11 ms, Fig. 3). The ejecta sheet over the crown begins to contract, but the tips of spikes are still oriented outward. The thickness of the crown and cupola and the sizes of droplets increase, and the irregularity of the coloring of the cavity bottom becomes more pronounced (t = 26 ms, Fig. 3). The length of capillary waves at the surface of the cupola decreases from 0.8 to 0.75 mm towards the apex of the cupola.

It follows from comparison of Figs. 1 and 3 and the measurement data in Fig. 4 that the flow pattern depends on the ratio between the APSE \({{E}_{\sigma }}\) and the kinetic energy of the drop \({{E}_{k}}\). For a slowly falling drop, when \({{E}_{\sigma }} > {{E}_{k}}\), in the initial segment until label II (а at \(t < \) 5.32 ms), when the surfaces of both liquids are simultaneously annihilated, the drop rapidly spreads and its width is approximated by the function \({{w}_{i}} = 0.2{{t}^{2}}\) + 5.3 (curve 1, segment а; the interval of the hidden position of the cavity is dashed).

Fig. 4.
figure 4

Flow geometry: curves 1 and 2 are for the diameter and length of intrusion submergence, curves 3 and 4 are for the diameter of the cylindrical part and the depth of the cavity in the intrusive mode, and curves 5 and 6 are for the diameter and depth of the cavity in the mode of drop spreading.

Full size image

The rate of increase in the intrusion width decreases after submergence of the front part of the drop from 2.13 to 0.44 m/s at t = 6.2 ms (label III). Formation of a new surface of the target liquid causes reduction in the growth of the intrusion width (curve 1, segment b, \({{w}_{i}} = 0.00084{{t}^{3}} - 0.05{{t}^{2}} + 0.9t + 1.7\)), which reaches its maximum at t = 12 ms (label IV, end of the drop coalescence). The intrusion depth along the entire interval of observation \(2 < t < 31\) ms (curve 2, Fig. 4) increases linearly as \({{h}_{i}} = 0.255t\).

The width of the cavity formed wc = \(0.008{{t}^{3}}\) – 0.468t2 + 9t – 53.5 (segment с of curve 3) and its depth \({{h}_{c}} = 0.0036{{t}^{3}} - 0.23{{t}^{2}} + 4.8t - 29.7\) (segment e of curve 4) increase practically synchronously. The cavity depth reaches its maximum at t = 17 ms (label V). At t = 23 ms (label VI), the cavity begins to expand rapidly (\({{w}_{c}} = 0.66t\) at segment d), the depth begins to decrease slowly (\({{h}_{i}} = \frac{{23}}{t}\) at segment f), and the intrusion height begins to exceed its width.

Upon coalescence of a rapidly falling drop (\({{\tau }_{D}} = \) 0.98 ms), the phase of growth in the horizontal dimension of the cavity (curve 5) is described by the power function \({{w}_{c}} = 7.4{{t}^{{0.3}}}\) until t = 49 ms (label IX). After that, the cavity width begins to decrease slowly. At the initial stage, the cavity depth increases monotonically \({{h}_{c}} = 2.8{{t}^{{0.5}}}\) (segment n of curve 6) until t = 11.4 ms (label VII), reaches its maximum at t = 24 ms (label VIII), and then decreases monotonically as hc = \(0.00013{{t}^{3}}\) – 0.021t2 + 0.81t + 2 (segment m of curve 6).