Turbulent Flow past a Flat Plate at Zero Incidence

Abstract

The dissipation theorem is applied to fully developed turbulent flow past a flat plate. Most of the velocity profile occurs in a thin layer near the surface, but a layer of turbulence (represented by the eddy viscosity) extends substantially farther into the fluid.

APPENDIX A

DECAY OF DISSIPATION

We need to ascertain exactly what form was used for the dimensional Decay in pipe flow because we need to know what to use in other geometries and also to tell others what we are doing.

The central idea behind the dissipation theorem is that turbulence should be described by several mathematical relationships among local statistical quantities, particularly the total stress, the eddy viscosity, and the volumetric dissipation. Hence, the dissipation theorem describes how the volumetric dissipation ${{\mathcal{D}}_{V}}$ changes with time, convection, diffusion, and decay:

$$\begin{gathered} \frac{{\partial {{\mathcal{D}}_{V}}}}{{\partial t}} + {\mathbf{\bar {v}}} \cdot \nabla {{\mathcal{D}}_{V}} \\ = \nabla \cdot \left( {\left( {\nu + {{\nu }^{{(t)}}}} \right)\nabla {{\mathcal{D}}_{V}}} \right){-}\text{Decay}, \\ \end{gathered} $$

(A1)

where ${\mathbf{\bar {v}}}$ is the average velocity, diffusion is described by the kinematic viscosity ν and the eddy kinematic viscosity ν^(t), and Decay is the dimensional decay. This equation attempts to show the vector nature of the quantities. However, ν^(t) is really a tensor which is approximated as a scalar in certain systems of turbulent shear.

For steady turbulent flow in a cylindrical pipe, this equation becomes

$$0 = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r(\nu + {{\nu }^{{(t)}}})\frac{{\partial {{\mathcal{D}}_{V}}}}{{\partial r}}} \right]{-}\text{Decay}.$$

(A2)

Diffusion in the longitudinal direction is neglected, and only one component of the tensor eddy viscosity is needed.

Dimensionless variables are chosen as follows:

$$\xi = \frac{r}{R},{\text{ }}G = \frac{{\nu + {{\nu }^{{(t)}}}}}{\nu },{\text{ and }}{{D}_{p}} = \frac{{\mu {{\mathcal{D}}_{V}}}}{{\tau _{0}^{2}}},$$

(A3)

the last being chosen so that D_p = 1 on the wall of the pipe. (The subscript p on D_p is to distinguish D_p from D used with flow past a flat plate.) R is the radius of the pipe, and τ₀ is the magnitude of the stress at the wall of the pipe. Substitution gives

$$\frac{1}{\xi }\frac{\partial }{{\partial \xi }}\left[ {\xi G\frac{{\partial D}}{{\partial \xi }}} \right] = \frac{{\mu {{R}^{2}}}}{{\tau _{0}^{2}\nu }}{\text{Decay}} = {\text{deca}}{{{\text{y}}}_{p}}.$$

(A4)

One can say that τ₀/R = τ/r for this geometry, so that τ is a local variable. For turbulent pipe flow, the dimensional Decay and the dimensionless decay_p are related as shown in equation (A4).

By reverse engineering of Nikuradse’s data, we find that decay depends mainly on R⁺D_p/ξ, with both a quadratic and a linear term. We write this as

$${\text{deca}}{{{\text{y}}}_{p}} = \Lambda {{\left( {\frac{{{{D}_{p}}{{R}^{ + }}}}{\xi }} \right)}^{2}} + \Lambda \varepsilon \frac{{{{D}_{p}}{{R}^{ + }}}}{\xi }{\text{ }}.$$

(A5)

(There are also a term D_pR⁺ and a 4, which can perhaps be ignored.) Thus, Decay becomes

$$\begin{gathered} {\text{Decay}} = \frac{{\tau _{0}^{2}}}{{\rho {{R}^{2}}}}\Lambda {{\left( {\frac{{\mu {{\mathcal{D}}_{V}}}}{{\tau _{0}^{2}}}\frac{R}{\nu }\sqrt {\frac{{{{\tau }_{{\text{0}}}}}}{\rho }} {\text{ }}\frac{{{{\tau }_{{\text{0}}}}}}{\tau }} \right)}^{2}} \\ + \,\,\frac{{\tau _{0}^{2}}}{{\rho {{R}^{2}}}}\Lambda \varepsilon \frac{{\mu {{\mathcal{D}}_{V}}}}{{\tau _{0}^{2}}}\frac{R}{\nu }\sqrt {\frac{{{{\tau }_{{\text{0}}}}}}{\rho }} {\text{ }}\frac{{{{\tau }_{{\text{0}}}}}}{\tau } \\ \end{gathered} $$

$$ = \Lambda {{\tau }_{{\text{0}}}}{{\left( {\frac{{{{\mathcal{D}}_{V}}}}{\tau }} \right)}^{2}} + \Lambda \varepsilon \frac{{{{\mathcal{D}}_{V}}}}{\tau }\frac{{{{\tau }_{{\text{0}}}}}}{R}\sqrt {\frac{{{{\tau }_{{\text{0}}}}}}{\rho }} {\text{ }}{\text{.}}$$

(A6)

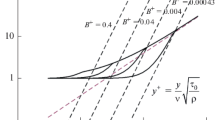
Preferred values are Λ = 0.17 and ε = 0.33. (Earlier ε was used with a different meaning, including a dependence on R⁺.) In addition, the viscous sublayer is grafted in with a value of B⁺ = 0.0005. [If the wall stress τ₀ can be taken to be known, the problem becomes more like the problems with the pipe and the rotating cylinders.]

The scaling for the flat plate is different from that for the pipe. R and τ₀ are nonlocal variables. For the flat plate, equation 1 and

$${\text{Decay }} = {\text{ }}\rho \frac{{{\text{v}}_{\infty }^{{\text{6}}}}}{{{{\nu }^{{\text{2}}}}}}{\text{ decay}} = \rho \frac{{{\text{v}}_{\infty }^{{\text{6}}}}}{{{{\nu }^{{\text{2}}}}}}\frac{{\Lambda D_{1}^{2}}}{{{{{(\xi {{R}^{ + }})}}^{2}}}},$$

(A7)

apply. Thus

$${\text{decay}} = \frac{{\Lambda {{\tau }_{{\text{0}}}}}}{{\rho v_{\infty }^{{\text{2}}}}}{{\left( {\frac{{{{D}_{1}}}}{{{{T}_{1}}}}} \right)}^{2}} + \frac{{\Lambda \varepsilon {{\tau }_{{\text{0}}}}}}{{\rho v_{\infty }^{{\text{2}}}}}\frac{{{{D}_{1}}}}{{{{T}_{1}}}}\frac{{\nu {{v}_{*}}}}{{Rv_{\infty }^{{\text{2}}}}}{\text{ }}{\text{,}}$$

(A8)

where ${{v}_{*}}$ = (τ₀/ρ)^0.5.

The dissipation-theorem equation takes the form

$${{v}_{x}}\frac{{\partial {{\mathcal{D}}_{V}}}}{{\partial x}} + {{v}_{y}}\frac{{\partial {{\mathcal{D}}_{V}}}}{{\partial y}} = \nu \frac{\partial }{{\partial y}}\left( {G\frac{{\partial {{\mathcal{D}}_{V}}}}{{\partial y}}} \right) - {\text{Decay}}{\text{,}}$$

(A9)

or

$${{V}_{x}}\frac{{\partial {{D}_{1}}}}{{\partial \chi }} + {{V}_{y}}\frac{{\partial {{D}_{1}}}}{{\partial Y}} = \frac{\partial }{{\partial Y}}\left( {G\frac{{\partial {{D}_{1}}}}{{\partial Y}}} \right) - \frac{{{{\nu }^{2}}}}{{\rho {\text{v}}_{\infty }^{{\text{6}}}}}{\text{Decay}}{\text{.}}$$

(A10)

This becomes

$$\begin{gathered} {{V}_{x}}\frac{{\partial {{D}_{1}}}}{{\partial \chi }} + {{V}_{y}}\frac{{\partial {{D}_{1}}}}{{\partial Y}} = \frac{\partial }{{\partial Y}}\left( {G\frac{{\partial {{D}_{1}}}}{{\partial Y}}} \right) - \frac{{\Lambda {{\tau }_{{\text{0}}}}}}{{\rho v_{\infty }^{{\text{2}}}}}{{\left( {\frac{{{{D}_{1}}}}{{{{T}_{1}}}}} \right)}^{2}} \\ - \,\,\frac{{\Lambda \varepsilon {{\tau }_{{\text{0}}}}}}{{\rho v_{\infty }^{{\text{2}}}}}\frac{{{{D}_{1}}}}{{{{T}_{1}}}}\frac{{\nu {{v}_{*}}}}{{Rv_{\infty }^{{\text{2}}}}}{\text{ }}{\text{.}} \\ \end{gathered} $$

(A11)

After the similarity transformation, the dissipation theorem equation becomes (see equation (6))

$$\begin{gathered} f'\chi \frac{{\partial {{D}_{1}}}}{{\partial \chi }} - \frac{{\partial {{D}_{1}}}}{{\partial \eta }}\chi \frac{{\partial f}}{{\partial \chi }} \\ = mf\frac{{\partial {{D}_{1}}}}{{\partial \eta }} + \frac{\chi }{{{{\chi }^{{2m}}}}}\frac{\partial }{{\partial \eta }}\left( {G\frac{{\partial {{D}_{1}}}}{{\partial \eta }}} \right) - \chi \frac{{\Lambda {{\tau }_{{\text{0}}}}}}{{\rho v_{\infty }^{{\text{2}}}}}{{\left( {\frac{{{{D}_{1}}}}{{{{T}_{1}}}}} \right)}^{2}} \\ - \chi \frac{{\Lambda \varepsilon {{\tau }_{{\text{0}}}}}}{{\rho v_{\infty }^{{\text{2}}}}}\frac{{{{D}_{1}}}}{{{{T}_{1}}}}\frac{{{{v}_{*}}\nu }}{{Rv_{\infty }^{{\text{2}}}}}{\text{ }}{\text{.}} \\ \end{gathered} $$

(A12)

We still need to decide what various symbols, such as τ₀/ρ$v_{\infty }^{2}$ and ${{v}_{*}}$ν/R$v_{\infty }^{2}$, mean in the context of flow past a flat plate. The form actually used in the computer program in equation (25) is

$$\frac{{\Lambda {{d}^{2}}}}{{{{{(\xi {{R}^{ + }})}}^{2}}}} = \Lambda [{{{\text{(}}d{\text{/}}t{\text{)}}}^{{\text{2}}}}{\text{ + }}\varepsilon {\text{ }}d].$$

(A13)