Theoretical Analysis of Changes in the System’s Composition in the Course of Oxidative Electrolysis of Bromide Solution: pH Dependence

Abstract

Changes in the indicator electrode potential (at zero current) E and (quasi) equilibrium composition of aqueous solution in the anode chamber of the model electrolyzer, which initially contained 0.5 M concentration of bromide anions, provided that the solution was kept at a constant pH and constant (together with the gas phase above it) total number of Br atoms in all its compounds, are calculated. Theoretical analysis was carried out for four different hypotheses regarding the possible extent of electrolysis and the nature of the processes are theoretically analyzed. They are: (1) no formation of bromine compounds with positive oxidation states occurs, i.e., electrolysis only leads to the formation of molecular bromine in its various forms (the dissolved state of Br₂, as well as phases of liquid bromine ${\text{Br}}_{{\text{2}}}^{{{\text{liq}}}}$, and bromine vapor in the gas space above the ${\text{Br}}_{{\text{2}}}^{{{\text{vap}}}}$ solution); (2) oxidation of bromide ions leads to the formation of bromine compounds in its oxidation state up to +1 inclusive; (3) the process proceeds with the formation of both bromate ion (BrO₃^-) and compounds of bromine with lower oxidation states in solution (${\text{Br}}_{{\text{3}}}^{ - },$ ${\text{Br}}_{{\text{5}}}^{ - },$ Br₂, ${\text{Br}}_{{\text{2}}}^{{{\text{liq}}}},$ ${\text{Br}}_{{\text{2}}}^{{{\text{vap}}}},$ BrO^–, HBrO); (4) in addition to the components specified in clause (3), the formation of the perbromate anion $\left( {{\text{BrO}}_{{\text{4}}}^{ - }} \right)$ is also taken into consideration. All electrochemical and chemical reactions involving bromine-containing species have been taken into consideration in the hypothesis framework of the system’s evolution (1), (2), (3), or (4), are assumed to be in a (quasi)equilibrium state. Predictions for all hypotheses (1), (2), (3), or (4) have been compared at three different pH values of the solution (2, 6 and 10 of Br-containing anolyte composition’s evolution in the course of electrolysis.

APPENDIX

The systems compositions will be calculated, basing on thermodynamic equations (А1)–(А16) for the equilibrium electrochemical, chemical, and physical transformations listed in Table 2.

Table 2. Electrochemical, chemical, and physical transformations. Equilibrium equations and values of parameters

In these equations we use the following notation: Х for a Br-containing component in its aqueous solutions (Br^–, Br₂, ${\text{Br}}_{{\text{3}}}^{ - },$ ${\text{Br}}_{{\text{5}}}^{ - },$ HBrO, BrO^–, ${\text{BrO}}_{{\text{3}}}^{ - },$ and ${\text{BrO}}_{{\text{4}}}^{ - }$), {X} for its activity, ${\text{Br}}_{{\text{2}}}^{{{\text{liq}}}}$ and ${\text{Br}}_{{\text{2}}}^{{{\text{vap}}}}$ for the phases of liquid bromine or its vapor, $\left\{ {{\text{Br}}_{{\text{2}}}^{{{\text{vap}}}}} \right\}$ for the bromine vapor activity (in molar concentration units: mol/dm³), V^sol and V^gas for the solution and gas phase volumes, $E_{i}^{^\circ }$ for the standard potential of the corresponding electrochemical reaction, K_i for the equilibrium constant of the corresponding chemical transformation or for the transfer into gas phase (K^vap). The lower index “sat” denotes the system state in which the dissolved bromine and bromide-anion are equilibrated with the liquid bromine phase [equation (А7)], so that {Br₂} = {B_r2}_sat = 0.185 М [21]; the activities of the rest components are determined by the corresponding thermodynamic equations, in particular, equation (А7) for {Br^–}_sat. The entry “log” in this work always means common (decimal) logarithm, in particular, in equations (А1)–(А16) and below. The parameter A = F/(RTln 10) = 16.92 V^–1 (at room temperature).

For the components [X_i] concentrations all equations (А1)–(А16) hold when the components’ activities {X_i} are replaced by [X_i], the standard potential $E_{i}^{^\circ }$ of each reaction is replaced by the apparent potential $E_{i}^{{^\circ {\kern 1pt} '}},$ the transformation equilibrium constant K_i, by the apparent equilibrium constant $K_{i}^{'}$ [18]. Further calculations were carried out under the assumption that the components’ activities in all expressions of Table 2 are replaced by their concentrations; in these equations, we used thermodynamic values of the parameters.

The Method for Determining of Concentrations of the System’s Components (described at length in works [13, 18])

The calculations are carried out for the known values of the solution рН and the solution:gas phase volume ratio (in these calculations we took the ratio V ^gas/V ^sol = 0.8) for one of the chosen values of the potential Е. First, we consider the system’s critical state, that is, such a summary concentration c_tot at which the dissolved bromine concentration (approximately equal to its activity) reaches its value in saturated solution: {Br₂}_sat = 0.185 М, according to equation (А7), whereas the liquid bromine phase is still absent: $\left[ {{\text{Br}}_{{\text{2}}}^{{{\text{liq}}}}} \right]$ = 0. Then equations (А1) or (А7), (А3), (А5), (А6), (А8), (А10), (А13), and (А14) allow calculating the critical concentrations $c_{i}^{*}$ for all other components in the solution, and the effective concentration of bromine as a vapor above the solution. The summing of the concentrations for all components gives the critical value of the summary concentration $c_{{{\text{tot}}}}^{*}.$ When the given value of the Br-atom summary concentration, that is, the bromide initial concentration c_tot, exceeds its critical value: c_tot > $c_{{{\text{tot}}}}^{*},$ then concentrations of all the components (other than liquid bromine) are equal to their critical concentrations $c_{i}^{*}$. And the liquid bromine effective concentration (its amount divided by the solution volume) is 1/2 (c_tot – $c_{{{\text{tot}}}}^{*}$).

More complicated is the mathematical problem related to the case when the Br-atom summary concentration is below its critical value (at given parameters Е and рН): c_tot < $c_{{{\text{tot}}}}^{*}.$ Here the liquid bromine phase does not form, that is $\left[ {{\text{Br}}_{{\text{2}}}^{{{\text{liq}}}}} \right]$ = 0. Then eight equilibrium interrelations between other components’ concentrations (А1), (А3), (А5), (А6), (А8), (А10), (А13), and (А14), combined with equation (14) for the known values of the summary concentration c_tot, potential Е and рН in aggregate give a set of nine nonlinear algebraic equations for nine unknown components’ concentrations, see Table 1 (excluding ${\text{Br}}_{{\text{2}}}^{{{\text{liq}}}}$). By using the method of sequential exclusion of the unknown variables, thise set can be reduced to a quintic equation with respect to the bromide-ion [Br^–] concentration, or that of bromate-ion $\left[ {{\text{BrO}}_{{\text{3}}}^{ - }} \right].$ The former one was used for the further solution, provided the potential Е was below the standard potential of the redox-couple Br^–/${\text{BrO}}_{{\text{3}}}^{ - },$ that is, E < $E_{{\text{3}}}^{^\circ },$ the latter one, at higher potentials. In both cases, we applied the bisection method to a segment of possible values of the measured concentration accurate within 10^–16. From the found solution, by using equation (13) we determined all concentrations, as well as the number of moles of each component N_i; by using equation (10), the summary redox-charge; by using equation (12), the average oxidation degree х.

The calculating of the bromine-atom summary concentration validated the above-discussed calculations’ correctness.

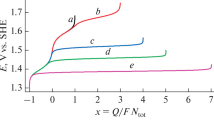
The performing of such calculations (at fixed values of рН and c_tot) for a set of various potential values allows determining the dependence of х on Е (see Fig. 1), as well as the dependence of the system’s composition on the electrode potential Е (Fig. 3) or average oxidation degree х (Fig. 2).