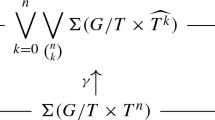Skip to main content
SpringerLink
Log in

Graded Components of the Lie Algebra Associated with the Lower Central Series of a Right-Angled Coxeter Group

  • Research Articles
  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

Abstract

The lower central series of a right-angled Coxeter group \(\mathrm{RC}_{\mathcal K}\) and the corresponding graded Lie algebra \(L(\mathrm{RC}_{\mathcal K})\) associated with the lower central series of a right-angled Coxeter group are studied. Relations are obtained in the graded components of the Lie algebra \(L(\mathrm{RC}_{\mathcal K})\). A basis of the fourth graded component of \(L(\mathrm{RC}_{\mathcal K})\) for groups with at most four generators is described.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Bahri, M. Bendersky, F. R. Cohen, and S. Gitler, “The polyhedral product functor: A method of decomposition for moment–angle complexes, arrangements and related spaces,” Adv. Math. 225 (3), 1634–1668 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  2. V. M. Buchstaber and T. E. Panov, “Torus actions, combinatorial topology, and homological algebra,” Russ. Math. Surv. 55 (5), 825–921 (2000) [transl. from Usp. Mat. Nauk 55 (5), 3–106 (2000)].

    Article  MATH  Google Scholar 

  3. V. M. Buchstaber and T. E. Panov, Toric Topology (Am. Math. Soc., Providence, RI, 2015), Math. Surv. Monogr. 204.

    MATH  Google Scholar 

  4. G. Duchamp and D. Krob, “The lower central series of the free partially commutative group,” Semigroup Forum 45 (3), 385–394 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  5. W. Magnus, A. Karrass, and D. Solitar, Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations (Dover Publ., New York, 1976).

    MATH  Google Scholar 

  6. T. E. Panov and Ya. A. Veryovkin, “Polyhedral products and commutator subgroups of right-angled Artin and Coxeter groups,” Sb. Math. 207 (11), 1582–1600 (2016) [transl. from Mat. Sb. 207 (11), 105–126 (2016)].

    Article  MathSciNet  MATH  Google Scholar 

  7. S. Papadima and A. I. Suciu, “Algebraic invariants for right-angled Artin groups,” Math. Ann. 334 (3), 533–555 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  8. R. R. Struik, “On nilpotent products of cyclic groups,” Can. J. Math. 12, 447–462 (1960).

    Article  MathSciNet  MATH  Google Scholar 

  9. R. R. Struik, “On nilpotent products of cyclic groups. II,” Can. J. Math. 13, 557–568 (1961).

    Article  MathSciNet  MATH  Google Scholar 

  10. Ya. A. Veryovkin, “The associated Lie algebra of a right-angled Coxeter group,” Proc. Steklov Inst. Math. 305, 53–62 (2019) [transl. from Tr. Mat. Inst. Steklova 305, 61–70 (2019)].

    Article  MathSciNet  Google Scholar 

  11. R. D. Wade, “The lower central series of a right-angled Artin group,” Enseign. Math. 61 (3), 343–371 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  12. H. V. Waldinger, “The lower central series of groups of a special class,” J. Algebra 14 (2), 229–244 (1970).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The author is a 2019 Young Russian Mathematics award winner and would like to thank its sponsors and jury. The author also expresses his deep gratitude to his supervisor Taras Panov for the statement of the problem, constant attention, and assistance in the work.

Funding

This work is supported by the Russian Science Foundation under grant no. 21-71-00049, https://rscf.ru/project/21-71-00049/.

Author information

Authors and Affiliations

  1. International Laboratory of Algebraic Topology and Its Applications, Faculty of Computer Science, HSE University, Pokrovskii bul. 11, Moscow, 109028, Russia

    Ya. A. Veryovkin

  2. Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow, 119991, Russia

    Ya. A. Veryovkin

Authors
  1. Ya. A. Veryovkin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ya. A. Veryovkin.

Additional information

Published in Russian in Trudy Matematicheskogo Instituta imeni V.A. Steklova, 2022, Vol. 318, pp. 31–42 https://doi.org/10.4213/tm4287.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Veryovkin, Y.A. Graded Components of the Lie Algebra Associated with the Lower Central Series of a Right-Angled Coxeter Group. Proc. Steklov Inst. Math. 318, 26–37 (2022). https://doi.org/10.1134/S0081543822040034

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543822040034

Search

Navigation