Resonance interaction of breathers in the Manakov system

Abstract

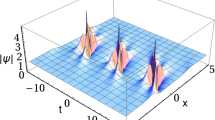
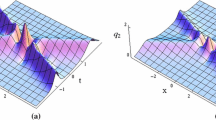
By means of the dressing technique, we build multipole solutions of the focusing Manakov system under a constant background. These solutions become degenerate when the poles of the dressing function merge. We find that with a special choice of the integration constants, such solutions describe the fusion or decay of the pulsing solitons—breathers—and their wave numbers and frequencies satisfy the typical resonance condition. We investigate the different cases of such resonance interactions.

Appendix A. “Dressing” procedure for the defocusing Manakov system on a condensate background

It is instructive to give the result yielded by the “dressing” technique when it is used to construct solutions of the defocusing Manakov system on a condensate background.

The $U$–$V$ pair for the defocusing Manakov system

$$i\,\partial_t\psi_j-\frac{\partial_x^2\psi_j}{2} +\psi_j(|\psi_1|^2+|\psi_2|^2-A^2)=0,\quad j=1,2;\qquad A^2=A_1^2+A_2^2, $$

(A.1)

on a condensate background $|\psi_{1,2}|\to A_{1,2}$ and $x\to\pm\infty$ has the form [15], [16]

$$\partial_x\Phi=U\Phi,\qquad \partial_t\Phi =V\Phi=-\biggl[\lambda U+\frac{iW}{2}\biggr]\Phi,$$

where

$$U=\begin{pmatrix} -i\lambda &\psi_1 &\psi_2 \\ \psi_1^* &i\lambda &0 \\ \psi_2^* &0 &i\lambda \end{pmatrix}, \qquad W=\begin{pmatrix} A^2-|\psi_1|^2-|\psi_2|^2 &\partial_x\psi_1 &\partial_x\psi_2 \\ -\partial_x\psi_1^* &|\psi_1|^2-A^2 &\psi_1^*\psi_2 \\ -\partial_x\psi_2^* &\psi_1\psi_2^* &|\psi_2|^2-A^2 \end{pmatrix}.$$

The “seed” solution is

$$\Phi_0(x,t,\lambda)=[(1-r^2)e^{-\varphi_0}]^{-1/3}\begin{pmatrix} 0 &e^\varphi &-ire^{-\varphi} \\[1mm] -\dfrac{A_2}{A}e^{-\varphi_0} &\dfrac{A_1}{A}ire^\varphi &\dfrac{A_1}{A}e^{-\varphi} \\[3mm] \dfrac{A_1}{A}e^{-\varphi_0} &\dfrac{A_2}{A}ire^\varphi &\dfrac{A_2}{A}e^{-\varphi} \end{pmatrix},$$

where $r=A/(\lambda+\zeta)$, $\zeta=\sqrt{\lambda^2-A^2}$, $\det\Phi_0=1$,

$$\varphi_0(x, t)=-i\lambda x+\frac{i}{2}(\lambda^2+\zeta^2)t,\qquad \varphi(x, t)=-i\zeta x+i\lambda\zeta t.$$

The matrices $U$ and $V$ satisfy the reduction

$$U(\lambda)=-JU^\dagger(\lambda^*)J,\qquad V(\lambda)=-JV^\dagger(\lambda^*)J,$$

where $J$ is a $3 \times 3$ analogue of $\sigma_3$: $J\equiv\operatorname{diag}(1,-1,-1)$. We set $\varphi_0^*(\lambda^*)=-\varphi_0(\lambda)$ and $\varphi^*(\lambda^*)=-\varphi(\lambda)$. Then

$$\Phi^{-1}(\lambda)=[J\Phi(\lambda^*)J]^\dagger.$$

The “dressing” function $\chi=\Phi\Phi_0^{-1}$ satisfies the asymptotic conditions

$$\chi(\lambda)=E+\frac{R}{\lambda}+O\biggl(\frac{1}{\lambda^2}\biggr),\qquad |\lambda|\to\infty,$$

and the reduction

$$\chi^{-1}(\lambda)=[J\chi(\lambda^*)J]^\dagger.$$

We choose the one-pole solution in the form

$$\chi(\lambda)=E+\frac{R}{\lambda-\lambda_1},$$

where $E$ is the unit matrix. Then, similarly to the scalar case, we obtain

$$R=\begin{pmatrix} p_1q_1 &-p_1q_2 &-p_1q_3 \\ p_2q_1 &-p_2q_2 &-p_2q_3 \\ p_3q_1 &-p_3q_2 &-p_3q_3 \end{pmatrix},$$

where

$$\mathbf p=\frac{\mathbf q^*(\lambda_1-\lambda_1^*)}{|q_1|^2-|q_2|^2-|q_3|^2},\qquad \mathbf q=\Phi_0^*(x,t,\lambda_1^*)\mathbf c,\qquad \det\chi(\lambda)=\frac{\lambda-\lambda_1^*}{\lambda-\lambda_1},$$

and $\mathbf C$ is an arbitrary complex constant vector. Here, we redefine the vector $\mathbf q$ by eliminating the scalar factor $[(1-r^2)e^{-\varphi_0}]^{-1/3}$ from its components.

As a result, the solution $\psi_{1,2}(x,t)$ becomes

$$\begin{aligned} \, &\psi_j(x,t)=A_j-2ip_1q_{j+1} =A_j-\frac{2iq_1^*q_{j+1}(\lambda_1-\lambda_1^*)}{|q_1|^2-|q_2|^2-|q_3|^2},\qquad j=1,2; \\ &q_1=e^{-\varphi}C_1+ir^*e^\varphi C_2,\qquad q_2=-\frac{A_2}{A}e^{\varphi_0}C_0 -\frac{A_1}{A}ir^*e^{-\varphi}C_1+\frac{A_1}{A}e^\varphi C_2, \\ &q_3=\frac{A_1}{A}e^{\varphi_0}C_0 -\frac{A_2}{A}ir^*e^{-\varphi}C_1+\frac{A_2}{A}e^\varphi C_2, \end{aligned}$$

(A.2)

where $C_0$, $C_1$, and $C_2$ are arbitrary complex constants, $\varphi\equiv u+iv$, and $\varphi_0\equiv u_0+iv_0$.

We use the parameterization

$$\lambda_1=A\cosh(\xi+i\alpha),\qquad \lambda_1-\lambda_1^*=2iA\sin\alpha\sinh\xi,\qquad \zeta=A\sinh(\xi+i\alpha),\qquad r=e^{-\xi-i\alpha},$$

$\xi>0$, $0\le\alpha\le\pi$, and study the structure of solution (A.2), assuming that one of the integration constant is zero. From (A.2) with $C_0=0$, we then obtain a generalization of soliton [27]—a singular solution of the scalar defocusing NLSE, multiplied by the vector $(A_1,A_2)/A$. The denominator of this solution vanishes at some point of the $(x,t)$ plane, and the solution itself has a simple pole at this point. Similar excitations were studied in [28]

At $C_1=0$, the denominator in (A.2) is sign-definite:

$$|q_1|^2-|q_2|^2-|q_3|^2=-e^{-\xi+2u}[2|C_2|^2\sinh\xi+|C_0|^2e^{2(u_0-u)+\xi}]<0,$$

In this case, we obtain a soliton of the vector defocusing NLSE [15]. At $C_2=0$, the denominator

$$|q_1|^2-|q_2|^2-|q_3|^2=-e^{-\xi-2u}[-2|C_1|^2\sinh\xi+|C_0|^2e^{2(u_0+u)+\xi}]$$

is not sign-definite. The corresponding solution represents a “singular analogue” of the soliton of the vector defocusing NLSE.

Thus, proceeding by analogy with the case of the vector focusing NLSE, we conclude that at arbitrary integration constants, solution (A.2) describes the fusion of a soliton with a singular excitation into a new singular excitation or, conversely, the decay of a singular solution into another singular solution and a soliton. It can be verified directly that both processes are resonance ones. That is, the frequencies and the wave numbers 1, 2, and 3 of solution (A.2) satisfy the resonance condition

$$\omega_3=\omega_1+\omega_2,\qquad p_3=p_1+p_2.$$

The corresponding values

$$\begin{alignedat}{2} &p_1=2A\sinh\xi\cos\alpha,&\qquad &\omega_1=A^2\sinh(2\xi)\cos(2\alpha), \\ &p_2=Ae^{-\xi}\cos\alpha,&\qquad &\omega_2=A^2\frac{e^{-2\xi}}{2}\cos(2\alpha), \\ &p_3=Ae^\xi\cos\alpha, &\qquad &\omega_3=A^2\frac{e^{2\xi}}{2}\cos(2\alpha) \end{alignedat}$$

can be found from the expressions

$$2v=-p_1x+\omega_1t,\qquad v_0-v=-p_2x+\omega_2t, \qquad v_0+v=-p_3x+\omega_3t.$$

We thus arrive at the resonance interaction of the solutions of model (A.1) in a class of nonintegrable functions.