Andreev states in a quasi-one-dimensional superconductor on the surface of a topological insulator

Abstract

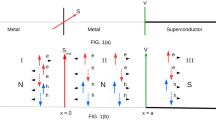
We study bound states in an s-wave superconducting strip on the surface of a topological superconductor with the perpendicular Zeeman field. We prove analytically that an arbitrarily small local perturbation of the Zeeman field generates Andreev bound states with energies near the superconducting gap edges, while the (nonmagnetic) impurity potential does not produce such an effect. Rather large perturbations of the Zeeman field can lead to the appearance of Andreev bound states with energies near zero. We analytically find wave functions of the Andreev bound states under consideration. In contrast to the one-dimensional case, the wave functions do not satisfy the conjugation conditions that are characteristic of Majorana states because of the influence of neighboring subbands.

Appendix

To find the Green’s function of the Hamiltonian $H^{(n)}$, we find the function $\Psi$ from the equation $(H^{(n)}-E)\Psi=\Phi$. We rewrite this equation in the form

$$\begin{aligned} \, &\begin{pmatrix} M-E & -i\partial_x+2\pi in/W & 0 & \Delta\\ -i\partial_x-2\pi in/W & -M-E & -\Delta & 0\\ 0 & -\Delta & -M-E & -i\partial_x-2\pi in/W \\ \Delta & 0 & -i\partial_x+2\pi in/W & M-E \end{pmatrix} \times{} \\ &\qquad\times \begin{pmatrix} \psi _{\mathrm{e}\uparrow}^{(n)}(x)\\[1mm] \psi _{\mathrm{e}\downarrow}^{(n)}(x)\\[1mm] \psi _{\mathrm{h}\uparrow}^{(n)}(x) \\[1mm] \psi _{\mathrm{h}\downarrow}^{(n)}(x) \end{pmatrix}= \begin{pmatrix} \varphi_{\mathrm{e}\uparrow}^{(n)}(x)\\[1mm] \varphi_{\mathrm{e}\downarrow}^{(n)}(x)\\[1mm] \varphi_{\mathrm{h}\uparrow}^{(n)}(x) \\[1mm] \varphi_{\mathrm{h}\downarrow}^{(n)}(x) \end{pmatrix} \end{aligned}$$

or, after the Fourier transformation,

$$\begin{aligned} \, &\widetilde{\varphi}(p)=F\varphi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-ipx}\varphi(x)\,dx, \nonumber \\ &\begin{pmatrix} M-E & p+2\pi in/W & 0 & \Delta\\[1mm] p-2\pi in/W & -M-E & -\Delta & 0\\[1mm] 0 & -\Delta & -M-E & p-2\pi in/W \\[1mm] \Delta & 0 & p+2\pi in/W & M-E \end{pmatrix} \begin{pmatrix} \widetilde{\psi} _{\mathrm{e}\uparrow}^{(n)}(p)\\[1mm] \widetilde{\psi} _{\mathrm{e}\downarrow}^{(n)}(p)\\[1mm] \widetilde{\psi} _{\mathrm{h}\uparrow}^{(n)}(p) \\[1mm] \widetilde{\psi} _{\mathrm{h}\downarrow}^{(n)}(p) \end{pmatrix} ={} \nonumber \\ &\qquad=(\widetilde{\varphi}_{\mathrm{e}\uparrow}^{(n)}(p), \widetilde{\varphi}_{\mathrm{e}\downarrow}^{(n)}(p), \widetilde{\varphi}_{\mathrm{h}\uparrow}^{(n)}(p), \widetilde{\varphi}_{\mathrm{h}\downarrow}^{(n)}(p))^{\mathrm T}. \end{aligned}$$

(A.1)

The determinant of the matrix in (A.1) is

$$\begin{aligned} \, d={}&\biggl(p^2+\biggl(\frac{2\pi n}{W}\biggr)^2\biggr)^2 +2\biggl(p^2+\biggl(\frac{2\pi n}{W}\biggr)^2\biggr)(M^2+\Delta ^2-E^2)+{} \nonumber \\ &+(M^2-E^2)^2-2\Delta ^2(M^2+E^2)+\Delta ^4. \end{aligned}$$

(A.2)

From (A.2), we find the dispersion law for the $n$th subband

$$ E^2=(M\pm \Delta)^2+p^2+\biggl(\frac{2\pi n}{W}\biggr)^2$$

(A.3)

and the equality

$$\begin{aligned} \, \frac{1}{d}=&-\frac{1}{4M\Delta}\biggl( \frac{1}{p^2+(2\pi n/W)^2+(M+\Delta)^2-E^2}-{} \nonumber \\ &-\frac{1}{p^2+(2\pi n/W)^2+(M-\Delta)^2-E^2}\biggr). \end{aligned}$$

(A.4)

Using Cramer’s rule and neglecting quantities of the order of smallness of $(M-\Delta)^2$, we obtain the Green’s function of the Hamiltonian $H^{(n)}$ in momentum representation,

$$\begin{aligned} \, \widetilde{G}^{(n)}(p,p',E)={}&\frac{\delta(p-p')}{2}\biggl(\frac {1}{p^2-a_n^2}-\frac{1}{p^2-b_n^2}\biggr)\times{} \nonumber \\ &\times \begin{pmatrix} M-\Delta+E & p+2\pi i n/W & -(p+2\pi i n/W) & -(M-\Delta+E)\\ p-2\pi i n/W & -(M-\Delta-E) & M-\Delta-E & -(p-2\pi i n/W)\\ -(p-2\pi i n/W) & M-\Delta-E & -(M-\Delta-E) & p-2\pi i n/W\\ -(M-\Delta+E) & -(p+2\pi i n/W) & p+2\pi i n/W & M-\Delta+E\\ \end{pmatrix}, \end{aligned}$$

(A.5)

where $a_n^2=E^2-(2\pi n/W)^2-(M-\Delta)^2$ and $b_n^2=E^2-(2\pi n/W)^2-(M+\Delta)^2$. To pass to the coordinate representation, we use the known formulas

$$ \begin{aligned} \, &\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \frac{e^{ipx}\widetilde{\varphi}(p)\,dp}{p^2-a^2}= -\frac{1}{2ia}\int_{-\infty}^{\infty} e^{ia|x-x'|}\varphi(x')\,dx', \\[1mm] &\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \frac{p e^{ipx}\widetilde{\varphi}(p)\,dp}{p^2-a^2}= -\frac{1}{2i}\int_{-\infty}^{\infty} e^{ia|x-x'|}\operatorname{sgn}(x-x')\varphi(x')\,dx', \end{aligned}$$

(A.6)

assuming that $a=a_n$ or $b_n$.

To find the Green’s function in the coordinate representation using formulas (A.6), we integrate equalities (A.5) over $p$. Because of the conditions for the quantities $1/W$ and $|M-\Delta |$ (see Sec. 2), when integrating over the region where the $p$ are small, the denominator of the second term in the factor before the matrix in (A.5) is much larger than that of the first term, and the integrals over the region where $p$ are rather large are small. Thus, the second term in (A.5) can be neglected. Although the remaining integrals are taken over the entire number line, the smallness of their denominators for small $p$ under the adopted conditions for the parameters makes these integrals mainly saturated by small $p$, and the condition for the smallness of the momenta $p$ (see the assumptions after (11)) is satisfied. This reasoning is easily confirmed by numerical estimations.

Based on the foregoing, we use (A.5) and (A.6) to obtain the Green’s function of the Hamiltonian $H^{(n)}$ in the coordinate representation:

$$\begin{aligned} \, &{G}^{(n)}(x-x',E)=-\frac{e^{ia_n|x-x'|}}{4ia_n} \begin{pmatrix} M-\Delta+E & b_n^+ & -b_n^+ & -(M-\Delta+E)\\ b_n^- & -(M-\Delta-E) & M-\Delta-E & -b_n^-\\ -b_n^- & M-\Delta-E & -(M-\Delta-E) & b_n^-\\ -(M-\Delta+E) & -b_n^+ & b_n^+ & M-\Delta+E\\ \end{pmatrix}, \end{aligned}$$

(A.7)

where $b_n^\pm=a_n \operatorname{sgn}(x-x')\pm 2\pi i n/W$.