Abstract
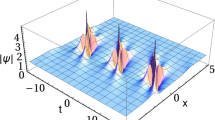
We present a one-line closed-form expression for the three-parameter breather of the nonlinear Schrödinger equation. This provides an analytic proof of the time period doubling observed in experiments. The experimental check that some pulses generated in optical fibers are indeed such generalized breathers will be drastically simplified.
Similar content being viewed by others
Notes
The scaling invariance \((x,t,A)\to(kx,k^2t,kA)\) of the NLS equation reduces this number by one.
We never use the ambiguous term “periodic” for elliptic solutions, but always either “doubly periodic,” alias “elliptic” (example: Jacobi \(\operatorname{dn}\), Weierstrass \(\wp\)), or “quasi-doubly periodic,” alias “quasielliptic,” alias “elliptic of the second kind” in Hermite’s terminology [11, Vol. 1, p. 227; Vol. 2, p. 506] (example: the solution \(\mathrm{H}(t,a)\) of Lamé equation (10)).
To convert to the notation of Jacobi, see [21], § 18.9.11 and 18.10.8.
Under the addition of any of the two periods, a quasielliptic function is multiplied by a constant factor, the multiplier.
References
V. I. Bespalov and V. I. Talanov, “Filamentary structure of light beams in nonlinear liquids,” JETP Lett., 3, 307–310 (1966).
V. E. Zakharov, “Stability of periodic waves of finite amplitude on the surface of a deep fluid,” J. Appl. Mech. Tech. Phys., 9, 190–194 (1968).
N. Akhmediev, A. Ankiewicz, and M. Taki, “Waves that appear from nowhere and disappear without a trace,” Phys. Lett. A, 373, 675–678 (2009).
V. V. Konotop and M. Salerno, “Modulational instability in Bose–Einstein condensates in optical lattices,” Phys. Rev. A, 65, 021602, 4 pp. (2002); arXiv: cond-mat/0106228.
P. J. Everitt, M. A. Sooriyabandara, M. Guasoni et al., “Observation of a modulational instability in Bose–Einstein condensates,” Phys. Rev. A, 96, 041601, 5 pp. (2017); arXiv: 1703.07502.
D. R. Solli, C. Ropers, P. Koonath, and B. Jalali, “Optical rogue waves,” Nature, 450, 1054–1057 (2007).
D.-I. Yeom and B. J. Eggleton, “Rogue waves surface in light,” Nature, 450, 953–954 (2007).
E. A. Kuznetsov, “On solitons in parametrically unstable plasma,” Sov. Phys. Dokl., 22, 507–508 (1977).
N. N. Akhmediev and V. I. Korneev, “Modulation instability and periodic solutions of the nonlinear Schrödinger equation,” Theoret. and Math. Phys., 69, 1089–1093 (1986).
N. N. Akhmediev, V. M. Eleonskii, and N. E. Kulagin, “Exact first-order solutions of the nonlinear Schrödinger equation,” Theoret. and Math. Phys., 72, 809–818 (1987).
G. H. Halphen, Traité des fonctions elliptiques et de leurs applications, Vol. 1: Théorie des fonctions elliptiques et de leurs développements en série, Gauthier-Villars, Paris (1886); Vol. 2: Applications à la mécanique, à la physique, à la géodésie, à la géométrie et au calcul intégral (1888); Vol. 3: Fragments (1891).
G. Vanderhaegen, P. Szriftgiser, C. Naveau et al., “Observation of doubly periodic solutions of the nonlinear Schrödinger equation in optical fibers,” Optics Lett., 45, 3757–3760 (2020).
M. Conforti, A. Mussot, A. Kudlinski, S. Trillo, and N. Akhmediev, “Doubly periodic solutions of the focusing nonlinear Schrödinger equation: recurrence, period doubling, and amplification outside the conventional modulation-instability band,” Phys. Rev. A, 101, 023843, 11 pp. (2020).
N. Akhmediev and A. Ankiewicz, “First-order exact solutions of the nonlinear Schrödinger equation in the normal-dispersion regime,” Phys. Rev. A, 47, 3213–3221 (1993).
D. Mihalache and N. C. Panoiu, “Exact solutions of nonlinear Schrödinger equation for positive group velocity dispersion,” J. Math. Phys., 33, 2323–2328 (1992).
D. Mihalache and N. C. Panoiu, “Exact solutions of the nonlinear Schrödinger equation for the normal-dispersion regime in optical fibers,” Phys. Rev. A, 45, 6730–6734 (1992).
K. W. Chow, “A class of doubly periodic waves for nonlinear evolution equations,” Wave Motion, 35, 71–90 (2002).
D. V. Chudnovsky, G. V. Chudnovsky, and M. Tabor, “Painlevé property and multicomponent isospectral deformation equations,” Phys. Lett. A, 97, 268–274 (1983).
R. Conte and M. Musette, The Painlevé Handbook (Mathematical Physics Studies), Springer, Cham (2020).
G.-H. Halphen, “Mémoire sur la réduction des équations différentielles linéaires aux formes intégrables,” Mém. Acad. Sci. Inst. France, 28, 1–301 (1884).
M. Abramowitz and I. A. Stegun (eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (National Bureau of Standards Appl. Math. Ser., Vol. 55), Dover, New York (1972).
L. Kiepert, “Auflösung der Transformationsgleichungen und Division der elliptischen Functionen,” J. Reine Angew. Math., 1873, 34–44 (1873).
K. W. Chow, R. Conte, and N. Xu, “Analytic doubly periodic wave patterns for the integrable discrete nonlinear Schrödinger (Ablowitz–Ladik) model,” Phys. Lett. A, 349, 422–429 (2006); arXiv: nlin/0509005.
T. Kawata and H. Inoue, “Inverse scattering method for the nonlinear evolution equations under nonvanishing conditions,” J. Phys. Soc. Japan, 44, 1722–1729 (1978).
Y.-C. Ma, “The perturbed plane-wave solutions of the cubic Schrödinger equation,” Stud. Appl. Math., 60, 43–58 (1979).
M. A. Alejo, L. Fanelli, and C. Muñoz, “The Akhmediev breather is unstable,” São Paulo J. Math. Sci., 13, 391–401 (2019).
D. H. Peregrine, “Water waves, nonlinear Schrödinger equations and their solutions,” J. Austral. Math. Soc. Ser. B, 25, 16–43 (1983).
V. E. Zakharov and A. B. Shabat, “Interaction betweem solitons in a stable medium,” Soviet Phys. JETP, 37, 823–828 (1973).
V. E. Zakharov and A. B. Shabat, “Exact theory of two-dimensional self-focusing and onedimensional self-modulation of waves in nonlinear media,” JETP, 34, 62–69 (1972).
K. W. Chow, “Solitary waves on a continuous background,” J. Phys. Soc. Japan, 64, 1524–1528 (1995).
Acknowledgments
The author is pleased to thank Micheline Musette for a critical reading of the manuscript.
Funding
This work was initiated at the Centre International de Rencontres Mathématiques, Marseille (grant 2311, year 2019), whose hospitality is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The author declares no conflicts of interest.
Additional information
Translated from Teoreticheskaya i Matematicheskaya Fizika, 2021, Vol. 209, pp. 46–58 https://doi.org/10.4213/tmf10095.
Rights and permissions
About this article
Cite this article
Conte, R. Explicit breather solution of the nonlinear Schrödinger equation. Theor Math Phys 209, 1357–1366 (2021). https://doi.org/10.1134/S0040577921100032
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0040577921100032