Abstract
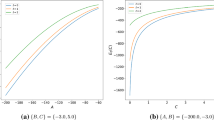
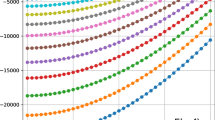
We use the tridiagonal representation approach to enlarge the class of exactly solvable quantum systems. For this, we use a square-integrable basis in which the matrix representation of the wave operator is tridiagonal. In this case, the wave equation becomes a three-term recurrence relation for the expansion coefficients of the wave function with a solution in terms of orthogonal polynomials that is equivalent to a solution of the original problem. We obtain S-wave bound states for a new four-parameter potential with a 1/r2 singularity but short-range, which has an elaborate configuration structure and rich spectral properties. A particle scattered by this potential must overcome a barrier and can then be trapped in the potential valley in a resonance or bound state. Using complex rotation, we demonstrate the rich spectral properties of the potential in the case of a nonzero angular momentum and show how this structure varies with the parameters of the potential.
Similar content being viewed by others
References
G. A. Natanzon, “General properties of potentials for which the Schrödinger equation can be solved by means of hypergeometric functions,” Theor. Math. Phys., 38, 146–153 (1979).
R. De, R. Dutt, and U. Sukhatme, “Mapping of shape invariant potentials under point canonical transformations,” J. Phys. A: Math. Gen., 25, L843–L850 (1992).
A. M. Ishkhanyan, “Schrödinger potentials solvable in terms of the confluent Heun function,” Theor. Math. Phys., 188, 980–993 (2016).
A. D. Alhaidari, “An extended class of L2-series solutions of the wave equation,” Ann. Phys., 317, 152–174 (2005).
A. D. Alhaidari, “Analytic solution of the wave equation for an electron in the field of a molecule with an electric dipole moment,” Ann. Phys., 323, 1709–1728 (2008).
A. D. Alhaidari and H. Bahlouli, “Extending the class of solvable potentials: I. The infinite potential well with a sinusoidal bottom,” J. Math. Phys., 49, 082102 (2008).
A. D. Alhaidari, “Extending the class of solvable potentials: II. Screened Coulomb potential with a barrier,” Phys. Scr., 81, 025013 (2010); arXiv:1004.3905v1 [math-ph] (2010).
H. Bahlouli and A. D. Alhaidari, “Extending the class of solvable potentials: III. The hyperbolic single wave,” Phys. Scr., 81, 025008 (2010).
A. D. Alhaidari, “Solution of the nonrelativistic wave equation using the tridiagonal representation approach,” J. Math. Phys., 58, 072104 (2017).
R. Koekoek and R. F. Swarttouw, “The Askey-scheme of hypergeometric orthogonal polynomials and its qanalogues,” Reports of the Faculty of Technical Mathematics and Informatics, No. 98–17, Delft Univ. of Technology, Delft, 38–44 (1998); arXiv:math/9602214v1 (1996).
A. D. Alhaidari and M. E. H. Ismail, “Quantum mechanics without potential function,” J. Math. Phys., 56, 072107 (2015).
K. M. Case, “Orthogonal polynomials from the viewpoint of scattering theory,” J. Math. Phys., 15, 2166–2174 (1974).
J. S. Geronimo and K. M. Case, “Scattering theory and polynomials orthogonal on the real line,” Trans. Amer. Math. Soc., 258, 467–494 (1980).
A. D. Alhaidari, “Representation reduction and solution space contraction in quasi-exactly solvable systems,” J. Phys. A: Math. Theor., 40, 6305–6328 (2007).
R. W. Haymaker and L. Schlessinger, “Padé approximants as a computational tool for solving the Schrodinger and Bethe–Salpeter equations,” in: The Padé Approximation in Theoretical Physics (Math. in Sci. and Engineering, Vol. 71, G. A. Baker and J. L. Gammel, eds.), Acad. Press, New York (1970), pp. 257–287.
J. Aquilar and J. M. Combes, “A class of analytic perturbations for one-body Schrödinger Hamiltonians,” Commun. Math. Phys., 22, 269–279 (1971).
E. Balslev and J. M. Combes, “Spectral properties of many-body Schrödinger operators with dilatation-analytic interactions,” Commun. Math. Phys., 22, 280–294 (1971).
B. Simon, “Quadratic form techniques and the Balslev–Combes theorem,” Commun. Math. Phys., 27, 1–9 (1972).
B. Simon, “Resonances in n-body quantum systems with dilatation analytic potentials and the foundations of time-dependent perturbation theory,” Ann. Math., 97, 247–274 (1973).
C. Cerjan, R. Hedges, C. Holt, W. P. Reinhardt, K. Scheibner, and J. J. Wendoloski, “Complex coordinates and the Stark effect,” Internat. J. Quantum Chem., 14, 393–418 (1978).
W. P. Reinhardt, “Complex coordinates in the theory of atomic and molecular structure and dynamics,” Ann. Rev. Phys. Chem., 33, 223–255 (1982).
B. R. Junker, “Recent computational developments in the use of complex scaling in resonance phenomena,” Adv. Atom. Mol. Phys., 18, 207–263 (1982).
A. Maquet, S.-I. Chu, and W. P. Reinhardt, “Stark ionization in dc and ac fields: An L2 complex-coordinate approach,” Phys. Rev. A, 27, 2946–2970 (1983).
Y. K. Ho, “The method of complex coordinate rotation and its applications to atomic collision processes,” Phys. Rep., 99, 1–68 (1983).
M. Bylicki, “Methods involving complex coordinates applied to atoms,” Adv. Quantum Chem., 32, 207–226 (1998).
N. Moiseyev, “Quantum theory of resonances: calculating energies, widths, and cross-sections by complex scaling,” Phys. Rep., 302, 212–293 (1998).
Author information
Authors and Affiliations
Corresponding author
Additional information
Prepared from an English manuscript submitted by the author; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, Vol. 195, No. 3, pp. 422–436, June, 2018.
Rights and permissions
About this article
Cite this article
Alhaidari, A.D. Four-Parameter 1/r2 Singular Short-Range Potential with Rich Bound States and A Resonance Spectrum. Theor Math Phys 195, 861–873 (2018). https://doi.org/10.1134/S0040577918060053
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0040577918060053