Internal Structure of Venus Based on the PREM Model

Abstract—

Models of the internal structure of Venus have been constructed with a wide range of crustal thickness (30–70 km) and core radius (2800–3500 km). An analysis of the pressure values in the center of the planet allows us to conclude that the presence of a solid inner core is unlikely if the composition and temperature profile of Venus correspond to that of the Earth. Andrade’s rheology was used to take into account the inelasticity of the interior of Venus when calculating the tidal Love numbers and the angle of delay of the tidal hump. Comparison of experimental values of the Love number k₂ with the model gives the radius of the core of Venus in the range of 3100–3500 km. It is shown that to determine the characteristic viscosity of the Venusian mantle, the key factor is the determination of the angle of retardation of the tidal bulge: values of 0.9° correspond to low viscosity and high temperature, and 0.4° to high viscosity and low temperature, so the planned measurements of tidal parameters and the moment of inertia of the planet in the VERITAS and EnVision missions will be able to impose restrictions on the distribution of viscosity and temperature in the interior of Venus.

INTRODUCTION

The processes occurring in the mantles and cores of planets are closely related to their evolution (O’Rourke et al., 2023). Despite the fact that Venus and the Earth are similar in such parameters as mass and radius, the evolutionary development of the planets followed different scenarios, and Venus remains one of the most mysterious planets. To understand the reasons for the difference in evolutionary processes, it is necessary to know the internal structure of Venus.

In this work, we assume that Venus and the Earth are close in chemical composition, which does not contradict modern ideas. Therefore, when constructing a model of the internal structure of Venus, it makes sense to use the parameters of the PREM (Preliminary Reference Earth Model) (Dziewonski and Anderson, 1981), the most commonly used model, as a first approximation for constructing regional and three-dimensional modern earth models. PREM is a spherically symmetric model of the Earth, which shows the distributions along the radius of density, seismic wave velocities, elastic models (compression modulus K and shear modulus μ), pressure, acceleration of gravity and other physical quantities.

Usually, when building a model of the internal structure of the planet, we rely on data on topography and the gravitational field: mass, average radius, moment of inertia, and tidal Love number k₂. In the absence of seismic data, the moment of inertia is one of the main constraints on the radial density distribution in the model. Determining the moment of inertia requires measuring the rate of precession, and the difficulty lies in the fact that the value of the constant precession is very small ∼ 2 × 10^–5 (Zharkov and Gudkova, 2019). Recently, from measurements from the Earth with two radio telescopes located in the United States, and using estimates of the precession rate, a single experimental value of the polar moment of inertia was obtained for Venus, which is 0.337 ± 0.024 (Margot et al., 2021). The rate of precession of the Venusian axis of rotation is planned to be determined in the EnVision mission (Rosenblatt et al., 2021). At present, a sufficiently large measurement error of the moment of inertia does not allow imposing strict restrictions on models of the internal structure of the planet.

The quantities that make it possible to control both the density distribution and the distribution of elastic parameters in the interior of the planet are the tidal Love numbers. Love numbers (Love, 1909) characterize how much the surface of the planet is displaced under the influence of tidal forces (number h), and how the gravitational field of the planet changes due to the redistribution of mass in it due to the action of tidal forces (number k). According to the observations of variations in the gravitational field of Venus onboard the Magellan and PioneerVenusOrbiter spacecraft, the value of the tidal Love number is known k₂ = 0.295 ± 0.066 (Konopliv and Yoder, 1996), which is measured from the solar tide on Venus (the period is 58.4 days). Due to the insufficient accuracy of estimating the range of values of the tidal Love number k₂ and the lack of data on the viscosity in its interior, the discussion continues on whether the core of the planet is in a liquid or solid state, and whether there is an inner solid core (Dumoulin et al., 2017). Despite the rather high measurement error, the value of the Love number k₂, as will be shown below, allows us to impose some restrictions on models of the internal structure of Venus.

When interpreting the value k₂ there are certain difficulties, since knowledge of the inelastic properties of the interior of Venus is required. The value of k₂ measured at a tidal wave period of 58.4 days and depends on the inelasticity of the interior. When building a model of the internal structure, the elastic value of k₂ is calculated, therefore, it is necessary to take into account the rheology of the interior in the period of tidal deformation.

The question of the distribution of viscosity is very complex, and has not been fully resolved even for the Earth. Viscosity estimates for Venus are assumed to be of the same order of magnitude as for the core and mantle of the Earth. For the molten outer core of the Earth, the viscosity estimate is η << 10⁸ Pa s, according to P-wave attenuation data. If the viscosity were about 10⁸ Pa s, then when passing through the core, the P-waves would be attenuated much more strongly than is observed according to seismological data (Zharkov, 2013). The theoretical estimates given in (Zharkov, 2012) show that the viscosity in the outer core should be less than 0.1 Pa s. This value is used in many works, and to calculate the viscoelastic Love number, the viscosity in the outer core is usually neglected (for example, Xiao et al., 2020), since the viscosity in the mantle is much higher by orders of magnitude.

For a perfectly elastic body, the viscosity is equal to infinity, and the medium does not have the property of fluidity. In reality, the medium is not ideal, due to the presence of point and line defects in solid polycrystals, they are capable of slow inelastic deformations, while the viscosity of the medium strongly depends on temperature. Modern studies (e.g., Harig et al., 2010; Čížková et al., 2012) give values for the viscosity in the upper mantle ~10²⁰ Pa s, in the transition zone ~10²¹–10²² Pa with, and at the bottom ~10²²–10²³Pa s. In the Earth’s lithosphere, the viscosity varies from 10¹⁷–10²⁴ Pa s depending on depth and region (Bills et al., 1994; Yaolin and Jianling, 2008). Below, we apply these estimates to the distribution of viscosity in the interior of Venus.

A number of models of the internal structure of Venus were constructed using the parametric Earth model PEM (Dziewonski et al., 1975) as the base (Zharkov et al., 1981; Zharkov and Zasursky, 1982; Kozlovskaya, 1982; Yoder, 1995; Mocquet et al., 2011; Aitta, 2012). It was noted in (Zharkov and Zasursky, 1982) that it is reasonable to take the equation of state for the Earth as the initial equation of state for Venus, since this allows us to automatically take into account the temperature distribution in the interior of the planet, which, most likely, is close to the geothermal at depths greater than 200 km.

The question of the thickness of the Venusian crust is being revised downward based on the analysis of the latest data on the gravitational field and topography (Jiménez-Díaz et al., 2015; O’Rourke and Korenaga, 2015; Yang et al., 2016). In (Gudkova and Zharkov, 2020), models of the internal structure of Venus were built based on PEM models of the Earth for various crustal thicknesses (30–100 km) at a density of 2800 kg/m³, while the mantle density as a function of pressure ρ_m(p) was given by introducing the coefficient A: p_m(p) = Ap_m0(p), where ρ_m0(p) is the equation of state for the Earth. To fulfill the condition of conservation of the mass of the planet: if the core is large (with a radius of 3400–3500 km), then the mantle must be “lighter” (A < 1), and vice versa, if the core is small (with a radius of 2800–2900 km), then the mantle should be “heavier” (A > 1). The composition of the mantle changes as a result of a change in the molar fraction of iron relative to magnesium. With a coefficient A less than unity the iron content in mantle silicates is less than in the adopted basic model. Below, we will use the same approach.

There is a low-viscosity layer in the Earth due to the temperature approaching the melting point, this is taken into account in the Earth’s PREM model, and in this paper we assume the presence of such a layer in the interior of Venus. Uncertainties in the temperature distribution in the interior of Venus (Steinberger et al., 2010; Armann and Tackley, 2012) leave open the question of whether the core of Venus is liquid or solid. In (Dumoulin et al., 2017; Shah et al., 2022) it was shown that, based on the data available to date, the possibility of a solid inner core of Venus cannot be ruled out. However, as in many modern models, in this work we assume that the core is completely melted. The results obtained below justify this assumption.

The outline of the article is as follows. First, elastic models of the internal structure of Venus based on the Earth’s PREM model will be considered. Then, using Andrade’s rheology, models are built taking into account viscoelasticity in the interior of Venus, and it is demonstrated how this affects the values of the model Love numbers. In conclusion, possible limitations on the distribution of viscosity and temperature in the model of the internal structure of Venus are discussed after refining the moment of inertia, Love numbers, and measuring the angle of lag of the tidal bulge in the planned VERITAS (Cascioli et al., 2021) and EnVision (Rosenblatt et al., 2021) missions.

MODELS OF THE INTERNAL STRUCTURE OF VENUS

Elastic Models

The observational data used in building models of the internal structure of Venus are given in the table: mass M₀, average radius R, average density ρ₀, dimensionless moment of inertia I/M₀R², tidal Love number k₂ and pressure on the surface of the planet. The mass of Venus is 81% of the mass of the Earth, and the radius is 320 km less. The average density of Venus is less than that of the Earth, and the moment of inertia is greater. This indicates that the matter in the interior of Venus is less compressed.

Table 1.   Observational data for Venus (M_E is the mass of the Earth, R_E is the radius of the Earth)

The calculation of models of the internal structure of planets is based on the use of the mass equation and the hydrostatic equilibrium equation (see, for example, Zharkov and Trubitsyn, 1980). In dimensionless variables x = r/R, m = M(r)/M₀, ρ = ρ(r)/ρ₀, p = p(r)/p₀, Where ${{p}_{0}} = \frac{{GM_{0}^{2}}}{{4\pi {{{\text{R}}}^{{\text{4}}}}}}$, ${{\rho }_{0}} = \frac{{3{{M}_{0}}}}{{4\pi {{{\text{R}}}^{{\text{3}}}}}}$ the system of equations takes the form:

$$\frac{{dm}}{{dx}} = 3{{x}^{2}}\rho (p),\,\,\,\,\frac{{dp}}{{dx}} = - 3\frac{m}{{{{x}^{2}}}}\rho (p).$$

(1)

In this case, the boundary conditions have the form:

$$m(1) = 1,\,\,\,\,m(0) = 0,\,\,\,\,p(1) = 9.9013\,\, \times \,\,{{10}^{{ - 5}}}.$$

(2)

The system of equations contains the equation of state of matter ρ = ρ(R), which is unknown for Venus. For the basic density distribution in the Venus model, we take the equation of state from the Earth model PREM. The resulting density profile must satisfy the dimensionless moment of inertia of the planet I/M₀R².

We consider the density of the crust to be constant and equal to 2800 kg/m³. Similar to (Gudkova, Zharkov, 2020), the density in the mantle as a function of pressure ρ_m(p) is given by introducing the coefficient A: ρ_m(p) = Aρ_m0(p), where ρ_m0(p) is the equation of state according to the model of the internal structure of the Earth PREM.

The composition of the core of Venus, as well as the composition of the mantle, may not coincide with the composition of the Earth’s core. To change the core density, the coefficient B is introduced: ρ_c(p) = Bρ_c0(p), where ρ_c(p) is the density in the core of Venus, ρ_c0(p) is the equation of state of the core for the Earth model PREM. The variable parameters of the problem are the core radius, crust thickness, and coefficients A and B. Coefficient A is chosen so that the model mass coincides with the observed one. The model of the internal structure is controlled by the value of the dimensionless moment of inertia I/M₀R². The only experimental value of the moment of inertia is 0.337 ± 0.024 (Margot et al., 2021) has a rather high measurement error, which does not allow imposing strong restrictions on the model of the internal structure of the planet. Another quantity that allows you to control the distribution of density and elastic parameters in the interior of the planet is the tidal Love number k₂.

The system for calculating tidal Love numbers, often referred to as the “system y_in,” is a set of six first-order equations with boundary conditions on the planet’s surface and at the core–mantle boundary (in the case of a liquid core) or in the center (in the case of a solid core) (Alterman et al., 1959; Molodensky, 2001). Usually, the system is reduced to dimensionless variables and solved by the fourth-order Runge–Kutta method (see, for example, Michel and Boy, 2022).

Seventy-two elastic models of the internal structure of Venus have been constructed for crustal values in the range of 30–70 km and core radius in the range of 2800–3500 km. The models are divided into three groups according to the parameter B (B = 1, the equation of state of the nucleus coincides with that of the Earth; B = 1.01, the material in the core of Venus is 1% heavier than in the Earth; B = 0.99, the substance in the core of Venus is 1% lighter than in the Earth). We introduce the following notation for models of the internal structure of Venus depending on the given parameters: crustal thickness in km, parameter B, core radius in km. For example, the model (50, 0.99, 3200) is a model with a crustal thickness of 50 km, B = 0.99 and a core radius of 3200 km.

The simulation results, without taking into account the inelasticity of the interior of Venus, are shown in Figs. 1–4. The following regularities can be traced in the models: (1) in models with a small core (2800–2900 km), the mantle is noticeably heavier than the Earth’s, and in models with a large core (3400–3500 km), it is noticeably lighter; (2) with an increase in the radius of the core, the pressure and density in the center of the planet increase; (3) with an increase in the radius of the core, the moment of inertia of the planet decreases; (4) in models with a thick crust (70 km), the mantle is slightly heavier, and the moment of inertia is somewhat smaller than in models with a thin crust (30 km); (5) when increasing the parameter B, parameter A and the moment of inertia decrease, and the pressure at the center of the planet increases.

Fig. 1.

Model values of physical parameters in the center of Venus depending on the core radius R_c for parameter range B = 0.99, 1.0, 1.0: pressure p_c (a), density ρ_c (b).

Fig. 2.

Model values of the dimensionless moment of inertia I/M₀R² depending on the core radius R_c for parameter range B = 0.99, 1.0, 1.01. The dotted lines show the range of admissible values of the dimensionless moment of inertia.

Fig. 3.

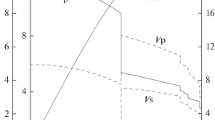
Distributions of physical parameters as a function of radius for the Venus model (30, 1.01, 3100) (crustal thickness 30 km, parameter B = 1.01; the matter in the core of Venus is 1% heavier than in the Earth, the radius of the core is 3100 km): density ρ and gravitational acceleration g (a), pressure p and relative mass m (b), and the velocities of longitudinal and transverse waves V_P and V_S (c).

Fig. 4.

Model elastic Love numbers depending on the core radius R_c for a number of Venus models with the parameter B = 0.99, 1.0 and 1.01: k₂ (a) and h₂ (b). The horizontal dashed lines show the band of valid observations of Love number values k₂.

Figure 1 shows the dependence of pressure p_c and density ρ_c in the center of the planet from the radius of the core, the parameter B and crust thickness. Model pressure values (Fig. 1a) are in the range of 260–310 GPa. For comparison: in the center of the Earth, the pressure reaches 363 GPa, and at the boundary of the inner core, it reaches 328 GPa (Dziewonski and Anderson, 1981). This suggests that even in models with a very large core, the pressure in the center of Venus does not reach the values at which the melt crystallizes under terrestrial conditions. Therefore, the presence of a solid inner core is unlikely, given the same composition and temperature distribution in the interiors of the Earth and Venus. In (Dumoulin et al., 2017), models of Venus with an internal solid core were constructed, using the experimentally obtained equation of state for pure iron, which can crystallize under the conditions of the Venusian interior. However, it is difficult to imagine that there are no impurities of light elements in the core of Venus, which, in turn, reduce the melting point, so we can conclude that, most likely, Venus does not have a solid inner core. It can be seen that the density in the center of the planet (Fig. 1b) increases with increasing core radius and coefficient B. Ratio ρ_c for models with B = 1.01 to ρ_c for models with B = 1.0 turned out to be greater than 1.01, which is due to the fact that with increasing B the pressure in the core increases, which leads to additional compression of the material.

Figure 2 shows the values of the dimensionless moment of inertia depending on the core radius, the parameter B and crust thickness. The dotted lines highlight the range of admissible values of the dimensionless moment of inertia: 0.337 ± 0.024 (Margot et al., 2021). It can be seen that all models fall within the allowable region with a margin, but the closest to the central value of 0.337 are models with a core radius of 3000–3200 km, and models with a core radius of 3300 km and B = 0.99 (large but “light” core). For the model (30, 1.01, 3100) the moment of inertia is exactly 0.337. For this model, Fig. 3 shows the distribution of density, P- and S-wave velocities, gravitational acceleration, mass, and pressure as a function of radius. Due to the fact that the error in measuring the moment of inertia of Venus is quite large, any of the models calculated above cannot be discarded. It was noted above that another criterion is the comparison of the model values of the tidal Love number k₂ with a value derived from observations. Despite the rather high error, the value of the Love number allows us to impose some restrictions on models of the internal structure of Venus.

Figure 4 shows the dependence of the values of the elastic Love numbers k₂ (Fig. 4a) and h₂ (Fig. 4b) on the radius of the core of Venus for the range of parameter B. There is a strong dependence of the number h₂ on the radius of the core, while the thickness of the crust and the parameter B have little effect on the result. Dashed lines in Fig. 4a allocate the range of acceptable values of the Love number k₂. Models with a small core (2800–3000 km) are outside the region of acceptable k₂ values (Fig. 4a) and can be excluded, while models with a core radius of 3300–3500 km are closest to the central value of k₂. This result does not agree well with the values that were chosen when selecting models for the moment of inertia.

When solving the system “y_in” to calculate the tidal Love numbers, it was сonsidered that the planet is a perfectly elastic body, which does not correspond to reality. It was shown in (Zharkov, 2012; Dumoulin et al., 2017; Gudkova and Zharkov, 2020) that the subsurface inelasticity must be taken into account when calculating tidal Love numbers. The models of the internal structure of Venus built above are elastic, and in a dissipative medium, which is the interior of Venus, the shear modulus μ and the tidal Love number of the planet k₂ are functions of frequency. Without regard to rheology, the model values obtained of the Love number k₂ are underestimated. In order to use k₂ as a constraint when building models of the internal structure of Venus, below, when calculating the model tidal Love numbers, the inelasticity of the planet will be taken into account.

Influence of Viscoelasticity

It is known that the damping of mechanical vibrations of the Earth’s interior occurs due to the deviation of the material from ideal elasticity with respect to shear stresses, and the dissipation of mechanical energy is associated precisely with the relaxation of the shear modulus μ (Zharkov, 2013). The distribution of the shear modulus in the interior of the Earth depends on the frequency, i.e., μ = μ(r, ω) and taking into account the frequency dependence leads to a noticeable decrease in the shear modulus during the transition from seismic periods of ~1s to periods of ∼10 min. The frequency of the solar tidal wave on Venus corresponds to a period equal to ~58.4 days (≈5 × 10⁶ s). The Love numbers are approximately inversely proportional to the shear modulus, therefore, their values should increase when moving from an elastic model to an inelastic one.

Above, to calculate the Love numbers, the distributions of the elastic moduli in the PREM model for a period of 1 s (Dziewonski and Anderson, 1981) were used, i.e., the “elastic shear modulus” was used in the calculations. To take into account inelasticity, it is necessary to choose an appropriate rheological model for the behavior of the mantle matter.

To describe the viscoelastic behavior of the Earth’s crust, Maxwell’s rheology is usually used, which gives good results in the study of postglacial uplifts. Maxwell’s rheological body can be represented as a series connection of Hooke’s elastic body with Newton’s linearly viscous body. For short periods, the material described by the Maxwell model behaves like a solid body, while for long periods (in slow processes, the characteristic time of which is much longer than the Maxwell time, which is the ratio of the viscosity coefficient to the elastic shear modulus), as a viscous body. The shear modulus, in turn, varies from the high-frequency value μ(∞) to the low-frequency static value μ(0). In Maxwell’s rheology, the shear modulus and the Lamé parameter λ become complex quantities, and depend on the frequency of external action ω and on the viscosity of the medium η according to the formulas (Peltier, 1974):

$$\tilde {\hat {\mu }} = \frac{\mu }{{1 - i\frac{\mu }{{\omega \eta }}}},\,\,\,\,\tilde {\lambda } = K - \frac{2}{3}\tilde {\mu }.$$

(3)

Maxwell’s rheology was used to take into account the inelasticity in the interior of Venus in (Xiao et al., 2020), in which it was found that the tidal Love numbers deviate significantly from their elastic value only at values of viscosity in the mantle less than 10¹⁸ Pa s. The application of Maxwell’s rheology for the models of the internal structure of Venus calculated above gave similar results. This means that even if the viscosity in the Venusian mantle is an order of magnitude less than the viscosity in the Earth’s mantle, the effect of inelasticity on the Love numbers is negligible. However, it was shown in works (Dumoulin et al., 2017; Gudkova and Zharkov, 2020) that k₂ increases noticeably when moving from an elastic model to an inelastic one. The reason for the discrepancy between the results is the use of different rheological models.

Maxwell’s rheology turns out to be less suitable for seismic and tidal periods. Experimental results (see, e.g., Gribb and Cooper, 1998; Jackson and Faul, 2010; Jackson, 2015) show that Maxwell’s rheology poorly describes the behavior of olivines and other minerals present both in the Earth’s mantle and in other bodies of the Solar System. To describe the behavior of planetary bodies, more complex rheologies are proposed, such as Andrade’s rheology, which is now actively used in many studies of planets and satellites, especially when tidal interactions are considered (Castillo-Rogez et al., 2011; Bierson and Nimmo, 2016; Dumoulin et al., 2017; Renaud and Henning, 2018; Bagheri et al., 2022). The authors of these papers came to the conclusion that Andrade’s rheology describes the behavior of mantle matter in planets much better than Maxwell’s rheology. Therefore, below, we will use the Andrade rheology to take into account the inelasticity in the interior of Venus.

In describing Andrade’s viscoelastic rheology, the complex shear modulus $\tilde {\hat {\mu }}$ equals ${1 \mathord{\left/ {\vphantom {1 {\tilde {\hat {J}}}}} \right. \kern-0em} {\tilde {\hat {J}}}}$, where $\tilde {\hat {J}}$ is called the “complex compliance” and is given by the formula (Castillo-Rogez et al., 2011)

$$\tilde {\hat {J}}(\chi ) = J\left[ {1 + {{{(i{{\tau }_{{\text{M}}}}\chi )}}^{{ - \alpha }}}\Gamma {\text{(1}} + \alpha {\text{)}}} \right] - \frac{i}{{\eta \chi }},$$

(4)

$J = {1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0em} \mu },$ ${{\tau }_{{\text{M}}}} = {\eta \mathord{\left/ {\vphantom {\eta \mu }} \right. \kern-0em} \mu }$ is the Maxwell time, χ is the tide frequency, Γ is the gamma function, and α the Andrade parameter.

The Andrade parameter α lies in the range 0.2–0.5 (Gribb and Cooper, 1998; Castillo-Rogez et al., 2011; Dumoulin et al., 2017), although α ≈ 0.3. Below, we take the values α = 0.2 and α = 0.5 as limiting cases, thus covering the range of possible values of k₂ and h₂ for each model.

Based on the analysis of the distribution of viscosity in the interior of the Earth, when calculating the Love numbers k₂ and h₂ for models with Andrade rheology, we will take two test distributions of viscosity in the interior of Venus:

(1) Low-viscosity distribution:

– Viscosity of the crust 10²¹ Pa s.

– Viscosity of the upper mantle 10¹⁹ Pa s.

– Viscosity of the lower mantle 10²¹ Pa s.

(2) High-viscosity distribution:

– Viscosity of the crust 10²³ Pa s.

– Viscosity of the upper mantle 10²¹ Pa s.

– Viscosity of the lower mantle 10²³ Pa s.

The viscosity of the core is assumed to be zero.

The crust thickness and parameter B have little effect on the Love numbers compared to the radius of the nucleus, so the Love numbers k₂ and h₂ taking into account viscoelasticity will be calculated only for models with a crust thickness of 30 km and the parameter B = 1.0 (30, 1.00, 2800–3500) for two cases of viscosity distribution in the interior of Venus (the case of high and low viscosity), and for two values of the parameter α: α = 0.2 and α = 0.5. This is justified by the fact that the uncertainty in the distribution of viscosity and parameter α affects the result more strongly than the thickness of the crust and the coefficient B.

The ranges of viscosity and parameter α lead to a large spread of possible values of the Love numbers for each test model of the internal structure. At α = 0.5, k₂ and h₂, taking into account the inelasticity, are only 0.2–3% higher than the elastic values. At α = 0.2, the difference is 5%–17% for the considered viscosity profiles. If the viscosity in the lower mantle of Venus is less than 10²¹ Pa s, then the Love numbers, taking into account the inelasticity, are 20% higher than the values for the elastic model.

Values of the real part of Love numbers k₂ and h₂ for models (30, 1.00, 2800–3500), taking into account viscoelasticity, depending on the core radius, are shown in Fig. 5. Models with a small core (2800–2900 km) fall within the observation data interval for k₂ (0.229–0.361) only at low viscosity and parameter α close to 0.2, but even so, they are on the edge of the acceptable range, and therefore these models can be considered less likely. To select the optimal model, more accurate measurement of k₂ and a better understanding of which value of the parameter α is more consistent with the behavior of mantle matter are required. Nevertheless, Fig. 5a shows that if the viscosity is low, then models with a core radius of 3100–3400 km are preferable, and if the viscosity is high, then with a core of 3200–3500 km. Since the viscosity decreases exponentially with increasing temperature, the large core indicates a “cold mantle,” while the middle core indicates a “hot mantle.”

Fig. 5.

Model values of the real part of inelastic Love numbers depending on the core radius R_c for a number of Venus models with the parameter B = 0.99, 1.0 and 1.01: Re(k₂) (a) and Re(h₂) (b). The horizontal dashed lines show the band of valid observations of Love number values k₂.

Consider jointly the restrictions on the calculated models of the internal structure of Venus in terms of the Love number k₂ and moment of inertia I/M₀R² (Fig. 6). Let us determine the probability of the model with a Love number k₂ and moment of inertia I/M₀R² as

$$p = \exp \left( { - \frac{{{{{({{k}_{2}} - {{\mu }_{1}})}}^{2}}}}{{2\sigma _{1}^{2}}} - \frac{{{{{\left( {\frac{I}{{{{M}_{0}}{{R}^{2}}}} - {{\mu }_{2}}} \right)}}^{2}}}}{{2\sigma _{2}^{2}}}} \right),$$

(5)

where μ₁ = 0.295, σ₁ = 0.033, μ₂ = 0.337, σ₂ = 0.024. According to (Konopliv and Yoder, 1996) the range of allowable values of k₂ = 0.295 ± 0.066 corresponds to an error of 2σ, therefore σ₁ = 0.033.

Fig. 6.

Dimensionless moment of inertia I/M₀R² and the Love number k₂ (for elastic models and inelastic models with high and low viscosity). Dotted lines mark I/M₀R² = 0.337 and k₂ = 0.295. The solid lines show the probability of the models.

The solid lines in Fig. 6 show the probability of the models. From Fig. 6, the following conclusions can be drawn: if the viscosity of the Venusian mantle is high, then models with a core radius in the range of 3200–3500 km are more probable; if the viscosity of the Venusian mantle is low, then models with a core radius in the range of 3100–3400 km are more probable.

As noted above, the Love number h₂ characterizes the radial displacement of the surface due to tidal action. If a planet with mass m₁ and radius R is affected by the tidal potential W from the side of a body with the mass m₂ located at a distance d from the planet, then the second harmonic W₂ of the tidal potential W in the expansion in Legendre polynomials is calculated using the formula

$$\begin{gathered} {{W}_{2}}(\varphi ) = - \frac{{G{{m}_{1}}}}{R}\frac{{{{m}_{2}}}}{{{{m}_{1}}}}{{\left( {\frac{R}{d}} \right)}^{3}}{{P}_{2}}(\cos \varphi ) \\ = {{V}_{0}}\frac{{{{m}_{2}}}}{{{{m}_{1}}}}{{\left( {\frac{R}{d}} \right)}^{3}}{{P}_{2}}\cos (\varphi ), \\ \end{gathered} $$

(6)

Where G is the gravitational constant, φ is the latitude, and V₀ is the gravitational potential on the unperturbed surface.

The maximum radial displacement u_max of the surface is then

$${{u}_{{\max }}} = \frac{3}{2}{{h}_{2}}R\frac{{{{m}_{2}}}}{{{{m}_{1}}}}{{\left( {\frac{R}{d}} \right)}^{3}}.$$

(7)

In Fig. 5b, for model Love numbers h₂, taking into account inelasticity, the corresponding radial displacement of the surface of Venus due to tidal action is given by u_max in centimeters. Values of h₂ are in the range 0.4–0.75, which corresponds to a radial displacement of the surface by 25–50 cm. According to (Cascioli et al., 2021), the VERITAS mission plans to measure the radial displacement of the surface of Venus with an accuracy of ~10 cm. This is a small accuracy, but the measurement of h₂ with such accuracy will be able to impose a restriction on the distribution of parameters in the interior of Venus.

Tidal Phase Shift

Due to the inelasticity of the planet’s interior, the deformation of its figure during tidal interaction lags behind or advances by some angle the line connecting the centers of two bodies: the planet and the body that causes tidal action. The angle of lag of the tidal bulge (or phase shift) in radians is defined as

$$\varepsilon \approx {1 \mathord{\left/ {\vphantom {1 {2Q}}} \right. \kern-0em} {2Q}} = \frac{{\operatorname{Im} ({{k}_{2}})}}{{2\left| {{{k}_{2}}} \right|}}\,\,\,\,{\text{or}}\,\,\,\,\varepsilon \approx \frac{{\operatorname{Im} ({{h}_{2}})}}{{2\left| {{{h}_{2}}} \right|}},$$

(8)

where Q is the quality factor of the planet.

Thus, the value of the retardation angle of the tidal hump can be used to determine the viscosity of the planet: the higher the retardation angle, the less viscous the material, the higher the Love number and the greater the deformation. The model values of the delay angle for the considered models are shown in Fig. 7. The two sets of models differ in viscosity by two orders of magnitude and can be distinguished by measuring the lag angle. The difference between the lag angles for k₂ and h₂ is small compared to the scatter caused by the uncertainty of the Andrade parameter α. The lag angle for high viscosity models is about half that of low-viscosity models. There is a tendency for the delay angle to decrease when moving from models with a small core to models with a large core.

Fig. 7.

Angle of lag of the tidal bulge (phase shift) ε in degrees for models of the internal structure of Venus with high and low viscosity depending on the radius of the core R_c.

According to (Rosenblatt et al., 2021; Cascioli et al., 2021), in the EnVision and VERITAS missions in the late 20s and early 30s, the lag angle will be measured to within ~0.1°. This will help determine the average viscosity of Venus’s mantle to within an order of magnitude. If the phase shift is higher than 0.9°, then the viscosity of the mantle is low, and if it turns out to be below 0.4°, the viscosity is high.

CONCLUSIONS

The wide range of acceptable values of k₂, the uncertainty of the moment of inertia, and the lack of measurements of the dissipative factor lead to the fact that at present it is impossible to accurately determine the radius of the core, the composition of the mantle, and the temperature profile of Venus. In this paper, on the basis of Earth’s PREM model, 72 models of the internal structure of Venus are constructed, in which the crustal thickness varies from 30 to 70 km, and the core radius from 2800 to 3500 km. The cases of low, medium and high density of matter in the mantle and core are considered in comparison with the composition of the basic model. For the model (30, 1.01, 3100), the profiles of pressure, density, seismic wave velocities, elastic moduli, and gravitational acceleration are given. An analysis of the results obtained and their comparison with experimental data made it possible to draw some conclusions about the mantle and core of Venus.

The pressure in the center of the planet is much less (by tens of GPa) than the pressure at the boundary of the Earth’s inner core. One of the important conclusions is that the presence of a solid inner core for Venus is unlikely and is possible only if the core of Venus contains significantly fewer light elements compared to the core of the Earth.

Unfortunately, the measurement accuracy of the moment of inertia is 0.337 ± 0.024 (Margot et al., 2021) is not yet high enough to impose strong restrictions on the model of the internal structure of Venus. For all calculated models, the values of the moment of inertia lie in the range from 0.323 to 0.347, which is consistent with the measured value. It is shown that, without taking into account the inelasticity of the interior, underestimated model values of the tidal Love number k₂ are obtained. To describe the inelasticity of the interior of Venus, the Andrade rheological model was adopted. In this case, the Love numbers become complex quantities and their values increase in comparison with the elastic values. In models with high viscosity of the mantle material, this difference is more than 7%, and in models with low viscosity, 17%. Ideas about the structure of Venus strongly depend on which of the considered cases occurs.

Joint analysis of the model values of the moment of inertia and the viscoelastic Love number k₂ allows us to draw the following conclusions: models of Venus with a core radius less than 3000 km are unlikely; if the viscosity of the mantle is high, then the radius of the core lies in the range of 3200–3500 km; if the viscosity of the mantle is low, then the radius of the core is 3100–3400 km.

Due to the large error in the measurements of the moment of inertia and the Love number k₂ it is not yet possible to make a choice between models with a core radius of 3100 and 3500 km. Also, an obstacle in the refinement of the radius is the uncertainty of the Andrade parameter α in the rheological model of the interior’s behavior.

The angle of retardation of the tidal bulge is calculated for the constructed models. Its value has not yet been measured, but if it turns out to be higher than 0.9°, then we can confidently speak of a fairly low viscosity of the mantle of Venus (compared to the Earth); if below 0.4°, the viscosity of the mantle is high. The viscosity estimate, in turn, provides valuable information about the temperature distribution in the interior of Venus.

The creators of the spacecraft VERITAS and EnVision promise to provide very accurate measurements of the moment of inertia (1.4%), the Love number (0.3%) and the angle of retardation of the tidal bulge (0.1°) (Cascioli et al., 2021; Rosenblatt et al., 2021), with which it will be possible to make fairly accurate estimates of the core radius and the average viscosity of the mantle. This will help to fully characterize the internal structure of Venus and, thereby, learn more about the evolution of Earth’s “twin.”