INTRODUCTION

Fullerenes, which have unique chemical and physical properties, have drawn the attention of many researchers since their discovery in 1985, due to their wide use in industry [1]. They are, however, incompatible with water and aqueous solutions [2–5], which considerably limits their use. The solubility of C60 in water is only 0.02 ng/L [2], which is also observed for most derivatives of lower fullerenes (fluoro-, chloro-, bromo-, iodo-, oxo-, amino-, and carboxyl). These are usually very poorly soluble in water and solutions [5–7]. At the same time, water-soluble fullerene derivatives are widely used in mechanical engineering, construction, medicine, pharmacology (due to their good compatibility with water, physiological solutions, blood, lymph, and gastric juice), cosmetology (in aqueous and water–alcohol solutions), science, and technology. Among the many ways in which they have been studied in these fields, the preparation of stable aqueous fullerene dispersions [8, 9] (the size of fullerene clusters depends on the procedure and varies in the nanometer range) and stable complex associates with hydrophilic substances [3, 4, 10–12] are worthy of note. In both cases, the stability of systems depends strongly on their environment. In addition, such products are not individual substances, so their use as initial reagents to obtain different water-soluble fullerene adducts is unacceptable [13]. The third way of fullerene functionalization is to add hydrophilic groups to a fullerene core (i.e., prepare adducts). This technique is the one most versatile, due to the weakly conjugated double bonds in fullerenes and their high tendency to react at double bonds (nucleophilic and radical addition reactions). Most of the adducts formed by these ways are fairly stable, allowing the use of further chemical modifications to obtain new biologically active substances [13]. The most common reactions in fullerene chemistry are cycloaddition, which are known in organic chemistry as Diels–Alder diene synthesis, where C60 always participates as a dienophile [3, 14]. Reactions of the one-stage addition of primary and secondary amines, and direct addition of amino acids and dipeptides to fullerene, proceed according to a radical mechanism [15, 16]. The resulting compounds are stable and physiological, since natural amino acids are used in their synthesis. This was confirmed by biological tests in the late 1990s and after [17–19]. From the biological and chemical points of view, one of the most important problems in using fullerenes is therefore preparing water-soluble fullerene compounds and derivatives of them that are based on different amino acid matrices. The present work is devoted to this problem.

SYNTHESIS AND IDENTIFICATION OF ADDUCTS OF LOWER FULLERENES WITH AMINO ACIDS

Different classes of water-soluble fullerene derivatives have so far been synthesized. These include fullerenols and their esters with carboxylic and dicarboxylic acids, with amino acids, and with peptides and proteins [15–53]. Along with several C60 monofunctional derivatives containing polar side chains, polyamino and polyhydroxyl fullerenes were studied as in early as in the first half of the 1990s [27, 28]. A large number of polyhydroxylated fullerene derivatives, tested in different chemical and biological model systems and displaying both antioxidant and prooxidative properties, were described in [53]. Several mechanisms were proposed for the antioxidant activity of fullerenols, and patents relating to antioxidant properties of fullerenol were filed. The first work by Hirsch et al. on fullerenes containing multiple covalently bound substituents of an amine derivative appeared in 1991 [15]. All derivatives displayed high solubility in water [15–30]. The authors showed that the higher the number of water-soluble groups added to fullerene, the stronger its water solubility. The main problem in synthesizing water-soluble fullerene adducts with hydrophilic compounds (amino acids and peptides) is the incompatible solubility of reaction components (very hydrophobic fullerenes and hydrophilic amino acids). Aprotic non-polar environments are needed to dissolve fullerenes, while polar aqueous ones are required for amino acids. The heterogeneity of a reaction system prolongs the reaction time and lowers the yield of the target product. If heating is used, it can racemize an added addend (e.g., an amino acid or peptide) [13].

A way of synthesizing a functionalized fullerene with symmetric polar organic fragments and 1 to 20 carbon atoms with optional oxygen or nitrogen was patented in the United States in 2001 [54]. It should, however, be considered purely preparative, due to its complexity and multistage nature. The preparation of amino acid adducts (lysine derivative) by synthesizing a aminocaproic acid fullerene derivative and subsequently adding it to a lysine derivative of a glycopeptide was first patented in [55]. Salts of aminocaproic and aminobutyric acids with alkali metals were used in reactions with fullerene as 18-crown-6 complexes. The system was heterogeneous: o-dichlorobenzene and water heated at 60°С for 6–8 h. The solvents were then distilled off, and the residue was treated with a saturated solution of potassium chloride and water.

Many fullerene derivatives with amino acids have been studied theoretically. The ability of C60 fullerene to interact with amino acids was studied at the theoretical level in [56]. Calculations performed at the DFT-B3LYP/3-21G level of theory showed that the best interactions were between fullerene and arginine, leucine, and tryptophan, due to the framework structure of these amino acids. The molecular structures of C60 hybrid amino acid derivatives were determined via quantum-chemical calculations [57]. Calculations used to study amino acid fullerenes derivatives at the atomic and molecular levels are described more thoroughly below.

Both C60 and C70 fullerenes functionalized with amino acids were synthesized and studied in subsequent years to identify them and determine their purity and physicochemical properties [58–81]. Some works described the biological activity of water-soluble amino acid fullerene derivatives [9, 29, 82–86].

Fullerene C60 amphiphilic derivatives with alanine, cysteine, and arginine were synthesized and characterized in [45]. The authors concluded that fullerene C60 derivatives with amino acids can prevent oxidative stress-induced cell death without obvious toxicity. A fullerene C60 derivative with lysine was synthesized and its biological activity was studied in [50]. The authors of [51] synthesized a glycine fullerene C60 derivative. Studies of the cytotoxicity of this derivative on lines of cancer cells showed that kills them. The neuroprotective properties of hybrid structures based on C60 and proline derivatives were studied in [18, 78]. The authors found that each compound had antioxidant activity and suppressed the glutamate-induced adsorption of Ca2+ ions in the synaptosomes of a rat’s cerebral cortex.

Most works describe C60 fullerenes. Much fewer deal with the synthesis of derivatives of C70 fullerene. Their biological action and physicochemical properties can differ considerably, despite their apparent similarity [80, 81].

It should be noted that a great many works provide no means of synthesis or identifying data for derivatives. They also describe few physicochemical properties of fullerene derivatives, despite their importance in optimizing and developing the most promising practical uses of carbon nanoclusters. Ways of synthesizing fullerene derivatives are also mostly preparative and allow the production of only milligram quantities, while data on the biological activity of fullerene derivatives are not compared and no relationships between them and physicochemical properties are revealed [87].

Figure 1 shows the structural formulas of some C60 amino acid adducts. Table 1 shows schemes for synthesizing various amino acid fullerene adducts with specific stoichiometric compositions and ways of identifying them. These include IR spectroscopy, Raman spectra, electron spectroscopy, nuclear magnetic resonance, high performance liquid chromatography, liquid chromatography–mass spectrometry, elemental analysis, and (less often) and thermal analysis with mass spectrometry. Figures 2–6 and Table 2 show some ways of identifying adducts [87].

Fig. 1.
figure 1

Structural formulas of some C60 amino acid adducts.

Full size image
Table 1.    Synthesis and identification of lower fullerene (C60) amino acid adducts
Full size table
Fig. 2.
figure 2

Image of crystals of L-lysine C60 derivative (С60(C6H14N2O2)2).

Full size image
Fig. 3.
figure 3

IR spectrum of L-hydroxyproline C60 derivative (С60(C5H9NO3)2).

Full size image
Fig. 4.
figure 4

Electronic spectrum of L-arginine C60 derivative (C60(C6H13N4O2)8H8); D is the optical density; and λ is the wavelength.

Full size image
Fig. 5.
figure 5

Liquid chromatogram of L-threonine C60 derivative (С60(C4H9NO3)2). Conditions: Phenomenex® NH2 column (150 × 2.0 mm, 5 μm, 100 A); acetonitrile/aqueous solution of acetic acid (0.1%) (5 : 95) as the eluent at 0.2 mL/min; sample volume, 20 μL; diode matrix.

Full size image
Fig. 6.
figure 6

Thermal analysis of a crystalline hydrate of L-lysine C60 derivative (С60(C6H14N2O2)2).

Full size image
Table 2.   Complex thermal analysis of L-lysine C60 derivative (С60(C6H14N2O2)2)
Full size table

COMPUTER MODELING OF THE PHYSICOCHEMICAL PROPERTIES OF AMINO ACID FULLERENE DERIVATIVES

The main theoretical ways of studying amino acid fullerene derivatives and calculating their physicochemical properties are density functional theory (DFT) and molecular dynamics. Application of DFT is based on the relationship between the properties of molecules and their electronic structure. Properties of simulated systems in molecular dynamics are determined mainly by intermolecular interactions which indirectly (through force fields), also depend on the electronic structure.

Heat capacity was first calculated for a fullerene derivative with amino acid C60–Arg in [65] using a wide range of temperatures. The calculations were performed in a DFT harmonic approximation using the DMol3 module of Materials Studio software. C60–Arg geometry was optimized with PBE, PW91, and HCTH functionals using the DNP (4.4) full electronic atomic basis and convergence of the total energy equal 2 × 10−5 Hartree.

Heat capacity was calculated for two types of C60–Arg molecules with different arrangements of amino acid residues with uniform (Fig. 7a) and “Saturn-like” distributions (Fig. 7b) at temperatures of 50 to 320 K. Results showed there was a good agreement between the calculated and experimental data at ~50 K. The systemic error grew along with temperature and was 20% at 320 K, due to a substantial contribution from anharmonicity at high temperatures. Different isomers did not affect the heat capacity.

Fig. 7.
figure 7

C60–Arg fullerene derivative with (a) uniform and (b) “Saturn-like” arrangements of amino acid residues.

Full size image

The electronic structure of a C70 and L-threonine derivative (C70–Thr) was calculated via DFT implemented in the DMol3 module (Materials Studio software) at the PW91 level of theory, in combination with a DNP basis (4.4) in the full electronic approach [88]. The charges of atoms were determined according to Mulliken’s scheme after complete optimization of the geometry of molecules. The dynamic and the structural properties of C70, Thr, and C70–Thr were found by conventional molecular dynamics using a Forcite module with UFF force field and atomic charges calculated at the previous stage. Modeling took 500 ps. C70–H2O and C70–Thr–H2O binary systems were modeled using 1500 water molecules per fullerene molecule and fullerene derivative. A binary system containing L-threonine was modeled using two Thr molecules and the same number of water molecules. These binary systems were studied using the NVT ensemble with MD modeling at T = 293.15 K and a Nose thermostat.

Figure 8 shows the electron density distributions for C70, Thr, and C70–Thr molecules, calculated with DFT. Table 3 shows the calculated atomic charges for Thr and C70–Thr molecules. The main features of the obtained results are associated with nitrogen atomic charges in amino acid and in fullerene derivative. The electronic system of fullerene probably attracted the electron pairs of nitrogen atoms and reduced all atomic charges in the amino acids. Figure 9 shows the radial distribution function (RDF) between water molecules and nitrogen atoms from amino acid (Thr) and the C70–Thr derivative. It is clear that both nitrogen atoms in the fullerene derivatives are shielded by fullerene core and amino acid residues, while individual amino acids are more accessible to water molecules. Figure 9 shows the RDF between carbon atoms of a fullerene core and water molecules. The functionalization of fullerene with two L-threonine groups is insufficient for any appreciable change in the distribution of water molecules around the fullerene core. Figure 10 shows the RDFs between water molecules and oxygen atoms of hydroxyl, carboxyl, and carbonyl groups. Analysis of the results indicates that the closest proximity of water molecules is observed for the oxygen atoms in the carbonyl group.

Fig. 8.
figure 8

Distribution of electron density in (a) fullerene C70, (b) threonine, and (c) C70–Thr derivative.

Full size image
Table 3.   Average charges (in electron charge units) of nitrogen and oxygen atoms of hydroxyl (–OH), carboxyl (‒COOH), and carbonyl (C=O) groups, determined according to Mulliken’s scheme
Full size table
Fig. 9.
figure 9

Radial distribution functions between water molecules and nitrogen atoms in (a) C70–Thr and (b) threonine molecules.

Full size image
Fig. 10.
figure 10

Radial distribution functions between water molecules and oxygen atoms of: (1) hydroxyl, (2) carboxyl, and (3) carbonyl groups.

Full size image

The shielding values for all carbon atoms of the C60–Arg molecule were calculated with DFT using the plane wave basis set in the CASTEP program to explain NMR spectra [89]. The calculations were performed with a PBE functional using a set of plane waves with cutoff value of 610 eV. The 13C NMR spectra were calculated relative to tetramethylsilane. A comparison of the experimental and calculated spectra shows that the isomer with a “Saturn-like” (Fig. 7b) distribution of amino acid residues better describes the experimental spectrum (Fig. 11), as was confirmed by calculating the total energy of the isomers. The difference between the total energies of the “Saturn-like” isomer and the one with a uniform distribution of amino acid residues was 6.5 eV (i.e., the “Saturn-like” isomer was more stable).

Fig. 11.
figure 11

13C NMR experimental spectrum obtained via CP/MAS (contact time, 2 ms) and calculated with DFT.

Full size image

The conventional molecular dynamics employed in the FORCITE program of the Materials Studio software was used to calculate dynamic structure. The COMPASS II force field with appropriate charges was also used. The distributions of amino acid residues over the fullerene core were found to be uniform and “Saturn-like” (Fig. 7b). A cell with periodic boundary conditions containing one C60–Arg derivative molecule and 1500 water molecules was used in calculations. A C60‒Arg–water binary system was calculated at T = 300 K in the NVT ensemble for 1000 ps.

Molecular dynamics calculations showed that the most important property influencing interaction between the C60–Arg derivative and water molecules was a steric factor. Figure 12 shows data of the radial distributions between each type of atom of the C60‒Arg isomers (“Saturn-like” and uniform). We can see that (i) water molecules in the “Saturn-like” structure were closer to fullerene atoms than that in the uniform distribution, (ii) the oxygen atoms of the hydroxyl groups of both isomers attracted water molecules most strongly, and (iii) water molecules were closer to all atoms of the C60–Arg molecule in the “Saturn-like” isomer, due probably to the higher degree of ionicity of the “Saturn-like” isomer.

Fig. 12.
figure 12

Radial distribution function for the oxygen atoms of water and different atoms of C60–Arg derivative: (I) carbon atoms of a fullerene core; (II) nitrogen atoms of arginine residues; (III) oxygen atoms of arginine residues. The upper graphs correspond to uniform distributions of functional groups; the lower ones, to “Saturn-like” distributions; un—unmodified fullerene.

Full size image

An isomer with a polar arrangement of amino acid residues of hydroxyproline C60–Hyp (Fig. 13) was selected, based on the minimum total energy calculated via DFT using the DMol3 program with a PBE functional and DNP atomic basis [90]. The charges were determined according to Mulliken’s scheme. The molecular dynamics implemented in the FORCITE module of the Material Studio software was used to determine the arrangement of water molecules in a C60–Hyp aqueous medium. The modeled system contained one C60–Hyp molecule and 3000 water molecules. An NVT ensemble, 5 ns duration, a 1 fs time step at T = 298.15 K, and a UFF force field with calculated charges were used in calculations. Table 4 gives atomic charges a–f (Fig. 14).

Fig. 13.
figure 13

C60–Hyp isomer with polar arrangement of amino acid residues. Letters a–e correspond to atoms shown in Table 4.

Full size image
Table 4.   Calculated atomic charges (in electron charges) of the C60–Hyp derivative used in calculations with molecular dynamics (a–f, Fig. 13)
Full size table
Fig. 14.
figure 14

Radial distribution functions of different atoms in C60–Hyp: (a) oxygen of the hydroxyl group; (b) carbon atoms of the modified fullerene core; (c) nitrogen atom; (d) oxygen atom of the carbonyl group; (e) oxygen atom of the carboxyl group.

Full size image

Results from computer modeling with molecular dynamics (Fig. 13) showed that water molecules were closest to the oxygen atoms of carboxyl groups (3.25 and 3.21 Å) (Fig. 14, d, e), due to the combined actions of two closely located oxygen atoms; this was not observed for the more charged single oxygen atoms of the hydroxyl groups (3.31 Å) (Fig. 14, a). The maximum RDF value of water molecules relative to the carbon atom of a fullerene core (Fig. 14, b) shows that water molecules come closer to this atom much less than the oxygen atoms of an amino acid residue. Nitrogen atoms (5.55 Å) (Fig. 14, c) have almost no contact with water molecules, due to steric hindrances.

Compounds in which an amino acid is not bound to a fullerene by a chemical bond and a stable complex forms through noncovalent interactions have been studied in some works on the computer modeling of amino acid fullerenes adducts. Only interactions between pristine fullerene and amino acid molecules were analyzed in these works, although fullerene cores modified with different atoms and functional groups were calculated as well.

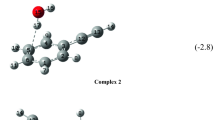
DFT was used in combination with the 6-31G(d) basis set to calculate adsorption complexes of fullerene and phenylalanine in the gas phase and in water at the M062X and B3LYP levels of theory [91]. Kaya et al. showed that the energy of bonds between an amino acid and fullerene at four probable sites of adsorption of a phenylalanine molecule depends on the electron density distribution after complete optimization of the geometry of the complex. The distances between a phenylalanine molecule and a fullerene core (M062X functional) were 3.61 and 3.60 Å in the gas phase and water, respectively, and 4.38 and 4.45 Å for a B3LYP functional.

The interaction between C60 fullerene and an L‑histidine molecule was modeled computationally [92]. RHF/6-31G* was used to calculate the electronic structure and for complete geometry optimization. The energy of interaction between the amino acid molecule and the fullerene core was determined at the MP2 level of theory. The distance between the hydrogen atoms of the amino acid molecule, which have a weakly positive charge, and the atoms of the fullerene molecule were 3.0–3.1 Å.

The noncovalent interaction between 20 L-amino acids and C60 fullerene core was studied via DFT (the DMol3 module of the Materials Studio software) using the PBE functional, DNP basis, and Grimme correction for noncovalent interactions [93]. The geometry of the complexes in the gas phase and water was completely optimized, and the total energy of the system was calculated. The energies of formation of complexes in vacuum and water were analyzed comparatively in this work. The limited nature of the approach, according to which the interaction between amino acid molecule and fullerene core obeys a hydrophobic mechanism, was demonstrated.

Interaction between proline molecules and the surfaces of C60 fullerene cores was studied in [94]. The B3LYP/6-31G(d) approach employed in Spartan was used in calculations. The optimum geometry (bond lengths), IR spectra in the range of 298.15–398.15 K, the energy of adsorption, and the orbital energies of HOMO and LUMO were calculated. It was shown that the adsorption of proline on a fullerene core is endothermic and impossible in actual experiments.

An effective way of calculating the pKa of a L-alanine-C60 adduct by quantum-chemical means was proposed in [95]. HF and DFT (Gaussian software) were used in combination with the 6-31G(d) basis set and B3LYP functional to calculate the equilibrium geometry and vibrational frequencies in the gas phase. The energies of hydration and the electron energies in water were then calculated using the PCM continuum model. The isomers of the adduct were considered in detail, and the one most energetically favorable was found. It was shown that the formation of COO‒–CH(Me)–NH\(_{2}^{ + }\)–C60H and COOH–CH(Me)–NH\(_{2}^{ + }\)–\({\text{C}}_{{60}}^{ - }\) zwitterions with negative charges localized on COO– or \({\text{C}}_{{60}}^{ - }\) was quite impossible.

DFT was used to calculate the energies of interaction between fullerene and peptides from lysine and alanine using the BLYP and VWN functionals in combination with the DNP basis set (the DMol3 module of the Materials Studio package) [96]. The authors showed that the BLYP functional cannot be used to model such systems, while the VWN functional gives reliable and somewhat underestimated values. Molecular mechanics was used, and the AMBER and MM+ force fields (HyperChem package) were studied in [96]. The best results were obtained for the AMBER force field. Such calculations clearly demonstrate the possibilities of using computational means to study the interaction between protein molecules and fullerene.

The adsorption of alanine on fullerene C60 was modeled via DFT [97]. A model complex was optimized using the M062X functional and the 6-31G* basis set (Gaussian program). The energies of adsorption, reactivity indices, atomic charges, and global electron density transfer (GEDT) in the gaseous and aqueous phases were calculated. It was shown that a stable compound formed at distances of 3.03–3.07 Å between an alanine molecule and a fullerene core.

The noncovalent interactions of glycine encapsulated into a C60 fullerene were studied in [98]. The M06-2X functional and 6-311G(d,p) basis set were used. Results from calculations showed that the fullerene core strongly affects the structure and the electronic properties of a glycine molecule inside it. The amino acid molecule is deformed and tends to form a zwitterion, despite strong repulsion from fullerene carbon atoms, and the spatial arrangement of a glycine molecule is due to the interaction between nitrogen atoms and the fullerene’s electronic system.

The energies of hydration of aspartic acid and methionine fullerene adducts were calculated in [99]. Products consisting of a fullerene core and five homogeneous amino acid residues were considered. The energy of hydration was calculated via DFT using both the UA and PCM approaches to the continuous monitoring of the medium and a generalized Born procedure. The charges on atoms were found according to Mulliken’s scheme following calculations at the B3LYP level of theory, in combination with the 6‑31G(d) and 6-31+G(d,p) basis sets. The energy of hydration for neutral and charged fullerene C60 amino acid adducts was reproduced quite well using the generalized Born procedure.

The adsorption of aminolevulinic acid with fullerene C60 was modeled in [100]. DFT calculations were performed using the GAMESS program at the B3LYP level of theory, in combination with the 6-31G* basis set. Calculations showed that electrostatic energy plays an important role in the adsorption of amino acids, while the electronic properties and geometric structure of a fullerene core change negligibly.

Modern computational modeling at the atomic-molecular level thus allows us to better understand both electronic and structural features of amino acid fullerene derivatives and their physicochemical properties.