INTRODUCTION

A huge number of intriguing and exquisite observations have been made with the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). Many of them could have never been systematically studied at the accelerators of previous generation. In particular, hard multiparton interactions (MPI) are just among these interesting phenomena. The existence of MPI in hadron–hadron collisions at high energies is a natural consequence of the steep increase in the parton flux at small parton longitudinal momentum fractions, together with the unitarity requirement for the cross sections in perturbative QCD. The inclusive cross section of a hard process is usually calculated under the assumption that, in any collision, along with many soft interactions, there occurs only a single hard interaction because of its relatively low probability. Nevertheless, it is also possible that two (or more) different parton pairs undergo hard scattering in the same hadronic collision. These double parton scatterings (DPS) have been theoretically studied for many years, starting from the early days of the parton model. The current state of the MPI theory and the results of many years of research have been recently reviewed in a book [1] (see also a review [2]), which contains an extensive bibliography. Thus, the investigation of double, triple, and n-parton scatterings [3, 4] allows us to extract unique and completely new information about the yet unknown three-dimensional partonic structure of hadrons and about momentum, flavor, and color correlations in their wave function.

The DPS events have been initially observed by the AFS (Axial Field Spectrometer) [5] and UA2 (Underground Area 2) [6] collaborations at CERN and later by the CDF (Collider Detector at Fermilab) [7, 8] and D0 [9, 10] collaborations at the Tevatron, with sufficiently high statistics for primary analysis and study. As expected, the LHC luminosity and energy provided the observation [1] of events with hard MPI’s in numbers that are considerably larger than those in the aforementioned experiments. The DPS contribution has now been reliably separated and measured [1] in a number of processes containing in the final state jets, gauge bosons (\(\gamma ,\;W,\;Z\)), heavy quarks (\(c,\;b\)) and quarkonia (\(J{\text{/}}\psi \), \(\Upsilon \)). For example, here is the list of some recent results from the collaborations ATLAS (A Toroidal LHC ApparatuS) [11–13], CMS (Compact Muon Solenoid) [14–16] and LHCb (Large Hadron Collider beauty) [17–19]. A triple parton scattering has also been observed very recently [20], in accordance with an early suggestion [3, 21].

The DPS is actively discussed for proton–nucleus (\(p\)–\(A\)) and nucleus–nucleus (\(A\)–\(A\)) collisions as well, since its relative contribution increases, compared to naive scaling expectation. Unique new options emerge for further studies and measurements of momentum correlations. The latest achievements in and prospects for these studies may be found in a review [4]. For nucleus–nucleus collisions, it opens yet a unique possibility to probe the collective properties of a new state of dense matter, the quark-gluon plasma (see, e.g., [22–24]). The experiments at RHIC and the LHC have provided clear evidence that the production of hadrons in A–A collisions goes through the formation of a fireball of hot and dense quark-gluon plasma. This follows from the observation of strong suppression of high-\({{p}_{{\text{T}}}}\) particle spectra (the so-called jet quenching phenomenon expressed in the nuclear modification factor \({{R}_{{{\text{AA}}}}}\)) and from the results of hydrodynamic simulations of A–A collisions.

The main purpose of this work is to bring reader’s attention to an interesting possibility to probe the initial and final state effects in nucleus–nucleus collisions simultaneously, with a single measurement. This can be realised by introducing a novel observable, the double nuclear modification factor. Our note is organized as follows. First, we describe our theoretical approach. Then we show an interesting competition between the combinatorical enhancement in the DPS and the suppression due to parton energy losses. We illustrate it by the example of the associated production of \(J{\text{/}}\psi \) mesons and \(W\) bosons. Some further possible directions of studies are discussed in Section 4.

THEORETICAL SETUP

Let us consider nucleus–nucleus collisions at the LHC. The parton flux is enhanced by the number \(A\) of nucleons in each nucleus, and then—modulo (anti)shadowing effects in the nuclear parton distribution functions—the single-parton scattering (SPS) cross section is simply expected to be that of \(p\)–\(p\) collisions, or, more exactly, that of nucleon–nucleon collisions (N–N) scaled by the factor \({{A}^{2}}\), i.e., [25]:

$$\begin{gathered} \sigma _{{(AA \to a)}}^{{{\text{SPS}}}} = \sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\int {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}}){{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}} - {\mathbf{b}}){\kern 1pt} {{d}^{2}}{{{\mathbf{b}}}_{1}}{{d}^{2}}{\mathbf{b}} \\ = \sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\int {{{\text{T}}}_{{{\text{AA}}}}}({\mathbf{b}}){{d}^{2}}{\mathbf{b}} = {{A}^{2}}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}, \\ \end{gathered} $$
(1)

as long as all of final state effects are out of game. Here the vector b1 measures the distance in the transverse plain from the center of a nucleus to a given nucleon; \({{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}})\) is the nucleus thickness function which describes the nucleon density of a nucleus; the impact parameter vector b connects the centers of the colliding nuclei in the transverse plane; \({{{\text{T}}}_{{{\text{AA}}}}}({\mathbf{b}})\) is the standard nuclear overlap function normalised to A2, and \(\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\) is the single inclusive hard scattering cross section. The normalization constant A2 refers to the combinatorial number of possible N–N collisions as if the nucleon shadowing effects were neglected.

Traditionally, the level of the energy losses by a hard scattered parton or a particle a (the final state effects) is quantitatively characterized by the nuclear modification factor \({{R}_{{{\text{AA}}}}}(a)\):

$${{R}_{{{\text{AA}}}}}(a) = \frac{{{{\sigma }_{{(AA \to a)}}}}}{{{{A}^{2}}{{\sigma }_{{(NN \to a)}}}}} \approx \frac{{\sigma _{{(AA \to a)}}^{{{\text{SPS}}}}}}{{{{A}^{2}}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}}}.$$
(2)

The left equality gives the definition of the quantity \({{R}_{{{\text{AA}}}}}(a)\); the right equality is approximate, when the double parton scattering (DPS) processes are negligible. The physical meaning of \({{R}_{{{\text{AA}}}}}(a)\) is the survival probability for a particle produced in a nuclear medium. For a particle untouched by final state interactions (such as an electroweak boson, \(a = W,\;Z,\;\gamma \)) we evidently have \({{R}_{{{\text{AA}}}}}(a) = 1\).

We can generalize this nuclear modification factor to the case of two hard scattered partons by introducing a double nuclear modification factor:

$${{R}_{{{\text{AA}}}}}(ab) = \frac{{{{\sigma }_{{(AA \to ab)}}}}}{{{{A}^{2}}{{\sigma }_{{(NN \to ab)}}}}} \approx \frac{{\sigma _{{(AA \to ab)}}^{{{\text{SPS}}}}}}{{{{A}^{2}}\sigma _{{(NN \to ab)}}^{{{\text{SPS}}}}}},$$
(3)

where \(\sigma _{{(NN \to ab)}}^{{{\text{SPS}}}}\) and \(\sigma _{{(AA \to ab)}}^{{{\text{SPS}}}}\) are the inclusive cross sections to simultaneously produce two hard particles \(a\) and \(b\) in an \(N\)–\(N\) or \(A\)–\(A\) collision, respectively. Similarly to the case of single-particle inclusive production (1), we have a relation for associated \(ab\) production:

$$\begin{gathered} \sigma _{{(AA \to ab)}}^{{{\text{SPS}}}} = \sigma _{{(NN \to ab)}}^{{{\text{SPS}}}}\int {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}}){{T}_{{\text{A}}}}({{{\mathbf{b}}}_{1}} - {\mathbf{b}}){\kern 1pt} {{d}^{2}}{{{\mathbf{b}}}_{1}}{{d}^{2}}{\mathbf{b}} \\ = \sigma _{{(NN \to ab)}}^{{{\text{SPS}}}}\int {{{\text{T}}}_{{{\text{AA}}}}}({\mathbf{b}}){\kern 1pt} {{d}^{2}}{\mathbf{b}} = {{A}^{2}}\sigma _{{(NN \to ab)}}^{{{\text{SPS}}}}, \\ \end{gathered} $$
(4)

again as long as all of final state effects are out of consideration.

Under a reasonable assumption (approximation) that the produced particles a and b no longer interact with each other and fragment independently, we come to a naive expectation that the survival probability factorizes:

$${{R}_{{{\text{AA}}}}}(ab) = {{R}_{{{\text{AA}}}}}(a){{R}_{{{\text{AA}}}}}(b).$$
(5)

This may be not fully true in the real life. In the SPS case, the correlations are induced by the fact that the both particles are produced in the same point. As so, they either both have low survival probability if are produced in the inner part of a nucleus, or both have high survival probability if are produced near the surface. The particle survival probability may also depend on the kinematic variables. The particles may either both have large \({{p}_{{\text{T}}}}\) if are produced in a relatively hard collision, or both have smaller \({{p}_{{\text{T}}}}\) if are produced in a relatively soft collision. In view of this, we introduce a numerical prefactor in Eq. (5)

$${{R}_{{{\text{AA}}}}}(ab) = F{{R}_{{{\text{AA}}}}}{\text{(}}a){{R}_{{{\text{AA}}}}}(b)$$
(6)

with \(F = \mathcal{O}(1)\). Recall however, that for a particle untouched by final state interactions (\(a = W,Z,\gamma \)) we strictly have \({{R}_{{{\text{AA}}}}}(a) = 1\) and \({{R}_{{{\text{AA}}}}}(ab) = {{R}_{{{\text{AA}}}}}{\text{(}}b)\).

The topology of DPS events is more complex and more diverse. Here we have a collision of two pairs of partons at a time

$${{p}_{1}} + {{p}_{2}} \to a,\quad {{q}_{1}} + {{q}_{2}} \to b,$$
(7)

and the initial partons can be distributed among the nucleons in various ways. Accordingly, there are three different contributions showing different dependence on A. First, there is a configuration where the partons \({{p}_{1}}\) and \({{q}_{1}}\) are taken from the same nucleon, and the partons \({{p}_{2}}\) and \({{q}_{2}}\) are taken from another (single) nucleon. Second is a configuration where the partons \({{p}_{1}}\) and \({{q}_{1}}\) are taken from the same nucleon, while the partons \({{p}_{2}}\) and \({{q}_{2}}\) belong to two different nucleons. Third, the partons \({{p}_{1}}\), \({{q}_{1}}\), \({{p}_{2}}\), and \({{q}_{2}}\) can all be taken from four different nucleons.

The respective contributions to the cross section then read:

$$\begin{gathered} \sigma _{{(AA \to ab)}}^{{{\text{DPS}}{\text{,1}}}} = \sigma _{{(NN \to ab)}}^{{{\text{DPS}}}}\int {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}}){\kern 1pt} {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}} - {\mathbf{b}}){\kern 1pt} {{d}^{2}}{{{\mathbf{b}}}_{1}}{\kern 1pt} {{d}^{2}}{\mathbf{b}} \\ = \sigma _{{(NN \to ab)}}^{{{\text{DPS}}}}\int {{{\text{T}}}_{{{\text{AA}}}}}({\mathbf{b}}){\kern 1pt} {{d}^{2}}{\mathbf{b}} = {{A}^{2}}\sigma _{{(NN \to ab)}}^{{{\text{DPS}}}}, \\ \end{gathered} $$
(8)
$$\begin{gathered} \\ \sigma _{{(AA \to ab)}}^{{{\text{DPS}}{\text{,2}}}} = \frac{m}{2}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\sigma _{{(NN \to b)}}^{{{\text{SPS}}}} \\ \times \;\frac{{2(A - 1)}}{A}\int {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}}){\kern 1pt} {\text{T}}_{{\text{A}}}^{{\text{2}}}({{{\mathbf{b}}}_{1}} - {\mathbf{b}}){\kern 1pt} {{d}^{2}}{{{\mathbf{b}}}_{1}}{\kern 1pt} {{d}^{2}}{\mathbf{b}} \\ = \frac{m}{2}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\sigma _{{(NN \to b)}}^{{{\text{SPS}}}}{\kern 1pt} 2(A - 1)\int {\text{T}}_{{\text{A}}}^{2}({\mathbf{b}}){\kern 1pt} {{d}^{2}}{\mathbf{b}} \\ \approx \frac{m}{2}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\sigma _{{(NN \to b)}}^{{{\text{SPS}}}}{\kern 1pt} 2A{\kern 1pt} {{{\text{T}}}_{{{\text{AA}}}}}(0), \\ \end{gathered} $$
(9)
$$\begin{gathered} \\ \sigma _{{(AA \to ab)}}^{{{\text{DPS}}{\text{,3}}}} = \frac{m}{2}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\sigma _{{(NN \to b)}}^{{{\text{SPS}}}} \\ \times \;\frac{{{{{(A - 1)}}^{2}}}}{{{{A}^{2}}}}\int {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}}){\kern 1pt} {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{1}} - {\mathbf{b}}) \\ \times \;{{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{2}}{\text{)}}{\kern 1pt} {{{\text{T}}}_{{\text{A}}}}({{{\mathbf{b}}}_{2}} - {\mathbf{b}}){\kern 1pt} {{d}^{2}}{{{\mathbf{b}}}_{1}}{\kern 1pt} {{d}^{2}}{{{\mathbf{b}}}_{2}}{\kern 1pt} {{d}^{2}}{\mathbf{b}} \\ = \frac{m}{2}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\sigma _{{(NN \to b)}}^{{{\text{SPS}}}}{\kern 1pt} \frac{{{{{(A - 1)}}^{2}}}}{{{{A}^{2}}}}\int {\text{T}}_{{{\text{AA}}}}^{2}({\mathbf{b}}){\kern 1pt} {{d}^{2}}{\mathbf{b}} \\ \approx \frac{m}{2}\sigma _{{(NN \to a)}}^{{{\text{SPS}}}}\sigma _{{(NN \to b)}}^{{{\text{SPS}}}}{\kern 1pt} {{A}^{2}}{\kern 1pt} \frac{{{{{\text{T}}}_{{{\text{AA}}}}}(0)}}{2} \\ \end{gathered} $$
(10)

(\(m = 1\) if \(a = b\), and \(m = 2\) if a and b are different).

Now, collecting all the DPS contributions together and using the relation

$$\sigma _{{(NN \to ab)}}^{{{\text{DPS}}}} = \frac{m}{2} \cdot \frac{{\sigma _{{(NN \to a)}}^{{{\text{SPS}}}} \cdot \sigma _{{(NN \to b)}}^{{{\text{SPS}}}}}}{{{{\sigma }_{{{\text{eff}}{\text{,pp}}}}}}}$$
(11)

we get [25]:

$$\sigma _{{(AA \to ab)}}^{{{\text{DPS}}}} = {{A}^{2}}{\kern 1pt} \sigma _{{(NN \to ab)}}^{{{\text{DPS}}}} \cdot C$$
(12)

with [4]

$$C \approx 1 + \frac{{{{\sigma }_{{{\text{eff}}{\text{,pp}}}}}}}{{7[{\text{mb}}]\pi }}{{A}^{{1/3}}} + \frac{{{{\sigma }_{{{\text{eff}}{\text{,pp}}}}}{\kern 1pt} }}{{28[{\text{mb}}]\pi }}{{A}^{{4/3}}},$$
(13)

where the approximation applies to large nuclei.

The factor \(C\) in Eq. (13) indicates the enhancement in the DPS cross sections in \(A\)–\(A\) collisions compared to the corresponding A2-scaled values in nucleon-nucleon collisions. This enhancement amounts to \(C \sim 27\) (for small \(A = 40\)) or \(C \sim 215\) (for large \(A = 208\)). In all the estimations throughout this work we use the value of the effective DPS cross section \({{\sigma }_{{{\text{eff}}{\text{,pp}}}}} = 15\) mb.

Notably, the leading terms in Eq. (13) describe uncorrelated production of the particles a and b. Indeed, they are produced in different points and in different partonic subprocesses. So, these contributions must basically satisfy Eq. (5).

The double nuclear modification factor taking the SPS and DPS contributions together can finally be presented as:

$${{R}_{{{\text{AA}}}}}(ab) = {{R}_{{{\text{AA}}}}}(a){{R}_{{{\text{AA}}}}}(b)\left[ {F + \frac{{C - F}}{{K + 1}}} \right],$$
(14)

where we have introduced a shorthand notation

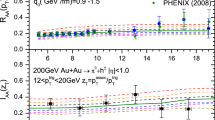
$$K = \sigma _{{(NN \to ab)}}^{{{\text{SPS}}}}{\text{/}}\sigma _{{(NN \to ab)}}^{{{\text{DPS}}}}.$$
(15)

As an example, Fig. 1 shows the behavior of K-factor for \(a = J{\text{/}}\psi \) and b = W.

Fig. 1.
figure 1

(Color online) K-factor versus the \(J{\text{/}}\psi \) transverse momentum. The bands show uncertainties in the cross section determination for \(J{\text{/}}\psi + W\) production.

Full size image

We are going to investigate this novel observable in its dependence on the type of hard particles (a and b) and on the kinematical region (mainly the transverse momenta). We can watch an interesting competition between the combinatorial enhancement C and the K‑ and RAA-suppressions.

NUMERICAL EXAMPLES

A specific interplay between the effects of DPS and jet quenching can be illustrated in the simplest case when one of the two hard particles does not lose its energy when passing through a dense matter. To be more solid, we can employ available experimental results on the associated production of two hard particles. Equations (11) and (15) enable us to extract the needed K-factor directly from the data without appealing to Monte Carlo simulations. As an example, consider the production of \(J{\text{/}}\psi \) mesons in association with a W boson. Relying on the measurements [26] performed by ATLAS collaboration, we obtain the K‑factor as a function of the \(J{\text{/}}\psi \) transverse momentum as shown in Fig. 1.

Since the W boson passes through the nuclear matter without losing energy, our main theoretical prediction (14) reduces to

$${{R}_{{{\text{AA}}}}}(J{\text{/}}\psi ,W) = {{R}_{{{\text{AA}}}}}(J{\text{/}}\psi )\left[ {1 + \frac{{C - 1}}{{K(J{\text{/}}\psi ,W) + 1}}} \right].$$
(16)

The combinatorial enhancement C does not depend on the process kinematics and the type of hard particles, but is mainly governed by the atomic number A. For the minimum bias Pb–Pb collisions this enhancement amounts to \(C \sim 215\). The measured nuclear \(J{\text{/}}\psi \) modification factor at the LHC [27–29] amounts to \({{R}_{{{\text{AA}}}}}(J{\text{/}}\psi ) \simeq 0.5\) at low transverse momenta (\({{p}_{{\text{T}}}} \simeq 2\) GeV/c) and to \({{R}_{{{\text{AA}}}}}(J{\text{/}}\psi ) \simeq 0.3\) over a wide interval of higher transverse momenta (\({{p}_{{\text{T}}}} > 5\) GeV/c). The “measured” \(K\)-factor demonstrates strong dependence on the transverse momentum: it changes from \( \sim {\kern 1pt} 1.4\) at \({{p}_{{\text{T}}}}\) lying in the interval [8.5–10] GeV/c to \( \sim {\kern 1pt} 374\) at \({{p}_{{\text{T}}}} \in \) 60–150 GeV/c. Thus we can expect that the production of \(J{\text{/}}\psi \) mesons in association with a W boson is not suppressed, but is enhanced in the region of moderate transverse momenta, contrary to unassociated (inclusive) \(J{\text{/}}\psi \) production. For \({{p}_{{\text{T}}}} \in \) 8.5–10 GeV/c, we have

$${{R}_{{{\text{AA}}}}}{\text{(}}J{\text{/}}\psi ,W) \simeq 30,$$

while \({{R}_{{{\text{AA}}}}}(J{\text{/}}\psi ) \simeq 0.3\)! In the region of high enough transverse momentum (\({{p}_{{\text{T}}}} > 60\) GeV/c), the behavior of W-associated \(J{\text{/}}\psi \) production converges to the unassociated case: \({{R}_{{{\text{AA}}}}}(J{\text{/}}\psi ,W) \simeq {{R}_{{{\text{AA}}}}}(J{\text{/}}\psi )\) since the ratio \((C - 1){\text{/}}(K + 1)\) becomes small. This example clearly demonstrates the competition between the effects of DPS (initial state effect) and jet quenching (final state effect).

The associated production of D mesons and W bosons shows yet a more intriguing behavior. In this case, there is a notable difference [30, 31] between the opposite-sign and same-sign production cross sections, and the K-factor is significantly larger for WD configurations of the opposite sign than for configurations of the same sign. The sensitivity of this factor to the charge configurations takes place also for other processes with \(W\) bosons in the final state [32–34]. The energy loss is independent of the sign of \(D\) mesons: \({{R}_{{{\text{AA}}}}}({{D}^{ + }}) \simeq {{R}_{{{\text{AA}}}}}({{D}^{ - }})\). It means that the double nuclear modification factor for the WD associate production will be notably larger for the same-sign configurations then for the opposite-sign ones:

$${{R}_{{{\text{AA}}}}}({{D}^{ \pm }},{{W}^{ \mp }}) < {{R}_{{{\text{AA}}}}}({{D}^{ \pm }},{{W}^{ \pm }}),$$

at the same kinematics.

CONCLUSIONS

We propose a novel observable, the double nuclear modification factor, to probe the initial and final state effects in nucleus–nucleus collisions at a time, “in one package.” An interesting competition between the combinatorial enhancement due to DPS and the suppression due to the parton energy losses can be observed. As an illustration we demonstrate that the production of \(J{\text{/}}\psi \) mesons in association with \(W\) bosons is not suppressed but is enhanced in the region of moderate transverse momenta, unlike the case of unassociated \(J{\text{/}}\psi \) production. At the same time, in the region of high enough transverse momenta the nuclear modification factor for associated \(J{\text{/}}\psi + W\) production converges to that of unassociated \(J{\text{/}}\psi \). In the production of \(D\) mesons associated with a \(W\) boson, the double nuclear modification factor will be larger for same-sign \(WD\) configurations then for opposite-sign ones at the same kinematics.

We come to the conclusion that measurements of the double nuclear modification factor potentially open a wide room for further studies of an interplay between the effects of DPS and jet quenching, extending to various types of hard final state particles in a wide interval of their transverse momenta.

The results discussed above assumed “minimum bias” \(A\)–\(A\) collisions without any selection in the reaction centrality. In the future one can also apply this study to different centrality classes. The required cross sections for the SPS and DPS events lying within a certain impact-parameter interval corresponding to a given centrality percentile may be found in [25].