INTRODUCTION

The diode effect in the superconducting structures (SDE) became one of the central topics in condensed matter physics [1]. Such effect has a massive potential for the application in the area of superconducting electronics [2] and spintronics [3, 4]. Since its first discovery in the superconducting superlattices [5], the SDE has been reported in many different structures, including junction-free devices [5–9], Josephson junctions [10–15], and certain more exotic systems [16]. There have been numerous theoretical propositions of the systems where superconducting diode effect can be observed, including bulk superconducting materials [17–22], bilayer structures [23, 24] and Josephson junctions [25–30].

One of the most promising platforms for the implementation of the SDE is topological insulator (TI) based diodes [9, 13, 31]. The surface of TI provides strong spin–orbit coupling (SOC) which makes it possible to demonstrate a substantial magneto-electric effect [32–34]. Special attention has been paid to the magneto-electric effect in the TI based Josephson junctions, where it reveals itself in the form of the anomalous ground state phase shift [26, 29, 35–49]. Recently, it has been demonstrated that in the TI hybrid structures where superconductivity and ferromagnetism are spatially separated, the ground state is also modified [50, 51]. In this case the ground state corresponds to the spatially inhomogeneous superconducting order parameter. This superconducting state is commonly referred as the helical state [52–57].

The superconducting helical state became one of the options in achieving the SDE [1, 19–21]. Described by finite Cooper pair momentum, the helical state can be realized in systems with broken inversion and time reversal symmetries. The former is connected to the appearance of the SOC term in the Hamiltonian, while the latter can be introduced by the magnetic field. In this case the direction of the Cooper pair momentum depends on the direction of the magnetic field. The finite momentum of the Cooper pair, which is locked to the direction of the magnetic field leads the nonreciprocal depairing current in various systems.

Here we discuss the consequences of the hexagonal warping of the TI surface states on the Josephson critical current and nonreciprocal transport in the S/TI/S system with an in-plane Zeeman field. The effect of hexagonal warping is important in the TI based devices, since it can significantly change some of the transport properties. For example, it is well known that the interference effects near the defects are strongly enhanced due to the deformation of the Fermi surface [58, 59]. The warping term also leads to the anisotropy of the spin conductivity in the TI materials [60]. The influence of the snowflake Fermi surface on superconducting properties in the hybrid structures has also been questioned [61–63]. However, the impact of the warping term on the superconducting transport and especially nonreciprocal transport have not been well studied.

We formulate the model in the framework of the tight-binding Bogoliubov–de Gennes (BdG) Hamiltonian and assume the nearest neighbour hopping approximation. Within the model we calculate the superconducting current–phase relations (CPR) and the Josephson critical current. First we show that the warping term causes the Josephson current anisotropy, i.e., the supercurrent depends on the orientation of the warped Fermi surface. We demonstrate that in the presence of the finite in-plane Zeeman field there is a Josephson current nonreciprocity between the two superconducting islands. This phenomenon is known as the superconducting Josephson diode effect [1]. As a next step we take into account the hexagonal warping of the TI Fermi surface which is inherent in certain 3D topological insulators [58]. We claim that the presence of the hexagonal warping leads to the anisotropy of the supercurrent nonreciprocity in the system under consideration. This is a direct consequence of the rotational symmetry breaking caused by the presence of the hexagonal warping.

THEORY

We start by formulating the theoretical model of the S/TI/S hybrid structure. Such system can be described by the following effective Hamiltonian [58, 64]:

$$\begin{gathered} H({\mathbf{k}}) = {{H}_{0}} + {{H}_{{SOC}}} + {{H}_{W}} + {{H}_{S}} + {{H}_{Z}} \\ = \left( {\frac{{{{\hbar }^{2}}}}{{2{{m}_{{{\text{eff}}}}}}}(k_{y}^{2} + k_{x}^{2}) - {{\mu }_{x}}} \right){{{\hat {s}}}_{0}} \otimes {{{\hat {\sigma }}}_{z}} \\ + \;\alpha \left( {{{k}_{y}}{{{\hat {s}}}_{x}} - {{k}_{x}}{{{\hat {s}}}_{y}}} \right) \otimes {{{\hat {\sigma }}}_{z}} + \lambda {{k}_{x}}\left( {k_{x}^{2} - 3k_{y}^{2}} \right){{{\hat {s}}}_{z}} \otimes {{{\hat {\sigma }}}_{z}} \\ + \;g{{\mu }_{B}}{\mathbf{B}} \cdot {\mathbf{\hat {s}}} \otimes {{{\hat {\sigma }}}_{z}} + \Delta {{{\hat {s}}}_{0}} \otimes {{{\hat {\sigma }}}_{x}}. \\ \end{gathered} $$
(1)

Here, \({{\mu }_{x}}\) is the chemical potential in the corresponding region (\(x = S\) for the superconducting region S and \(x = N\) for the bare topological insulator surface TI), \(\alpha \) is the strength of the spin–orbit coupling and \(\lambda \) is the warping coefficient. \({{\mu }_{B}}\) is the Bohr magneton and \({\mathbf{B}} = (0,{{B}_{y}},0)\) is the Zeeman field. The Zeeman field B is assumed to be finite in all the regions of the hybrid structure. The order parameter Δ(x) = \(\Delta {{e}^{{i{{\phi }_{2}}}}}\theta (x - {{d}_{n}}{\text{/}}2)\theta (x - {{d}_{n}}{\text{/}}2\) – ds) + \(\Delta {{e}^{{i{{\phi }_{1}}}}}\theta (x + {{d}_{n}})\theta (x\) + dn/2 + ds), where \(\Delta \) is a real-valued constant, \(\phi = {{\phi }_{2}} - {{\phi }_{1}}\) is the phase difference between the superconducting islands and \(\theta (x)\) is the Heaviside step function. The matrices \(\hat {s}\) and \(\hat {\sigma }\) are the Pauli matrices in the spin and particle–hole spaces, respectively. These spaces are combined by the Kronecker product \( \otimes \).

The Hamiltonian in Eq. (1) can describe both the surface and quasi-two-dimensional bulk states of the topological insulator [64]. The case of the surface states with a robust Dirac cone dispersion can be realized in the limit of \({{m}_{{{\text{eff}}}}} \to \infty \). On the other hand, when the quadratic term is not sufficiently small the model coincides with the two-dimensional electron gas with the Rashba spin–orbit coupling.

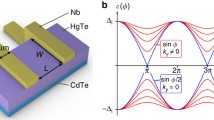
The system described by the Hamiltonian in Eq. (1) is depicted in Fig. 1. We use the tight-binding approximation of the continuum Hamiltonian in Eq. (1) with the lattice constant \(a = 2\) nm. To discretize the Hamiltonian we utilize the open-source software package Kwant [65] for the tight-binding transport simulations. It is important to emphasize that the hybrid structure under consideration is finite and two-dimensional, so that we do not take into account variations along the axis perpendicular to the junction plane. The lengths of the S regions are \({{d}_{{S1}}}\) and \({{d}_{{S2}}}\), the length of the non-superconducting region is \(L\) and the width of the Josephson junction is W. For simplicity we assume perfectly transparent S/TI interfaces.

Fig. 1.
figure 1

(Color online) (a) Schematic geometry of the Josephson diode based on the TI weak link. The superconducting layers S are assumed to be thin so that the system is effectively two-dimensional. \(\phi = {{\phi }_{2}} - {{\phi }_{1}}\) corresponds to the phase difference between the superconducting parts. \(\theta \) represents the angle of the Fermi surface rotation in the momentum space. (b) The tight-binding representation of the middle normal region. Here two-layer region with blue sites corresponds to the virtual self energy lead with hopping term \(t\) from the left to the right site.

Full size image

In order to calculate the supercurrent across the hybrid structure we employ the methodology developed in [66, 67]. Basically it makes use of the fact that Kwant software allows one to calculate the retarded Green’s function of the specified region. In this case we need to add the two-layer virtual self energy lead in the middle of the normal region shown in Fig. 1b. Then we compute the Green’s function corresponding to the self energy lead. The virtual self energy lead does not introduce any change to the system but is only necessary for calculation of the Green’s function and subsequently the supercurrent. The supercurrent can be written in the following form:

$$I = ie\left\langle {\sum\limits_{i \in L} \frac{{d{{n}_{i}}}}{{d\tau }}} \right\rangle = \frac{{ie}}{\hbar }\left\langle {\sum\limits_{i \in L} [c_{i}^{\dag }(\tau ){{c}_{i}}(\tau ),{{H}_{{{\text{lead}}}}}]} \right\rangle .$$
(2)

Here, \({{n}_{i}}\) is the number operator, \({{H}_{{{\text{lead}}}}}\) is the Hamiltonian of the virtual lead and \(\langle \rangle \) denotes the thermal average. \({{H}_{{{\text{lead}}}}}\) contains the hopping elements of the virtual lead and L denotes the sites of the lead. The supercurrent in the framework of the Green’s function in Matsubara representation takes the form

$$\begin{gathered} I = ie\sum\limits_{i \in L,j \in R} \left( {{{t}_{{ij}}}G{{{(\tau ,\tau {\kern 1pt} ')}}_{{ij}}} - {{t}_{{ji}}}G{{{(\tau ,\tau {\kern 1pt} ')}}_{{ji}}}} \right) \\ = ieT\sum\limits_{i \in L,j \in R} \sum\limits_n \left( {{{t}_{{ji}}}G{{{(i{{\omega }_{n}})}}_{{ij}}} - {{t}_{{ij}}}G{{{(i{{\omega }_{n}})}}_{{ij}}}} \right) \\ = - 4eT\sum\limits_n {\text{Im}}\left[ {{\text{Tr}}\left( {{{T}_{{RL}}}G{{{\left( {i{{\omega }_{n}}} \right)}}_{{LR}}} - {{T}_{{LR}}}G{{{\left( {i{{\omega }_{n}}} \right)}}_{{RL}}}} \right)} \right], \\ \end{gathered} $$
(3)

where we set \(\hbar = {{k}_{B}} = 1\). Here \({{T}_{{RL}}}\) (\({{T}_{{LR}}}\)) is the hopping matrix from right (left) to left (right). \(G\) is the Green’s function and \({{\omega }_{n}} = 2\pi T(n + 1{\text{/}}2)\) are the Matsubara frequencies. In the first equality \({{H}_{{{\text{lead}}}}}\) has been expanded in terms of the electronic operators and definition of the retarded Green’s function has been used, i.e., \(G{{(\tau ,\tau {\kern 1pt} ')}_{{ij}}} = \langle c_{i}^{\dag }(\tau ){{c}_{j}}(\tau {\kern 1pt} ')\rangle \) for \(\tau > \tau {\kern 1pt} '\). The second equality has been obtained using the inverse Fourier transform of the Green’s function and taking the limit \(\tau - \tau {\kern 1pt} ' \to {{0}^{ + }}\). For more details of the supercurrent derivation we refer the reader to the supplementary material of [66, 67].

To demonstrate the anisotropy effects introduced by the warping term in the total Hamiltonian of the system Eq. (1) one could follow two paths. One of the ways is to show the anisotropy by rotating the superconducting islands with respect to the TI surface, while keeping the direction of the Zeeman field fixed. Another way to perform the rotation is to introduce rotating angle in the k space and the corresponding unitary transformation to the Hamiltonian in the spin space. This can be represented by the following expressions

$$\begin{gathered} {{\left( {\begin{array}{*{20}{c}} {{{k}_{x}}} \\ {{{k}_{y}}} \end{array}} \right)}_{R}} = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{k}_{x}}} \\ {{{k}_{y}}} \end{array}} \right), \\ \hat {U} = \exp \left( { - i\theta {{{\hat {\sigma }}}_{z}}{\text{/}}2} \right), \\ \end{gathered} $$

where subscript \(R\) denotes the rotated k space with the angle \(\theta \) (Fig. 1). Simultaneously the transformation of the wave-vectors k must be accompanied by the rotation along the z-axis in the spin space \(\hat {U}\). With the above transformations we can replace rotating the TI surface in real space with the rotation in k space.

One of the crucial characteristics of the diode effect is the diode quality factor. In this work the conventional definition is used:

$$\eta = \frac{{I_{c}^{ + } - \,{\text{|}}I_{c}^{ - }{\text{|}}}}{{I_{c}^{ + } + \,{\text{|}}I_{c}^{ - }{\text{|}}}},$$
(4)

where \(I_{c}^{ + } = \max [I(\phi )]\) is the Josephson critical current in the positive direction and \(I_{c}^{ - } = \min [I(\phi )]\) is the Josephson critical current in the opposite direction.

In the following sections we discuss the CPR of the S/TI/S Josephson junction in the absence of the Zeeman field and the impact of the hexagonal warping on the critical current. Then we consider the nonzero Zeeman field and the arising anomalous ground state phase shift as well as the nonreciprical superconducting transport. Finally, we investigate the Josephson critical current nonreciprocity caused by the helical state and the influence of the warping term on the diode efficiency.

CURRENT–PHASE RELATIONS AND THE CRITICAL CURRENT AT \(B = 0\)

In this section we set the following parameters for the simulations: a = 2 nm, \(L = 60{\kern 1pt} \) nm, \({{d}_{{S1}}} = {{d}_{{S2}}}\) = 40 nm, \(T = 0.1{\kern 1pt} \) K, \({{\mu }_{S}} = {{\mu }_{N}} = 10{\kern 1pt} \) meV, g = 50, \(\alpha = \) 240 meV nm and λ = 100 meV nm3. Such values for α and for the strength of the warping \(\lambda \) are within the experimentally relevant range [58].

At the beginning we discuss the current–phase relations of the Josephson junctions in the case of zero Zeeman field B = 0. Such situation corresponds to the case of the nonmagnetic junction. In Figs. 2a and 2b the current–phase relations for the S/TI/S junction are demonstrated with the curves for different values of the width of the normal region W with zero warping term \(\lambda = 0\). From Fig. 2a we can see that supercurrent \(I(\phi )\) has the conventional sinusoidal shape in the short junction [68]. The coherence length in the system corresponds to the situation of the clean limit, i.e., \(\xi = \hbar {{{v}}_{f}}{\text{/}}\Delta \). Hence, for the parameters of this section with \(\Delta = 1\) meV the coherence length \(\xi \approx 156\) nm which means that the system is in the short junction limit in Fig. 2a. Figure 2b corresponds to the long junction limit since \(\xi \approx 32\) nm. However, there is an important feature of the such S/TI/S junction in the presence of the hexagonal warping (\(\lambda \ne 0\)). In Fig. 2c we demonstrate the Josephson critical current as a function of the Fermi surface rotation angle \(\theta \) computed at \(W = 40\) nm. We can see that the critical current strongly depends on the angle of the Fermi surface rotation. Such anisotropy of \({{I}_{c}}(\theta )\) is due to the hexagonal warping of the Fermi surface. Since the introduction of the warping term breaks the rotational symmetry, the Hamiltonian in Eq. (1) becomes invariant under rotation of \(\theta = 2n\pi {\text{/3}}\), however the spectrum of the Hamiltonian is invariant under \(\theta = n\pi {\text{/}}3\). As we can see from Fig. 2c the critical current is invariant under \(\theta = n\pi {\text{/}}3\) as well.

Fig. 2.
figure 2

(Color online) Current–phase relations of the S/TI/S Josephson junction in the absence of Zeeman field. (a) and (b) correspond to the CPR in the short (\(\Delta = 1{\kern 1pt} \) meV) and long (\(\Delta = 5{\kern 1pt} \) meV) junctions, respectively. The curves were calculated for three different values of the junction width W in the absence of the warping. (c) Polar plot of the Josephson critical current vs. the angle of the Fermi surface rotation \(\theta \) calculated for \(\lambda = 100\) meV nm3.

Full size image

THE GROUND STATE PHASE SHIFT AND THE SDE IN THE S/TI/S JUNCTION

In this section we set the following parameters for the simulations: a = 2 nm, \(L = 60{\kern 1pt} \) nm, \(W = 40{\kern 1pt} \) nm, \({{d}_{{S1}}} = {{d}_{{S2}}} = 40{\kern 1pt} \) nm, \(T = 0.1{\kern 1pt} \) K, \({{\mu }_{S}} = {{\mu }_{N}} = 10{\kern 1pt} \) meV, \(g = 50\), \(\alpha = 240\) meV nm, \(\lambda = 100\) meV nm3, \(\theta = 0\) and Zeeman field \({{B}_{y}} = 0.45{\kern 1pt} \) T, which corresponds to the Zeeman energy \(g{{\mu }_{B}}{{B}_{y}} \approx 1.3{\kern 1pt} \) meV.

Now we include a finite Zeeman field in the system. In our case we will consider the Zeeman field in all the hybrid structure. It is also possible to take it into account the field only in the normal part. In the latter case the results are not affected qualitatively, since the Zeeman field influences the superconducting regions via the mechanism of the proximity effect resulting in the quantitative difference [69]. As mentioned above, when the superconducting and magnetic orders are spatially separated the helical state and SDE still can be realized in the topological hybrid structures [50, 51].

In Fig. 3 we show the CPR of the Josephson junction in the presence of the in-plane Zeeman field \({{B}_{y}} = 0.45\) T. From the plots we can notice that finite field \({{B}_{y}}\) significantly modifies the CPR shifting the ground state phase to the non-zero value \({{\phi }_{0}}\). This means that the zero supercurrent between the two superconducting islands in the junction is no longer realized at \(\phi = 0\). \({{\phi }_{0}}\) is usually referred as the anomalous ground state phase shift of the Josephson junction [48]. Another important observation in Fig. 3 is the nonreciprocity of the Josephson critical current, i.e., the absolute value of the critical current in one direction is not equal to the one in the opposite direction (\(I_{c}^{ + } \ne I_{c}^{ - }\)). This is the Josephson diode effect. When the hexagonal warping is taken into consideration the CPR undergo some changes depending on the rotation angle of the Fermi surface \(\theta \). In Figs. 3c and 3d we demonstrate the CPR for \(\theta = 0\) and we can see that the nonreciprocity of the critical current is substantially suppressed. However, the ground state phase shift \({{\phi }_{0}}\) still remains finite.

Fig. 3.
figure 3

(Color online) CPR of the S/TI/S Josephson junction in the presence of in-plane Zeeman field \({{B}_{y}}\); (a) and (b) correspond to the case of \(\lambda = 0\), while (c) and (d) to \(\lambda = 100\) meV nm3 and \(\theta = 0\). \({{\phi }_{0}}\) is the ground state phase shift of the Josephson junction.

Full size image

In order to get more insight into the SDE, first we turn to the discussion of the diode efficiency for \(\lambda = 0\). In general, \(\eta \) is sensitive to many parameters of the system, however here we will discuss its dependence on the Zeeman field \({{B}_{y}}\) and the chemical potential of the non-superconducting area \({{\mu }_{N}}\). These parameters are believed to be controllable in the experimental setup, i.e., the Zeeman field can be set by the external magnetic field and \({{\mu }_{N}}\) can be tuned by the voltage biased gate in the normal region. We show these dependencies in Fig. 4 for two different values of \(\Delta \). We can see that the diode efficiency has an optimal value and changes sign at a certain value of \({{B}_{y}}\). In the framework of our model and for given parameters this sign-changing behavior is connected to the competition of the two helical bands for the contribution in supercurrent nonreciprocity. Indeed, two helical bands have the opposite helicities, i.e., the spins of quasiparticles corresponding to each band at a certain momentum direction are opposite to each other. Thus, for a given direction of the Zeeman field the helical bands compete with each other and the sign of \(\eta \) depends on whether one or the other band is dominant [19–21]. However, in general the sign-changing behavior of \(\eta \) is also possible in the case of a single helical band model (i.e., when \({{m}_{{{\text{eff}}}}} \to \infty \) in Eq. (1)) in long Josephson junctions [70].

Fig. 4.
figure 4

(Color online) Diode efficiency of the Josephson junction \(\eta \) as a function of Zeeman field \({{B}_{y}}\) (a) and chemical potential \({{\mu }_{N}}\) (b) calculated for two values of the pair potential: \(\Delta = 1{\kern 1pt} \) meV and \(\Delta = 5{\kern 1pt} \) meV.

Full size image

The plot of \(\eta ({{\mu }_{N}})\) dependence (Fig. 4b) illustrates that the diode efficiency can be tuned by the chemical potential of the central region as well. The reason for such behavior of \(\eta ({{\mu }_{N}})\) calculated at Δ = 1 meV can be attributed to small number of the low energy bound states in the junction and their nonmonotonic and quasi-periodic behavior as a function of \({{\mu }_{N}}\). Hence, such behavior of the bound states can vastly modify the superconducting current and specifically their contribution to the nonreciprocal transport.

ANISOTROPY OF THE DIODE EFFECT

In this section we set the following parameters for the simulations: \(a = 2{\kern 1pt} \) nm, \(L = 60{\kern 1pt} \) nm, \(W = 40{\kern 1pt} \) nm, \({{d}_{{S1}}} = {{d}_{{S2}}} = 40{\kern 1pt} \) nm, \(T = 0.1{\kern 1pt} \) K, \({{\mu }_{S}} = {{\mu }_{N}} = 10{\kern 1pt} \) meV, \(g = 50\), \(\alpha = 240\) meV nm, \(\lambda = 100\) meV nm3 and Zeeman field \({{B}_{y}} = 0.45{\kern 1pt} \) T. As we showed above the consideration of the warping term results in the anisotropy of the critical current. It is natural to assume that the diode efficiency also undergoes some similar changes. In Fig. 5a we illustrate the dependence as a function of \({{B}_{y}}\) at \(\lambda = 100\) meV nm3 for three different values of the Fermi surface rotation angle \(\theta \). We observe that while for a certain value of \({{B}_{y}}\) at \(\theta = 0\) the efficiency of the SDE can be almost zero, at \(\theta = \pi {\text{/}}6\) it can be dramatically increased up to more than \(\eta = 0.2\). This circumstance opens additional ways of incorporating such device in the field of superconducting electronics, enabling a new way of controlling the topological insulator based Josephson junctions. In Fig. 5b we further demonstrate how the diode efficiency is affected if \(\theta \) is varied. From the plot we can see that \(\eta \) is indeed anisotropic with a period in \(\theta \) of π/3, which is shown schematically by the rotating Fermi surfaces in the upper part of the figure. Fermi surfaces in the upper part of Fig. 5.

Fig. 5.
figure 5

(Color online) (a) Diode efficiency of the Josephson junction \(\eta \) as a function of Zeeman field \({{B}_{y}}\) for three different values of \(\theta \): \(\theta = 0\), \(\theta = \pi {\text{/}}12\) and \(\theta = \pi {\text{/}}6\). (b) \(\eta \) as a function of the rotation angle \(\theta \) calculated for two values of \(\Delta \): \(\Delta = 1{\kern 1pt} \) meV and \(\Delta = 5{\kern 1pt} \) meV. The insets show schematic cross sections of the Fermi surface.

Full size image

CONCLUSIONS

In this work we have discussed the superconducting diode effect in S/TI/S hybrid structure with the warped TI Fermi surface. Employing the tight-binding approximation of the Bogoliubov–de Gennes equations we have formulated the model in the clean limit. Within the formalism of the Green’s functions in the Matsubara representation we have computed the current–phase relations through the Josephson junction. First, we have demonstrated that the Josephson critical current itself is anisotropic, i.e., it depends on the orientation of the warped Fermi surface with respect to the S/TI interface. Then we have added the in-plane Zeeman field to the system and showed the emergence of the ground state phase shift in the CPR as well as substantial current nonreciprocity in the junction (diode effect). Inclusion of the warping term in the Hamiltonian may lead to the significant reduction of the current nonreciprocity for some orientations of the Fermi surface, however the ground state phase shift tends to remain finite. Finally, we have computed the angle dependence of the diode efficiency and demonstrated that diode effect can be remarkably anisotropic. This fact may be useful for the development of the superconducting diodes as it suggests additional method of control of the diode effect.