Self-Focusing and Self-Phase Modulation of a Focused Femtosecond Laser Beam in Fused Silica at Near-Critical Peak Power

Self-focusing and self-phase modulation of focused femtosecond laser pulse were studied in bulk fused silica. Depending on pulse energy magnitude, three different regimes were observed in the experiment: (1) linear regime, when the self-focusing effect is insignificant, characterized by linear spectral broadening; (2) transition regime, when the self-focusing effect notably reduces a laser beam spot in a focal plane without considerable nonlinear absorption and beam collapse, characterized by quick increase in spectral broadening due to self-phase modulation; (3) nonlinear regime, filamentation, characterized by near-to- linear spectral broadening due to self-phase modulation. The slope for the linear and nonlinear regimes was the same within the measurement error bars. The numerical simulation, using the ray transfer matrix method, envisioned the self-phase modulation spectral broadening effect in all these regimes.

Ultrafast optical and laser technology have a great progress in the last decades and became a widespread thing in different fundamental and applied fields, such as materials processing [1], spectroscopy [2], atmosphere sensing [3], and others. An application of ultrashort high-intensive laser pulses has some peculiarities due to effects caused by Kerr nonlinearity of a propagation medium. Majorly, they are self-focusing (SF), self-phase modulation (SPM), and a filamentation as a complicated action of several nonlinear effects [4, 5]. Frequently these effects are undesirable, and special techniques, such as chirped pulse amplifications [6], are used to suppress them. However, they have several useful applications, for example, SPM effect is used for laser pulse duration shortening via spectrum broadening (post-compression) [7]. SPM can produce a coherent octave-spanning supercontinuum [8] exactly what is required for remote multicomponent gas analysis. The SPM broadening is also used for seeding optical parametric amplifiers [9] or Raman amplifiers [10]. Also, SPM can be used to estimate a magnitude and nature of Kerr-nonlinearity [11, 12]. All these applications require correct knowledge about SPM, SF and filamentation.

Despite the great progress of Kerr-nonlinearity effects investigation (see review papers [4, 5]), they are still under active investigation due to complex diverse actions in different media and conditions, especially for focused laser beams [13–16]. Sometimes tightly focused ultrashort laser pulse in a medium is considered in terms of “microscale filamentation” [13]. However, in [14, 15] a strong difference in the active physical mechanisms between high-NA and low-NA focusing was found. In [15] it was demonstrated that intensity clamping and thus electron density clamping do not occur at the strong laser beam focusing ($NA = 0.03$). In [16] the self-cleaning phenomenon indicating on the filamentation disappeared completely at $NA > 0.015$. Thus, propagation of focused laser pulses with the same energy/power can be in linear and nonlinear regimes at different $NA$ in the same material.

Previously, we studied focused femtosecond laser beam filamentation as a constructive interference of stimulated Raman scattering and SPM effects observed in BaWO₄ crystal [10, 17]. In this work, we investigate filamentation, SPM and SF effects of a focused ($NA = {{R}_{{1/{{e}^{2}}}}}{\text{/}}F \simeq 0.02$) femtosecond laser pulse in fused silica. Compared to [14–16], switching between linear and nonlinear focusing regimes was driven by a variation of laser pulse power near the self-focusing critical power. The fused silica (quartz) was selected as a popular material with the well-known magnitude and origin of Kerr nonlinearity.

The experiment was carried out with the second harmonic radiation of Yb-fiber laser (Satsuma, Amplitude systems). The laser pulse of 300 fs FWHM duration had central wavelength λ = 515 nm, output energy up to ${{E}_{p}} = 1.8$ μJ, laser beam diameter was 1.7 mm (level 1/e²), and pulse repetition rate was 1 kHz. The pulse energy was varied by detuning the second harmonic crystal from phase-matching. The laser operated on the fundamental TEM00 mode with energy instability of 0.5%. The laser beam was focused by a lens with a focal length f = 40 mm ($NA \simeq 0.02$) into the middle of 1-cm fused silica sample (Fig. 1). The focusing geometry was the same as in the experiments on the constructive interference of stimulated Raman scattering and SPM effects in BaWO₄ crystal [10, 17] which provided the highest efficiency of this effect [18]. The laser beam transmitted through the sample was attenuated by reflections from wedges (not shown on Fig. 1) and passed through a lens $f =$ 90 mm for a diagnostic: spectrum, energy and spatial profile. The laser pulse spectrum was measured by the spectrometer (ASP-150 FT, spectral resolution 0.03 nm, Avesta Project Ltd.). The laser beam profile and laser pulse energy were measured by a CCD camera (Spiricon SP-620U) and an Ophir PD10-C energy meter, respectively.

Fig. 1.

(Color online) Optical scheme of the experiment.

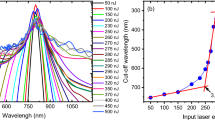
Examples of the measured spectra and beam intensity profiles of the pulses after the sample are shown in Fig. 2 for several pump pulse energies. The spectra demonstrate roughly symmetric broadening with a gradual energy increase that was caused by SPM effect. Besides spectrum broadening, the laser beam spot had a constriction at ${{E}_{p}} > 0.3$ μJ that indicated on additional focusing by SF. A background in the beam profile appeared at laser pulse energies above 0.5 μJ which can be clearly seen in Fig. 2 at higher energy ${{E}_{p}} = 1.2$ μJ. The background appearance was associated with a plasma formation causing beam scattering. The observed laser beam profile at ${{E}_{p}} > 0.5$ μJ was typical for a filamentation regime (nonlinear focusing) [15].

Fig. 2.

(Color online) Spectra and beam profiles of the laser pulse transmitted through fused silica sample at different incident pulse energy (see signs in the figure).

The spectral width measured at a slow gradual pump pulse energy increase is presented in Fig. 3a. Also transmitted pulse energy (the sample transmittance) was concurrently measured and presented in Fig. 3b. In Fig. 3a we can designate three domains with different behavior of the spectral width on pump pulse energy. The first corresponds to ${{E}_{p}}$ range 0–0.3 μJ which is associated with linear laser pulse traveling. Detectable spectral broadening appeared at ${{E}_{p}} \simeq 0.2$ μJ, and at ${{E}_{p}} = 0.2{-} 0.3$ μJ, the spectral broadening had a linear trend with pump pulse energy which is in coincidence with the known theory of SPM.

Fig. 3.

(Color online) (a) Spectrum width of (circles) Stokes and (squares) anti-Stokes wings of the laser pulse transmitted through fused silica sample versus the incident pulse energy; dashed lines are interpolation of linear regions of the dependence. Segments 1–3 indicate domains with different behavior of the dependence. (b) Transmitted pulse energy vs incident pulse energy.

The second energy domain ${{E}_{p}} = 0.3{-} 0.5$ μJ is characterized by a quick increase in spectral width, which indicates an intensity increase due to nonlinear (self-) focusing activation. The SF activation was confirmed by changing in the laser beam profile (see Fig. 2). However, in this energy range (${{E}_{p}} = 0.3 {-} 0.5$  μJ), nonlinear absorption (and plasma formation, respectively) was not detected, see the transmittance in Fig. 3b. Thus, the second domain corresponds to the case when nonlinear sub-focusing increased the radiation intensity resulting to enhanced SPM broadening without activation of nonlinear absorption. To the best of our knowledge, that is the first demonstration of this effect at sub-critical self-focusing power.

The third domain ${{E}_{p}} > 0.5$ μJ is characterized near-to-linear trend of increase in spectral width which takes place at laser pulse power above critical power of self-focusing (P_cr). At a power higher than the critical one, self-focusing prevails over diffraction and, accordingly, the intensity increases sharply and nonlinear absorption is observed, which leads to the formation of a plasma and subsequent refraction on it. The combined action of these effects leads to the formation of a filament and intensity stabilization. This regime is well studied [4, 5], however, we have to note the interesting and important point: the slope in Fig. 3a for the first (linear) and third (nonlinear) regimes are the same within measurement errors. This fact is not obvious because spatial and longitude intensity distribution is significantly transformed in the nonlinear regime. So, the slope in a dependence of SPM broadening on incident pulse energy can be used for nonlinear refractive index determination under filamentation of focused laser pulse if a contribution of other nonlinear effects, such as self- steepening [19], is insignificant. However, the SPM broadening under filamentation has increased measurement error due to its instability.

To verify the experimental results, a numerical simulation of the focused laser beam profile and corresponding SPM spectrum broadening in the fused silica was performed. Since the laser operated on the fundamental TEM00 mode, the laser intensity was considered as Gaussian:

$$I(r,t) = {{I}_{0}}\exp \left( { - \frac{{2{{r}^{2}}}}{{r_{0}^{2}}}} \right)\exp \left( { - \frac{{4\ln 2{\kern 1pt} {{t}^{2}}}}{{T_{{{\text{FWHM}}}}^{{\text{2}}}}}} \right),$$

(1)

where ${{r}_{0}} = 0.85$ mm is the beam radius at 1/e² level, ${{T}_{{{\text{FWHM}}}}} = 0.3$ ps is the FWHM pulse duration, ${{I}_{0}}$ is the peak intensity calculated as

$${{I}_{0}} = \frac{E}{{(\pi r_{0}^{2}{\text{/}}2){{T}_{{{\text{FWHM}}}}}\sqrt {\frac{\pi }{{\ln 16}}} }}.$$

(2)

In the linear regime of focusing when the beam focus in the sample center (z = 0), ${{I}_{0}}$ depends on a coordinate z as

$${{I}_{0}}(z) = \frac{{{{I}_{{\max }}}}}{{1 + {{{(z{\text{/}}{{z}_{{{\text{dif}}}}})}}^{2}}}},$$

(3)

where ${{z}_{{{\text{dif}}}}} = \pi nw_{0}^{2}{\text{/}}\lambda$ is the diffraction length for a beam with a radius ${{w}_{0}}$ (level 1/e²) in fused silica.

In a nonlinear regime, the radiation profile changes due to self-focusing. In air, self-focusing does not make a significant contribution, since the self-focusing critical power in air (${{P}_{{{\text{cr}}}}} \sim {{10}^{9}}$ W, which corresponds to a laser pulse energy of 0.4 mJ for our laser system) is much higher than the pulse energy/power in our experiment. Thus, after passing through the lens (f = 40 mm) and the distance z = 36.43 mm (linear focus position coincides with sample center), the beam size and the front curvature will be equal to:

$$w = {{r}_{0}}\sqrt {{{{(1 - z{\text{/}}f)}}^{2}} + {{{(z{\text{/}}{{z}_{d}})}}^{2}}} ,$$

(4)

$$R = {{z}_{d}}\frac{{{{{(1 - z{\text{/}}f)}}^{2}} + {{{(z{\text{/}}{{z}_{d}})}}^{2}}}}{{z{\text{/}}{{z}_{d}} - z(1 - z{\text{/}}f){\text{/}}f}},$$

(5)

where ${{z}_{d}} = \pi r_{0}^{2}{\text{/}}\lambda$ is the diffraction length for the initial beam. For further propagation description, the matrix optics was used with the initial complex radius of curvature:

$${{q}_{0}} = {{\left( {\frac{1}{R} + i\frac{\lambda }{{\pi {{w}^{2}}}}} \right)}^{{ - 1}}}.$$

(6)

Refraction at the air/fused silica interface corresponds to ${{q}_{{{\text{ref}}}}} = n{{q}_{0}}$ and for finding the new front curvature and beam radius:

$$R = {\text{Re}}{{\left( {\frac{1}{{{{q}_{{{\text{ref}}}}}}}} \right)}^{{ - 1}}},\quad r = \sqrt {\frac{\lambda }{{\pi n}}\frac{1}{{{\text{Im}}\left( {\frac{1}{{{{q}_{{{\text{ref}}}}}}}} \right)}}} .$$

(7)

The nonlinear phase shift in fused silica during propagation over distance dz is equal to ${{\varphi }_{{nl}}} = {{k}_{0}}{{n}_{2}}Idz$, where ${{k}_{0}} = 2\pi {\text{/}}\lambda$, n₂ is the nonlinear refractive index, and due to the intensity dependence on the radius, self-focusing occurs. Near the propagation axis, the radial exponential term can be expanded into a series, and then the nonlinear phase shift which depends on the radial coordinate, will have the form φ_nl = ${{k}_{0}}{{n}_{2}}{{I}_{0}}{\text{exp}}\left( { - \frac{{4{\text{ln}}2{{t}^{2}}}}{{T_{{{\text{FWHM}}}}^{2}}}} \right)\frac{{2{{r}^{2}}}}{{{{w}^{2}}}}dz$, which coincides with the phase ${{\varphi }_{{{\text{lens}}}}} = \frac{{k{{r}^{2}}}}{{2F}}$ introduced by the converging lens with focusing distance $F = \frac{{n{{w}^{2}}}}{{4{{n}_{2}}{{I}_{0}}dz}}$. By dividing the length of the sample into steps, so that the nonlinear phase shift does not exceed π/100, and replacing the self-focusing effect on a lens with the appropriate propagation matrix $\left( {\begin{array}{*{20}{c}} A&B \\ C&D \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1 - \frac{{dz}}{F}}&{dz} \\ { - \frac{1}{F}}&1 \end{array}} \right)$ and q_out = $\frac{{A{{q}_{{{\text{in}}}}} + B}}{{C{{q}_{{{\text{in}}}}} + D}}$ we can calculate the propagation through the sample. When laser pulse power exceeds the critical self-focusing power, self-focusing prevails over diffraction and the beam collapses at some distance, therefore it is possible to describe the change in the beam shape inside the fused silica only up to a collapse coordinate. The collapse coordinate was determined by reaching an intensity of 10¹³ W/cm² which is a typical value for a filament in the fused silica [20, 21]. To the best of our knowledge, the ray transfer matrix method was not previously applied to describe SF, therefore we checked this approach for a collimated beam. In order to self-focusing prevails over diffraction at the self-focusing critical power (P_cr = $3.77{{\lambda }^{2}}{\text{/}}(8\pi {{n}_{0}}{{n}_{2}})$), the effective focal length should be equal to $F = \frac{{n{{w}^{2}}}}{{4{{n}_{2}}{{I}_{0}}dz}}{{k}_{{{\text{eff}}}}}$, where ${{k}_{{{\text{eff}}}}} = 3.77$. It should be noted that this coefficient does not depend on an initially collimated beam diameter, linear and nonlinear refractive index of a medium.

Also we compared our calculation results with those in [22], where an expression, relating pulse energy and peak intensity of a focused laser beam with the SF account, is presented:

$$E = \frac{{I\tau {{\lambda }^{2}}}}{{\pi {{{(NA)}}^{2}} + I{{\lambda }^{2}}{\text{/}}{{P}_{{{\text{cr}}}}}}}.$$

(8)

To obtain a dependence of intensity in a beam focus on laser pulse energy, we transformed (8) to the following form:

$${{I}_{{{\text{max}}}}} = \frac{{{{E}_{p}}\pi {{{(NA)}}^{2}}}}{{{{\lambda }^{2}}(\tau - {{E}_{p}}{\text{/}}{{P}_{{{\text{cr}}}}})}}.$$

(9)

The dependence of intensity in the beam focus ($NA = 0.021$) calculated by the ray transfer matrix method and by using (9), are presented in Fig. 4a, where we see adequate agreement for both these methods. In contrast, if just linear focusing (line 3) is taken into account at the near-critical peak power magnitudes, in Fig. 4a there is large discrepancy in the simulated focal intensity values.

Fig. 4.

(Color online) (a) Calculated focal intensity in the fused silica sample versus the laser pulse energy according to (1) the ray transfer matrix method, (2) Eq. (9), and (3) linear propagation. (b) Beam radius versus the coordinate inside the fused silica sample. Radiation propagates from left to right and z = 0 corresponds to the center of the sample.

Using the ray transfer matrix method, we calculated a dependence of laser beam radius on coordinate z in the fused silica taking into account initial focusing by a lens f = 40 mm. For the focused laser beam, it was found that there are different cases of propagation depending on the laser radiation power. At low power, when the Kerr nonlinearity does not have a significant effect, the radiation propagation is linear (Fig. 4b, dashed line). With a gradual laser power increase to the critical self-focusing power, the contribution of the Kerr nonlinearity increases and the beam radius decreases comparing to the linear propagation case. At $0.8{{P}_{{{\text{cr}}}}}$ power, focal beam radius was $\simeq {\kern 1pt} 2$ times less than in the linear regime due to SF (Fig. 4b, solid line). At powers greater than the critical self-focusing power, the beam collapses before the geometrical focus and the calculation was stopped at this coordinate.

To calculate the spectrum broadening, we use the following approach. Propagation in a medium with a nonlinear refractive index ${{n}_{2}}$ over a distance of dz leads to the nonlinear phase shift $\delta \varphi = {{k}_{0}}{{n}_{2}}I(t)dz$, which leads to the appearance of new frequencies

$$\begin{gathered} \delta \omega = - \frac{{\partial \delta \varphi }}{{\partial t}} = - {{k}_{0}}{{n}_{2}}dz\frac{{\partial I}}{{\partial t}} \\ = {{k}_{0}}{{n}_{2}}dz{{I}_{0}}{\kern 1pt} \frac{{8\ln 2t}}{{T_{{{\text{FWHM}}}}^{2}}}{\kern 1pt} \exp \left( {\frac{{ - 4\ln 2{{t}^{2}}}}{{T_{{{\text{FWHM}}}}^{2}}}} \right), \\ \end{gathered} $$

(10)

and the broadening maximum is realized at $\frac{{\partial \delta \omega }}{{\partial t}} = 0$, which corresponds to $t = \pm \frac{{{{T}_{{{\text{FWHM}}}}}}}{{\sqrt {8\ln 2} }}$ and |δω_max| = ${{k}_{0}}{{n}_{2}}{{I}_{0}}dz\sqrt {8{\text{ln}}2{\text{/}}e} {\text{/}}{{T}_{{{\text{FWHM}}}}}$, where ${{I}_{0}} = {{I}_{0}}(z)$ due to the presence of a focusing lens (linear regime) and self-focusing inside the sample (nonlinear). Then the broadening over the whole sample length will be:

$$\Delta {{\omega }_{{\max }}} = \frac{{{{k}_{0}}{{n}_{2}}\sqrt {8\ln 2{\text{/}}e} }}{{{{T}_{{{\text{FWHM}}}}}}}\int\limits_0^l {{{I}_{0}}} dz,$$

(11)

for the linear regime, it can be analytically calculated:

$$\begin{gathered} \Delta {{\nu }_{{\max }}}[{\text{c}}{{{\text{m}}}^{{ - 1}}}] \\ = \frac{{16\ln 2{\kern 1pt} \sqrt {2{\text{/}}\pi e} n{{n}_{2}}E}}{{T_{{{\text{FWHM}}}}^{{\text{2}}}{{\lambda }^{2}}c}}\arctan \left( {\frac{l}{{2{{z}_{{{\text{dif}}}}}}}} \right). \\ \end{gathered} $$

(12)

For P near P_cr, we considered two cases: (1) $P < {{P}_{{{\text{cr}}}}}$; (2) $P \geqslant {{P}_{{{\text{cr}}}}}$. For the first case, we use the dependence of intensity on the z coordinate inside the sample obtained directly by the above-presented ray transfer matrix method. In the second case, the sample length was divided into three sections: (1) before beam collapse; (2) filament (the distance between nonlinear and linear foci, see Fig. 4b); (3) after linear focus. In the first section, we used the ray transfer matrix method. In the second section, we estimate $\int I(z)dz$ as ${{I}_{{{\text{filament}}}}} \times {{L}_{{{\text{filament}}}}}$ where the average intensity in the filament ${{I}_{{{\text{filament}}}}}$ is an order of $\sim {\kern 1pt} {{10}^{{13}}}$ W/cm² [20, 21]. After the linear focus, we considered the nonlinear phase shift as in the first section taking into account power reduction in the filament (multiplied by the transmittance, see Fig. 3b).

The calculation of SPM spectrum broadening on pulse energy was performed at a variation of n₂ and ${{I}_{{{\text{filament}}}}}$ values. The values ${{n}_{2}} = 1.7 \times {{10}^{{ - 16}}}$ cm²/W and ${{I}_{{{\text{filament}}}}} = 1.3 \times {{10}^{{13}}}$ W/cm² were found at which the spectrum broadening dependence on pulse energy is described the experiment in the best way (solid line in Fig. 5). The variation of n₂ affected on a position of the inflection point ${{E}_{{{\text{in}}}}} \sim 0.5$ μJ (energy of a pulse collapse), the variation of ${{I}_{{{\text{filament}}}}}$ affected on a height of this point (spectral broadening before collapse). These values are in good agreement with experimental ones for n₂ [23] and ${{I}_{{{\text{filament}}}}}$ [20, 21]. Also, the calculation confirms that at $P > {{P}_{{{\text{cr}}}}}$ the slope of the spectrum broadening dependence on pulse energy is close to one for the linear regime (described by (12)), but an additional spectral shift takes place due to spectrum broadening outside of the filament.

Fig. 5.

(Color online) (Solid line) Calculated and (points) experimental spectral width of the laser pulse transmitted through the fused silica sample versus the incident pulse energy. The dashed line corresponds to the slope for the linear regime.

The dependence of the integral $\int I(z)dz$ at $P > {{P}_{{{\text{cr}}}}}$ is presented in Fig. 6 for filament and whole sample length. Here we would note that in the nonlinear regime, a growth in spectral broadening with energy increase is majorly in the filament, while that is almost the same outside of the filament.

Fig. 6.

(Color online) Spectrum broadening in the filament and in the whole sample versus the laser radiation power.

In this study, we experimentally and numerically explored the nonlinear effect of self-focusing and self-phase modulation of 300-fs 515-nm focused ($NA\, \simeq \,0.02$) laser pulses in fused silica depending on laser pulse power near the critical power of self-focusing. Three different regimes were revealed in our experiments, depending on the peak pulse power: (1) linear focusing regime ($P < 0.6{{P}_{{{\text{cr}}}}}$), when self-focusing is insignificant and minor self-phase modulation-based spectral broadening increases linearly; (2) transitional regime ($0.6{{P}_{{{\text{cr}}}}} < P < {{P}_{{{\text{cr}}}}}$), when self-focusing considerably reduces the focal laser aperture, still without notable nonlinear absorption and beam collapse, while accompanied by a step-like increase in spectral broadening; (3) nonlinear regime ($P > {{P}_{{{\text{cr}}}}}$), when self-focusing prevails over diffraction and filamentation occurs, with the nearly linear increase in spectral broadening. The spectral broadening slopes for the linear and nonlinear regimes were the same within measurement errors and could be quantitatively simulated by the ray transfer matrix method.