Transport Properties of the Magnetic Topological Insulators Family (MnBi₂Te₄)(Bi₂Te₃)_m (m = 0, 1, …, 6)

Systematic studies of magneto-transport properties of the whole (MnBi₂Te₄)(Bi₂Te₃)_m family of magnetic topological insulators ($m = 0,1,...,6)$ have been carried out. Temperature dependences of the resistivity, magnetoresistance and the Hall effect at low temperatures have been studied. When m increases, i.e., when the separation between 2D MnBi₂Te₄ magnetic layers becomes larger, the transition from antiferromagnetic to ferromagnetic state takes place. We have found that ferromagnetic state survives even in the samples with $m = 6$, when 2D magnets are separated by six non-magnetic Bi₂Te₃ blocks.

After discovery [1–5] of the first antiferromagnetic (AFM) topological insulator (TI) MnBi₂Te₄, a large family of intrinsic magnetic TIs in the homologous series of compounds (MnBi₂Te₄)(Bi₂Te₃)_m were intensively studied [6–11]. These are layered crystals which consist of the 2D ferromagnetic (FM) septuple layer blocks of MnBi₂Te₄ for $m = 0$, and the periodic set of septuple and m non-magnetic quintuple layer blocks of Bi₂Te₃ for $m > 0$. Magnetic and electronic transport properties of these materials depend strongly on the m value and are thus highly tunable. While [1, 2, 6] apart from the theoretical calculations, were mainly focused on the experimental studies of the surface electronic structure (using ARPES,) and bulk magnetism (using magnetometry) for $m = 0,1,...,4$, other studies considered magneto-transport properties of $m = 0,1,...,3$ compounds: MnBi₂Te₄ [11, 14], MnBi₄Te₇ [14, 15], MnBi₆Te₁₀ [14, 15], MnBi₈Te₁₃ [16]. However, to the best of our knowledge, the magneto-transport studies of the whole (MnBi₂Te₄)(Bi₂Te₃)_m family, i.e., for $m = 0,1,...,6$, [7, 11, 17] till now are absent. Here we present for the first time the systematic studies of magneto-transport properties of this family with $m = 0,1,...,6$, namely, the temperature dependences of the resistivity $R(T)$, magnetoresistance ${{R}_{{xx}}}(H)$ and the Hall effect ${{R}_{{xy}}}(H)$ at low temperatures.

The transport and magneto-transport properties were studied on the samples of (MnBi₂Te₄)(Bi₂Te₃)_m, obtained by cleaving from an ingot, grown by the melt crystallization method. The samples were preliminarily selected and characterized by both X-ray and Raman spectroscopy analysis at room temperature, the results of these investigations were published earlier in [8, 11, 17]. The characteristic sizes of the samples were about 2 × 1 × 0.1 mm. The contacts were prepared with conducting graphite paste. The samples were mounted in the variable temperature insert immersed into the liquid helium cryostat with a superconducting solenoid. The field was always oriented perpendicular to the sample planes. The measurements of the sample resistance were carried out using the standard four-probe technique by a lock-in detector at 20 Hz alternating current in the temperature range (1.4–300) K.

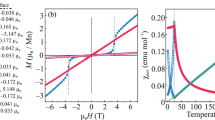
The temperature dependence of the sample MnBi₂Te₄ resistance is presented in Fig. 1a. This sample consists of septuple layer blocks only and doesn’t contain quintuple layer blocks, i.e., it corresponds to the case $m = 0$. One can see the sharp peak at Neel temperature ${{T}_{N}} = 25.3{\kern 1pt}$ K, which is due to the AFM ordering between neighboring septuple layer blocks. Figure 1b shows how the temperature of the magnetic ordering depends on the number of quintuple blocks m in the crystal. For $m = 1$ the characteristic critical temperature falls down to 13.2 K, then it decreases monotonously saturating to about 11 K for $m \geqslant 4$. We have found that the critical transition temperature for the samples with the same m value may be slightly different depending on the sample quality. In Fig. 1 we present the curves obtained on our samples with the highest transition temperature.

Fig. 1.

(Color online) Temperature dependences of the sample (MnBi₂Te₄)(Bi₂Te₃)_m resistance for $m = 0,1,...6$. The curves in (b) are specially scaled and shifted along the vertical axis for more convenient presentation, $m$-value increases from the top curve to the bottom one from 1 to 6.

The application of the magnetic field shifts the resistance peak and, finally, washes out this peculiarity. In MnBi₂Te₄ ${{T}_{N}}$ goes down with the magnetic field, but for the samples with $m \geqslant 1$ we have observed the opposite effect, i.e. critical temperature increases with the field. In Fig. 2 this is demonstrated for the samples MnBi₂Te₄ and MnBi₁₄Te₂₂.

Fig. 2.

(Color online) Magnetic field dependence of the magnetic transition temperature for the (a) MnBi₂Te₄ and (b) MnBi₁₄Te₂₂ samples. The red dash arrow shows the shift of the maximum with the field.

The most interesting information about the magnetic properties of the samples one can get from the Hall effect measurements, because this effect is determined by the total field ${{H}_{{{\text{tot}}}}} = H + {{H}_{{{\text{int}}}}}$ inside the sample, which is the sum of external applied field H and the internal field ${{H}_{{{\text{int}}}}}$, created by septuple layer blocks, which are 2D magnets. First of all, note, that in MnBi₂Te₄, as in the whole (MnBi₂Te₄) (Bi₂Te₃)_m family, the main carriers are electrons. Electron concentrations and mobilities for our samples are presented in Table 1. One can see from Table 1, that electron concentration is quite high, i.e. the measured transport properties are determined by volume carriers, so the contribution of surface topologically protected states is negligible.

Table 1. Electron concentrations (in cm^–3) and mobilities (in cm²/(V s)) in the measured (MnBi₂Te₄)(Bi₂Te₃)_m family samples obtained from the Hall effect measurements

The Hall effect in MnBi₂Te₄ at different temperatures is presented in Fig. 3a. One can see the sharp step at ${{\mu }_{0}}{{H}_{{SF}}} \approx 4{\kern 1pt}$ T in the dependence of the Hall resistance on the field, which is due to the field-induced spin-flop transition [18]. At $H = {{H}_{{SF}}}$, all septuple layer blocks, having antiparallel spin orientation in small field, abruptly reorient into the canted AFM state [19], in which their out-of-plane magnetization components are parallel to the external field, while the in-plane ones are antiparallel between each other. Above ${{H}_{{SF}}}$, the canted AFM state gradually evolves into the forced FM state [18] and, consequently, the total field ${{H}_{{{\text{tot}}}}}$ increases. When the temperature goes up the step shifts to smaller fields and its sharpness decreases. At $T > {{T}_{N}}$ this effect disappears. Field-induced spin-flop transition can be registered also in the magnetoresistance of the sample, as it is shown in Fig. 3b.

Fig. 3.

(Color online) Field-induced spin-flop transition in MnBi₂Te₄: (a) ${{\rho }_{{xy}}}(H)$ at different temperatures and (b) ${{\rho }_{{xx}}}(H)$ at 5 K.

One can estimate internal field ${{H}_{{{\text{int}}}}}$, created by polarized septuple layer blocks from the step value in ${{\rho }_{{xy}}}(H)$ dependence. At $T = 4.5{\kern 1pt}$ K the field ${{H}_{{{\text{int}}}}}$ at ${{\mu }_{0}}H > 4{\kern 1pt}$ T equals about 1.7 T. Hall effect measurements presented here are in agreement with the results of magnetization and transport measurements for MnBi₂Te₄ ($m = 0)$ [1, 20].

Let us now discuss the $m > 0$ members of the (MnBi₂Te₄)(Bi₂Te₃)_m family. The $m = 1$ compound, MnBi₄Te₇, is known to undergo paramagnet–antiferromagnet phase transition at ${{T}_{N}} \approx 13$ K [6, 15], as evidenced by the temperature-dependent magnetic susceptibility measurements. Remarkably, despite of MnBi₄Te₇ adopting below its ${{T}_{N}}$ exactly the same A‑type AFM state as MnBi₂Te₄, the ${{\rho }_{{xy}}}(H)$ dependencies of these two systems display important differences at low temperatures. This is seen in Fig. 4, which illustrates the Hall effect measured in the MnBi₄Te₇ sample at six different temperatures. First, below ${{T}_{N}}$, the typical signature of an A-type collinear antiferromagnet, i.e., a spin-flop transition, is observed (${{\mu }_{0}}{{H}_{{SF}}} \approx 0.15$ T; see curves measured at 10 and 7 K), similarly to MnBi₂Te₄ (Fig. 3a). However, at lower temperatures, the spin-flop transition starts to show the hysteretic behavior. Finally, at the lowest measurement temperature of 1.4 K there appears a single ${{\rho }_{{xy}}}(H)$ hysteresis curve and a non-zero Hall resistivity in remanence. In [21] this behavior has been interpreted as due to the competition between the interlayer exchange coupling and a temperature-dependent effective anisotropy. The ferromagnetic-like hysteresis loop at low temperature is the signature of a dominant anisotropy energy, which offers the possibility to stabilize remnant fully magnetized (metamagnetic) state. These results of the Hall measurements presented here for MnBi₂Te₇ are in agreement with those reported in the literature [10, 14, 22]. Very similar Hall effect dependences were observed for the $m = 2$ compound, MnBi₆Te₁₀ (not shown).

Fig. 4.

(Color online) Hall effect in MnBi₄Te₇ at different temperatures.

However already at $m \geqslant 3$ the Hall effect in the full temperature range below magnetic transition temperature corresponds to FM state. Indeed, no spin-flop transitions are observed, that would indicate the AFM state, as discussed above. This is seen in Fig. 5a where the set of ${{\rho }_{{xy}}}(H)$ curves at different temperatures for the sample MnBi₁₀Te₁₆ ($m = 4$) are presented. The hysteresis curves in the magnetoresistance for ${{\rho }_{{xx}}}(H)$ of the same sample are shown in Fig. 5b. One can see that this behavior drastically differs from that presented in Figs. 3b and 4 for antiferromagnets with $m = 0$ and 1, respectively. For $m > 4$ we have also observed anomalous Hall effect as well, even in the MnBi₁₄Te₂₂ sample ($m = 6$), and ${{\rho }_{{xy}}}(H)$ curves were similar to those observed for $m = 4$.

Fig. 5.

(Color online) (a) Anomalous Hall effect and (b) magnetoresistance in the MnBi₁₀Te₁₆ sample.

Taking into account that we deal with AFM–FM transition when m increases, the influence of the magnetic field on the transition temperature (see Figs. 2a, 2b and the text) could be explained as follows. When MnBi₂Te₄ above ${{T}_{N}}$ is placed under external magnetic field (Fig. 2a), the latter, along with the temperature, act against the interlayer AFM exchange coupling. As a consequence, when the system approaches ${{T}_{N}}$ from above, the AFM ordering onsets at lower temperatures compared to the case $H = 0$, as seen in Fig. 2a. For $m > 0$, the interlayer exchange coupling strongly weakens as compared to MnBi₂Te₄ [6], but the magnetic anisotropy energy stays roughly the same [23], such that the energy scale of the latter dominates over the former. Therefore, the uniaxial magnetic anisotropy and external magnetic field cooperate to stabilize a FM state at temperatures that are higher than the critical temperature without the field, as seen in Fig. 2b for MnBi₁₄Te₂₂ (the data for MnBi₆Te₁₀ are available in [6]). In this context it is worth noting that already for $m = 1$, i.e., in MnBi₄Te₇, pronounced two-dimensional FM correlations have been detected above critical temperature [23], in spite of the AFM exchange coupling between septuple layers.

Generally speaking, the three-dimensional FM ordering will be lost at high enough $m$ values. Indeed, according to ab initio calculations, performed for $m = 3$ (MnBi₈Te₁₃ and an isostructural hypothetical MnBi₈Sb₁₃), the total energy difference between the interlayer AFM and FM states is negligibly small [24, 25]. Nevertheless, it follows from our measurements that the FM state survives even for $m = 6$ that corresponds to six non-magnetic Bi₂Te₃ layers placed between every two magnetic MnBi₂Te₄ layers in MnBi₁₄Te₂₂. One of the possible explanations of this fact can be condensed to the following. Comparatively high electron concentration of about 10²⁰ cm^–3 in our samples can give rise to Ruderman–Kittel–Kasuya–Yosida (RKKY) interlayer exchange coupling, like in Fe/V superlattices showing non-universal critical behavior and high values of critical index that goes down to its 2D universal value at sufficiently large thicknesses of the vanadium spacer [26]. High value of critical index of 0.4 reported for MnBi₈Sb₁₃ ($m = 3$) [16] cannot be categorized into any universality class and, therefore, favors such assumption. In general, the interlayer RKKY exchange between magnetic layers has an oscillating character, alternately leading to FM and AFM ordering with a positive and negative sign of the exchange constant, respectively. In our case, the interlayer RKKY exchange constant between manganese atoms, estimated using the measured concentration and distance values of Mn–Mn for each m, had a positive sign, which does not contradict the observed FM nature of phase transitions at $m \geqslant 3$. However, it is too early to draw final conclusions. Magnetometric measurements of members of the series with a large m can help clarify the situation.

Alternatively, the observed FM state for $m = 6$ might be a result of the short-range interactions arising due to the Mn–Bi intermixing like in some MnBi₆Sb₁₀ samples that show pure FM behavior at all temperatures below the critical point [27, 28].

In conclusion, the systematic studies of magneto-transport properties of the whole (MnBi₂Te₄)(Bi₂Te₃)_m family of intrinsic magnetic TIs with m = $0,1,...,6$ were carried out for the first time. The crystals with $m = 0$ are A-type antiferromagnets with Neel temperature ${{T}_{N}} = 25.3$ K. The $m = 1$ and 2 compounds (MnBi₄Te₇ and MnBi₆Te₁₀, respectively) are antiferromagnets too, but a significant weakening of the interlayer AFM coupling allows one to stabilize the fully-magnetized metamagnetic state in remanence by gradually reducing the external field strength down to zero. For $m > 2$, the overall behavior changes to FM for all compounds. The magnetic transition in $R(T)$ dependence with critical temperature of 11 K as well as the anomalous Hall effect are observed even for $m = 6$, i.e., when 2D magnets are separated by six non-magnetic quintuple layer blocks. We speculate that for these large separations between Mn layers the RKKY type interlayer exchange coupling may be relevant due to relatively high electron concentrations in the studied samples, although the Mn-Bi intermixing may also provide an alternative interlayer exchange coupling channel. Further research will be required to address the reasons for FM sustainability of ordering at $m \geqslant 3$.