INTRODUCTION

Interest in the study of turbulent flows in a rotating as a whole fluid is due to the wide spectrum of applications, from geophysics and astrophysics to engineering [1, 2]. The technical progress in velocity field flow measurements with the help of particle image velocimetry (PIV) and particle tracking velocimetry (PTV) reached in the last two decades has opened the way for more detailed measurement of structure and dynamics of flow, in particular the turbulent flow in a rotating as a whole fluid (see, e.g., review [3]).

There is a qualitative difference between two-dimensional (2D) and three-dimensional (3D) turbulent statistically isotropic flows. The 3D turbulence is characterized by direct energy cascade [4, 5] whereas the energy cascade is inverse in 2D turbulence [6]. In other words, in the two-dimensional flow, there are vortices merging into larger ones, whereas there is a vortex break-up into smaller ones in the 3D flow. Experiments in 2D turbulence in thin layers [7] showed, that a coherent vortex is generated in a finite system with weak bottom friction at proper conditions. Coherent structures are large-scale, long-lived formations against a small-scale turbulence background [8]. These formations have high universality for a certain turbulent type of motion. Examples of coherent structures are hairpin vortices (horseshoe vortices) in boundary layers [9] and condensates [10].

Generation of coherent vortices is observed in the rotational turbulent flows as well, where the Coriolis force prevails over the inertia force. In this case, columnar vortices are formed that are uniform along the axis of rotation, and the velocity of the flow lies in the plane normal to the axis. So, the effective flow dimension decreases to two, and the direct energy cascade is replaced by the inverse one. Such a quasi-two-dimensional flow has been observed experimentally [11, 12] and in direct numerical simulations [13]. Generally, a turbulent flow in rapidly rotating fluid is a superposition of a quasi-two-dimensional flow and inertial waves [2]. In the main approximation, both flows are independent [14], although they interact due to hydrodynamic nonlinearity [15]. Despite the fact that the coherent vortices have been studied for many years, the mechanisms that determine their structure are not completely understood up to date. The main problem is a closure of the Reynolds equation for the mean flow in the vortex, which is an averaged Navier–Stokes equation over relatively rapid turbulent pulsations. The solution of the closure problem includes the calculation of the Reynolds tensor against the background of the average vortex flow. In the model proposed in [16] and developed in [17], the closure problem is solved in the limit of strong scale separation between the vortex structure and the turbulence pulsations.

The purpose of this letter is to study experimentally the features of the quasi-two-dimensional turbulence in general and, in particular, the time-stable columnar vortices, their radial structure and to determine of the character of the vortices interaction with the inertial waves. We leave beyond the scope of this study the question of how vortices are generated and formed, considering the case of the statistically stationary state.

EXPERIMENTAL METHODOLOGY

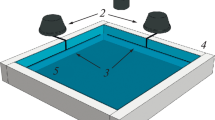
The experimental setup was a cubic glass aquarium with a rib of 1 m mounted on the rotating platform, see Fig. 1a. The cube was completely filled with distilled water and hermetically sealed with a clear glass lid. The visualization of the vortex motion in water was done using the laser sheet methodology. Water was seeded with neutrally buoyant polyamide particles (PA-12) with an average size of 90 μm. The particles were highlighted by the horizontal laser sheet in the middle plane of the cube. The processing of the resulting images by PIV method [18, 19] provided a two-dimensional velocity field in the plane. The excitation of the turbulent motion inside the cube was produced by the rotation of four vertical mixers with 10 blades attached to each, the mixers were located at the corners of the cube, see Fig. 1b. Thus, mixers had non-homogeneous vertical geometry and, as a result, they effectively generated inertial waves. In order for the mixers themselves not to violate the symmetry of the flow, i.e., not to excite its rotation along or against the rotation of the cube, their rotation was periodic: there were two rotations in one direction during first second and two rotations in the opposite direction during 2 s. The mixer rotational velocity was equal in all experimental runs. The symmetry of the mixers motion was tested by the experiment in which the cube rotated in the opposite direction. The obtained results had the same statistical distributions as in the original rotation direction experiments. We note that the methods of the flow forcing closest to ours was used in [20, 21].

Fig. 1.
figure 1

(Color online) (a) Sketch of the experimental setup. (b) Part of the mixer used for the turbulence forcing.

Full size image

All the experiments began with cube unwinding and activation of the forcing at the same time. The experimental runs were carried out for the final rotational speed Ω from 0.12 to 0.72 Hz, that was reached with constant angular acceleration 0.05 Hz/s. The dominant dissipative mechanism for the large-scale quasi-two-dimensional flow component is friction on the cube lid and bottom in the Ekman boundary layer [1, 17]. This friction is characterized by the attenuation time \(\tau = H{\text{/}}(2\sqrt {\nu \Omega } )\), which equals to 600−200 s in our experiments. After starting an experimental run, at least \(5\tau \) is waited for the flow reaches the statistically equilibrium state.

The turbulent macro-Reynolds number [22] \({\text{R}}{{{\text{e}}}_{M}} = {{v}_{{{\text{rms}}}}}{{L}_{f}}{\text{/}}\nu \), calculated from the rms velocity \({{v}_{{{\text{rms}}}}} = {{\langle v_{x}^{2} + v_{y}^{2}\rangle }^{{1/2}}}\) and the blade size \({{L}_{f}} \simeq 6.5\) cm was about 2000 (Fig. 2). The turbulent macro-Rossby number \({\text{R}}{{{\text{o}}}_{M}} = {{v}_{{{\text{rms}}}}}{\text{/}}(2\Omega {{L}_{f}})\) ranged from 0.35 to 0.05, see Fig. 2. The ratio of these parameters \({\text{R}}{{{\text{e}}}_{M}}{\text{/R}}{{{\text{o}}}_{M}}\) is the typical value of the ratio of Coriolis force and bulk viscous force. It is near 5 × 103, that is the standard value for this type of experiments, see review [12]. The values of the dimensionless parameters indicate that the Coriolis force dominates the flow and that the flow itself is moderately turbulent. The observation time in the median horizontal plane was 15 min at a shooting rate of 75 fps. The 2D2C velocity field was obtained from the data using the PIV method [18, 19]. The spatial resolution of the velocity field was 0.4 cm.

Fig. 2.
figure 2

(Color online) (a) (Empty squares) Macro-Reynolds number and (filled circles) the vortex number \(N\) versus the cube rotational speed. (b) (Empty squares) Micro-Rossby number \({\text{R}}{{{\text{o}}}_{\omega }}\) and (filled circles) the macro-Rossby number \({\text{R}}{{{\text{o}}}_{M}}\) versus the cube rotational speed.

Full size image

EXPERIMENTAL RESULTS

Examples of the vorticity field \(\omega = {{\partial }_{x}}{{v}_{y}} - {{\partial }_{y}}{{v}_{x}}\) at half-height horizontal plane are shown in Fig. 3 for the lowest cube rotation frequency 0.12 rot/s (Fig. 3a) and for the highest rotation frequency 0.72 rot/s (Fig. 3b). The yellow color shows the cyclonic rotation (in the direction coinciding with the cube rotation direction) and the blue color shows the anticyclone’s rotation. There are many vortices, mostly cyclones. Vortices are vertically homogeneous, that was tested in a separate experiment where the velocity field was measured in a vertical plane. The vortices move in a horizontal plane with characteristic velocities of several centimeters per second. The anticyclones were weakly marked and had a short lifetime; therefore, we shall speak only about cyclones. The vortex evolution time analysis shows that there exist long-lived vortices with lifetimes exceeding the observation time (900 s). Moreover, there was no significant energy change in the long-lived vortices. Consequently, the vortices exist longer than the Ekman time dissipation.

Fig. 3.
figure 3

(Color online) Vorticity field averaged over 1/3 s at time \(t = 166\) s after the start of the observation at (a) a low rotational speed of 0.12 Hz and (b) a high rotational speed of 0.72 Hz.

Full size image

In Fig. 3a, the number of vortices N is about 2–3 times smaller than in Fig. 3b. The transition from a low number of vortices at low rotational speeds to a high number of vortices at high rotational speeds occurs in a jump-like manner at a rotational speed of about \(\Omega \text{*} \approx 0.35{\kern 1pt} \) rot/s, see Fig. 2a, rather than linearly as it is observed in [23]. The number of vortices varied weakly during one experiment. Despite the fact that vortex number rapidly changed with cube rotational speed, some other parameters did not show similar behavior among which are micro-Rossby number \({\text{R}}{{{\text{o}}}_{\omega }}\), calculated as mean vorticity in the cyclone’s core divided by \(2\Omega \), and macro-Rossby number \({\text{R}}{{{\text{o}}}_{M}}\) (Fig. 2b). Notably, there is almost linear dependence \({\text{R}}{{{\text{o}}}_{\omega }} = 3.5{\text{R}}{{{\text{o}}}_{M}} + 0.3\). This plot shows that vortices are relatively stronger at low-frequency cube rotation. The plot of the macro-Reynolds number \({\text{R}}{{{\text{e}}}_{M}}\) (Fig. 2a) also does not show any features near the frequency \(\Omega {\text{*}}\).

The jump dependence of the vortices number N, nevertheless, is consistent with the jump dependence of the more complete flow statistical information. The probability density function (PDF) for the local Rossby number \({\text{Ro}}(\mathbf{r}) = \omega (\mathbf{r}){\text{/}}2\Omega \) plotted at different cube rotational speeds with \(\mathbf{r} = \{ x,y\} \) in Fig. 4 for a region not including boundary layers also shows a jump-like change. At low speeds, this number within anticyclones satisfies the inequality \({\text{Ro}}(\mathbf{r}) > - 1\). At high speeds, the lower bound is \({\text{Ro}}(\mathbf{r}) > - 0.5\). The upper bound of the distribution is similarly narrowed at high speeds. It should be noted, however, that the jump in the shape of the PDF tails occurs at a lower rotational speed than the jump in the number of vortices N. In general, despite that the other method of turbulence excitation was used here, the PDFs are similar to those obtained by earlier researchers in [22, 24]. In particular, the distributions are not symmetric with respect to zero and correspond to intermittent statistics. In our experiment, the skewness was 1.33 and 2.4 at the lowest and highest speeds, respectively. Note here that precisely because the Rossby number reaches values of the order of one, we do not use the term “geostrophic” as a characterization of the quasi-two-dimensional flow in general and the columnar vortices in particular [2, 15], although this distinction becomes conditional when the inequality \({\text{Ro}}(\mathbf{r}) > - 1\) is satisfied.

Fig. 4.
figure 4

(Color online) Probability density function of the local Rossby number \({\text{Ro}}(\mathbf{r}) = \omega {\text{/}}2\Omega \).

Full size image

Based on these observations, we can suggest the existence of two essentially different turbulent regimes of quasi-two-dimensional flow. Let us consider in details the properties of column vortices in these two regimes.

Low Cube Rotation Speed

To measure the statistical properties of a single vortex, it is necessary to move to the reference frame which origin is places on its axis. Following [10], the position of the vortex center in the first approximation is determined as coinciding with the vorticity extremum point. Thereafter, we implemented the position clarification procedure as follows: inside a 5 cm square region centered at the vorticity extremum point, the position of the vortex center was defined as the point corresponding to the maximum of velocity field circulation, that was calculated on the circle centered at the point and with radius of 2.5 cm.

The radial profile of the azimuth velocity component in vortex \(U_{G}^{\varphi }(r) = {{\langle U_{i}^{\varphi }(r,\varphi ,t)\rangle }_{{\varphi ,t,i}}}\) was plotted for each rotational speed where the averaging was performed over the angle φ, time t and number i of the traced vortex, see Fig. 5a, where r is distance to the vortex axis. At interval from 2 to 20 cm, \(U_{G}^{\varphi }(r)\) remains almost constant. The similar flat radial profile was obtained experimentally [25] in the conductive fluid thin layer with the electromagnet forcing type. Also, the velocity circulation radial derivative dependence \(\Gamma {\kern 1pt} '(r) = r{{\langle {{\omega }_{i}}(r,\varphi ,t)\rangle }_{{\varphi ,t,i}}}\) was plotted (blue dash-dotted curve in the Fig. 5a). It should be noted that \(\Gamma {\kern 1pt} '(r)\) profile has not sign change. The vortex core radius \({{r}_{{{\text{core}}}}}\) which has been defined according to the equation \({{r}_{{{\text{core}}}}}{{\omega }_{G}}{{{\text{|}}}_{{r = 0}}} = 2U_{G}^{\varphi }({{r}_{{{\text{core}}}}})\) was about 2.3 cm.

Fig. 5.
figure 5

(Color online) (Solid line) Azimuth vortex velocity profiles \(U_{G}^{\varphi }(r)\), (dash-dotted line) values of \(\Gamma {\kern 1pt} '(r)\), (blue dashed straight line) value of the approximation of the mean current velocity profile \({{U}^{\varphi }}(r) = \bar {\omega }r{\text{/}}2\), (black dashed line) azimuthal velocity profile with subtracted mean current velocity profile \(U_{G}^{\varphi }(r) - {{U}^{\varphi }}(r)\) at (a) a low rotational speed of 0.12 rps (\(\bar {\omega } = 0.06{\kern 1pt} \) s−1) and (b) a high rotational speed of 0.72 rps (\(\bar {\omega } = 0.047\) s−1).

Full size image

The relatively large number of vortices makes it meaningful to consider the global mean flow on the scale of the entire flow region. In order to separate the flow associated with the vortex under consideration from the global mean flow, we subtracted from the measured velocity profile \(U_{G}^{\varphi }(r)\) the velocity of the global mean current \({{U}^{\varphi }}(r)\). Based on the observation of in average uniform filling of the available flow region with vortices, we approximated \({{U}^{\varphi }}(r)\) by a linear velocity profile, \({{U}^{\varphi }}(r) = \bar {\omega }r{\text{/}}2\). To determine the mean vorticity \(\bar {\omega }\) outside the boundary layer, we performed linear approximation for the velocity \(U_{G}^{\varphi }(r)\) at distances greater than 30 cm (green dashed line in Fig. 5). Subtracting the collective rotation of the vortices from the previously calculated azimuth velocity profile \(U_{G}^{\varphi }(r)\) allows us to empirically determine the radius of the vortices as the point where \(U_{G}^{\varphi }(r) - {{U}^{\varphi }}(r)\) turns to zero (see Fig. 5). The radius of the vortices calculated in this way is \( \simeq {\kern 1pt} 25\) cm. Note that the mean flow velocity \(\langle U\rangle \), calculated by averaging the velocity field over the entire experiment time, matches with good accuracy the same estimate \(\bar {\omega }{\kern 1pt} {\kern 1pt} r{\text{/}}2\), where r is the distance to the cube center in this case.

High Cube Rotation Speed

Radial profiles of the azimuth velocity \(U_{G}^{\varphi }(r)\) and of \(\Gamma {\kern 1pt} '(r)\) are shown in Fig. 5b. The vortices were largely isolated (in terms of [26]). In isolated vortices, the vorticity inside the core region of the vortex is compensated by the vorticity of the opposite sign inside the body of the vortex, so that the total circulation \(\Gamma (r)\) associated with the vortex (integral of \(\Gamma {\kern 1pt} '(r)\)) is zero. In our case, \(\Gamma (r)\) reached its minimum at \( \simeq {\kern 1pt} 15\) cm, which can be considered as the radius of these vortices. The radius of the vortex core \({{r}_{{{\text{core}}}}}\) was the same 2.3 cm. The linear approximation of the mean flow \(\langle U\rangle \) is still well described by the coefficient \(\bar {\omega }\).

Thus, at high rotational speed, the vortices appear not only relatively weaker, but also smaller, that, of course, is in agreement with their larger number per unit area. An integral measure of both vortex strength and its magnitude can serve the magnitude of fluctuations of the flow energy against the background of the average \(\langle U\rangle \). In Fig. 6 we plot the dependences of the mean energy density of the full flow \(v_{{{\text{rms}}}}^{{\text{2}}}{\text{/}}2\) and the energy density of the mean flow \({{\langle U\rangle }^{2}}{\text{/}}2\) on the rotational speed. Subtracting the latter from the former, we obtain the measure sought—the kinetic energy contained in the individual vortices. According to Fig. 6, it does not depend on the rotation frequency of the cube. Note that this quantity is relatively stable with respect to the counting method. For example, if we counted the vortex energies by integrating the compensated profile squared \({{(U_{G}^{\varphi }(r) - {{U}^{\varphi }}(r))}^{2}}\), see Fig. 5, then the ratio of the energy of isolated vortices to vortices at low cube rotational speed would be 0.5−0.6. The quantity being multiplied by the number of the vortices is proportional to the mean energy contained in the individual vortices per unit area and is almost independent of the rotational speed as well. As a result, if we now normalize the energy of the vortices by \({{\Omega }^{2}}\), we again conclude that the vortices at high rotational speeds are relatively weaker.

Fig. 6.
figure 6

(Color online) (Empty circles) Mean energy, (asterisks \( * \)) the mean stream energy, and (filled circles) the difference between the total energy and the mean stream energy versus the cube rotational speed.

Full size image

DISCUSSION

The coherent vortices were observed in turbulent flow inside the rotating cube. Their lifetimes was much longer than the Ekman time. Two mechanisms for maintaining the energy of the vortices can be suggested. The first one is the columnar vortex merging mechanism, when a newly separated vortex from a mixer merges with another vortex already presented in the volume [27]. The second energy-maintaining mechanism is inertial wave absorption, that requires the fulfillment of conditions \({\text{R}}{{{\text{e}}}_{M}} \gg 1\) and \({\text{Ro}}(\mathbf{r}) \succcurlyeq - 1\) [22, 28, 29].

The second mechanism can be suppressed if the macro-Rossby number \({\text{R}}{{{\text{o}}}_{M}}\) is less than some threshold value. Let us show this by assuming the Rossby number to be small, \({\text{Ro}}(\mathbf{r}) \ll 1\). Neglecting the nonlinear interaction between inertial waves and assuming the wave length is smaller than the quasi-two-dimensional characteristic flow scale, we can describe the nonlinear influence of the inhomogeneity of the quasi-two-dimensional flow \({{U}_{\alpha }}(t,\mathbf{r})\) on the wave evolution with perturbation theory. The wave is described by the velocity field \(\mathbf{u}(t,\mathbf{r},z)\). Consider a wave packet that moves along a trajectory \(\mathbf{R}(t)\). We linearize the Navier–Stokes equation with respect to u and write it in Fourier space in the vicinity of the point R:

$$\begin{gathered} \left( {{{\partial }_{t}} + i(\mathbf{U}(t,\mathbf{R}) \cdot \mathbf{k}) - {{\sigma }_{{\beta \alpha }}}{{k}_{\beta }}\frac{\partial }{{\partial {{k}_{\alpha }}}}} \right)\mathbf{u} + 2[\mathbf{\Omega} \times \mathbf{u}] \\ = - {\kern 1pt} {{((\mathbf{u} \cdot \nabla )\mathbf{U})}_{\mathbf{k}}} - i\mathbf{k}p - \nu {{k}^{2}}\mathbf{u}, \\ \end{gathered} $$
(1)

where k is a wave vector, the velocity gradient of the quasi-two-dimensional flow \({{\sigma }_{{\beta \alpha }}}(t) = {{\partial }_{\alpha }}{{U}_{\beta }}(t,\mathbf{R})\) is taken at the location \(\mathbf{R}(t)\) of the wave packet and the indices \(\alpha ,\beta = \{ x,y\} \). Because of the relative smallness of the wavelength, it is sufficient to approximate the quasi-two-dimensional velocity field by a linear profile.

Let’s analyze Eq. (1). The second summand in the parenthesis in the left-hand side provides the wave packet advection with the flow velocity \(\mathbf{U}(t,\mathbf{R}(t))\). Let the wave packet has the wave vector K. Coriolis force in (1) leads to the wave packet motion relative to the fluid with the group velocity, which horizontal components are \(V_{\alpha }^{g} = (2\Omega {{K}_{z}}{\text{/}}{{K}^{3}}){{K}_{\alpha }}\). The horizontal components of the wave packet velocity are therefore

$$\frac{{{\text{d}}{{R}_{\alpha }}}}{{{\text{d}}t}} = V_{\alpha }^{g}(t) + {{U}_{\alpha }}(t,\mathbf{R}).$$
(2)

The third summand in the parenthesis of the left-hand side expresses the influence of the flow inhomogeneity on the wave field. Its effect on any field, including the field of the inertial wave, leads to the change of the wave vector K along the characteristics [16, 17],

$${\text{d}}{{K}_{\alpha }}{\text{/d}}t = - {{\sigma }_{{\beta \alpha }}}{{K}_{\beta }},\quad {{K}_{z}} = {\text{const}}.$$
(3)

Note that the same summand together with the summands in the right-hand side provide the variation of the wave amplitude with time.

Now consider an axially symmetric columnar vortex with a velocity field \({{U}_{\alpha }} = U_{G}^{\varphi }(r)e_{\alpha }^{\varphi }\), where the vector r starts from the vortex axis and the unit vector \(e_{\alpha }^{\varphi }\) is directed along the azimuth. The gradient of the field is

$${{\sigma }_{{\beta \alpha }}} = \Sigma {{r}_{\alpha }}e_{\beta }^{\varphi }{\text{/}}r + (U_{G}^{\varphi }{\text{/}}r){{\epsilon }_{{\beta \alpha }}},$$
(4)

where the local shear rate is \(\Sigma = r{{\partial }_{r}}(U_{G}^{\varphi }{\text{/}}r)\) and \({{\epsilon }_{{\alpha \beta }}}\) is the unit antisymmetric tensor of the second rank, \({{\epsilon }_{{xy}}} = 1\). The second summand in (2) produces the advection of the wave packet together with fluid volume element moving along a circular orbit inside the vortex, and the second summand in (4) produces the rotation of the wave vector together with the element according to (3). Both of these contributions can be eliminated by changing to the coordinate system associated with the element. In the coordinate system, the system of Eqs. (3) and (2) takes the form

$$\frac{{{\text{d}}{{K}_{r}}}}{{{\text{d}}t}} = - \Sigma {{K}_{\varphi }},\quad \frac{{{\text{d}}R}}{{{\text{d}}t}} = V_{r}^{g} = \frac{{2\Omega {{K}_{z}}{{K}_{r}}}}{{{{k}^{3}}}},$$
(5)

and the components \({{K}_{z}}\) and \({{K}_{\varphi }}\) do not change with time. Excluding time from the system of Eqs. (5), we obtain

$$\frac{{{{K}_{z}}}}{{{{K}_{\varphi }}}}{\text{d}}\left( {\frac{1}{K}} \right) = \frac{1}{{2\Omega }}\Sigma {\kern 1pt} {\text{d}}R.$$
(6)

As it should be for a non-dissipative system, the wave parameter change process is reversible. The irreversibility can be obtained in the case when the integral of the right-hand side of Eq. (6) turns out to be so large in absolute value at some moment that the absolute value K of the wave vector goes to infinity. Taking into account the viscosity, this means that the wave disappears and its energy is transferred to the quasi-two-dimensional flow. Since the integral of the right-hand side of Eq. (4) and the value of the wavenumber far from the vortex are estimated as \({{v}_{{{\text{rms}}}}}{\text{/}}2\Omega \) and \(K \sim 1{\text{/}}{{L}_{f}}\) respectively, the irreversibility is achieved if the macro-Rossby number exceeds some threshold value, \({\text{R}}{{{\text{o}}}_{M}} > {\text{Ro}}_{M}^{*}\). The above requirement that the local Rossby number be small means \(\Sigma {\text{/}}2\Omega \ll 1\), otherwise one should take into account corrections to the rotation frequency Ω from the current [26]. However, the conclusions drawn remain qualitatively correct even if this condition is violated.

The threshold macro-Rossby number \({\text{Ro}}_{M}^{*} \approx 0.1\) according to Fig. 3b. At the rotational speeds less than Ω*, we can count on the applicability of the theory developed in [10, 16, 17]. Indeed, there is a radius range where the mean velocity remains almost constant \(U_{G}^{\varphi }(r)\), see Fig. 5a, that is in accordance with the theoretical estimates presented in [17]. The theory developed in this letter predicts that harmonics with large wavenumber are formed in this region during wave absorption, that is in agreement with experimental data: the energy spectrum behaves as \({{k}^{{ - 2.4}}}\) at low rotational speeds, while the index decreases down to \( \simeq - 3.3\) at high rotational speeds. However, our attempts, following [30], to establish the validity of the Reynolds equation in vortex showed that the total observation time does not provide enough data for sufficient statistical averaging of the Reynolds tensor.

CONCLUSIONS

Two turbulent regimes for the quasi-two-dimensional flow in rotating fluid were experimentally observed in the vessel with the horizontal boundaries. The regimes have different numbers of cyclones and their profiles. In both regimes, the cyclones are time-stable structures that live much longer than the viscous dissipation time. The switching between regimes occurs at the threshold macro-Rossby number \({\text{Ro}}_{M}^{*} \approx 0.1\), which is the ratio of the flow velocity amplitude and inertial waves group velocity. We presented theoretical arguments in favor of the fact that the transition is accompanied by a change in the mode of interaction of inertial waves with quasi-two-dimensional flow. At relatively low vessel rotational speeds, which correspond to relatively large number \({\text{R}}{{{\text{o}}}_{M}} > {\text{Ro}}_{M}^{*}\), the quasi-two-dimensional flow efficiently absorbs inertial waves. At relatively high rotational speeds, the number drops, so that the efficiency of energy transfer from the inertial waves to the columnar vortices decreases.