INTRODUCTION

Magnetic skyrmions are topologically nontrivial whirls of local magnetization. They may serve as building blocks for novel racetrack memory devices [1] or programmable logic devices [2], thanks to topological protection, small size and ability to be manipulated by spin torques.

One can consider a magnetic skyrmion [3] as an extremely small magnetic bubble [4] (cylindrical domain wall [5]). In terms of domain walls, skyrmion radius is comparable with its width and defined by Dzyaloshinskii–Moriya interaction (DMI) constant [3, 6].

The dynamics of a local magnetization is usually described by the Landau–Lifshitz–Gilbert (LLG) equation. LLG equation can be further transformed into the Thiele [7] equation in case of domain wall steady motion. Thiele equation and its generalizations [8] are the main tool for skyrmions motion analysis [9]. Thiele equation allows one to take into account the spin current impact on skyrmions and discuss the situation of skyrmions on a track, see [9].

In non-centrosymmetric magnets with DMI magnetic skyrmions are often arranged into regular lattices [10–12]. Such lattices (called also skyrmion crystals (SkX) [13]) are preferable to uniform, helix or cone configurations in case when a single skyrmion configuration becomes energetically more favorable [14]. It was shown that the densely packed skyrmion configurations is characterized by both pairwise repulsive and triple attractive interaction between skyrmions [15]. Hence, the motion of individual skyrmions in a lattice depends on its neighbors, and the SkX dynamics cannot generally be reduced to the motion of solitary skyrmion in a potential well.

Excitations of SkX have are described by the complicated band structure [16–19]. The lattice excitations of different angular symmetry correspond to different distortions of individual skyrmions, among them elliptical deformation, breathing mode, clockwise and counter-clockwise motion, etc. The modes with certain symmetries [20] show up in magnetic resonance experiments [21].

The soft Goldstone mode of SkX, also called gyrotropic mode, is associated with displacement of skyrmions in SkX and was predicted in [22]. SkX was represented there as a sum of three magnetic helices with the corresponding phase shifts, and it was shown that the topological term in the Lagrangian leads to quadratic dispersion of the soft mode (it was recently verified numerically in [23]). The gyrotropic mode does not manifest itself in magnetic resonance experiments [24], but somehow appears in inelastic neutron scattering [25].

In this work we consider a simplest model of non-centrosymmetric ferromagnet with DMI in external magnetic field, whose ground state is SkX in a certain range of parameters. Staying in a framework of stereographic projection approach and regarding skyrmions in quasiparticles paradigm, we consider a displacement field of skyrmions positions in the lattice. We numerically show the nearest-neighbor character of displacements’ coupling and obtain closed form of dispersion of the Goldstone mode. The dependence of force constants on external magnetic field is also numerically found. The dynamic Green’s function of displacements is isotropic at small distances, while showing anisotropic tensor structure at larger distances.

MODEL

We consider planar model of non-centrosymmetric ferromagnet with DMI in uniform external magnetic field perpendicular to the plane. The energy density is given by:

$$\mathcal{E} = \frac{C}{2}{{\partial }_{\mu }}{{S}_{i}}{{\partial }_{\mu }}{{S}_{i}} - D{{\epsilon }_{{\mu ij}}}{{S}_{i}}{{\partial }_{\mu }}{{S}_{j}} - B{{S}_{3}},$$
(1)

where C is an exchange parameter, D is DMI constant, and B is an external magnetic field magnitude. There is a convenient way to choose measurement units in the model (1): we will measure length in the units of \(l = C{\text{/}}D\), and energy density in the units of \(C{{S}^{2}}{{l}^{{ - 2}}} = {{S}^{2}}{{D}^{2}}{\text{/}}C\). Then the energy of the model depends only on the dimensionless parameter \(b = BC{\text{/}}S{{D}^{2}}\). We consider low temperature limit, when local magnetization is saturated, and its magnitude does not change from point to point \({\mathbf{S}} = S{\mathbf{n}}\), with \({\text{|}}{\mathbf{n}}{\text{|}} = 1\). The above planar model is applicable also to thin films, whose thickness is less or comparable to l. We ignore the magnetic dipolar interaction here, because it can be reduced to uniaxial anisotropy for ultrathin films. Small anisotropy leads only to minor changes of SkX parameters.

The stereographic projection representation of the vector n reads as

$${{n}_{1}} + i{{n}_{2}} = \frac{{2f}}{{1 + f\bar {f}}}{\kern 1pt} ,\quad {{n}_{3}} = \frac{{1 - f\bar {f}}}{{1 + f\bar {f}}},$$
(2)

with f a complex-valued function, and \(\bar {f}\) its complex conjugate. A single skyrmion stereographic function is conveniently represented by

$${{f}_{1}} = \frac{{i{\kern 1pt} {{z}_{0}}{\kern 1pt} \kappa (z\bar {z}{\text{/}}z_{0}^{2})}}{{\bar {z}}},$$
(3)

where κ is a smooth real profile function, \({{z}_{0}}\) is a skyrmion size parameter. The ansatz (3) is more convenient for the description of SkX case, while in case of one skyrmion it reproduces the profile obtained by usual bubble domain ansatz. It was shown previously that the multi-skyrmion configurations can be built as a sum of stereographic functions of individual skyrmions [15]. Particularly, the regularly arranged SkX corresponds to the following stereographic function:

$${{f}_{{SkX}}} = \sum\limits_{n,m} {{f}_{1}}({\mathbf{r}} - n{{{\mathbf{a}}}_{1}} - m{{{\mathbf{a}}}_{2}}),$$
(4)

where \({{{\mathbf{a}}}_{1}} = (0,a)\), \({{{\mathbf{a}}}_{2}} = ( - \sqrt 3 a{\text{/}}2,a{\text{/}}2)\), and \(a\) is a cell parameter of SkX see Fig. 1. The static properties of this ansatz given by Eqs. (3) and (4) was discussed to some detail in previous works [14, 15]. It was shown that the proposed SkX configuration has lower energy than helix or unifo-rm configuration at magnetic fields, \(0.25 \lesssim b \lesssim 0.8\).

Fig. 1.
figure 1

(Color online) Sketch of SkX with one displaced skyrmion. Red arrows and a hexagon illustrate lattice vectors and the primitive cell of SkX, the orange circle shows a typical value of z0 parameter, green arrow indicates a displacement of skyrmion in the right top corner. The Brillouin zone with symmetry points is depicted in the bottom right corner.

Full size image

The dynamics of local magnetization follows from the Lagrangian, \(\mathcal{L} = \mathcal{T} - \mathcal{E}\), with the kinetic term

$$\mathcal{T} = \frac{S}{{{{\gamma }_{0}}}}(1 - \cos \theta )\dot {\varphi }{\kern 1pt} ,$$
(5)

here φ and θ define the magnetization direction \({\mathbf{n}} = (\cos \varphi \sin \theta ,\sin \varphi \sin \theta ,\cos \theta )\), and \({{\gamma }_{0}}\) gyromagnetic ratio. This form of the Lagrangian leads to the well-known Landau–Lifshitz equation. The expression (5) may be rewritten in terms of f as

$$\mathcal{T}[f] = \frac{i}{2}\frac{{\bar {f}{{\partial }_{t}}f - f{{\partial }_{t}}\bar {f}}}{{1 + f\bar {f}}}{\kern 1pt} ,$$
(6)

and the factor \(S{\text{/}}{{\gamma }_{0}}\) was included into the time scale. The exact equation of motion for \(f(t)\) is highly nonlinear and cannot generally be solved. In previous works [19, 20] we have discussed the normal modes of infinitesimal fluctuations of the function f. In this work we develop a special approach for consideration of the gyrotropic mode of SkX.

DISPLACEMENT FIELD AND DISPERSION

In our previous papers we associated the above configuration \({{f}_{{SkX}}}\), Eq. (4), with the equilibrium spin configuration, \({{f}_{0}}\), and considered small fluctuations, \(\delta f\), around it, writing

$$f = {{f}_{0}} + \delta f \equiv {{f}_{0}} + (1 + {{f}_{0}}{{\bar {f}}_{0}})\psi {\kern 1pt} ,$$

with the dynamics of ψ is discussed at length in [19].

In this study we assume that the skyrmion lattice is imperfect, in the sense that the stereographic image is still given by the sum of individual images of skyrmions, and the shape of each image is unchanged, but the only imperfection is the position of the center of skyrmions. It is similar to the description of ions’ displacements in crystals in the theory of phonons.

$${{f}_{{SkX}}} = \sum\limits_l {{f}_{1}}({\mathbf{r}} - {\mathbf{r}}_{l}^{{(0)}} + {{{\mathbf{u}}}_{l}}),$$
(7)

where \({\mathbf{r}}_{l}^{{(0)}} = n{{{\mathbf{a}}}_{1}} + m{{{\mathbf{a}}}_{2}}\) with integer \(n,m\) and \({{{\mathbf{a}}}_{{1,2}}}\) lattice vectors. For infinitesimal displacements \({{{\mathbf{u}}}_{l}}\) we can write

$${{f}_{{SkX}}} \simeq {{f}_{0}} + \sum\limits_l {{{\mathbf{u}}}_{l}}\nabla {{f}_{1}}({\mathbf{r}} - {\mathbf{r}}_{l}^{{(0)}}).$$
(8)

In order to make use of our previously found formulas in [19], we define the quantity \(\psi ({\mathbf{r}})\) as

$$\sum\limits_l {{{\mathbf{u}}}_{l}}\nabla {{f}_{1}}({\mathbf{r}} - {\mathbf{r}}_{l}^{{(0)}}) = (1 + {{f}_{0}}{{\bar {f}}_{0}}){\kern 1pt} \psi ({\mathbf{r}}),$$
(9)

also \({{{\mathbf{u}}}_{j}}\nabla = u_{j}^{ + }{{\partial }_{z}} + u_{j}^{ - }{{\partial }_{{\bar {z}}}}\) with \({{\partial }_{z}} = ({{\partial }_{x}} - i{{\partial }_{y}}){\text{/}}2\), \({{\partial }_{{\bar {z}}}} = ({{\partial }_{x}} + i{{\partial }_{y}}){\text{/}}2\) and \(u_{j}^{ \pm } = u_{j}^{x} \pm iu_{j}^{y}\). Introducing shorthand notation \({{f}_{j}} = {{f}_{1}}({\mathbf{r}} - {\mathbf{r}}_{j}^{{(0)}})\) we can write

$$\psi = \sum\limits_j \frac{{u_{j}^{ + }{{\partial }_{z}}{{f}_{j}} + u_{j}^{ - }{{\partial }_{{\bar {z}}}}{{f}_{j}}}}{{1 + {{f}_{0}}{{{\bar {f}}}_{0}}}},$$
(10)

and similarly for complex conjugated \(\bar {\psi }\). As a result, we obtain

$$\begin{gathered} \left( {\begin{array}{*{20}{c}} \psi \\ {\bar {\psi }} \end{array}} \right) = \frac{1}{{1 + {{f}_{0}}{{{\bar {f}}}_{0}}}}\sum\limits_j \left( {\begin{array}{*{20}{c}} {{{\partial }_{{\bar {z}}}}{{f}_{j}},}&{{{\partial }_{z}}{{f}_{j}}} \\ {{{\partial }_{{\bar {z}}}}{{{\bar {f}}}_{j}},}&{{{\partial }_{z}}{{{\bar {f}}}_{j}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {u_{j}^{ - }} \\ {u_{j}^{ + }} \end{array}} \right){\kern 1pt} \\ \equiv \sum\limits_j {{\mathcal{O}}_{j}}\left( {\begin{array}{*{20}{c}} {u_{j}^{ - }} \\ {u_{j}^{ + }} \end{array}} \right){\kern 1pt} . \\ \end{gathered} $$
(11)

For the uniform shift \({{{\mathbf{u}}}_{j}} = {\mathbf{u}}\), using the property \(\sum\nolimits_j ({{f}_{j}},{{\bar {f}}_{j}}) = ({{f}_{0}},{{\bar {f}}_{0}})\), we restore the previously discussed zero modes (Eqs. (29) in [19]):

$$\begin{gathered} {{\Psi }_{\oslash}} = \frac{1}{{1 + {{f}_{0}}{{{\bar {f}}}_{0}}}}\left( {\begin{array}{*{20}{c}} {{{\partial }_{{\bar {z}}}}{{f}_{0}}} \\ {{{\partial }_{{\bar {z}}}}{{{\bar {f}}}_{0}}} \end{array}} \right){\kern 1pt} , \\ {{{\bar {\Psi }}}_{{\oslash}}} = {{\sigma }_{1}}\Psi _{\oslash}^{*} = \frac{1}{{1 + {{f}_{0}}{{{\bar {f}}}_{0}}}}\left( {\begin{array}{*{20}{c}} {{{\partial }_{z}}{{f}_{0}}} \\ {{{\partial }_{z}}{{{\bar {f}}}_{0}}} \end{array}} \right){\kern 1pt} . \\ \end{gathered} $$
(12)

The quadratic in displacements part of the Lagrangian takes the form

$$\mathcal{L} = \frac{1}{2}\sum\limits_{lj} \left( {\begin{array}{*{20}{c}} {u_{l}^{ + },}&{u_{l}^{ - }} \end{array}} \right)\left( { - i{{{\hat {\mathcal{K}}}}_{{lj}}}{{\partial }_{t}} - {{{\hat {\mathcal{H}}}}_{{lj}}}} \right)\left( {\begin{array}{*{20}{c}} {u_{j}^{ - }} \\ {u_{j}^{ + }} \end{array}} \right){\kern 1pt} ,$$
$${{\hat {\mathcal{K}}}_{{lj}}} = \int d{\mathbf{r}}{\kern 1pt} \mathcal{O}_{l}^{\dag }{{\sigma }_{3}}{{\mathcal{O}}_{j}},$$
(13)
$${{\hat {\mathcal{H}}}_{{lj}}} = \int d{\mathbf{r}}\mathcal{O}_{l}^{\dag }\left( {\begin{array}{*{20}{c}} {{{{( - i\nabla + {\mathbf{A}})}}^{2}} + U}&V \\ {V{\text{*}}}&{{{{(i\nabla + {\mathbf{A}})}}^{2}} + U} \end{array}} \right){{\mathcal{O}}_{j}},$$

with the explicit form of U, V and A is given in [19].Footnote 1

Let us discuss a few general properties.

(i) Due to translation invariance, the quantities \({{\hat {\mathcal{K}}}_{{lj}}}\) and \({{\hat {\mathcal{H}}}_{{lj}}}\) depend only on the difference \({\mathbf{d}} = {\mathbf{r}}_{l}^{{(0)}} - {\mathbf{r}}_{j}^{{(0)}}\).

(ii) The zero mode corresponds to summation over j, and we should have \(\sum\nolimits_j {{\hat {\mathcal{H}}}_{{lj}}} = \sum\nolimits_l {{\hat {\mathcal{H}}}_{{lj}}}\) = 0, see below.

(iii) The image of a single skyrmion \({{f}_{1}}({\mathbf{r}})\) decreases exponentially with distance. It follows that \({{\hat {\mathcal{K}}}_{{lj}}}\), \({{\hat {\mathcal{H}}}_{{lj}}}\) decrease rapidly with \({\text{|}}{\mathbf{r}}_{l}^{{(0)}} - {\mathbf{r}}_{j}^{{(0)}}{\text{|}}\). For practical reasons it suffices to consider only on-site term, \(l = j\), and the nearest neighbors (NN).

(iv) It can be shown that \(\sum\nolimits_j {{\hat {\mathcal{K}}}_{{lj}}} = \pi {{\sigma }_{3}}\), it corresponds to the value of topological charge per unit cell of skyrmion crystal.

(v) For triangular lattice with six NN we have \({\mathbf{d}} = (a{\kern 1pt} \cos {{\phi }_{d}},a{\kern 1pt} \sin {{\phi }_{d}})\) with \({{\phi }_{d}} = \frac{\pi }{3}(n - 1{\text{/}}2)\) and \(n = 0, \ldots ,5\). Individual skyrmions are characterized by certain chirality, \({{f}_{1}}({\mathbf{r}}) \propto {{e}^{{i\phi }}}{\text{/}}r\). Considering the symmetry of the potentials \(U,V\) and matrix \({{\mathcal{O}}_{j}}\) under the rotation \(\phi \to \phi + {{\phi }_{d}}\), we notice that the phase \({{\phi }_{d}}\) doubles in the off-diagonal components and is absent in diagonal components of \({{\hat {\mathcal{H}}}_{{lj}}}\). As a result, we have a structure

$${{\hat {\mathcal{H}}}_{{lj}}} = \left( {\begin{array}{*{20}{c}} {{{h}_{1}},}&{{{h}_{2}}{{e}^{{ - 2i{{\phi }_{d}}}}}} \\ {{{h}_{2}}{{e}^{{2i{{\phi }_{d}}}}},}&{{{h}_{1}}} \end{array}} \right){\kern 1pt} ,$$

with \({{h}_{{1,2}}}\) depending only on the distance, d. For the on-site term \(l = j\), the off-diagonal components are absent, \({{h}_{2}} = 0\). Numerically, we find that \({{h}_{{1,2}}} < 0\) for \(l \ne j\).

(vi) The Thiele equation for the motion of the lth skyrmion is obtained by putting \(u_{j}^{ \pm } = 0\) in (13) for all \(j \ne l\). In this case the Lagrangian becomes \({{\mathcal{K}}_{{ll}}}u_{l}^{x}\dot {u}_{l}^{y} - {{h}_{1}}((u_{l}^{x}{{)}^{2}} + {{(u_{l}^{y})}^{2}})\), cf. [26]. Notice that even if \(u_{j}^{ \pm } = 0\) initially, the collective character of Eq. (13) leads to eventual propagation of perturbation around the initial displacement. We discuss it in more detail below.

Using the above properties, we represent the quadratic part of the Lagrangian as

$$\mathcal{L} = \frac{1}{2}\sum\limits_{\mathbf{q}} \left( {\begin{array}{*{20}{c}} {u_{{ - {\mathbf{q}}}}^{ + },}&{u_{{ - {\mathbf{q}}}}^{ - }} \end{array}} \right)\left( { - i{{{\hat {\mathcal{K}}}}_{{\mathbf{q}}}}{{\partial }_{t}} - {{{\hat {\mathcal{H}}}}_{{\mathbf{q}}}}} \right)\left( {\begin{array}{*{20}{c}} {u_{{\mathbf{q}}}^{ - }} \\ {u_{{\mathbf{q}}}^{ + }} \end{array}} \right),$$
$${{\hat {\mathcal{K}}}_{{\mathbf{q}}}} = (\pi + {{k}_{1}}{{\gamma }_{s}}({\mathbf{q}})){{\sigma }_{3}},$$
(14)
$${{\hat {\mathcal{H}}}_{{\mathbf{q}}}} = \left( {\begin{array}{*{20}{c}} {{{h}_{1}}{{\gamma }_{s}}({\mathbf{q}}),}&{{{h}_{2}}{\kern 1pt} \gamma _{d}^{*}({\mathbf{q}})} \\ {{{h}_{2}}{\kern 1pt} {{\gamma }_{d}}({\mathbf{q}}),}&{{{h}_{1}}{{\gamma }_{s}}({\mathbf{q}})} \end{array}} \right),$$

where we defined \(u_{j}^{x} \pm iu_{j}^{y} = \sum\nolimits_{\mathbf{q}} {{e}^{{i{\mathbf{q}}{{{\mathbf{r}}}_{j}}}}}u_{{\mathbf{q}}}^{ \pm }{\kern 1pt} ,\) and the sums over six NN are

$${{\gamma }_{s}}({\mathbf{q}}) = \sum\limits_{\mathbf{d}} {{e}^{{ - i{\mathbf{qd}}}}} - 6$$
$$ = 2\left( {2\cos \frac{{\sqrt 3 }}{2}{{q}_{x}}a\cos \frac{1}{2}{{q}_{y}}a + \cos {{q}_{y}}a - 3} \right),$$
$${{\gamma }_{d}}({\mathbf{q}}) = \sum\limits_{\mathbf{d}} {{e}^{{ - i{\mathbf{qd}}}}}{{e}^{{2i{{\phi }_{d}}}}}$$
(15)
$$ = 2\left( {\cos \frac{{\sqrt 3 }}{2}{{q}_{x}}a\cos \frac{1}{2}{{q}_{y}}a - \cos {{q}_{y}}a} \right.$$
$$\left. { - \;i\sqrt 3 \sin \frac{{\sqrt 3 }}{2}{{q}_{x}}a\sin \frac{1}{2}{{q}_{y}}a} \right),$$

with the property \({{\gamma }_{{s,d}}}(0) = 0\). The zero value of diagonal components of \({{\hat {\mathcal{H}}}_{{\mathbf{q}}}}\) at \({\mathbf{q}} = 0\) is the explicit use of the above property (ii), and we will return to it below.

The dispersion law \(\omega = {{\epsilon }_{{\mathbf{q}}}}\) in the time dependence \(u_{{\mathbf{q}}}^{ \pm }(t) = {{e}^{{i\omega t}}}u_{{\mathbf{q}}}^{ \pm }\) is given by solving the equation \({\kern 1pt} {\text{det}}{\kern 1pt} (\omega {{\hat {\mathcal{K}}}_{{\mathbf{q}}}} - {{\hat {\mathcal{H}}}_{{\mathbf{q}}}}) = 0\), which yields

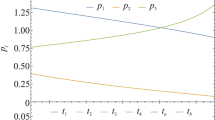
$${{\epsilon }_{{\mathbf{q}}}} = \frac{{{{{(h_{1}^{2}\gamma _{s}^{2}({\mathbf{q}}) - h_{2}^{2}{\text{|}}{{\gamma }_{d}}({\mathbf{q}}){{{\text{|}}}^{2}})}}^{{1/2}}}}}{{\pi + {{k}_{1}}{{\gamma }_{s}}({\mathbf{q}})}}.$$

We obtain numerically that \({{h}_{1}} \simeq 0.84{\kern 1pt} {{h}_{2}}\) in the whole range of relevant fields, \(b \in (0.3,0.8)\). The dependence of \({{h}_{{1,2}}}\) on b is shown in Fig. 2. We see here that both coefficients vanish simultaneously at the critical value of the field, \({{b}_{c}} \simeq 0.8\). In terms of elastic theory, discussed in [22], it corresponds to Lamé coefficients λ, μ decreasing and vanishing at \(b = {{b}_{c}}\), whereas \(\lambda \simeq 1.94\mu \), see also Eq. (19) below. The dependence of \({{\epsilon }_{{\mathbf{q}}}}\) along the symmetry lines of the Brillouin zone is shown in Fig. 3. The values of \({{\epsilon }_{{\mathbf{q}}}}\) are \(9{\text{|}}{{h}_{1}}{\text{|/}}\pi \) and \(2\sqrt {4h_{1}^{2} - h_{2}^{2}} {\text{/}}\pi \) at \({\mathbf{q}} = K\) and \({\mathbf{q}} = M\), respectively, and we have \({{\epsilon }_{{{\mathbf{q}} = M}}}{\text{/}}{{\epsilon }_{{{\mathbf{q}} = K}}} \simeq 0.71\) for all values of b. The diminishing of the gyrotropic bandwidth with b while maintaining the above ratio 0.71 is consistent with the results reported in [18]. The amplitude \({{k}_{1}}\) for the hopping contribution in the kinetic term \({{\hat {\mathcal{K}}}_{{\mathbf{q}}}}\) is negative and small, \({\text{|}}{{k}_{1}}{\text{|}} < 2 \times {{10}^{{ - 2}}}\), and we can safely ignore it in a qualitative discussion below.

Fig. 2.
figure 2

(Color online) Magnetic field dependences of the hopping constants \({{h}_{1}}\) and \({{h}_{2}}\) and the stiffness \(\mathcal{A}\).

Full size image
Fig. 3.
figure 3

(Color online) Dispersion \({{\epsilon }_{{\mathbf{q}}}}\) for different b values. Symbols Γ, M, and K correspond to the respective symmetry points in the Brillouin zone depicted in Fig. 1.

Full size image

In the limit of small wave vectors, \({\text{|}}q{\text{|}} \ll 1\), we have

$${{\epsilon }_{{\mathbf{q}}}} \simeq \frac{3}{{4\pi }}{{q}^{2}}{{a}^{2}}\sqrt {4h_{1}^{2} - h_{2}^{2}} \equiv A{{q}^{2}}.$$
(16)

The dependence of the stiffness coefficient, A, on b is also shown in Fig. 2; there is no simple proportionality between \({{h}_{{1,2}}}\) and A, since d also depends on b, see [19]. It is worthwhile to compare the value of A with the dispersion law of uniform ferromagnet. The latter case corresponds to \({{f}_{0}} \equiv 0\), and further to \(U = b\), \(V = 0\) and \({\mathbf{A}} = 0\) in (13), see Eqs. (16)–(18) in [19]. This results to \({{\epsilon }_{{\mathbf{q}}}} = {{q}^{2}} + b\), i.e., to \(\mathcal{A} = 1\) and the gapped character of the spectrum. We see that compared to the uniform ferromagnetic case, the lowest-lying part of the spectrum of SkX is gapless and its stiffness decreases with the field. One may ask, how this gapless character becomes gapful one at \({{b}_{c}}\), when the SkX dissolves. The answer is that the applicability of (16) shrinks to \(q = 0\) in this case, as \(a \to \infty \) at \({{b}_{c}}\), cf. [27].

Let us now discuss the above property (ii), which we incorporated into the definition of \({{\gamma }_{s}}({\mathbf{q}})\). Our numerical computation with the use of our trial function shows that the property \({{\hat {\mathcal{H}}}_{{\mathbf{q}}}} = 0\) at \({\mathbf{q}} = 0\) is satisfied to the accuracy of 5 × 10−3 in the range of the fields, \(0.35 < b < 0.75\). This shows rather good quality of our trial function, in accordance with our previous paper [19]. At the same time, since our trial function does not provide the exact extremum of the action, its first variation is not identically zero. In this case additional terms should be added to the effective Hamiltonian, \({{\hat {\mathcal{H}}}_{{lj}}}\) in (13), as is explained below.

We expand the variation of our function to second order in displacements,

$$\begin{gathered} \delta f = (1 + {{f}_{0}}{{{\bar {f}}}_{0}}{{)}^{{ - 1}}}\psi = \sum\limits_l \left( {u_{l}^{\alpha }{{\partial }_{\alpha }}{{f}_{1}}({\mathbf{r}} - {\mathbf{r}}_{l}^{{(0)}})} \right. \\ \left. { + \;\frac{1}{2}u_{l}^{\alpha }u_{l}^{\beta }{{\partial }_{\alpha }}{{\partial }_{\beta }}{{f}_{1}}({\mathbf{r}} - {\mathbf{r}}_{l}^{{(0)}})} \right). \\ \end{gathered} $$
(17)

This expression should be multiplied by \(\delta \mathcal{L}{\text{/}}\delta f\), which is now assumed not being identically zero. The first order term here, \( \propto {\kern 1pt} u_{l}^{\alpha }\), when integrated over r, produces the force applied to lth skyrmion out of equilibrium position. The second-order term in (17), when multiplied by \(\delta \mathcal{L}{\text{/}}\delta f\) and integrated over \({\mathbf{r}}\), adds to expression (13) in a following way.

First we note that the kinetic part of \(\delta \mathcal{L}{\text{/}}\delta f\), being symmetric in indices α, β, leads to terms proportional to full time derivatives, \( \propto {\kern 1pt} \frac{d}{{dt}}{{(u_{l}^{\alpha })}^{2}}\), which can be discarded. The potential part of the Lagrangian can be integrated by parts and the boundary term vanishes due to the rapid decrease in \({{f}_{1}}({\mathbf{r}})\) with increasing distance. The rest can be represented, after some calculation, in a form

$$\begin{array}{*{20}{l}} {\mathcal{L}'}&{ = \frac{1}{2}\sum\limits_{lj} \left( {\begin{array}{*{20}{c}} {u_{l}^{ + },}&{u_{l}^{ - }} \end{array}} \right){{{\hat {\mathcal{H}}}}_{{lj}}}\left( {\begin{array}{*{20}{c}} {u_{l}^{ - }} \\ {u_{l}^{ + }} \end{array}} \right){\kern 1pt} ,} \end{array}$$
(18)

which means that we should replace \({{\hat {\mathcal{H}}}_{{lj}}}\) in (13) by \({{\tilde {\mathcal{H}}}_{{lj}}} = {{\hat {\mathcal{H}}}_{{lj}}} - {{\delta }_{{lj}}}\sum\nolimits_m {{\hat {\mathcal{H}}}_{{lm}}}\). Clearly, if the property \(\sum\nolimits_j {{\hat {\mathcal{H}}}_{{lj}}} = 0\) is not fulfilled, due to imprecise character of our trial function, then this property is ultimately restored for the corrected form, \({{\tilde {\mathcal{H}}}_{{lj}}}\), with \(\sum\nolimits_j {{\tilde {\mathcal{H}}}_{{lj}}} = 0\). Using the symmetry of (17) in indices α, β, one can also show that \(\sum\nolimits_l {{\tilde {\mathcal{H}}}_{{lj}}} = 0\) as well. It justifies the above general property (ii) and the subtraction of number 6 in our definition of \({{\gamma }_{s}}({\mathbf{q}})\).

GREEN’S FUNCTION IN THE SMALL q LIMIT

Let us discuss now the propagation of displacements through the SkX. To simplify our discussion, we perform two subsequent rotations of our Lagrangian. First, we return to the Cartesian basis \(u_{{\mathbf{q}}}^{ \pm } = u_{{\mathbf{q}}}^{x} \pm iu_{{\mathbf{q}}}^{y}\), which corresponds to rotation \(U = \left( {\begin{array}{*{20}{c}} {1,}&{ - i} \\ {1,}&i \end{array}} \right)\). Second, we bring \({{\hat {\mathcal{H}}}_{{\mathbf{q}}}}\) to principal axes, parallel and perpendicular to \({\mathbf{q}} = q(\cos {{\phi }_{q}},\sin {{\phi }_{q}})\), by writing \((u_{{\mathbf{q}}}^{x},u_{{\mathbf{q}}}^{y}) = (u_{{\mathbf{q}}}^{\parallel },u_{{\mathbf{q}}}^{ \bot })U_{1}^{\dag }\) with \({{U}_{1}} = \left( {\begin{array}{*{20}{c}} {\cos {{\phi }_{q}},}&{ - \sin {{\phi }_{q}}} \\ {\sin {{\phi }_{q}},}&{\cos {{\phi }_{q}}} \end{array}} \right)\). As a result, we reduce the Lagrangian to the form

$$\mathcal{L} = \frac{1}{2}\sum\limits_{\mathbf{q}} \left( {\begin{array}{*{20}{c}} {u_{{ - {\mathbf{q}}}}^{\parallel },}&{u_{{ - {\mathbf{q}}}}^{ \bot }} \end{array}} \right)\left( {\begin{array}{*{20}{c}} { - {{A}_{\parallel }}{{q}^{2}},}&{ - 2\pi {{\partial }_{t}}} \\ {2\pi {{\partial }_{t}},}&{ - {{A}_{ \bot }}{{q}^{2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {u_{{\mathbf{q}}}^{\parallel }} \\ {u_{{\mathbf{q}}}^{ \bot }} \end{array}} \right),$$
$${{A}_{\parallel }} = - \frac{3}{2}(2{{h}_{1}} + {{h}_{2}}){{a}^{2}},\quad {{A}_{ \bot }} = - \frac{3}{2}(2{{h}_{1}} - {{h}_{2}}){{a}^{2}},$$
(19)

with \({{A}_{\parallel }},{{A}_{ \bot }} > 0\) are two elastic moduli, that would correspond to longitudinal and transverse sound modes in situation with phonons; we have \({{A}_{\parallel }}{{A}_{ \bot }} = 2\pi \mathcal{A}\). The different form of the kinetic term in our case makes the dispersion quadratic, instead of linear dispersion law for acoustic phonons; it also shows that the displacement \(2\pi {\kern 1pt} u_{{ - {\mathbf{q}}}}^{ \bot }\) is a canonically conjugate momentum to \(u_{{\mathbf{q}}}^{\parallel }\).

It allows us to second quantize our theory, along the guidelines in [19, 28]. We demand \([u_{{\mathbf{q}}}^{\parallel },2\pi {\kern 1pt} u_{{ - {\mathbf{q}}}}^{ \bot }] = i\hbar \) (we set \(\hbar = 1\)) and find

$$\begin{gathered} u_{{\mathbf{q}}}^{\parallel } = \frac{1}{{\sqrt {4\pi \varkappa } }}(c_{{\mathbf{q}}}^{\dag }{{e}^{{i{{\epsilon }_{{\mathbf{q}}}}t}}} + {{c}_{{ - {\mathbf{q}}}}}{{e}^{{ - i{{\epsilon }_{{\mathbf{q}}}}t}}}){\kern 1pt} , \\ u_{{\mathbf{q}}}^{ \bot } = i\frac{{\sqrt \varkappa }}{{\sqrt {4\pi } }}(c_{{\mathbf{q}}}^{\dag }{{e}^{{i{{\epsilon }_{{\mathbf{q}}}}t}}} - {{c}_{{ - {\mathbf{q}}}}}{{e}^{{ - i{{\epsilon }_{{\mathbf{q}}}}t}}}), \\ \end{gathered} $$
(20)

where asymmetry parameter, \(\varkappa = \sqrt {{{A}_{\parallel }}{\text{/}}{{A}_{ \bot }}} \simeq 1.98\). In terms of creation (annihilation) operators, \(c_{{\mathbf{q}}}^{\dag }\) (\({{c}_{{\mathbf{q}}}}\)), the Hamiltonian becomes \(\hat {\mathcal{H}} = \sum\nolimits_{\mathbf{q}} {{\epsilon }_{{\mathbf{q}}}}c_{{\mathbf{q}}}^{\dag }{{c}_{{\mathbf{q}}}}\).

The retarded Green’s function is defined as

$$\begin{array}{*{20}{l}} {G(t,{\mathbf{q}})}&{ = - i\vartheta (t)\left( {\begin{array}{*{20}{c}} {[u_{{ - {\mathbf{q}}}}^{x}(t),u_{{\mathbf{q}}}^{x}],}&{[u_{{ - {\mathbf{q}}}}^{x}(t),u_{{\mathbf{q}}}^{y}]} \\ {[u_{{ - {\mathbf{q}}}}^{y}(t),u_{{\mathbf{q}}}^{x}],}&{[u_{{ - {\mathbf{q}}}}^{y}(t),u_{{\mathbf{q}}}^{y}]} \end{array}} \right){\kern 1pt} ,} \end{array}$$
(21)

and its Fourier transform at \(t > 0\) is given by

$$G(t,{\mathbf{r}}) = - \frac{{\sqrt 3 {{a}^{2}}}}{{4\pi }}$$
$$ \times \;\int \frac{{{{d}^{2}}{\mathbf{q}}}}{{{{{(2\pi )}}^{2}}}}{{e}^{{i{\mathbf{qr}}}}}{{U}_{1}}\left( {\begin{array}{*{20}{c}} {\frac{1}{\varkappa }\sin {{\epsilon }_{{\mathbf{q}}}}t,}&{ - \cos {{\epsilon }_{{\mathbf{q}}}}t} \\ {\cos {{\epsilon }_{{\mathbf{q}}}}t,}&{\varkappa \sin {{\epsilon }_{{\mathbf{q}}}}t} \end{array}} \right)U_{1}^{\dag }.$$

A simple calculation (effectively restricting the integration over \(q \leqslant {{a}^{{ - 1}}}\) by the Gaussian form, \(\exp ( - {{q}^{2}}{{a}^{2}})\)) leads to the expression, valid for large times and distances, \(t\mathcal{A} \gg ra\), \(r \gg a\),

$$G(t,{\mathbf{r}}) = \frac{{\sqrt 3 {{a}^{2}}}}{{16{{\pi }^{2}}t\mathcal{A}}}\left[ { - \cos ({{r}^{2}}{\text{/}}4t\mathcal{A})\frac{{\varkappa + {{\varkappa }^{{ - 1}}}}}{2}\left( {\begin{array}{*{20}{c}} {1,}&0 \\ {0,}&1 \end{array}} \right)} \right.$$
$$ + \;\sin ({{r}^{2}}{\text{/}}4t\mathcal{A})\left( {\begin{array}{*{20}{c}} {0,}&1 \\ { - 1,}&0 \end{array}} \right)$$
$$\left. { + \;F({{r}^{2}}{\text{/}}4t\mathcal{A})\frac{{\varkappa - {{\varkappa }^{{ - 1}}}}}{2}\left( {\begin{array}{*{20}{c}} {\cos 2\phi ,}&{\sin 2\phi } \\ {\sin 2\phi ,}&{ - \cos 2\phi } \end{array}} \right)} \right],$$
$$F(z) = \cos z - \sin z{\text{/}}z.$$
(22)

At shorter distances, \(r \ll \sqrt {t\mathcal{A}} \), the first term in \(G(t,{\mathbf{r}})\) is dominant, indicating the isotropic propagation. At intermediate distances, \(\sqrt {t\mathcal{A}} \ll r \ll t\mathcal{A}{\text{/}}a\), the combination of the first and third terms shows the anisotropy of tensor \(G(t,{\mathbf{r}})\), with the main axes along and perpendicular to vector r in plane. For long distances, \(r \gg t\mathcal{A}{\text{/}}a\), the function \(G(t,{\mathbf{r}})\) becomes (exponentially) small, meaning that the propagation has not yet reached the point r. Notice that the oscillating factors depend only on the ratio \({{r}^{2}}{\text{/}}t\), and the mentioned anisotropy concerns the relative weight of correlations of \({{u}^{x}}\) and \({{u}^{y}}\). We illustrate this behavior in Fig. 4 by plotting two principal components, \({{G}_{\parallel }}(t,{\mathbf{r}})\) and \({{G}_{ \bot }}(t,{\mathbf{r}})\), for pairwise correlations of \({{u}^{\parallel }}\) and \({{u}^{ \bot }}\), respectively.

Fig. 4.
figure 4

Green’s functions \({{G}_{\parallel }}(t,{\mathbf{r}})\) and \({{G}_{ \bot }}(t,{\mathbf{r}})\) plotted for \(t = 6{{\mathcal{A}}^{{ - 1}}}{{a}^{2}}\), describing pairwise correlation for displacements \({{u}^{\parallel }}\) and \({{u}^{ \bot }}\) parallel and perpendicular to r, respectively.

Full size image

CONCLUSIONS

We develop a theory of the lowest lying Goldstone mode of the skyrmion lattice, also known as gyrotropic mode. This mode describes the displacements of skyrmions as whole objects and leads to equation of motion in the form of collective Thiele equation. The spectrum is quadratic at small wavevectors, and this property stems in our approach from the elastic form of the potential and Berry phase kinetic term of the action. The elastic potential follows from the treatment of skyrmions as individual topological objects and does not assume more demanding theoretical description of phasons, three magnetic helices etc. On the same ground, the quadratic character of the spectrum is robust to inclusion of dipolar interaction or anisotropies as long as SkX is intact. The propagation of perturbation through the skyrmion lattice is anisotropic at intermediate distances. The width of this lowest band monotonically decreases with the magnetic field and disappears at the critical field, marking the transition to the uniform ferromagnetic state.