Recently, new experimental data have appeared on the cross section of \({{e}^{ + }}{{e}^{ - }} \to \Lambda \bar {\Lambda }\) annihilation near the threshold [1]. These data are consistent with the results of previous works [2–4], but have much higher accuracy. All these results demonstrate a strong energy dependence of the cross section near the threshold. A similar phenomenon has been observed in such processes as \({{e}^{ + }}{{e}^{ - }} \to p\bar {p}\) [5–12], \({{e}^{ + }}{{e}^{ - }} \to n\bar {n}\) [13–15], \({{e}^{ + }}{{e}^{ - }} \to {{\Lambda }_{c}}{{\bar {\Lambda }}_{c}}\) [16], [17], \({{e}^{ + }}{{e}^{ - }} \to B\bar {B}\) [18], and others. In all these cases the shapes of near-threshold resonances differ significantly from the standard Breit–Wigner parameterization. The origin of the phenomenon is naturally explained by the strong interaction of produced particles near the threshold (the so-called final-state interaction). Since a typical value of the corresponding potential is rather large (hundreds of MeV), existence of either low-energy bound state or virtual state is possible. In the latter case a small deepening of the potential well leads to appearance of a real low-energy bound state. In both cases, the value of the wave function (or its derivative) inside the potential well significantly exceeds the value of the wave function without the final-state interaction. As a result, the energy dependence of the wave function inside the potential well is very strong. Since quarks in \({{e}^{ + }}{{e}^{ - }}\) annihilation are produced at small distances of the order of \({\text{1/}}\sqrt s \), a strong energy dependence of the cross section is determined solely by the energy dependence of the wave function of produced pair of hadrons at small distances. Such a natural approach made it possible to describe well the energy dependence of almost all known near-threshold resonances (see [19–25] and references therein).

The annihilation \({{e}^{ + }}{{e}^{ - }} \to \Lambda \bar {\Lambda }\) near the threshold is the simplest for investigation. This is due to the fact that the \(\Lambda \bar {\Lambda }\) system has a fixed isotopic spin \(I = 0\), and the pair is produced mainly in the state with an angular momentum \(l = 0\) (the contribution of state with \(l = 2\) can be neglected). Moreover, there is no Coulomb interaction between \(\Lambda \) and \(\bar {\Lambda }\). Our analysis shows that the imaginary part of the optical potential of \(\Lambda \bar {\Lambda }\) interaction, which takes into account the possibility of annihilation of \(\Lambda \bar {\Lambda }\) pair into mesons, has only little effect on the cross section. Therefore, we neglect the imaginary part of the potential. Finally, we describe the cross section of the process \({{e}^{ + }}{{e}^{ - }} \to \Lambda \bar {\Lambda }\) by a simple analytical formula (see [25] and references therein for more details):

$$\sigma = \frac{{2\pi \beta {{\alpha }^{2}}}}{s}{{g}^{2}}F_{D}^{2}(s){{\left| {\psi (0)} \right|}^{2}},$$
(1)

where \(\beta = k{\text{/}}{{M}_{\Lambda }}\) is the baryon velocity, \(k = \sqrt {{{M}_{\Lambda }}E} \), \(s = {{\left( {2{{M}_{\Lambda }} + E} \right)}^{2}}\), \(E\) is the kinetic energy of the pair, \({{F}_{D}}(s)\) = \({{\left( {1 - s{\text{/}}{{\Lambda }^{2}}} \right)}^{{ - 2}}}\) is the dipole form factor, and \(\Lambda \) is some parameter close to 1 GeV. The factor \(g\) is related to the probability of pair production at small distance \( \sim {\kern 1pt} {\text{1/}}\sqrt s \) and can be considered as a constant independent of energy. In Eq. (1), \(\psi (0)\) is the wave function of \(\Lambda \bar {\Lambda }\) pair at \(r = 0\).

The cross section (1) is enhanced by the factor \({{\left| {\psi (0)} \right|}^{2}} \gg 1\) if there is a loosely bound state or a virtual state of \(\Lambda \bar {\Lambda }\) pair. In both cases the modulus of scattering length \(a\) of \(\Lambda \) and \(\bar {\Lambda }\) is large compared to the characteristic radius \(R\) of \(\Lambda \bar {\Lambda }\) interaction potential, \(\left| a \right| \gg R\). For a loosely bound state \(a\) is positive and the binding energy is \(\varepsilon = - {\text{1/}}{{M}_{\Lambda }}{{a}^{2}}\). For a virtual state \(a\) is negative and the energy of virtual state is defined as \(\varepsilon = {\text{1/}}{{M}_{\Lambda }}{{a}^{2}}\). In both cases \(\left| \varepsilon \right|\) is much smaller than the characteristic depth of the potential well. The energy dependence of \({{\left| {\psi (0)} \right|}^{2}}\) for near-threshold resonances is more or less universal and is determined by the scattering length \(a\) and the effective radius of interaction [26]. Therefore, one can use any convenient form of potential \(U(r)\) for description of near-threshold resonances.

In the present paper we parametrize the potential as \(U(r)\) = \( - {{U}_{0}}\theta (R - r)\). For this potential, the energy dependence of \({{\left| {\psi (0)} \right|}^{2}}\) is well-known (see, e.g., [26]):

$$\begin{gathered} {{\left| {\psi (0)} \right|}^{2}} = \frac{{{{q}^{2}}}}{{{{q}^{2}}{{{\cos }}^{2}}\left( {qR} \right) + {{k}^{2}}{{{\sin }}^{2}}\left( {qR} \right)}}, \\ q = \sqrt {{{M}_{\Lambda }}(E + {{U}_{0}})} . \\ \end{gathered} $$
(2)

Near the threshold \(k \ll q\) and the cross section (1) is enhanced if

$${{q}_{0}}R \approx \pi \left( {n + \frac{1}{2}} \right) + \delta ,\quad \left| \delta \right| \ll 1,$$
(3)

where \({{q}_{0}} = \sqrt {{{M}_{\Lambda }}{{U}_{0}}} \), and \(n\) is an integer. For \(\left| \delta \right| \ll 1\), the scattering length is \(a = {\text{1/}}{{q}_{0}}\delta \), where \(\delta > 0\) for the bound state, and \(\delta < 0\) for the virtual state.

By means of Eq. (3) the expression (2) can be simplified:

$$\begin{gathered} {{\left| {\psi (0)} \right|}^{2}} \approx \frac{{\gamma {{U}_{0}}}}{{{{{\left( {E + {{\varepsilon }_{0}}} \right)}}^{2}} + \gamma E}}, \\ \gamma = 4{{\kappa }^{2}}{{U}_{0}},\quad {{\varepsilon }_{0}} = 2\delta \kappa {{U}_{0}},\quad \kappa = \frac{1}{{\pi (n + {\text{1/2}})}}. \\ \end{gathered} $$
(4)

The corresponding energy dependence of the cross section (1) is equivalent to the Flatté formula [27], which is expressed in terms of the scattering length and the effective radius \({{r}_{0}}\) of interaction. Note that for the rectangular potential well \({{r}_{0}} = R\). One can easily verify that the precise and approximate formulas for the cross section are in good agreement with each other for \(\left| \delta \right| \ll 1\) and \(E \lesssim {{\varepsilon }_{0}} \ll {{U}_{0}}\). Note that \(\left| {{{\varepsilon }_{0}}} \right| \gg \left| \varepsilon \right|\) for both bound and virtual states, namely \({{\varepsilon }_{0}} \approx 2\left| \varepsilon \right|a{\text{/}}R\). However, the position of peak in the cross section, which is proportional to \(\sqrt E {{\left| {\psi (0)} \right|}^{2}}\), is located at energy \(E \approx \left| \varepsilon \right|\) for both bound and virtual states.

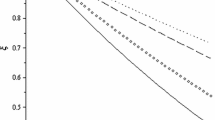
In Fig. 1, we show our predictions for the cross section compared to experimental data [1], as well as the enhancement factor \({{\left| {\psi (0)} \right|}^{2}}\). The parameters of the model are \({{U}_{0}} = 584{\kern 1pt} \) MeV, \(R = 0.45{\kern 1pt} \) fm, and \(g = 0.2\). In the energy region under consideration the dependence of our predictions on the parameter \(\Lambda \) is very weak. To be specific, we set \(\Lambda = 1{\kern 1pt} \) GeV. Our model, giving \({{\chi }^{2}}{\text{/}}{{N}_{{{\text{df}}}}}\) = 9.8/13, provides a good description of experimental data [1]. Note that account for the enhancement factor \({{\left| {\psi (0)} \right|}^{2}}\) is of great importance for correct description of experimental data.

Fig. 1.
figure 1

(Color online) Cross section of \({{e}^{ + }}{{e}^{ - }} \to \Lambda \bar {\Lambda }\) annihilation (left) and the enhancement factor \({{\left| {\psi (0)} \right|}^{2}}\) (right) as the functions of energy \(E\). The parameters of the potential are \({{U}_{0}} = 584{\kern 1pt} \) MeV and \(R = 0.45{\kern 1pt} \) fm. Experimental data are taken from [1].

Full size image

Within our model, we also predict a bound state with the binding energy \({{E}_{0}} \approx - 30{\kern 1pt} \) MeV. Observation of this bound state would be very important. The results of [28–36] indicate the anomalous behavior of the cross sections \({{e}^{ + }}{{e}^{ - }} \to {{K}^{ + }}{{K}^{ - }}{{\pi }^{ + }}{{\pi }^{ - }}\), \({{e}^{ + }}{{e}^{ - }} \to 2\left( {{{K}^{ + }}{{K}^{ - }}} \right)\), \({{e}^{ + }}{{e}^{ - }} \to \phi {{K}^{ + }}{{K}^{ - }}\), and others at \(\sqrt s \approx 2.2{\kern 1pt} \) GeV (this value of \(s\) corresponds to \(E \approx - 30{\kern 1pt} \) MeV). However, a more detailed study of this energy region is required.

In conclusion, the assumption of existence of a low-energy real or virtual state has allowed us to describe perfectly recent and previous experimental data for the cross section of \({{e}^{ + }}{{e}^{ - }} \to \Lambda \bar {\Lambda }\) annihilation near the threshold. Our model indicates possible existence of a bound \(\Lambda \bar {\Lambda }\) state with energy \(E \approx - 30{\kern 1pt} \) MeV.