Light-Shining-Through-Wall Cavity Setups for Probing Axion-Like Particles

We discuss the aspects of axion-like-particles searches with Light-Shining-through-Wall experimental setups consisted of two radio-frequency cavities. We compare the efficiencies of four setups which involve the cavity pump modes and external magnetic fields. Additionally, we discuss the sensitivity dependence both on the relative position of two cylindrical cavities and on their radius-to-length ratio.

INTRODUCTION

Light feebly-interacting pseudoscalar particles appear in modern particle physics in various ways. Originally, a pseudoscalar particle called an axion was proposed in late 1970s to explain the strong CP problem in quantum chromodynamics [1, 2].¹ More general axion-like-particles (ALPs) are motivated by the string theory and appear in its low-energy phenomenological description [3–5]. In addition to the motivation for the particle physics models, axions and ALPs are of a great interest in cosmology because they could make up a significant fraction of the dark matter in the Universe [6–8].

The Lagrangian for interacting ALPs and photons can be written as follows

$$\begin{gathered} \mathcal{L} = - \frac{1}{4}{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}} + \frac{1}{2}{\kern 1pt} {{\partial }_{\mu }}a{\kern 1pt} {{\partial }^{\mu }}a \\ - \;\frac{1}{2}{\kern 1pt} m_{a}^{2}{{a}^{2}} - \frac{1}{4}{\kern 1pt} {{g}_{{a\gamma \gamma }}}a{{F}_{{\mu \nu }}}{{{\tilde {F}}}^{{\mu \nu }}}, \\ \end{gathered} $$

(1)

where ${{F}_{{\mu \nu }}}$ is the electromagnetic tensor and ${{\tilde {F}}^{{\mu \nu }}} = \frac{1}{2}{{\epsilon }^{{\mu \nu \alpha \beta }}}{{F}_{{\alpha \beta }}}$ is its dual, $a$ is the ALP field of mass ${{m}_{a}}$ with dimensionful photon–axion coupling ${{g}_{{a\gamma \gamma }}}$. The natural system of units $\hbar = c = {{k}_{{\text{B}}}} = 1$ is used. Generally, ${{m}_{a}}$ and ${{g}_{{a\gamma \gamma }}}$ are treated as independent parameters.

A popular strategy of ALP searches is related to the cosmological (dark matter) and astrophysical probing. These ALPs can be detected by ground-based haloscopes (detection of dark matter ALPs) and helioscopes (ALPs can be produced hypothetically in the Sun) [9] (see, e.g., [10] for a recent review).

Another approach to probing ALPs implies both their production and detection in a laboratory, and usually called Light-Shining-through-Wall (LSW) experiments [11–14]. The LSW setups consist of two cavities separated by a non-transparent wall. ALPs are produced in the first cavity by interaction of electromagnetic field components. Generated ALPs can pass through the wall and convert back to photons in the detection cavity. High intensity of initial electromagnetic field and the resonant amplification for the signal inside the cavities are required because of the extremely small coupling ${{g}_{{a\gamma \gamma }}}$. Two wavelength ranges of EM fields are applicable to LSW: the optical range setup including high intensity lasers and the radio range setup consisting of radio frequency cavities with high quality factors. Both ideas were realized in the experiments, ALPS (optical) [19] and CROWS (radio) [20]. These experiments set the bound ${{g}_{{a\gamma \gamma }}} \simeq {{10}^{{ - 7}}}$ GeV^–1 for a wide range of ALP masses. However, this bound is three orders of magnitude weaker than the CAST helioscope limit ${{g}_{{a\gamma \gamma }}} \lesssim$ 6 × 10^‒11 GeV^–1 [9]. For the moment, the ALPS-II laser experiment [21] is under construction and its projected sensitivity exceeds CAST level.

In addition, the LSW radio experiments aimed at the ALP searches are of a great interest [22]. Recently, several proposals with LSW radio cavities appeared in the literature including superconducting radio frequency (SRF) cavities [23–25]. In this letter we compare different LSW cavity setups including modification of the CROWS [14, 20]. Specifically, we study four setups: (i) an electromagnetic pump mode plus static magnetic field in the emitter cavity, static magnetic field in the receiver cavity [14]; (ii) two electromagnetic pump modes in the emitter cavity; an electromagnetic pump mode in the receiver cavity [23]; (iii) two electromagnetic pump modes in the emitter cavity, static magnetic field in receiver cavity [24]; (iv) an electromagnetic pump mode plus static magnetic field in the emitter cavity, an electromagnetic pump mode in the receiver cavity.

Another aspect of our analysis is geometry of the setup which can be adjusted in order to achieve higher sensitivity to ALPs parameters. We study transfer of ALPs from the emitter to the receiver for all aforementioned designs (i–iv) and discuss their optimal configuration, either coaxial or parallel (see, e. g., Fig. 1 for detail). Further, we investigate ${{g}_{{a\gamma \gamma }}}$ sensitivity dependence on the radius-to-length ratio of production cylindrical cavity.

Fig. 1.

Two specific types of the experimental configuration consisting of two cylindrical cavities with (left panel) coaxial or (right panel) parallel orientation and screened by axion-penetrable wall. Wavy and solid lines represent electromagnetic field (cavity mode or magnetic field) and ALPs, respectively.

AXION ELECTRODYNAMICS

We briefly review the axion electrodynamics with the Lagrangian (1). The Euler–Lagrange equation for the ALP field reads,

$$({{\partial }_{\mu }}{{\partial }^{\mu }} + m_{a}^{2}){\kern 1pt} a = - \frac{1}{4}{\kern 1pt} {{g}_{{a\gamma \gamma }}}{\kern 1pt} {{F}_{{\mu \nu }}}{{\tilde {F}}^{{\mu \nu }}}\;,$$

(2)

while the Maxwell’s equations with an ALP-induced current read,

$${{\partial }_{\mu }}{{F}^{{\mu \nu }}} = - {{g}_{{a\gamma \gamma }}}{\kern 1pt} {{\partial }_{\mu }}a{\kern 1pt} {{\tilde {F}}^{{\mu \nu }}}\;.$$

(3)

One can rewrite Eqs. (2) and (3) in terms of the electric and magnetic fields,

$$({{\partial }_{\mu }}{{\partial }^{\mu }} + m_{a}^{2}){\kern 1pt} a = {{g}_{{a\gamma \gamma }}}({\mathbf{E}} \cdot {\mathbf{B}}),$$

(4)

$$(\nabla \cdot {\mathbf{E}}) = {{\rho }_{a}},\quad [\nabla \times {\mathbf{B}}] = {\mathbf{\dot {E}}} + {{{\mathbf{j}}}_{a}},$$

(5)

where the density of charge ${{\rho }_{a}}$ and current ${{{\mathbf{j}}}_{a}}$ are given by the expressions

$${{\rho }_{a}} = - {{g}_{{a\gamma \gamma }}}(\nabla a \cdot {\mathbf{B}}),\quad {{{\mathbf{j}}}_{a}} = {{g}_{{a\gamma \gamma }}}([\nabla a \times {\mathbf{E}}] + \dot {a}{\mathbf{B}}).$$

(6)

Aforementioned equations describe a way to produce ALPs by the electromagnetic field and the approach to detection of the ALP field in presence of background electromagnetic field. We further elaborate on this idea to compare the sensitivities of four types of the LSW setup for probing ALPs.

EMITTER CAVITY

In this section, we consider the ALPs production. It is worth noting that Eq. (4) implies the invariant ${{F}_{{\mu \nu }}}{{\tilde {F}}^{{\mu \nu }}} = - 4({\mathbf{E}} \cdot {\mathbf{B}})$ should be non-zero in order to produce ALPs by the electromagnetic field. Following this requirement, we consider two options for the production of ALPs using radiofrequency (RF) cavities:

(i) a normally conducting RF cavity with a single pump mode with frequency ${{\omega }_{0}}$ immersed in a strong static magnetic field ${{{\mathbf{B}}}_{{\operatorname{ext} }}}$. We use the notation MF emitter (i.e., pump mode (M) + magnetic field (F)) for this case throughout the paper;

(ii) a superconducting RF cavity with two pump modes at frequencies ${{\omega }_{{1,2}}}$. We use notation MM emitter (pump mode (M) + pump mode (M)) for this setup.

It is worth mentioning that in the steady regime both EM-source (right-hand side of Eq. (4)) and the induced axion field have the same frequency ${{\omega }_{a}}$. For the MF emitter case, the source function in the Eq. (4) contains a single component oscillating at the frequency ${{\omega }_{a}} = {{\omega }_{0}}$. However, for the MM emitter case, there are two components at frequencies ${{\omega }_{a}} = {{\omega }_{ \pm }} = {{\omega }_{2}} \pm {{\omega }_{1}}$ (${{\omega }_{2}} > {{\omega }_{1}}$). As a result, each particular combination of the field for both MF emitter and MM emitter can be written in the general form,

$$f(t,{\mathbf{x}}) = {{g}_{{a\gamma \gamma }}}E_{{\text{0}}}^{{{\text{em}}}}B_{{\text{0}}}^{{{\text{em}}}}\operatorname{Re} \left[ {({\mathbf{e}} \cdot {\mathbf{b}})({\mathbf{x}}) \cdot {{e}^{{ - i{{\omega }_{a}}t}}}} \right],$$

(7)

where $E_{0}^{{{\text{em}}}},B_{0}^{{{\text{em}}}}$ are typical values of the emitter EM fields, $({\mathbf{e}} \cdot {\mathbf{b}})({\mathbf{x}})$ is a dimensionless function determined by the production approach.

For the RF cavity that emits the ALPs (MF emitter), $E_{{\text{0}}}^{{{\text{em}}}}$ is a typical amplitude of pump mode taken on the cavity wall,²$B_{{\text{0}}}^{{{\text{em}}}}$ is a magnitude of the static magnetic field, and the typical combination of the normalized fields in Eq. (7) can be written as follows

$$({\mathbf{e}} \cdot {\mathbf{b}})({\mathbf{x}}) = ({{{\mathbf{e}}}_{0}}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{{\operatorname{ext} }}}),$$

(8)

where ${{{\mathbf{e}}}_{0}}({\mathbf{x}})$ is a dimensionless electric field of the pump mode, and ${{{\mathbf{b}}}_{{\operatorname{ext} }}}$ is a unit vector that is collinear to the magnetic field direction.

For the MM emitter case, $E_{{\text{0}}}^{{{\text{em}}}}$ and $B_{{\text{0}}}^{{{\text{em}}}}$ represent the surface electric and magnetic fields amplitudes of both pump modes and the dimensionless functions in Eq. (7) can be written for ${{\omega }_{a}} = {{\omega }_{ + }}$ and ${{\omega }_{a}} = {{\omega }_{ - }}$ as f-ollows

$${{({\mathbf{e}} \cdot {\mathbf{b}})}_{ + }}({\mathbf{x}}) = \frac{1}{2}\left[ {({{{\mathbf{e}}}_{1}}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{2}}({\mathbf{x}})) + ({{{\mathbf{e}}}_{2}}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{1}}({\mathbf{x}}))} \right],$$

(9)

$${{({\mathbf{e}} \cdot {\mathbf{b}})}_{ - }}({\mathbf{x}}) = \frac{1}{2}\left[ {({\mathbf{e}}_{1}^{*}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{2}}({\mathbf{x}})) + ({{{\mathbf{e}}}_{2}}({\mathbf{x}}) \cdot {\mathbf{b}}_{1}^{*}({\mathbf{x}}))} \right],$$

(10)

where ${{{\mathbf{e}}}_{i}}({\mathbf{x}})$, ${{{\mathbf{b}}}_{i}}({\mathbf{x}})$, $i = 1,2$, are dimensionless electric and magnetic fields of pump modes.

Equation (4) implies the following solution,

$$\begin{gathered} a(t,{\mathbf{x}}) = {{g}_{{a\gamma \gamma }}}E_{{\text{0}}}^{{{\text{em}}}}B_{{\text{0}}}^{{{\text{em}}}}\int\limits_{{{V}_{{{\text{em}}}}}} {{{d}^{3}}{\mathbf{x}}{\kern 1pt} '\operatorname{Re} \left[ {({\mathbf{e}} \cdot {\mathbf{b}})({\mathbf{x}}{\kern 1pt} ')\frac{{{{e}^{{i{{k}_{a}}|{\mathbf{x}} - {\mathbf{x}}'| - i{{\omega }_{a}}t}}}}}{{4\pi \left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right|}}} \right]} \\ \equiv \operatorname{Re} \left[ {a({\mathbf{x}}){{e}^{{ - i{{\omega }_{a}}t}}}} \right], \\ \end{gathered} $$

(11)

where ${{k}_{a}} = \sqrt {\omega _{a}^{2} - m_{a}^{2}}$ are typical momenta of the produced ALPs, integration is performed over the emitter volume ${{V}_{{{\text{em}}}}}$. For MF emitter, the dimensionless factor in Eq. (11) is defined by Eq. (8). However, for MM emitter the solution of Eq. (4) splits into two frequency components ${{\omega }_{ \pm }}$. Note that the produced ALPs of frequency component ${{\omega }_{ - }}$ is at least an order of magnitude smaller than ${{\omega }_{ + }}$ component [24], so further we deal with ${{\omega }_{ + }}$ only. One can replace formally $i{{k}_{a}}$ with $- {{\kappa }_{a}} = - \sqrt {m_{a}^{2} - \omega _{a}^{2}}$ in Eq. (11) for the relatively heavy ALP mass limit ${{m}_{a}} \gtrsim {{\omega }_{a}}$. Then the ALP field amplitude decreases exponentially as $a({\mathbf{x}}) \propto \exp \left( { - {{\kappa }_{a}}\left| {\mathbf{x}} \right|} \right){\text{/}}\left| {\mathbf{x}} \right|$ outside the production cavity. Therefore, the detecting cavity signal is suppressed for ${{m}_{a}} \gtrsim {{\omega }_{a}}$ mass range.

RECEIVER CAVITY

In this section, we investigate the issue of the ALP signal detection in the receiver cavity. A resonant generation of electromagnetic modes in the detecting cavity caused by the axion-induced current, $j_{a}^{\nu } = ({{\rho }_{a}},{{{\mathbf{j}}}_{a}})$ where the density of the effective charge ${{\rho }_{a}}({\mathbf{x}},t)$ and the effective current ${{{\mathbf{j}}}_{a}}({\mathbf{x}},t)$ are given by Eqs. (6). Two options are assumed for detection:

(i) the receiver cavity is a normally conducting one, and it is immersed magnetic field ${{{\mathbf{B}}}_{{\operatorname{ext} }}}$. We use the notation M*F receiver (induced signal mode (M*) + magnetic field (F) of the receiver) for that case (the label M* denotes the mode that we expect to detect throughout the paper);

(ii) the receiver cavity is superconducting, and it is pumped by the detecting mode. We use the notation M*M receiver (induced signal mode (M*) + pump mode (M) of the receiver) for this setup of the cavity.

One can show (see, e.g., [26] and references therein for detail) that generating field is a combination of solenoidal and potential modes, however only the solenoidal modes can be resonantly enhanced. The typical magnitude of the signal can be characterized by the expression [23, 25]

$$G = - \frac{{{{Q}_{{{\text{rec}}}}}}}{{{{\omega }_{s}}}}\frac{1}{{{{V}_{{{\text{rec}}}}}}}\int\limits_{{{V}_{{{\text{rec}}}}}} {{{d}^{3}}{\mathbf{x}}({\mathbf{e}}_{s}^{*} \cdot {{{\mathbf{j}}}_{a}}),} $$

(12)

where ${{Q}_{{{\text{rec}}}}}$ is a quality factor for the receiver eigenmode that depends on the electric field near the cavity walls and corresponding power losses due to non-linearities (see [27] and references therein for details), ${{V}_{{{\text{rec}}}}}$ is the volume of the receiver cavity, ${{\omega }_{s}}$ is a frequency of the receiver signal eigenmode, and ${{{\mathbf{e}}}_{s}}({\mathbf{x}})$ is a dimensionless signal eigenmode that is normalized as follows [25]

$$\int\limits_{{{V}_{{{\text{rec}}}}}} {{d}^{3}}{\mathbf{x}}{{\left| {{{{\mathbf{e}}}_{s}}({\mathbf{x}})} \right|}^{2}} = {{V}_{{{\text{rec}}}}}.$$

(13)

The specific form of the current ${{{\mathbf{j}}}_{a}}$ in the Eq. (12) depends on the way of ALP detection. It is remarkable that the general expression of the overlapping integral in Eq. (12) for both M*F and M*M receivers can be written in the following explicit form

$$\int\limits_{{{V}_{{{\text{rec}}}}}} {{d}^{3}}{\mathbf{x}}({\mathbf{e}}_{s}^{*} \cdot {{{\mathbf{j}}}_{a}}) = - i{{\omega }_{s}}{{g}_{{a\gamma \gamma }}}B_{0}^{{{\text{rec}}}}\int\limits_{{{V}_{{{\text{rec}}}}}} {{d}^{3}}{\mathbf{x}}({\mathbf{e}} \cdot {\mathbf{b}})\text{*}{\kern 1pt} ({\mathbf{x}})a({\mathbf{x}}),$$

(14)

where $B_{{\text{0}}}^{{{\text{rec}}}}$ is a characteristic magnetic field of the detection cavity and $({\mathbf{e}} \cdot {\mathbf{b}})\text{*}{\kern 1pt} ({\mathbf{x}})$ is a dimensionless complex-conjugated function that is associated with a specific way of ALP detection.

More specifically, for the M*F receiver, $B_{{\text{0}}}^{{{\text{rec}}}}$ is the value of the external magnetic field, and dimensionless function has the following form external magnetic field and

$$({\mathbf{e}} \cdot {\mathbf{B}})\text{*}{\kern 1pt} ({\mathbf{x}}) = ({{{\mathbf{e}}}_{s}}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{{\operatorname{ext} }}})\text{*}{\kern 1pt} ,$$

(15)

where ${{{\mathbf{b}}}_{{\operatorname{ext} }}}$ is a unit vector co-directed with a magnetic field inside the receiver cavity.

For the M*M receiver, $B_{{\text{0}}}^{{{\text{rec}}}}$ is the magnetic field amplitude of the pump mode and the combinations of dimensionless functions are given by

$$({\mathbf{e}} \cdot {\mathbf{b}})_{ + }^{*}({\mathbf{x}}) = \frac{1}{2}\left[ {({{{\mathbf{e}}}_{s}}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{d}}({\mathbf{x}})) + ({{{\mathbf{e}}}_{d}}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{s}}(x))} \right]\text{*}{\kern 1pt} ,$$

(16)

$$({\mathbf{e}} \cdot {\mathbf{b}})_{ - }^{*}({\mathbf{x}}) = \frac{1}{2}[({{{\mathbf{b}}}_{s}}({\mathbf{x}}) \cdot {\mathbf{b}}_{d}^{*}({\mathbf{x}})) + ({\mathbf{e}}_{d}^{*}({\mathbf{x}}) \cdot {{{\mathbf{b}}}_{s}}({\mathbf{x}}))]\text{*}{\kern 1pt} ,$$

(17)

for ${{\omega }_{a}} = {{\omega }_{s}} + {{\omega }_{d}}$ and ${{\omega }_{a}} = {{\omega }_{s}} - {{\omega }_{d}}$ $({{\omega }_{s}} > {{\omega }_{d}})$, respectively, where ${{\omega }_{d}}$ is a receiver pump mode frequency, ${{{\mathbf{e}}}_{{s(d)}}}({\mathbf{x}})$ and ${{{\mathbf{b}}}_{{s(d)}}}({\mathbf{x}})$ are dimensionless electric and magnetic fields, respectively, for the signal mode (detection pump mode in [23]).

SIGNAL POWER

Here we discuss the signal induced by the axion field for the cavity experimental setups. To be more concrete, by using Eqs. (11) and (14) we can rewrite the amplitude in Eq. (12) in general form

$$G = i{{Q}_{{{\text{rec}}}}}g_{{a\gamma \gamma }}^{2}E_{{\text{0}}}^{{{\text{em}}}}B_{{\text{0}}}^{{{\text{em}}}}B_{{\text{0}}}^{{{\text{rec}}}}\frac{{{{V}_{{{\text{em}}}}}\mathcal{G}}}{\Delta },$$

(18)

where $\Delta$ is typical distance between cavities, and the dimensionless factor $\mathcal{G}$ is given by the following expression

$$\begin{gathered} \mathcal{G} = \int\limits_{{{V}_{{\operatorname{rec} }}}} \frac{{{{d}^{3}}x}}{{{{V}_{{\operatorname{rec} }}}}}\int\limits_{{{V}_{{{\text{em}}}}}} \frac{{{{d}^{3}}{\mathbf{x}}{\kern 1pt} '}}{{{{V}_{{{\text{em}}}}}}}({\mathbf{e}} \cdot {\mathbf{b}})\text{*}{\kern 1pt} ({\mathbf{x}})({\mathbf{e}} \cdot {\mathbf{b}})({\mathbf{x}}{\kern 1pt} ') \\ \times \;\frac{{{{e}^{{i{{k}_{a}}|{\mathbf{x}} - {\mathbf{x}}'|}}}}}{{4\pi }}\frac{\Delta }{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right|}}. \\ \end{gathered} $$

(19)

In the steady regime the averaged signal power can be expressed in the following form,

$${{P}_{{{\text{signal}}}}} = \frac{{{{\omega }_{s}}}}{{{{Q}_{{\operatorname{rec} }}}}}\int\limits_{{{V}_{{\operatorname{rec} }}}} {{d}^{3}}{\mathbf{x}}{{\left\langle {\left| {{\mathbf{E}}_{s}^{2}({\mathbf{x}},t)} \right|} \right\rangle }_{t}} = \frac{{{{\omega }_{s}}}}{{{{Q}_{{\operatorname{rec} }}}}}\frac{1}{2}{{\left| G \right|}^{2}}{{V}_{{\operatorname{rec} }}},$$

(20)

where ${{{\mathbf{E}}}_{s}}({\mathbf{x}},t)$ is a signal solenoidal electric field that is resonantly enhanced by the ALP in the receiver. It is important to note that Eq. (20) implies ${{\left\langle {{{{\left| {{\mathbf{E}}({\mathbf{x}},t)} \right|}}^{2}}} \right\rangle }_{t}}$ = ${{\left\langle {{{{\left| {{\mathbf{B}}({\mathbf{x}},t)} \right|}}^{2}}} \right\rangle }_{t}}$ (see, e.g., [26] and references therein for detail). We imply that time averaging of the squared magnitude results in the replacement ${{\left\langle \ldots \right\rangle }_{t}} \to {\text{1/2}}$ [25]. We note that this approach provides the same result as the power spectral density calculation [23, 27] for the narrow signal bandwidth limit.

We estimate sensitivity numerically as maximum output in the receiver cavity that is given by the Dicke radiometer equation,

$${\text{SNR}} = \frac{{{{P}_{{{\text{signal}}}}}}}{{{{P}_{{{\text{noise}}}}}}}\sqrt {t\Delta \nu } ,$$

(21)

where $t$ is an integration time for a signal, $\Delta \nu$ is its bandwidth and ${{P}_{{{\text{noise}}}}}$ is a power of thermal noise which can be estimated as ${{P}_{{{\text{noise}}}}} \simeq T\Delta \nu$ in the limit ${{\omega }_{s}} \ll T$, where $T \simeq 1.5$ K is the typical temperature of the receiver. We consider two options for $\Delta \nu$: the bandwidth of a cavity mode itself (i.e., $\Delta \nu \simeq {{\nu }_{s}}{\text{/}}{{Q}_{{{\text{rec}}}}}$, where ${{\nu }_{s}} = {{\omega }_{s}}{\text{/}}(2\pi )$) and the narrowest possible bandwidth of a pump generator, which can be as small as $\Delta \nu \simeq {\text{1/}}t$ (see, e.g., [23, 25] and references therein).

It is worth noticing that in the present paper we study only noise from the thermal fluctuation. This implies that the other sources of the background should be significantly mitigated. The latter includes the mechanical noise and oscillator phase noise that has been considered explicitly in [23, 27]. However, we conservatively expect that these backgrounds can be subdominant to the thermal noise by further optimization of the experimental facility.

Finally, by using Eqs. (20) and (21) one can obtain the general formula for the expected sensitivity,

$${{g}_{{a\gamma \gamma }}} = {{\left[ {\frac{{2{{\Delta }^{2}}T{\kern 1pt} SNR}}{{{{\omega }_{s}}{{Q}_{{\operatorname{rec} }}}E_{{{\text{0}}{\text{,em}}}}^{2}B_{{{\text{0}}{\text{,em}}}}^{2}B_{{0,\operatorname{rec} }}^{2}V_{{{\text{em}}}}^{{\text{2}}}{{V}_{{\operatorname{rec} }}}{{{\left| \mathcal{G} \right|}}^{2}}}}} \right]}^{{\frac{1}{4}}}}{{\left( {\frac{{\Delta \nu }}{t}} \right)}^{{\frac{1}{8}}}},$$

(22)

which is valid for estimation of the ALP expected limit (${\text{SNR}} \simeq 5$) for all benchmark setups considered in the next section.

EXPECTED REACH

Now we compare the efficiencies of four different experimental setups for probing ALPs with LSW methods: (i) MF (RF) emitter + M*F (RF) receiver; (ii) MM (SRF) emitter + M*M (SRF) receiver; (iii) MM (SRF) emitter + M*F (RF) receiver; (iv) MF (RF) emitter + M*M (SRF) receiver (for details see, e.g., Fig. 2). In addition, we study in detail the sensitivity dependence on the spatial geometry (relative position of emitter and receiver cylindrical cavities) and radius to length ratio $R{\text{/}}L$ of the ALP emitter for these benchmark experimental proposals.

Fig. 2.

Four general types of the experimental proposals.

MF EMITTER + M*F RECEIVER

At first let us consider the typical LSW setup consisting of two RF cavities which are placed both into a strong static magnetic field [14]. The experimental realization of that idea was carried out by the CROWS experiment [20]. We show the sensitivity of this type of experiment for the characteristic volume of the emitter and receiver cavities ${{V}_{{\operatorname{rec} }}} = {{V}_{{{\text{em}}}}} \simeq 1$ m³, the receiver quality factor³${{Q}_{{{\text{rec}}}}} \simeq {{10}^{5}}$.

We consider the characteristic magnitude of the emitter pump mode $E_{{\text{0}}}^{{{\text{em}}}}$ = 3 MV/m ($B_{{\text{0}}}^{{{\text{em}}}}$ = 0.01 T). It is worth noticing that the emitter quality factor ${{Q}_{{{\text{em}}}}}$ can be smaller by several times [29] than the receiver quality factor ${{Q}_{{\operatorname{rec} }}} \simeq {{10}^{5}}$ due to the high power of the pump mode. Given the volume and quality factor, the emitter power is of the order of ${{P}_{{{\text{em}}}}} \sim 100$ kW. The latter to be a reasonable power for injection in the emitter. The typical value of the static magnetic field are taken as $B_{{\text{0}}}^{{{\text{em}}}} = B_{0}^{{\operatorname{rec} }}$ = 3 T in Fig. 3. The distance between receiver and emitter walls is $\Delta = 0.5$ m. The pump mode of the emitter and the signal mode of the receiver are TM₀₁₀.

Fig. 3.

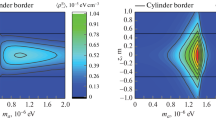
(Color online) Sensitivity of MF emitter + M*F receiver setup for both coaxial and parallel cavity locations and the TM₀₁₀ emitter and receiver modes. Left panel: the dependence on the emitter cavity radius-to-length ratio $R{\text{/}}L$ for the typical volume ${{V}_{{{\text{em}}}}} = 1$ m³. Right panel: expected reach as a function of ALPs mass at optimal $R{\text{/}}L$ for coaxial ($R{\text{/}}L \simeq 1.67$, $R \simeq 0.81\;{\kern 1pt} {\text{m}}$, $L \simeq 0.49$ m) and parallel ($R{\text{/}}L \simeq 0.37$, $R \simeq 0.49\;{\kern 1pt} {\text{m}}$, $L \simeq 1.32$ m) geometries. The distance between cavity walls is $\Delta = 0.5$ m, the cavity volumes are ${{V}_{{\operatorname{rec} }}} = {{V}_{{{\text{em}}}}} = 1$ m³. The integration time is $t = {{10}^{6}}$ s. The temperature of the receiver is taken as $T = 1.5$ K.

In Fig. 3 (left panel) we show the expected sensitivity of the setup as a function of $R{\text{/}}L$ for both parallel and coaxial designs of the cavities (see, e.g., Fig. 1 for detail), we also set the ALP benchmark masses to be ${{m}_{a}} = 0$ and ${{m}_{a}} \simeq {{\omega }_{a}}$. We take into account that the ${{Q}_{{{\text{rec}}}}}$ depends on the chosen mode and cavity geometry, ${{Q}_{{\operatorname{rec} }}}$ = ${{\omega }_{s}}{\text{/}}{{R}_{s}}{{V}_{{\operatorname{rec} }}}{\text{/}}{{S}_{{\operatorname{rec} }}}$ ∝ $\sqrt {{{\omega }_{s}}} {{V}_{{\operatorname{rec} }}}{\text{/}}{{S}_{{\operatorname{rec} }}}$, where ${{R}_{s}}$ is the surface resistance and ${{S}_{{{\text{rec}}}}}$ is the surface area of the detector cavity [30], here we also set the value ${{Q}_{{\operatorname{rec} }}} = {{10}^{5}}$ for $R{\text{/}}L = 1$. We consider sensitivity for ${{m}_{a}} = 0$ as the most important setup characteristic compared to the resonant bound at ${{m}_{a}} = {{\omega }_{s}}$ regime throughout the paper. It implies that the typical bounds at ${{m}_{a}} = 0$ cover the larger logarithmic mass scale range (${{m}_{a}} \lesssim {{\omega }_{a}}{\text{/}}2$) in $({{g}_{{a\gamma \gamma }}},{{m}_{a}})$ plane. It turns out that coaxial design for $R{\text{/}}L \gtrsim 1$ is more preferable. It is remarkable that in this case the typical expected reaches for both masses ${{m}_{a}} = 0$ and ${{m}_{a}} \simeq {{\omega }_{a}}$ coincide by the order of the magnitude at the level of ${{g}_{{a\gamma \gamma }}} \simeq 3 \times {{10}^{{ - 11}}}$ GeV^–1. However, there is a notable difference between the expected reaches at ${{m}_{a}} = 0$ and ${{m}_{a}} \simeq {{\omega }_{s}}$ for the parallel design. Note that optimal radius to length ratio (that implies better sensitivity on ${{g}_{{a\gamma \gamma }}}$ in case of ${{m}_{a}} = 0$) is $R{\text{/}}L \simeq 1.67$ for coaxial design and $R{\text{/}}L \simeq 0.37$ for parallel design.

In Fig. 3 (right panel) we show the expected reach as a function of the ALP mass ${{m}_{a}}$ for both coaxial and parallel locations of the cavities at the optimal ratios $R{\text{/}}L$ assuming two options of the signal bandwidth $\Delta \nu \simeq \nu {\text{/}}{{Q}_{{{\text{rec}}}}}$ and $\Delta \nu \simeq 1{\text{/}}t$, where $t \simeq {{10}^{6}}$ s is the typical time of measurement. The conservative cavity bandwidth $\Delta \nu \simeq \nu {\text{/}}{{Q}_{{{\text{rec}}}}}$ yields the expected limit ${{g}_{{a\gamma \gamma }}} \lesssim 5 \times {{10}^{{ - 10}}}$ GeV^–1 that is weaker than the CAST constraint [9]. However, the optimistic bandwidth $\Delta \nu \simeq 1{\text{/}}t$ can provide the expected reach ${{g}_{{a\gamma \gamma }}} \lesssim 3 \times {{10}^{{ - 11}}}$ GeV^–1 for ${{m}_{a}} \lesssim {{\omega }_{a}}{\text{/}}2$.

It is worth noting that corresponding heat production makes it challenging to keep the emitter temperature at a required level. On the other hand, relatively small temperatures $T \lesssim 1$ K are required for the receiver cavity in order to avoid the problem of thermal noise. So that keeping two cavities at different temperatures would require a development of sophisticated RF methods for the regarding setup.

MM EMITTER + M*M RECEIVER

The second setup of our interest consists of two equal SRF cavities [23]. In the emitter cavity, ALPs are generated by an interaction of two cavity modes. In the detection cavity, produced ALPs interact with a single pump mode (which coincides with one of the production cavity pump modes), producing the resonantly enhanced signal mode in the receiver cavity. The magnitude of the surface amplitude of pump modes for an SRF cavity to be as small as $B_{{\text{0}}}^{{{\text{em}}{\text{,rec}}}} \lesssim 0.1$ T ($E_{{\text{0}}}^{{{\text{em}}{\text{,rec}}}} \lesssim 30$ mV/m) to avoid the superconductivity state destruction. The volume of the emitter and receiver cavities ${{V}_{{\operatorname{rec} }}} = {{V}_{{{\text{em}}}}} \simeq 1$ m³, their quality factor $Q \simeq {{10}^{{10}}}$. This high quality factor implies specific fine tuning of the emitter cavity frequency, see [31]. The expected power of the emitter cavity is ${{P}_{{{\text{em}}}}} \simeq 0.1$ kW. In Fig. 4 the typical sensitivities for the regarding LSW setup are presented.

Fig. 4.

(Color online) Sensitivity of MM emitter + M*M receiver cavity setup. This facility implies combination of TM₀₁₀ + TE₀₁₁ production pump modes. The pump mode of a receiver and its signal mode are chosen to be TM₀₁₀ and TE₀₁₁, respectively. The case of ALPs frequency ${{\omega }_{a}} = {{\omega }_{ + }}$ is considered. Left panel: the expected limit ${{g}_{{a\gamma \gamma }}}$ as a function of production cavity radius-to-length ratio $R{\text{/}}L$ (we set the emitter volume at ${{V}_{{{\text{em}}}}} = 1$ m³). Right panel: Sensitivity as a function of ALPs mass at optimal $R{\text{/}}L$ for coaxial ($R{\text{/}}L \simeq 1.60$, $R \simeq 0.80$ m, $L \simeq 0.50$ m) and parallel ($R{\text{/}}L \simeq 0.35$, $R \simeq 0.48$ m, $L \simeq 1.37$ m) designs. The distance between cavity walls is $\Delta = 0.5$ m, the volume of each cavity is ${{V}_{{{\text{em}}}}} = {{V}_{{\operatorname{rec} }}} = 1$ m³. ${{Q}_{{\operatorname{rec} }}} = {{10}^{{10}}}$. Integration time is $t = {{10}^{6}}$ s. The temperature of the receiver is taken as $T = 1.5$ K.

In Fig. 4 (left panel) the expected reach as function of emitter radius-to-length ratio $R{\text{/}}L$ is shown. As in previous case, we take into account the dependence of the quality factor $Q$ on cavity geometry which reads ${{Q}_{{\operatorname{rec} }}}$ = ${{\omega }_{s}}{\text{/}}{{R}_{s}}{{V}_{{\operatorname{rec} }}}{\text{/}}{{S}_{{\operatorname{rec} }}}$ ∝ $\omega _{s}^{{ - 1}}{{V}_{{\operatorname{rec} }}}{\text{/}}{{S}_{{\operatorname{rec} }}}$ for SRF cavity [32], and fix the value as ${{Q}_{{\operatorname{rec} }}} = {{10}^{{10}}}$ for $R{\text{/}}L = 1$. It turns out that the optimal magnitude of $R{\text{/}}L$ for the coaxial cavity location and for the ALP mass limit ${{m}_{a}} = 0$ is $R{\text{/}}L \simeq 1.6$. The regarding expected sensitivity is ${{g}_{{a\gamma \gamma }}} \lesssim 5 \times {{10}^{{ - 11}}}$ GeV^–1 that is comparable with the CAST bound ${{g}_{{a\gamma \gamma }}} \lesssim 6 \times {{10}^{{ - 11}}}$ GeV^–1. For parallel location of the cavities, the optimal radius-to-length ratio is $R{\text{/}}L \simeq 0.35$ implying ${{m}_{a}} = 0$. We note that zero axion mass bounds ${{g}_{{a\gamma \gamma }}} \lesssim 6 \times {{10}^{{ - 10}}}$ GeV^–1 are ruled out by the CAST. The signal cavity bandwidth is chosen to be at the level $\Delta \nu \simeq {\text{1/}}t$, where $t \simeq {{10}^{6}}$ s is a typical time of the measurements.

In Fig. 4 (right panel) we show the expected limit ${{g}_{{a\gamma \gamma }}}$ of this setup as a function of the ALP mass ${{m}_{a}}$. It turns out that the sensitivity has a sharp peak at the resonance ${{m}_{a}} \simeq {{\omega }_{a}}$ for both coaxial and parallel designs. For the optimistic signal bandwidth $\Delta \nu \simeq 1/t$ regarding expected limit is estimated at the level of ${{g}_{{a\gamma \gamma }}} \lesssim 5 \times {{10}^{{ - 11}}}$ GeV^–1 for ${{m}_{a}} \lesssim {{\omega }_{a}}{\text{/2}}$.

The detection of a relatively small signal in a cavity with high intensity pump mode may lead to challenging technical issues, mainly related to filtering of the tiny signal mode from the very intensive pump mode. To resolve this issue, one may consider a “bottle-shape” cavity geometry similar to that discussed in [25].

MM EMITTER + M*F RECEIVER

The next setup that we consider in our study consists of a production SRF cavity with two pump modes and a detection RF cavity immersed into static magnetic field [24, 33].

In Fig. 5 we show the sensitivity of this type of experiment for the characteristic volume of the emitter cavity ${{V}_{{{\text{em}}}}} \simeq 1$ m³ and its quality factor ${{Q}_{{{\text{em}}}}} \simeq {{10}^{{10}}}$. Amplitudes of the emitter pump modes are $B_{{\text{0}}}^{{{\text{em}}}} =$ 0.1 T ($E_{{\text{0}}}^{{{\text{em}}}} = 30$ MV/m) to avoid destruction of the superconducting state. The expected power of the emitter cavity is ${{P}_{{{\text{em}}}}} \simeq 0.1$ kW. The distance between receiver and emitter walls is $\Delta = 0.5$ m. The pump modes of the emitter are TM₀₁₀ and TE₀₁₁, and the signal mode of the receiver is TM₀₁₀. Note that the receiver must be smaller than the emitter for the frequency equality ${{\omega }_{1}} + {{\omega }_{2}} = {{\omega }_{s}}$ to be fulfilled. The receiver quality factor is ${{Q}_{{\operatorname{rec} }}} \simeq {{10}^{5}}$ and the typical value of the static magnetic field $B_{{\text{0}}}^{{{\text{rec}}}} = 3$ T.

Fig. 5.

(Color online) Sensitivity of the MM emitter + M*F receiver setup for TM₀₁₀ + TE₀₁₁ emitter pump modes and TM₀₁₀ detection signal mode. The case of ALPs frequency ${{\omega }_{a}} = {{\omega }_{ + }}$ is considered. Left panel: the sensitivity dependence on emitter cavity radius-to-length ratio $R{\text{/}}L$ (fixed volume of ${{V}_{{{\text{em}}}}} = 1$ m³ and fixed length of ${{L}_{{\operatorname{rec} }}} = 0.5$ m). Right panel: sensitivity as a function of ALPs mass at optimal $R{\text{/}}L$ for coaxial ($R{\text{/}}L \simeq 1.44$, $R \simeq 0.77$ m, $L \simeq 0.54$ m, ${{R}_{{{\text{rec}}}}} \simeq 0.22$ m, ${{L}_{{{\text{rec}}}}} \simeq 0.5$ m) and parallel ($R{\text{/}}L \simeq 0.33$, $R \simeq 0.47$ m, $L \simeq 1.43$ m, ${{R}_{{\operatorname{rec} }}} \simeq 0.18$ m, ${{L}_{{{\text{rec}}}}} \simeq 0.5$ m) design. The distance between cavity walls is $\Delta = 0.5$ m, the volume of the emitter cavity is ${{V}_{{{\text{em}}}}} = 1$ m³. Integration time is $t{{ = 10}^{6}}$ s. The temperature of the receiver is taken as $T = 1.5$ K.

In Fig. 5 (left panel) we show the typical expected reach for this setup as a function of $R{\text{/}}L$ for the emitter cavity. We emphasize that the regarding bounds are  ruled out by the CAST facility at ${{g}_{{a\gamma \gamma }}} \lesssim 3.0 \times$ 10^‒10 GeV^–1. This can be also justified from the right panel of Fig. 5 where the typical bounds are shown in the $({{g}_{{a\gamma \gamma }}},{{m}_{a}})$ plane.

MF EMITTER + M*M RECEIVER

The final setup consists of a production RF cavity with a pump mode into static magnetic field and a detection SRF cavity with a pump mode.

In Fig. 6 we show the sensitivity of this type of experiment for the characteristic volume of the receiver cavity ${{V}_{{{\text{rec}}}}} \simeq 1$ m³ and its quality factor ${{Q}_{{{\text{rec}}}}} \simeq {{10}^{{10}}}$. The amplitude of the emitter pump mode is $E_{{\text{0}}}^{{{\text{em}}}} = 3$ MV/m ($B_{0}^{{{\text{em}}}} = 0.01$ T), the magnitude of static magnetic field if ${{B}_{{\operatorname{ext} }}} = 3$ T. The expected power of the emitter cavity is ${{P}_{{{\text{em}}}}} \sim 100$ kW. The distance between receiver and emitter walls is $\Delta = 0.5$ m. The pump mode of the emitter is TM₀₁₀, the pump mode of the receiver is TM₀₁₀ and the signal mode of the receiver is TE₀₁₁. Note that the emitter must be smaller than the receiver for the frequency equality ${{\omega }_{1}} + {{\omega }_{2}} = {{\omega }_{{{\text{em}}}}}$ to be fulfilled. The receiver quality factor is ${{Q}_{{{\text{rec}}}}} \simeq {{10}^{{10}}}$ and the typical value of the pump mode amplitude is $B_{0}^{{\operatorname{rec} }} = 0.1$ T.

Fig. 6.

(Color online) Sensitivity of the MF emitter + M*M receiver setup for TM₀₁₀ emitter pump mode and TM₀₁₀ receiver pump mode and TE₀₁₁ receiver signal mode. Left panel: the sensitivity dependence on receiver cavity radius-to-length ratio $R{\text{/}}L$ (fixed volume of ${{V}_{{\operatorname{rec} }}} = 1$ m³ and fixed length of ${{L}_{{{\text{em}}}}} = 0.5$ m). Right panel: sensitivity as a function of ALPs mass at optimal $R{\text{/}}L$ for coaxial ($R{\text{/}}L \simeq 1.46$, $R \simeq 0.78$ m, $L \simeq 0.53$ m, ${{R}_{{{\text{em}}}}} \simeq 0.22$ m, ${{L}_{{{\text{em}}}}} \simeq 0.5$ m) and parallel ($R{\text{/}}L \simeq 0.36$, $R \simeq 0.49$ m, $L \simeq 1.35$ m, ${{R}_{{{\text{em}}}}} \simeq 0.18$ m, ${{L}_{{{\text{em}}}}} \simeq 0.5$ m) design. The distance between cavity walls is $\Delta = 0.5$ m, the volume of the receiver cavity is ${{V}_{{\operatorname{rec} }}} = 1$ m³. Integration time is $t = {{10}^{6}}$ s. The temperature of the receiver is taken as $T = 1.5$ K.

In Fig. 6 (left panel) we show the typical expected reach for this setup as a function of $R{\text{/}}L$ for the receiver cavity. We emphasize that the regarding bounds are ruled out by the CAST facility at ${{g}_{{a\gamma \gamma }}} \lesssim 9.0 \times {{10}^{{ - 11}}}$ GeV^–1 for the mass range ${{m}_{a}} \lesssim {{\omega }_{a}}{\text{/2}}$. This can be also justified from the right panel of Fig. 6 where the typical bounds are shown in the $({{g}_{{a\gamma \gamma }}},{{m}_{a}})$ plane. Remarkably however that the typical peak bounds at ${{m}_{a}} \simeq 2 \times {{10}^{{ - 6}}}$ eV can rule out the CAST limits.

RESULTS AND DISCUSSION

We compared four types of the LSW radio setups for ALP searches and determined the best design for them. We summarize our study presenting important parameters for each setup in Table 1.

Table 1. Comparison of the characteristics for various experimental setups. The geometrical formfactor $\left| \mathcal{G} \right|$ and the setup sensitivity ${{g}_{{a\gamma \gamma }}}$ are presented for the best ratio of $R{\text{/}}L$ of coaxial location and the mass of ALPs ${{m}_{a}} \lesssim {{\omega }_{a}}{\text{/2}}$

We concluded that the MF emitter + M*F receiver and the MM emitter + M*M receiver setups can achieve the similar top sensitivity ${{g}_{{a\gamma \gamma }}} \lesssim (3{-} 5) \times$ 10^‒11 GeV^–1 at ${{m}_{a}} \lesssim {{\omega }_{a}}{\text{/}}2$. In particular, it turns out that the larger electromagnetic field combination and the geometrical formfactor of RF cavities compensate its smaller quality factor.

Moreover, we find that the best relative location of the cavities is coaxial with the ratio of $R{\text{/}}L \simeq 1.6$.

The MF emitter + M*F receiver setup is a modification of the CROWS experiment [20] that implies larger volume of the cavities ${{V}_{{{\text{em}}}}} \simeq {{V}_{{{\text{rec}}}}} \simeq 1$ m³, lower temperature, and narrower bandwidth of the signal, $\Delta \nu \simeq {\text{1/}}t$. However, there is a disadvantage of this setup that implies the relatively large emitter power ${{P}_{{{\text{em}}}}} \sim 100$ kW.

The advantage of the MM emitter + M*M receiver setup is that its emitter power is 4 orders of magnitude smaller than the previous one. However, in this case the main technical challenges would be related to the signal mode filtering from the pump mode and fine tuning of cavity gabarites.

Given the benchmark parameters, the last two setups, MM emitter + M*F receiver and MF emitter + M*M receiver, has the weakest sensitivity, see Table 1. Moreover, the typical bounds ${{g}_{{a\gamma \gamma }}} \lesssim \mathcal{O}{{(10}^{{ - 10}}})$ GeV^–1 would be ruled out by the CAST. Also, there is a disadvantage of these proposals. In particular, the condition ${{\omega }_{1}} + {{\omega }_{2}} = {{\omega }_{s}}$ implies the specific type of the emitter modes, the latter is linked to the sizes of the cavity. Moreover, the modification of the pump modes would require the changing of the receiver geometry. The disadvantages of the MF emitter + M*M receiver include also technical difficulties of the first two setups.