Magnetic Anisotropy of Single-Ion Magnet (PPh₄)₂ [ReF₆]·2H₂O

Studying of single-molecule magnets has sprung many surprises such as, e.g., quantum tunneling of the magnetization, which is strongly related to the presence of a magnetic anisotropy. Electron spin resonance and inelastic neutron scattering measurements of (PPh₄)₂[ReF₆]⋅2H₂O complex evidence an unprecedented large single-site magnetic anisotropy of $D \sim 35$ K in this material. Using state-of-the-art ab initio calculations we found that the single-ion anisotropy is indeed very large (but does not exceed 12 K) and revealed the physical mechanism lying behind this phenomenon.

INTRODUCTION

Nowadays, there is a need to store and process an increasing amount of data, so the issue of developing faster and more voluminous storage media is especially acute. Thanks to advances in the field of spintronics, devices have been developed in which electron spins and spin currents can be manipulated by an external magnetic field or effective fields caused by spin–orbit interaction [1, 2].

At present, the main materials for manufacturing spintronic devices are magnetic metals/semiconductors and topological insulators. However, an alternative class of organometallic compounds called single-molecule magnets (SMM) [3, 4] have been under study since 1990s. Magnetic moments within these molecules are carried by magnetically active centers, containing one (so-called single-ion magnets, SIM) or more transition metal ions. The advantages of such magnets are their light weight due to the organic component and slow relaxation. Moreover, these materials can be used in quantum computing [5].

A hexafluoride unit [ReF₆]^2– in (PPh₄)₂[ReF₆]⋅2H₂O, (1), (PPh₄ stands for tetraphenylphosphonium, (C₆H₅)₄P), was found to demonstrate SMM behavior below 4 K: application of a small dc field causes a slow dynamics of the magnetization [6]. One of the key characteristics describing the spin system in SMM is the single-ion anisotropy (SIA). This parameter was estimated to be very large, $D =$ 34 K, for (1), see Eq. (1) below. Positive sign of D indicates an easy-plane-type anisotropy [6]. Interestingly, a sister material based on adding 1-vinylimidazole (viz) to a methanol solution of [ReF₆]^2– and Zn²⁺ chains with alternating metal centers, [Zn(viz)₄(ReF₆)], (2), preserves slow dynamics, but inelastic neutron scattering was unable to estimate D in this compound, while temperature dependence of magnetic susceptibility in (1) and (2) is very similar [6].

In both these systems Re is 4+ and it corresponds to the $5{{d}^{3}}$ electronic configuration with half-filled ${{t}_{{2g}}}$ subshell. One might expect the orbital moment to be quenched, and the spin–orbit coupling to be ineffective [7], and hence, the single-ion anisotropy to be small [8]. This inconsistency was a motivation for the present studies. Using state-of-art density functional theory (DFT) calculations we investigated the total energy dependence on spin direction and calculated single-ion anisotropy in both (PPh₄)₂[ReF₆]⋅2H₂O and [Zn(viz)₄(ReF₆)]. We obtained that both compounds have a large easy-plane anisotropy and found that it is related to a particular type of distortion of ReF₆ octahedra (elongation) with strong ${{t}_{{2g}}} - {{e}_{g}}$ crystal-field splitting, and that spin–orbit coupling is involved in the unquenching of the orbital moment.

DETAILS OF THE CALCULATION

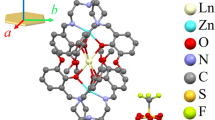
Structural models for the electronic structure calculations were taken from [6] and are shown in Figs. 1, 2. It is worth noting that the space group in (1) is ${\text{P}}\overline 1$, which indicates the presence of an inversion center in the cell. [ReF₆]^2– are irregular tilted octahedra with a predominantly axial distortion. It is interesting whether this is due to a specific surrounding (bonding geometry) or it is related to the activation of the Jahn–Teller effect by the spin–orbit coupling [9, 10]. In (2) the space group is P4₂/n and ReF₆ octahedra are more symmetrical but are still tilted and have an axial elongation.

Fig. 1.

(Color online) Crystal structure of (a) (PPh₄)₂[ReF₆]⋅2H₂O unit cell, (b) first and second octahedra with arrows which show how F atoms transform due to presence of the inversion center between these atoms. Metal–ligand bond lengths [Å] for ReF₆: Re–F_ax 1.96696–1.97198, Re–F_eq 1.95144–1.95774; selected ligand–metal–ligand angles: F_i–Re–F_j = 88.5416°–91.858°.

Fig. 2.

(Color online) Crystal structure of (a) [Zn(viz)₄(ReF₆)] unit cell, (b) chain links of Re (yellow-gray) and Zn (gray) located inside octahedra with labeled atoms. Selected bond lengths [Å] for ReF₆: Re–F_ax (along the c axis) = 1.96485, Re–F_eq (ab plane) = 1.95051; selected ligand–metal–ligand angles: F_i–Re–F_j = 89.7834°–90.2166°.

All calculations were performed using the VASP code [11–14] with projector-augmented wave method (PAW) [15], employing Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) exchange-correlation functional [16]. For the Brillouin zone integration, a 2 × 2 × 1 Monkhorst–Pack mesh was used. The cutoff energy for the plane-wave basis was set to 480 eV. Stopping criterion for the electronic self-consistency steps was selected as 10^–7 eV. Ionic relaxation was not carried out.

We took into account strong Coulomb correlations $via$ rotationally invariant DFT + U approach after Dudarev et al. [17]. For Re atoms, values of the onsite Coulomb repulsion and Hund’s exchange were chosen to be 1.5 and 0.5 eV, respectively [18]. Specified Wigner–Seitz radii for rhenium, zinc, fluorine, nitrogen, oxygen, hydrogen, phosphorus, and carbon are 1.434, 1.270, 0.794, 0.741, 0.820, 0.370, 1.233, and 0.863 Å, respectively.

In magnetic calculations with the spin–orbit coupling (GGA + U + SOC) the constrained local moments approach was used; i.e., the direction of the magnetic moments were constrained to lie along particular bonds. The total energies of different configurations were calculated and mapped onto a spin Hamiltonian.

RESULTS AND DISCUSSION

We start with the discussion of the electronic structure. The results of GGA + U calculations for (PPh₄)₂[ReF₆]·2H₂O are presented in Fig. 3. Since rhenium is in an octahedral field, the $5d$ levels split onto ${{t}_{{2g}}}$ and ${{e}_{g}}$ subshells with three and two orbitals, respectively. It is clear that peaks in the partial density of states just below the Fermi level correspond to the half-filled rhenium ${{t}_{{2g}}}$ subshell hybridized with fluorine p states. The constructed partial charge density for the d state of rhenium over the energy interval from ‒0.5 to –0.1 eV presented in Fig. 4 shows a symmetrical shape—the sum of three ${{t}_{{2g}}}$ orbitals, whose lobes lie in the space between the axes directed from Re to the fluorine ligands. As shown in Fig. 3, valent carbon p states are located right between filled and unoccupied ${{t}_{{2g}}}$ Re states. Partial density of states plot corresponding to the valent ${{e}_{g}}$ subshell is more than 4 eV away from the occupied half of ${{t}_{{2g}}}$ (that is above Fermi level). The group of the F-$2p$ states lies at lower energies and, therefore, is not shown in the plot.

Fig. 3.

(Color online) Total (black), partial rhenium 5$d$ (blue), fluorine 2$p$ (violet) and other partial density of states plots in the GGA + U calculations with the Fermi level shifted to zero. The width of the smearing for integration was taking to be 0.05 eV. Spin-up and spin-down plots are identical to each other.

Fig. 4.

(Color online) Charge density for the first (a) and the second (b) octahedron corresponding to occupied ${{t}_{{2g}}}$ bands (just below the Fermi level, from –1.5 to 0 eV) in the GGA + U calculation.

Taking into account the on-site Coulomb repulsion and in fact Stoner exchange splitting results in formation of the gap of ~0.5 eV at the Fermi level.

The magnetic moment on Re in GGA + U calculations for the [PPh₄]⁺ salt, (1), and the Zn^II chain, (2), was found to be 2.78 ${{\mu }_{{\text{B}}}}$. It is slightly less than one would expect for $5{{d}^{3}}$ electronic configuration. This small deviation is very typical for the DFT calculations, see, e.g., [19–22], and can be explained by covalency (hybridization) effects. In case of Zn(viz)₄(ReF₆), Zn^II has fully occupied d state and should not affect magnetic properties.

As one can see from Tables 1 and 2, taking into account the spin–orbit coupling via GGA + U + SOC approach not only decreases spin moment, but also results in formation of a low orbital moment.

Table 1. Results of GGA + U + SOC calculations for (PPh₄)₂[ReF₆]·2H₂O: spin directions are collinear to the bond vectors from a metal ion to a ligand shown in the first column; $\Delta E$ corresponds to the total energy difference per Re atom between given configuration and configuration with the lowest energy. For atom numeration see Fig. 1

Table 2. Results of GGA + U + SOC calculations for Zn(viz)₄(ReF₆): spin directions are collinear to the bond vectors from a metal ion to a ligand shown in the first column; $\Delta E$ correspond to the total energy difference per Re atom between given configuration and configuration with the lowest energy. For atom numeration see Fig. 2

In order to estimate single-ion anisotropy we performed total energy GGA + U + SOC calculations for different spin directions and mapped these results onto the model, where the SIA is described by the following Hamiltonian:

$${{\hat {H}}_{{{\text{SIA}}}}} = D\hat {S}_{z}^{2},$$

(1)

where positive D corresponds to the easy-plane type of anisotropy, while negative to the easy-axis type. It is worth mentioning that one needs to use antiferromagnetic arrangement of magnetic moments of two Re atoms in the unit cell. Such a choice is based on the presence of the inversion center and octahedral tilting. It results in a situation, in which spins are not directed along the metal–ligand bonds simultaneously for both octahedra in case of ferromagnetic order. This may lead to an inaccurate estimation of the single-ion anisotropy parameter.

The results for both compounds are presented in Tables 1 and 2. As one can see, the lowest energies correspond to those solutions, in which spins are confined in the basal plane of Re octahedra, and, therefore, to the easy-plane magnetic anisotropy. Direct calculations for $S = 3{\text{/}}2$ in (1) yielded $D = 11.7$ K, while for (2) D parameter equals to 16.8 K.

Strong single-ion anisotropy is usually associated with substantial orbital contribution to the total magnetic moment [8]. It is rather surprising that the orbital moment is unquenched in our calculations (see Tables 1 and 2), because the ${{t}_{{2g}}}$ subshell, characterized by the effective orbital moment $\tilde {l} = 1$ [7, 23], is half-filled and, therefore, $\langle {{\hat {\tilde {l}}}_{z}}\rangle$ should be zero. The reason for this phenomenon can be the admixture of the higher lying ${{e}_{g}}$ to ${{t}_{{2g}}}$ states due to low symmetry of the crystal field (${{C}_{1}}$ point group), that can unquench the orbital moment and result in substantial single-ion anisotropy, and strong spin–orbit coupling having off-diagonal elements between ${{t}_{{2g}}} - {{e}_{g}}$ orbitals [24].

In order to estimate the crystal-field splitting we performed projection of the DFT Hamiltonian onto the basis defined by optimized projected localized orbitals [25] in the nonmagnetic DFT calculations (to avoid any splitting due to magnetism or correlation effects). The results are summarized in Fig. 5. The splitting of the Re ${{t}_{{2g}}}$ sub-shell in the DFT approach is about ~40 meV, with the doublet of xz, yz orbitals lying below the xy singlet (in the local coordinate system with the axes directed from Re towards fluorine atoms, z direction is to the apical ligands). One can see that the ${{t}_{{2g}}} - {{e}_{g}}$ crystal-field splitting ($10Dq$ in spectroscopy) in (PPh₄)₂[ReF₆]⋅2H₂O is of the order of 3.5 eV. This value is typical for the crystal-field splitting in the inorganic transition metal compounds (~3–4 eV for $5d$ oxides) [23].

Fig. 5.

Results of the Wannier function projection of the nonmagnetic DFT Hamiltonian for (1). We used the local coordinate system where axes are directed as much as possible to the ligand to calculate on-site energies of different Re $5d$ orbitals.

One can also estimate the magnetic anisotropy using these values of the crystal-field splitting. The ground state of ${{d}^{3}}$ configuration in presence of a substantial ${{t}_{{2g}}} - {{e}_{g}}$ splitting is the orbital singlet ${{\Gamma }_{2}}$ (and spin quartet because $S = 3{\text{/}}2$). Since symmetry of the crystal-field is lower than cubic, ${{t}_{{2g}}}$ levels get split onto nearly degenerate xz and yz orbitals, which are lower in energy than xy orbital (see Fig. 5). The spin–orbit coupling mixes the ground state singlet ${{\Gamma }_{2}}$ with orbital triplet ${{\Gamma }_{5}}$, lying on $10Dq$ higher [7]. This triplet is split by the non-cubic crystal-field onto a doublet, characterized by fictitious orbital moment ${{\tilde {l}}_{z}} = \pm 1$ and having energy ${{\Delta }_{1}}$, and a singlet with ${{\tilde {l}}_{z}} = 0$ and ${{\Delta }_{0}}$.

In the second order of the perturbation theory one can take into account the mixing of these ${{\Gamma }_{5}}$ states with the ground state (${{\Gamma }_{2}}$) due to the spin–orbit coupling. This admixture splits the ground state into two spin doublets and the value of this splitting is proportional to the spin–orbit coupling constant λ [7]:

$$2D = - \frac{{8{{\lambda }^{2}}}}{{{{\Delta }_{0}}}} + \frac{{8{{\lambda }^{2}}}}{{{{\Delta }_{1}}}}.$$

(2)

Since for elongated octahedron ${{\Delta }_{1}} < {{\Delta }_{0}}$, the single-ion anisotropy should be of easy-plane type ($D > 0$), exactly as it is in our GGA + U + SOC calculations. Moreover, using estimation of $\lambda = 320$ meV for Re⁴⁺ [26] and the crystal-field splittings shown in Fig. 5 for (PPh₄)₂[ReF₆]⋅2H₂O, even such an oversimplified consideration (note in passing that there can be important third order corrections in case of strong trigonal field, see [7]) gives a reasonable estimation of $D = 14.6$ K. This agrees with the direct total energy GGA + U + SOC calculations of the single-ion anisotropy presented above.

It is interesting to compare our results with the analysis of the experimental measurements presented in [6]. Fitting temperature and field dependencies of the magnetic susceptibility yields $D = 40$ K. Inelastic neutron experiments detect a peak at 69.1 K (48 cm^–1), which can be attributed to the excitation across a spin gap due to the single-ion magnetic anisotropy and D was estimated to be 34 K (taking into account the results of the electron spin resonance measurement fixing rhombic anisotropy) [6]. Both these estimates look unexpected for Re⁴⁺ ion with ${{d}^{3}}$ electronic configuration and nearly quenched orbital moment. They also strongly differ from our present results (GGA and GGA + U + SOC), that are consistent with each other. It has to be mentioned that in (PPh₄)₂[ReF₆]⋅2H₄O magnetization saturates only at contestable M ~ 1.5μ_B (i.e., nearly half of what one might expect for the ${{d}^{3}}$ configuration) suggesting that account of so-called paraprocesses is important for interpretation of magnetic measurements on powder. It would be useful to recheck available crystal structure data and study electronic structure of (PPh₄)₂[ReF₆]⋅2H₂O using X-ray spectroscopy (e.g., X-ray absorption) to resolve present discrepancy between magnetic measurements, inelastic scattering data and the results of DFT calculations.

CONCLUSIONS

In this work we used ab initio DFT calculations to study the magnetic anisotropy of (PPh₄)₂[ReF₆]⋅2H₂O and based on the same [ReF₆]^2– anion [Zn(viz)₄(ReF₆)] with similar magnetic properties. It was found that both compounds have the easy-plane anisotropy and the corresponding single-ion anisotropy parameters D are equal to 11.7 and 16.8 K. Magnetic moments for both complexes are slightly less than expected 3μ_B due to the covalency effects and substantial spin–orbit coupling. Thus, our results question the interpretation of inelastic neutron scattering spectra. The presence of a nonzero orbital moment is interpreted as due to an admixture of the ${{\Gamma }_{5}}$ states to the ${{\Gamma }_{2}}$ ground state due to the spin–orbit coupling.