Quantization of the Energy Spectrum of Holes in the Adiabatic Potential of the Electron

The spectra of the interband absorption of microscopic CdS crystals, 15 to 30 Å in size, grown in a transparent insulating matrix, are analyzed. A structural feature caused by quantization of the energy spectrum of the hole in the adiabatic potential of its Coulomb interaction with the electron has been detected near the transitions to the lower level of the size quantization of the electron.

Several years ago, a technique was developed for growing microscopic semiconductor crystals in the bulk of a transparent insulating glass matrix, in which their size can be varied directionally over a broad range from several tens to several thousands of angstroms [1, 2]. Quantum size effects in the energy spectrum of excitons [3, 4] and electrons [2, 5] were detected in such heterosphase systems by the methods of optical spectroscopy. In the present letter we report the observation of a quantum size effect, theoretically predicted by A.L. Éfros and Al.L. Éfros [6], in the energy spectrum of holes in a potential well which results from the electron charge density distribution in the microscopic crystal.

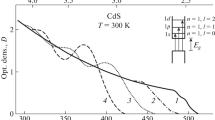
Figure 1 shows a spectrum of the interband absorption of microscopic CdS crystals with a mean radius $\bar {a}$ ≈ 20 Å, which was measured at T = 4.2 K, and the spectra of the second derivative ∂²А/∂λ², which were measured at T = 4.2, 77, and 300 K. The average size of the microscopic crystals was measured by the method of small-angle scattering of X-rays [1]. The large-scale oscillations observed in the spectra are caused, as was shown elsewhere [5], by the transitions to the electron size quantization levels in the conduction band. Figure 1 also shows that a structure, clearly seen in the spectra of the second derivative at T = 4.2 and 77 K, manifests itself at low temperatures in the spectral region of the transitions to the first level of electron size quantization. As the temperature is raised, this structure becomes diffuse, and at room temperature if cannot be resolved at all even in the spectra of the second derivative. A similar situation occurs in the range of values of the microscopic-crystal radii 15 Å ≤ $\bar {a}$ ≤ 23 Å, which are smaller than the exciton radius (r_exc = 30 Å) in CdS crystals. The magnitude of the splitting, which depends on the size of the microscopic crystals, increases with decreasing $\bar {a}$.

Fig. 1.

Spectrum of interband absorption of microscopic CdS crystals (a = 20 Å) at T = 4.2 К and spectra of the second derivative ∂²А/∂λ² at T = (1) 4.2, (2) 77, and (3) 300 K.

As was shown theoretically in [6], this effect can be attributed to the Coulomb interaction of an electron-hole pair produced as a result of absorption of a light quantum. In the range of microscopic-crystal sizes a < r_exc, the energy of motion of an electron in a quantum well is in fact considerably higher than the energy of the Coulomb interaction of the quantum well with the hole. In the case of semiconducting materials with m_e $\ll$ m_h (m_e, and m_h are the effective masses of the electron and the hole), the Coulomb potential of the electron which affects the hole may therefore be assumed averaged over the fast motion of the electron (adiabatic approximation). If the electron is situated at the lower size-quantization level, this potential will have a minimum at the center of the semiconducting sphere and near the bottom we can write the potential in the form [6]:

$$V({{r}_{h}}) = - \alpha \frac{{{{e}^{2}}}}{{\kappa a}} + \frac{{{{\pi }^{2}}}}{3}\frac{{{{e}^{2}}}}{{\kappa a}}\frac{{r_{h}^{2}}}{{{{a}^{2}}}};\quad {{r}_{h}} \ll {{a}_{h}},$$

(1)

where κ is the dielectric constant of the crystal, the numerical factor α = 2$\int_0^\pi d$ysin²y/y ≈ 2.4 takes into account the electron charge density distribution at this level, and $r_{h}^{0}$ is the distance by which the hole is displaced from the center of the sphere. As we can see in Fig. 1, allowance for the Coulomb interaction in the microscopic crystals with a radius smaller than the exciton radius (a < r_exc) leads to the appearance in the hole of an additional potential well of depth on the order of е²/κа.

The role played by the additional potential well in the formation of the energy spectrum of the holes is determined essentially by the ratio of the well depth and the energy of the size quantization of the holes in the microscopic crystal. The relative contribution of these quantities, which depends on the size of the microscopic crystals, can be estimated in order of magnitude. It can easily be shown that the energy of the Coulomb interaction ~е²/κа is higher than the energy of the size quantization of the holes, ~${{\hbar }^{2}}$/m_ha², if the microscopic-crystal radii satisfy the condition

$$a > \frac{{\kappa {{\hbar }^{2}}}}{{{{m}_{h}}{{e}^{2}}}} \equiv {{a}_{h}},$$

where a_h is the Bohr radius of the hole. For most of the semiconducting materials a_h $\lesssim$ 10 Å and this condition is satisfied down to the smallest realistically attainable sizes of the microscopic crystals. In semiconducting materials with m_c $\ll$ m_h, the energy spectrum of the holes is thus determined by the electron-motion-averaged potential of the Coulomb interaction, rather than by the size quantization of the holes in the potential well of the microscopic crystal, as was assumed in [7].

Since the condition m_e $\ll$ m_h is satisfied for CdS crystals, and since the Bohr radius is no greater than a_h $\lesssim$ 7 Å, the energy spectrum of the holes for the sizes under study must be determined by the potential of the Coulomb interaction of the hole with the electron. As we can see from (1), this potential has the form of the potential of a three-dimensional harmonic oscillator. The motion of a hole in such a potential leads to the appearance in its energy spectrum of an equally spaced series of lines whose spacing is determined by [6]

$$\Delta \hbar {{\omega }_{h}} = {{\left( {\frac{8}{3}\frac{{{{e}^{2}}}}{{\kappa a}}\frac{{{{\hbar }^{2}}{{\pi }^{2}}}}{{{{m}_{h}}{{a}_{2}}}}} \right)}^{{1/2}}}.$$

(2)

The wave functions of the holes which correspond to these states differ markedly from the wave functions which describe their motion in the absence of Coulomb interaction. As a result, the selection rules change and the optical transitions from each level to a lower size-quantization level become resolved [6]. This circumstance accounts for the appearance of a structure in the spectrum of the interband transitions to the first level on the size quantization of the electron (see the inset in Fig. 1).

Figure 2 is a plot of the experimental curve for the splitting, Δ$\hbar$ω, versus the mean radius of the microscopic crystals $\bar {a}$. We see that the splitting is proportional to ${{\bar {a}}^{{ - 3/2}}}$, consistent with (2). The phenomenon which we have observed can thus be qualitatively described in terms of a very simple model which takes into account the interaction of an electron with the hole in a simple parabolic zone. A quantitative analysis of the experimental results cannot, however, be carried out without the use of a theory which takes the actual structure of the valence band of CdS into account.

Fig. 2.

Experimental dependence of the splitting on the size of the microscopic crystals.

Our results thus show that for a size of the microscopic crystals in the range r_exc < a < a_h the Coulomb interaction leads to the appearance of an additional potential well which determines the energy spectrum of the holes in the microscopic crystal. A similar phenomenon should also occur in quasi-two-dimensional structures with quantum wells.