Generation of Reflected Second Harmonic at Semiconductor Quantum Dots

Generation of the reflected second harmonic has been observed for the first time in a composite material: a glass matrix containing microscopic CdSe crystals, ranging in size from 500 to 50 Å. The violation of polarization selection rules in the second-harmonic generation indicates that the nonlinear sources are of a fluctuational nature. A size effect has also been observed: The intensity of the second harmonic increases by a factor of 102 as the size of the microscopic crystals is reduced. A possible mechanism for this size effect is analyzed.

Generation of the reflected second harmonic has recently attracted particular interest as a method for studying the properties of various 2D and quasi-2D structures. This method has been used to study the surface structure of semiconductors [1] and metals [2], a phase transition on a silicon surface [3], the properties of Langmuir-Blodgett molecular films [4], insulator-metal phase transitions in diamond-like films [5] and films of synthetic metals [6], and a structural phase transition in ferroelectric films [7].

Second-harmonic generation in quasi-zero-dimensional structures has been studied previously only for metals. Specifically, size effects in a giant second-harmonic amplification in ultrasmall silver particles, with an average size ~10–100 Å, were studied in [8]. The literature reveals [9] several discussions of the need to study nonlinear-optics effects in composite ultradisperse semiconducting materials consisting of glass matrices with microscopic semiconductor crystals. We should stress that this discussion has been conducted in terms of cubic nonlinear-optics effects. It has been assumed that quadratic effects, such as second-harmonic generation, would not occur in a composite medium of this sort, since such a medium is centrally symmetric at the macroscopic level. However, studies of rough surfaces [10] and of nonuniform thin films [7] have shown that a diffuse and depolarized reflected second harmonic is in fact generated in media which are centrally symmetric at the macroscopic level and which have a random inhomogeneity. The generation results from fluctuations in a nonlinear susceptibility.

In the present experiments the second harmonic was generated upon the reflection of the beam from a Nd:YAG laser (with a wavelength of 1064 nm, a pulse length of 15 ns, and a pulsed power density ~1 MW/cm²) from the surface of a composite material consisting of microscopic CdSe crystals in a glass matrix [11]. The cadmium selenide concentration was $\lesssim {\kern 1pt} 0.5$% by mass and uniform over the entire volume of the sample. The average size of the microscopic crystals varied from 500 to 50 Å in the various parts of the sample.

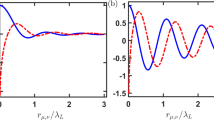
Figure 1 shows the intensity of the p-polarized second harmonic, I_2ω, found upon reflection of p-polarized pump light from parts of a sample differing in the average size of the microscopic crystals, $\bar {R}$. The intensity I_2ω increases by two orders of magnitude as $\bar {R}$ is reduced from 500 to 50 Å.

Fig. 1.

Intensity of the second harmonic, I_2ω, versus the average size of the microscopic CdSe crystals, $\bar {R}$. The monotonic variation of $\bar {R}$ along the sample was monitored at a qualitative level on the basis of the spectral shift of the optical absorption edge. The inset is a schematic diagram of the electron energy levels in the microscopic crystals in an interval Δ = 2$\hbar$ω – E_g ($\hbar$ω = 1.17 eV, E_g = 1.75 eV) near the top of the valence band (${v}$) and near the bottom of the conduction band (c). The corresponding band boundaries are shown by dashed lines. The dashed arrow in part b of the inset shows a resonant pair of levels. Numerical estimates were calculated for the averaged level spacing ${{\delta }_{{c,{v}}}}$ ~ Δ/${{N}_{{c,{v}}}}$, where ${{N}_{{c,{v}}}}$ are the numbers of electron states with energies in the interval Δ.

To determine the nature of the nonlinear sources in the composite material, we studied the violation of the s, s selection rule [10] in the generation of the reflected second harmonic. In the second-harmonic signal detected in the case of an s-polarized pump, the intensity of the s component (which is forbidden by the polarization selection rules for a homogeneous medium with a smooth boundary) turned out to be comparable to the intensity of the (allowed) p, p harmonic. In other words, the depolarization of the second harmonic resulted in a pronounced disruption of the s, s selection rule. To pursue this matter, we studied the directional pattern of the second harmonic. The second harmonic generated upon reflection from the smooth boundary of a homogeneous medium (homogeneous down to the microscopic scale) is specular, while the emission of the reflected second harmonic generated by a randomly inhomogeneous medium should have a substantial diffuse component of fluctuational origin. For these particular test samples the reflected second harmonic was indeed of this diffuse type. The emission of the second harmonic was distributed essentially uniformly over a solid angle of 2π sr.

It is logical to assume that the diffuse nature and the depolarization of the second harmonic result from a random orientation of the microscopic crystals, which leads to the value 〈α₂〉 = 0, where α₂ is the quadratic polarizability of an individual microscopic crystal, and the angle brackets mean a statistical average over the ensemble of realizations. The intensity of the p-polarized specular component of the second harmonic then satisfies $I_{{2\omega }}^{{{\text{spec}}}}$ ~ |〈α₂〉|² = 0 (ω is the pump frequency). In other words, the emission of the second harmonic is of a purely fluctuational nature. The intensity of the diffuse, depolarized component of the second harmonic is then given by

$${{I}_{{2\omega }}}{\text{/}}I_{\omega }^{2}\sim {{n}^{2}}{{l}^{3}}\langle {\text{|}}L(2\omega ){{\alpha }_{2}}(\omega ){{{\text{|}}}^{2}}\rangle ,$$

(1)

where I_ω is the pump intensity, n is the volume concentration of the microscopic crystals, L is a local-field factor (which reflects that linear response of the system at the frequency of the second harmonic which is induced by the nonlinear polarization of the microscopic crystals), and l is a correlation length characteristic of the length scale of the fluctuations in L and α₂. In deriving (1) we ignored retardation effects (assuming l ~ n^–1/3 $\ll$ c/(ω). We also ignored regular variations in the concentration and the average size of the microscopic crystals over the region illuminated by the pump light (we assumed that the system was statistically homogeneous and isotropic). We furthermore made use of the circumstance that for this particular system we can ignore both the absorption at the pump frequency (because of the relation $\hbar$ω < E_g, where $\hbar$ω = 1.17 eV is the energy of the pump photon, and E_g = 1.75 eV is the band gap of CdSe) and the absorption at the frequency of the second harmonic (because of the relation l < [κ(2ω)]^–1, where κ is the effective absorption coefficient of the medium: κ(ω) ~ ω/c[4πnIm〈α₁(ω)〉]^1/2, where α₁ is the linear polarizability of the microscopic crystals).

In general, each quantity on the right side of (1) depends on the size of the microscopic crystals. For L and α₂ this dependence results primarily from the size quantization of the energy of the electron states in the valence and conduction bands in the microscopic crystals. Numerical estimates of the average distance between adjacent energy levels for R ~ 500 Å and R ~ 50 Å (R is the radius of the microscopic crystals) are shown in insets (a, b) of Fig. 1. At R ~ 500 Å, we cannot ignore the size quantization, so we find the following estimate in the frequency range of interest here (ω < E_g/$\hbar$ < 2ω):

$$\langle {\text{|}}L(2\omega ){{\alpha }_{3}}(\omega ){{{\text{|}}}^{2}}\rangle \sim {{[{{\Omega }_{0}}{{\bar {R}}^{3}}{\text{/}}(\omega {{\varepsilon }_{0}})]}^{2}}.$$

(2)

Here ε₀ = m²e⁵${{\hbar }^{{ - 4}}}$ ~ 2 × 10⁷ G and ω₀ = me⁴${{\hbar }^{{ - 3}}}$ ~ 4 × × 10¹⁶ s^–1 are atomic scale values of the electric field and the frequency, and $\bar {R}$ = 〈R〉. At R ~ 50 Å, we can restrict the discussion to another limiting case: the resonant two-level approximation. We assume that the response of the system is dominated by interband transitions between only one pair of levels, which are exactly at resonance with the electromagnetic field at the frequency of the second harmonic, 2ω (see inset b in Fig. 1). In addition to the homogeneous line broadening in the conduction band, which is characterized by the spectral width γ, we need to allow for the inhomogeneous broadening, which stems from the statistical scatter in the size of the microscopic crystals. We then find the estimate

$$\langle {\text{|}}L(2\omega ){{\alpha }_{2}}(\omega ){{{\text{|}}}^{2}}\rangle \sim {{[\Omega _{0}^{2}{{\bar {R}}^{3}}f({{\rho }_{{{\text{res}}}}}){\text{/}}(\omega \gamma {{\varepsilon }_{0}})]}^{2}},$$

(3)

where f(ρ) is the distribution function of the random quantity ρ = R/$\bar {R}$, and ρ_res = R_res/$\bar {R}$, where R_res is the value of $\bar {R}$ which corresponds exactly to the resonance. In deriving (3) we assume R_res ~ $\bar {R}$, and we assumed that the function f varies slowly: f   '(ρ_res)$\hbar$γ/$\epsilon$ $\lesssim$ 1, where $\epsilon$ = π²${{\hbar }^{2}}$/(2m_c${{\bar {R}}^{2}}$) is the scale of the size quantization of the energy in the conduction band, and m_c is the effective mass of an electron in the conduction band.

For the system of interest here we have n${{\bar {R}}^{3}}$ = const ~ 10^–2 and l ~ n^–1/3. Using these relations, we find the following estimate for the ratio of the second-harmonic intensities in the cases $\bar {R}$ = 50 Å and $\bar {R}$ = 500 Å from (l)–(3):

$$\begin{gathered} K \equiv {{I}_{{2\omega }}}(\bar {R} = 50\,{\text{\AA}}){\text{/}}{{I}_{{2\omega }}}(\bar {R} = 500\,{\text{\AA}}) \\ \sim {{10}^{{ - 3}}}{{[{{\Omega }_{0}}{{\gamma }^{{ - 1}}}f({{\rho }_{{{\text{res}}}}}){{{\text{|}}}_{{\bar {R} = 50\,{\text{\AA}}}}}]}^{2}}. \\ \end{gathered} $$

(4)

Using the experimental value K ~ 10², we find Ω₀γ^–1f ~ 3 × 10² from (4). With $\hbar$γ ~ 10^–2 eV we then find f ~ 10^–1. In other words, the fraction of the resonant microscopic crystals determined by the value f(ρ_res)$\hbar$γ/$\epsilon$ should be ~1%. These estimates show that a resonance at the second-harmonic frequency in the optical response of the microscopic crystal with $\bar {R}$ ~ 50 Å can completely explain the intensification of the second-harmonic generation observed experimentally with decreasing $\bar {R}$.

In summary, we have observed for the first time a generation of the reflected second harmonic in a composite material: a glass containing microscopic crystal of CdSe. We believe that the diffuse nature and the depolarization of the second harmonic observed in these experiments can be explained by the random orientation of the microscopic crystals. This random orientation leads to fluctuations in the nonlinear susceptibility of the system. The strong size dependence of the intensity of the second harmonic stems from resonant effects in the optical response of the microscopic crystals, because of a size quantization of the electron spectrum.