Charge-orbital Ordering, Magnetic State, and Exchange Couplings in Quasi-One-Dimensional Vanadate V₆O₁₃

Charge and orbital ordering, magnetic state, and exchange couplings in quasi-one-dimensional vanadate V₆O₁₃, a potential cathode material for Li-ion batteries, are investigated using the density functional theory with Coulomb interaction correction method (DFT + U). While the difference between ${{t}_{{2g}}}$ orbital occupancies of V⁴⁺ (with a nominal $3{{d}^{1}}$ electronic configuration) and V⁵⁺ ions is large and gives direct evidence for charge and orbital ordering, the screening is so effective that the total $3d$ charge disproportionation is rather small. Our results show that the occupied ${{t}_{{2g}}}$ states of V⁴⁺ ions in the single V–V layer form a spin-singlet molecular orbital, while the rest half of V⁴⁺ ions in the structurally distinct double V–V layers order antiferromagnetically in the low-temperature insulating phase of V₆O₁₃. We conclude that the metal-insulator transition and low-temperature magnetic properties of V₆O₁₃ involve the spin-Peierls transition assisted by orbital ordering and concomitant distortions of the crystal structure.

INTRODUCTION

During the last several decades transition metal compounds have attracted much attention because of their intriguing low-temperature electronic and magnetic properties [1–4]. Many of them display complex types of spin, charge, and orbital orderings which are often accompanied by metal-insulator phase transitions driven by strong electron correlation effects [1–29]. A fascinating example is ferrimagnetic magnetite Fe₃O₄, in which charge-orbital ordering (COO) sets in below the Verwey metal-insulator transition at ~120 K [30, 31]. The details of the low-temperature charge-orbital ordering and electronic properties of Fe₃O₄ have been at the focus of hot recent debates [32–51].

The specific orbital ordering (OO) often results in the formation of a nonmagnetic spin-singlet state. In particular, the so-called orbital-assisted (spin) Peierls state has recently been proposed to occur below the metal–insulator transition in CuIr₂S₄ and MgTi₂O₄, resulting in the octamer COO and chiral OO, respectively [52–56]. Another example is the recently synthesized La₂RuO₅, in which the competition between the Peierls-like and Jahn–Teller effects leads to a remarkable insulator-to-insulator phase transition below ~160 K accompanied by the formation of a nonmagnetic spin-singlet ground state [57–59]. These examples show either magnetic or nonmagnetic (spin-singlet) behaviors. On the other hand, the coexistence of long-range magnetic and nonmagnetic spin-singlet states seems to be a rather rare phenomenon which has (only) been proposed to occur in the low-temperature monoclinic phase of V₆O₁₃, a potential cathode material for Li-ion batteries [60, 61]. The low-temperature electronic structure, magnetic properties, and microscopic parameters of the charge-orbital ordering of V ions in V₆O₁₃ still remain to be controversial [62–65].

Vanadium oxide V₆O₁₃ is a member of a homologous Wadsley series V_mO_{2m + 1} with $m > 1$. It is a promising compound in view of the possible applications in Li-ion batteries as a cathode material because of its very high capacity of ~310 mA h/g [60, 61]. It is a mixed-valent oxide containing both 4+ and 5+ V ions (in the nominal $3{{d}^{1}}$ and $3{{d}^{0}}$ electronic state, respectively) with a corresponding ratio 2-to-1. At room temperature, V₆O₁₃ is a paramagnetic metal which has a 2D layered crystal structure with monoclinic $C2{\text{/}}m$ space group and three crystallographically inequivalent vanadium sites [66]. The lattice consists of edge- and corner-sharing strongly distorted VO₆ octahedra, which form two types of alternating vanadium layers—single and double V–V layers, respectively (with the single V–V layer consisting of the chains of V1 atom, whereas the double layer contains the chains of the alternating V2 and V3 ions)—in the ab plane with corner sharing between the layers. This quasi-one-dimensional behavior reflects in the electrical resistivity measurements which reveal a remarkable anisotropy of the transport properties of V₆O₁₃ with the lowest resistivity along the b axis [67]. It was also confirmed by the optical reflectivity (conductivity) [68–70] and angle-resolved photoemission measurements (ARPES) [71–73].

Upon further cooling, V₆O₁₃ undergoes a first-order metal–insulator transition at ~150 K below which conductivity abruptly drops by four orders of magnitude [67]. The phase transition is accompanied by a crystal structure distortion to the monoclinic $Pc$ phase and by a remarkable decrease in magnetic susceptibility [74, 75]. The low-temperature crystal structure of V₆O₁₃ was recently refined using single crystal X-ray diffraction data [76]. Thus, the monoclinic $Pc$ crystal structure with four formula units per unit cell was proposed, in which all vanadium atoms move out of the mirror plane and no center of symmetry is found. A bond valence sum analysis across the phase transition at 150 K suggests a charge transfer between the V1 and V3 ions. In addition, by means of nuclear magnetic resonance the phase transition at 150 K was interpreted as charge ordering at which the half of V⁴⁺ ions form spin-singlet pairs [74, 75]. The remaining V⁴⁺ ions are paramagnetic and order antiferromagnetically upon cooling below ~55 K. In this respect, V₆O₁₃ is a remarkable mixed-valent system with a charge-orbital ordering transition to occur at 150 K [77], in which a nonmagnetic spin-singlet state at the half of V⁴⁺ ions coexists with a long-range antiferromagnetic ordering of the remaining V⁴⁺ ions (below the Néel temperature ~55 K) [74, 75].

The electronic properties of V₆O₁₃ across the metal–insulator transition were investigated by means of ARPES [71–73]. In particular, in the metallic phase two well defined electronic branches were observed: a quasi-one-dimensional band located at –0.8 eV below the Fermi level, which has dispersion only along the b axis, and a weak almost flat along the a axis feature at –0.2 eV which has an upward parabolic-like dispersion toward the Fermi level. The energy bands near the Fermi level were ascribed to the zigzag chains of mixed 4+ and 5+ V ions [72, 73]. Below the transition both bands shift to the lower energies resulting in an opening of the energy gap of about 0.2 eV. In addition, dispersion of the energy band at –0.8 eV becomes smaller in the insulating phase, whereas the band right below the Fermi level shifts to about –0.4 eV.

RESULTS AND DISCUSSION

Electronic Structure

In order to resolve the details of the electronic structure, charge-orbital ordering, and magnetic properties of the low-temperature (LT) phase of V₆O₁₃ we perform the DFT and DFT + U band-structure calculations within the linear muffin-tin orbital atomic-sphere approximation tight-binding (TB-‑LMTO) approach (Stuttgart TB-LMTO code) [78–80]. In these band-structure calculations we use the experimental crystal structure parameters of the LT phase of V₆O₁₃ [66, 67]. In agreement with previous studies [81], our LDA calculations (with the Hubbard $U = 0$ eV and Hund’s $J = 0$ eV) give a metal (in a sharp contrast to experiment [67, 72, 73]) with a partially filled V $3d$ band predominantly originated from the V ${{t}_{{2g}}}$ states (not shown here). The V ${{t}_{{2g}}}$ states are located in the vicinity of the Fermi level between –1 and 2 eV, whereas the V ${{e}_{g}}$ states are shifted to the higher energy range between 2 and 5 eV due to a large octahedral crystal-field splitting. Note, however, that a significant distortion of the VO₆ octahedra in LT V₆O₁₃ lifts the V $3d$ ${{t}_{{2g}}}$ orbital degeneracy resulting in a significant crystal-field splitting of the ${{t}_{{2g}}}$ states in the range of 0.2–0.6 eV. Thus, the V1a/V1b ${{d}_{{zx}}}$/${{d}_{{xy}}}$ and V3 ${{d}_{{yz}}}$ spin-orbitals are most occupied (with occupation of about 0.4 electrons) and located at about 0.4 eV, whereas the remaining V $3d$ states are shifted by 0.4–0.6 eV above. The crystal field splitting of the V2 ${{t}_{{2g}}}$ states is considerably smaller comparing to the V1 and V3 ions (0.2 eV). In addition, the lowest in energy the ${{d}_{{yz}}}$ V2a, 2b orbitals are located at about 0.7 eV. The O $2p$ states are fully occupied and appear between –7 and –2 eV below the Fermi level. The crystal field splitting gives rise to appreciable degree of $3d$ orbital polarization of the V1 and V3 ions (resulting in a 0.2–0.3 difference of the ${{t}_{{2g}}}$ orbital occupancies), whereas the V2 ${{t}_{{2g}}}$ occupancies are nearly the same.

Next, we take into account the strong electron correlations in the V $3d$ shell using the static mean-field DFT + U approach [79, 80]. In Fig. 1 we show the partial V $3d$ density of states (DOS) obtained from the LDA + U calculations using the Coulomb interaction parameter $U = 3.75$ eV and Hund’s exchange coupling $J = 0.9$ eV, which are typical for the V ion. We note that further increase in the Hubbard U value does not qualitatively change the ground state and basically only leads to increasing of the energy gap value. In our DFT + U calculations we consider different magnetic patterns (using a lower symmetry), e.g., realized in the $a \times 2b \times c$ supercell of LT V₆O₁₃ [74, 75]. Interestingly, for different magnetic structures our DFT + $U$ calculations yield the same charge-orbital ordering pattern with a total energy difference being varied in the order of 0.1 eV/cell. We obtain that the V ions in double layers formed by the V2a/V3a and V2b/V3b ions are aligned ferromagnetically with magnetic moments of $- 0.14{\text{/}} - 0.84{\kern 1pt} {{\mu }_{{\text{B}}}}$ and 0.11/0.86 ${{\mu }_{{\text{B}}}}$, respectively, while the layers are stacked antiferromagnetically along the a axis. Moreover, the V1a and V1b sites are antiferromagnetic with spin moments of 0.86μ_B and $- 0.85{\kern 1pt} {{\mu }_{{\text{B}}}}$, respectively. In the following all results are presented for this magnetic structure.

Fig. 1.

(Color online) Partial DOS obtained from the LDA + U calculations with $U = 3.75{\kern 1pt}$eV and $J = 0.9{\kern 1pt}$ eV for the low-temperature $Pc$ phase of V₆O₁₃. The top of the valence band is shown by dotted lines.

In agreement with photoemission data [72, 73], the DFT + U calculations result in an opening of the energy gap of 0.2 eV. The occupied V $3d$ states are strongly localized and form two well defined bands below the Fermi level and in the energy range between –2 and –0.6 eV. These findings qualitatively well agree with the ARPES data [72, 73] and give us opportunity to discriminate basic features of the experimental spectra. Thus, the occupied V3a bands are strongly localized and form a weakly dispersive band right below the Fermi level in the energy range of –0.5–0 eV. On the other hand, the occupied V1a/V1b $3d$ bands are shifted to the lower energies and located between –2 and –0.5 eV. The occupied majority V1a band is strongly localized and dispersionless, whereas the occupied minority spin V1b band has considerable dispersion along the b axis and has a bandwidth of about 1.5 eV. Fully occupied $2p$ oxygen states form a wide band between –7 and –2 eV which manifests itself in Fig. 1 because of appreciable hybridization between the V $3d$ and O $2p$ states. It is remarkable that a degree of the V $3d$–O $2p$ hybridization is larger for the V2a/V2b ions.

Charge-Orbital Ordering and Magnetic State

We note that the self-consistent solution obtained by DFT + U is charge and orbitally ordered. The integrated charge state of the V $3d$ bands in the energy range between –2 eV and the Fermi level indicates formation of the ${{t}_{{2g}}}$ charge and orbital ordered state in which one of the V1 and V3 ions each has one ${{t}_{{2g}}}$ orbital occupied, whereas all the V2 ${{t}_{{2g}}}$ orbitals are empty (see $\int {{{\text{N}}}_{d}}(\varepsilon )d\varepsilon$ in Table 1). According to this we label the V1 and V3 as 4+ ($3{{d}^{1}}$), and V2 as 5+ ($3{{d}^{0}}$) V ions. This exactly supports previous proposal that the bands near E_F are derived from the zigzag chains with mixed 4+ and 5+ V sites [72, 73]. Moreover, our analysis of the V $3d$ occupation matrices suggests the ${{d}_{{xz \uparrow }}}$/${{d}_{{xy \downarrow }}}$ character for the occupied V1a/V1b ions which are almost completely filled with the occupation number of ~0.8. The occupied V3a/V3b states are predominantly of the ${{d}_{{yz}}}$ character with population of 0.8$\bar {e}$. On the other hand, the remaining two ${{t}_{{2g}}}$ orbitals of the V1 and V3 ions have a significantly smaller population of about 0.2 which gives an orbital order parameter of 60% of the ideal value. In contrast, the V2a/V2b $3d$ orbitals do not reveal any orbital polarization. Moreover, the V2a/V2b ${{t}_{{2g}}}$ orbital occupancies do not exceed 0.27 resulting in a remarkable charge disproportionation within the ${{t}_{{2g}}}$ subshell between the V1/V3 and V2 ions. Interestingly that due to considerably larger hybridization between the O $2p$ and V2a/V2b $3d$ states the corresponding $3d$ charge disproportionation inside the atomic spheres of the V1/V3 and V2 ions is rather small, consistent with previous estimates for charge-ordered transition metal oxides [12–14, 28, 29, 34, 35, 40–43, 46, 47]. The corresponding orbital orientations are depicted in Fig. 2.

Table 1. Integrated V $3d$ density of states in the range from –2 to 0 eV ($\int {{{\text{N}}}_{d}}(\varepsilon )d\varepsilon$), the corresponding sums of the ${{t}_{{2g}}}$ and ${{e}_{g}}$ occupancies (${{\Sigma }_{{{{t}_{{2g}}}}}}$ and ${{\Sigma }_{{{{e}_{g}}}}}$, respectively), magnetic moments (M), and occupations of the most populated ${{t}_{{2g}}}$ orbitals (n) calculated by DFT + U for inequivalent V atoms in the low-temperature $Pc$ phase of V₆O₁₃

Fig. 2.

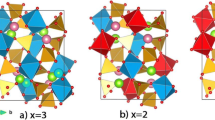
(Color online) Crystal structure and orbital order projected on the (100) plane as obtained by LDA + U with $U = 3.75$ eV and $J = 0.9$ eV for the LT phase of V₆O₁₃. Footnote

The angular distribution of the V $3d$ electron density is calculated as $\rho (\theta ,\phi ) = \sum\nolimits_{m,m'} {{n}_{{m,m'}}} Y_{m}^{ * }(\theta ,\phi ) {{Y}_{{m'}}}(\theta ,\phi )$, where ${{n}_{{m,m'}}}$ is the occupation matrix of $3d$ states of the corresponding V ions. The occupation matrices were calculated by the LDA + U with $U = 3.75{\kern 1pt}$ eV, $J = 0.9{\kern 1pt}$eV for the LT $Pc$ phase of V₆O₁₃. ${{Y}_{m}}(\theta ,\phi )$ are the corresponding spherical harmonics.

Three types of ab planes are shown: two double layers (with $x = \pm \frac{a}{4}$) which include zigzag chains running along the b axis containing both 4+ and 5+ V ions, and a single layer ($x = 0$) which is formed by V⁴⁺ ions. The size of orbital corresponds to its occupancy. Red and blue colors correspond to the majority and minority spin, respectively.

Exchange Couplings and Spin-Singlet Pair Formation

In Table 2 we show the exchange couplings as calculated using the Green’s function method within the DFT + U approach [79, 80]. In particular, the electronic structure calculations result in a relatively weak interlayer coupling (less than 85 K between the V1–V2 sites). In the double V–V layer ($x = \pm a{\text{/}}4$) the exchange couplings in the zigzag chain (along the b axis) are rather weak and ferromagnetic (see ${{\Delta }_{{{\text{bv}}}}}$ or ${{\Delta }_{{{\text{bb}}}}}$ V2a–V3a and V2b–V3b in Table 2), whereas the inter-chain exchanges are remarkably large and dominant (${{c}_{{||}}}$ for V2a–V3a and V2b–V3b). In contrast, the inter-chain couplings in the single layer ($x = 0$) (see ${{c}_{{||}}}$) are antiferromagnetic and considerably smaller than the intra-chain exchanges (${{\Delta }_{{{\text{bv}}}}}$ V1a–V1b or ${{\Delta }_{{{\text{bb}}}}}$ V1b–V1b). Therefore, in the single layer the V 4+ ions form a sawtooth-like spin-1/2 zigzag chains along the b axis which are (relatively) weakly coupled to each other. The base–base exchange coupling in the Δ‑chain between the ${{d}_{{xy}}}$ orbitals (ferro-orbitally ordered) on the neighboring V1b sites is large and antiferromagnetic (see ${{\Delta }_{{{\text{bb}}}}}$ V1b–V1b). Its amplitude is considerably larger than the mean base–vertex coupling (${{\Delta }_{{{\text{bv}}}}}$ V1a–V1b). The corresponding ratio between the base–base and mean base–vertex couplings in the V1 $\Delta$-chain (${{J}_{{{\text{bb}}}}}$/${{J}_{{{\text{bv}}}}}$) is smaller than the upper critical value of 1.53 for the ${{J}_{{{\text{bb}}}}}$/${{J}_{{{\text{bv}}}}}$ ratio (with equal base–vertex couplings), below which the spin gap state occurs in the sawtooth lattice (down to the low critical value of about 0.49) [82, 83]. Based on this we conclude that a spin gap is opened in the single V–V layer of the system (i.e., the spin-singlet V–V state forms) with the gap minimum at $k = \pi$ due to an orbital-assisted (spin) Peierls mechanism. In addition, the effect of a larger antiferromagnetic coupling in the base–vertex bonds between the nearest V1a–V1b sites in the unit cell (${{J}_{{{{\Delta }_{{{\text{bv}}}}}}}} = - 365$ K, while another is of ‒194 K) probably stabilizes a dimer singlet ordering corresponding to that direction. Our analysis disproves the previously proposed formation of the one-dimensional Heisenberg chain in the single layer accompanied by a spin-singlet ground state in the double layer of V₆O₁₃. In contrast, we propose a spin-singlet ground state in the single layer which also naturally agrees with analysis of the crystal structure below the phase transition at 150 K. In fact, analysis of the refined low-temperature crystal structure of V₆O₁₃ below 150 K suggests the formation of alternating “small” (2.98 Å) and “large” V1–V1 distances (3.16 Å) in the zigzag V‒V chains of the single layer. At the same time, above 150 K these distances are the same, of 3.05 Å. Moreover, the interatomic V–V distances in the zigzag chains in the double layer are not affected by the phase transition and remain almost the same above and below 150 K, about 3.01 Å.

Table 2. Exchange couplings between different V ions are shown. The values are given in kelvin. ${{\Delta }_{{{\text{bb}}}}}$ and ${{\Delta }_{{{\text{bv}}}}}$ denote the base–base and mean base–vertex exchange couplings in the zigzag chains along the b axis. Exchange couplings between zigzag chains (couplings along the c axis) are shown by ${{c}_{{||}}}$

CONCLUSIONS

In conclusion, using the DFT and DFT + U methods we determined the charge-orbital ordering, magnetic state, and exchange couplings of the quasi-one-dimensional V₆O₁₃, a potential cathode material for Li-ion batteries. Our results reveal a remarkable coexistence of the nonmagnetic spin-singlet state at the half of V⁴⁺ ions with the formation of a long-range antiferromagnetic ordering of the remaining V⁴⁺ ions in the double V–V layers below the Néel temperature. Our analysis disproves the previously proposed formation of the one-dimensional Heisenberg chain in the single layer with a spin-singlet state in the double layer of V₆O₁₃. Our results are in agreement with analysis of the behavior of the crystal structure and magnetic properties of V₆O₁₃ at the metal–insulator phase transition.