Sound-like Oscillations in the Polar Phase of Superfluid ³He in a Nematic Aerogel

The acoustic spectrum of the polar phase of superfluid ³He in nematic aerogel has been studied. An equation determining the dispersion of sound oscillations of the system has been derived. Solutions of the system have been obtained for low-frequency oscillations, whose propagation velocity is much lower than the speed of first sound in pure ³He, for directions along and across the anisotropy axis of the aerogel. In the same approximation, a solution for purely shear oscillations of the system has been found under special boundary conditions corresponding to an incompressible liquid surrounding the system. The temperature dependence of the found frequencies has been compared with the existing experimental data.

1 INTRODUCTION

The polar phase of superfluid ³He belongs to topological superfluid phases and has a number of unique properties. The order parameter of this phase is a complex 3 × 3 matrix ${{e}^{{i\varphi }}}{{d}_{\mu }}{{m}_{j}}$, where d_μ and m_j are the components of the unit vectors in the spin and orbital spaces, respectively [1]. The spectrum of quasiparticles in the polar phase has a topologically stable Dirac line of zeros on the equator of the Fermi surface in the plane perpendicular to the vector m. As a result, superfluid properties of the system are described by a uniaxial superfluid density tensor with the maximum principal value along the m direction. The topological properties of this phase are also manifested in the existence of a specific excitation branch at the phase interface, which is due to the principle of correspondence and belongs to Majorana surface states [2]. The polar phase can be observed experimentally only in the presence of nematic aerogel with a high degree of anisotropy, i.e., aerogel where strands are well codirected (nafen, mullite aerogel) [3, 4]. In the presence of strands of the aerogel in the system, interesting topological defects—half-quantum vortices [5, 6], which were observed in the experiment reported in [7]—can be stabilized. In addition to the mentioned topological properties of the polar phase, the superfluid response of the system is also of interest. Superfluid properties of the system can be observed in experiments on oscillating of the aerogel inside the volume filled with superfluid ³He [8, 9]. A feature of the problem is the effective interaction between the superfluid component and the framework of the aerogel. As a result, the oscillating spectrum of the system is determined not only by the superfluid properties of the polar phase but also by the elastic properties of the aerogel. Since the elastic properties of the nematic aerogel are obviously anisotropic, interesting mixed vibrational modes, which are impossible in the isotropic case, can be expected in the system. Two oscillating modes were detected in the mentioned experiments on oscillations of the nematic aerogel in superfluid ³He [8, 9]. One of the modes corresponds to mechanical vibrations of the system and is observed in the entire temperature range. The temperature dependence the frequency of the first mode is due both to the temperature dependence of the viscosity of ³He surrounding the aerogel and to change in the flow-lines around the aerogel at the time of the superfluid transition in the aerogel. An attempt to describe the temperature dependence of the frequency of the first mode taking into account the potential flow of superfluid currents through the aerogel under the condition that both the liquid and aerogel are incompressible was performed earlier [10]. The second oscillating mode appears only at the time of the superfluid transition in the aerogel. The features of the observed temperature dependence of the frequency for the second mode is its fast increase near the transition point with the subsequent approximate saturation at about 1.6 kHz. Such a low frequency of oscillations excludes the possibility of locking of the first sound of ³He in this mode. The frequency is saturated in a quite narrow temperature range of several hundredths of the transition temperature T_c. This feature distinguishes the observed mode from the “slow” mode excited in experiments on the propagation of sound in silica aerogels [11]. The aims of this work are to study the acoustic spectrum of the polar phase and nematic aerogel and to identify the experimentally observed second vibrational mode. The accurate derivation of the system of hydrodynamic equations necessary to solve this problem is a separate interesting item, but it is beyond the scope of this work. In this work, the acoustic spectrum of the system is determined using the system of linear hydrodynamic equations that can be obtained heuristically as in [12]. The system is solved for the actual case of low-frequency oscillations whose propagation velocity is much lower than the speed of first sound in pure superfluid ³He. Effective boundary conditions describing the case where the system is surrounded by an incompressible superfluid liquid are discussed qualitatively. It is noteworthy that the system of linear hydrodynamic equations for the polar phase in the nematic aerogel was derived in [13], but the results obtained in [13] cannot be used in this work because of inaccuracies in it.

2 LINEARIZED HYDRODYNAMIC EQUATIONS FOR THE POLAR PHASE IN THE NEMATIC AEROGEL

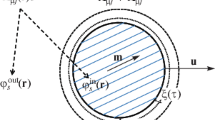
The system of hydrodynamic equations for the considered system consists of five equations describing the conservation laws of the mass of the aerogel, mass of ³He, the total momentum of the composite system, entropy (damping is ignored), and the potentiality of superfluid motion. The density of the aerogel ρ_a, the density of ³He ρ_l, entropy per unit volume s, superfluid velocity v_s, and local displacement vector of particles of the aerogel u are used as independent hydrodynamic variables. The last quantity can be used as an independent quantity under the no-slip condition between the aerogel framework and the normal component of ³He, which is satisfied at low frequencies of motion. In this case, the velocity of the normal component ${{({{v}_{{\text{n}}}})}_{i}} = {{\dot {u}}_{i}}$ and the total current density are determined by the expression j_i = (ρ_aδ_ij + (ρ_n)_ij)${{\dot {u}}_{j}}$ + (ρ_s)_ij(v_s)_j, where (ρ_s)_ij and (ρ_n)_ij (${{({{\rho }_{{\text{s}}}})}_{{ij}}} + {{({{\rho }_{{\text{n}}}})}_{{ij}}} = {{\rho }_{{\text{l}}}}{{\delta }_{{ij}}}$) are the tensors of the superfluid and normal components of ³He, respectively. The spin vector d and orbital vector m, which are hydrodynamic variables specific to the polar phase, are ignored. The former is not involved in motion because it is uncoupled with other hydrodynamic variables in the absence of the spin–orbit coupling. The inclusion of the latter exceeds the accuracy of the linear approximation and long-wavelength limit used below because the energy of the texture of the orbital vector includes higher derivatives of the displacement vector than the elastic energy of the aerogel. Thus, the linearized equations for the system under consideration have the form

$$\frac{{\partial \delta s}}{{\partial t}} + {{s}^{{(0)}}}{{\nabla }_{i}}{{\dot {u}}_{i}} = 0,$$

(1)

$$\frac{{\partial \delta {{\rho }_{{\text{a}}}}}}{{\partial t}} + \rho _{{\text{a}}}^{{(0)}}{{\nabla }_{i}}{{\dot {u}}_{i}} = 0,$$

(2)

$$\frac{{\partial \delta {{\rho }_{l}}}}{{\partial t}} + {{({{\rho }_{{\text{s}}}})}_{{ij}}}{{\nabla }_{i}}{{({{v}_{{\text{s}}}})}_{j}} + {{({{\rho }_{{\text{n}}}})}_{{ij}}}{{\nabla }_{i}}{{\dot {u}}_{j}} = 0,$$

(3)

$$\frac{{\partial {{{({{v}_{{\text{s}}}})}}_{i}}}}{{\partial t}} + {{\nabla }_{i}}\delta {{\mu }_{l}} = 0,$$

(4)

$$\begin{gathered} (\rho _{{\text{a}}}^{{(0)}}{{\delta }_{{ij}}} + {{({{\rho }_{{\text{n}}}})}_{{ij}}}){{{\ddot {u}}}_{j}} + {{({{\rho }_{{\text{s}}}})}_{{ij}}}{{({{{\dot {v}}}_{s}})}_{j}} \\ + \;{{\nabla }_{i}}\delta p - {{\nabla }_{j}}\delta {{\sigma }_{{ij}}} = 0, \\ \end{gathered} $$

(5)

where $\delta s = s - {{s}^{{(0)}}}$, $\delta {{\rho }_{l}} = {{\rho }_{l}} - \rho _{l}^{{(0)}}$, and δρ_a = ρ_a – $\rho _{{\text{a}}}^{{(0)}}$ are small deviations of the entropy, density of ³He, and density of the aerogel from the equilibrium values, respectively; and $\delta {{\mu }_{l}}$, $\delta p$, and $\delta {{\sigma }_{{ij}}}$ are the changes in the chemical potential of the liquid per particle, pressure, and stress tensor, respectively. The presence of the stress tensor of the aerogel in the law of conservation of the total momentum of the system is an additional feature of the considered system. If the pressure is defined as a change in the total energy of the composite system under the variation of its volume, this stress tensor should refer to the elastic energy independent of a change in the volume of the system. Since the change in the volume is determined by the divergence of the displacement vector, to exclude the mentioned terms, ${{\sigma }_{{ii}}} = 0$ should be set.

To close the system, it is necessary to express $\delta {{\mu }_{l}}$, $\delta p$, and $\delta {{\sigma }_{{ij}}}$ in terms of small deviations of the introduced hydrodynamic variables. To do this, the energy per unit volume is expanded in relative deviations from the equilibrium value, disregarding the kinetic energy, up to the second order terms:

$$\delta \varepsilon = \varepsilon - {{\varepsilon }_{0}} = \frac{{\rho _{l}^{{(0)}}c_{{{\text{l1}}}}^{2}}}{2}{{\left( {\frac{{\delta {{\rho }_{l}}}}{{\rho _{l}^{{(0)}}}}} \right)}^{2}} + [{{\rho }^{{(0)}}}c_{{{\text{al}}}}^{2}]\frac{{\delta {{\rho }_{{\text{a}}}}\delta {{\rho }_{l}}}}{{{{{({{\rho }^{{(0)}}})}}^{2}}}}$$

$$\begin{gathered} + \;(\rho _{l}^{{(0)}}{{({{c}_{{{\text{ul}}}}})}^{2}}){{{\tilde {u}}}_{{zz}}}\frac{{\delta {{\rho }_{l}}}}{{\rho _{l}^{{(0)}}}} + \frac{{\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a1}}}}^{2}}}{2}{{\left( {\frac{{\delta {{\rho }_{{\text{a}}}}}}{{\rho _{{\text{a}}}^{{(0)}}}}} \right)}^{2}} \\ + \;\{ \rho _{{\text{a}}}^{{(0)}}c_{{{\text{a3}}}}^{2}\} {{{\tilde {u}}}_{{zz}}}\frac{{\delta {{\rho }_{{\text{a}}}}}}{{\rho _{{\text{a}}}^{{(0)}}}} + \rho _{l}^{{(0)}}c_{{{\text{ls}}}}^{2}\frac{{\delta {{\rho }_{l}}\delta s}}{{\rho _{l}^{{(0)}}{{s}^{{(0)}}}}} + \rho _{{\text{a}}}^{{(0)}}c_{{{\text{as}}}}^{2}\frac{{\delta {{\rho }_{{\text{a}}}}\delta s}}{{\rho _{{\text{a}}}^{{(0)}}{{s}^{{(0)}}}}} \\ \end{gathered} $$

(6)

$$ + \;\frac{{\rho _{l}^{{(0)}}c_{{{\text{l2}}}}^{2}}}{2}{{\left( {\frac{{\delta s}}{{{{s}^{{(0)}}}}}} \right)}^{2}} + \rho _{{\text{a}}}^{{(0)}}c_{{{\text{us}}}}^{2}\frac{{\delta s}}{{{{s}^{{(0)}}}}} + {{\mu }_{{ijkl}}}\frac{{{{{\tilde {u}}}_{{ij}}}{{{\tilde {u}}}_{{kl}}}}}{2},$$

where the subscripts a and l mark quantities for the aerogel and ³He, respectively; ${{\tilde {u}}_{{ij}}} = {{u}_{{ij}}} - \frac{1}{3}{{u}_{{ll}}}{{\delta }_{{ij}}}$; the z axis is directed along the anisotropy axis of the aerogel; ${{\rho }^{{(0)}}} = \rho _{{\text{a}}}^{{(0)}} + \rho _{l}^{{(0)}}$; and the tensors ${{(\rho _{{\text{s}}}^{{(0)}})}_{{ij}}}$ and ${{\mu }_{{ijkl}}}$ are given by the expressions

$${{({{\rho }_{{\text{s}}}})}_{{ij}}} = \rho _{{\text{s}}}^{ \bot }{{\delta }_{{ij}}} + (\rho _{{\text{s}}}^{\parallel } - \rho _{{\text{s}}}^{ \bot }){{\hat {z}}_{i}}{{\hat {z}}_{j}},\quad \rho _{{\text{s}}}^{\parallel } > \rho _{{\text{s}}}^{ \bot },$$

(7)

$${{\mu }_{{ijkl}}} = \frac{{\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a2}}}}^{2}}}{2}\left( {{{\delta }_{{ik}}}{{\delta }_{{jl}}} + {{\delta }_{{il}}}{{\delta }_{{jk}}} - \frac{2}{3}{{\delta }_{{ij}}}{{\delta }_{{kl}}}} \right)$$

$$\begin{gathered} + \;\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a4}}}}^{2}\left( {\frac{1}{4}} \right.[{{\delta }_{{ik}}}{{{\hat {z}}}_{j}}{{{\hat {z}}}_{l}} + {{\delta }_{{jl}}}{{{\hat {z}}}_{i}}{{{\hat {z}}}_{k}} \\ + \;{{\delta }_{{jk}}}{{{\hat {z}}}_{i}}{{{\hat {z}}}_{l}} + {{\delta }_{{il}}}{{{\hat {z}}}_{j}}{{{\hat {z}}}_{k}}] - \left. {{{{\hat {z}}}_{i}}{{{\hat {z}}}_{j}}{{{\hat {z}}}_{k}}{{{\hat {z}}}_{{\begin{subarray}{l} l \\ {\kern 1pt} \end{subarray}} }}} \right) \\ \end{gathered} $$

(8)

$$ + \;\rho _{{\text{a}}}^{{(0)}}(c_{{{\text{a5}}}}^{2} + c_{{{\text{a4}}}}^{2})\left( {{{{\hat {z}}}_{i}}{{{\hat {z}}}_{j}} - \frac{1}{3}{{\delta }_{{ij}}}} \right)\left( {{{{\hat {z}}}_{k}}{{{\hat {z}}}_{l}} - \frac{1}{3}{{\delta }_{{kl}}}} \right);$$

c_a1, c_l1, etc., are the phenomenological coefficients with a dimension of velocity including the speeds of the first and second sounds in superfluid ³He c_l1 and c_l2, respectively; the speeds of the ith sound in the aerogel c_ai determined by its elastic coefficients; the velocities c_as, c_ls, and c_us associated with the thermal expansion effect in the aerogel and ³He; and the coefficients c_al and c_ul describing the interaction between the aerogel and ³He that are the most interesting for the problem under consideration. Since the number of variables is large, conditions of thermodynamic stability of the system are not considered below; i.e., the consideration below concerns the region of the parameters where the above quadratic form is positive definite.

Several remarks are in order concerning values of the phenomenological coefficients in the expansion of the energy. The density of ³He in the systems under consideration is on the order of the density of the aerogel; i.e., ρ_a ~ ρ_l. The speed of first sound in ³He is much higher than the speeds of sound in the aerogel; i.e., c_l1 ~ 300 m/s ≫ c_ai. The speed of second sound in superfluid Fermi systems is also very low. The elastic characteristics of nematic aerogels have not yet been systematically measured. However, some relations between the phenomenological coefficients c_ai can be assumed: the largest coefficient is c_a5 because it determines the elasticity of the system along the z axis coinciding with the direction of the strands of the aerogel. It can be accepted that velocities associated with the thermal expansion effect are much lower than the speed of first sound and all phenomenological velocities in the aerogel. Finally, the velocities describing the interaction of the aerogel with ³He should be much lower than the speeds of first sound because of a low concentration of impurities. Summarizing the aforesaid, we can confirm that the speed of first sound in the system under consideration is much higher than all other velocities.

First, using the above quadratic form, we obtain exact expressions for small variations of the chemical potential of the liquid, pressure, and stress tensor. These expressions can then be simplified using the above quantitative relations between the phenomenological coefficients. By definition,

$$\begin{gathered} \delta {{\mu }_{l}} = \frac{{\partial \mu _{l}^{{(0)}}}}{{\partial {{\rho }_{l}}}}\delta {{\rho }_{l}} + \frac{{\partial \mu _{l}^{{(0)}}}}{{\partial {{\rho }_{{\text{a}}}}}}\delta {{\rho }_{{\text{a}}}} + \frac{{\partial \mu _{l}^{{(0)}}}}{{\partial {{{\tilde {u}}}_{{ij}}}}}\delta {{{\tilde {u}}}_{{ij}}} + \frac{{\partial \mu _{l}^{{(0)}}}}{{\partial s}}\delta s \\ = \frac{{\partial \delta \varepsilon }}{{\partial \delta {{\rho }_{l}}}} = c_{{{\text{l1}}}}^{2}\frac{{\delta {{\rho }_{l}}}}{{\rho _{l}^{{(0)}}}} + c_{{{\text{al}}}}^{2}\frac{{\delta {{\rho }_{{\text{a}}}}}}{{{{\rho }^{{(0)}}}}} + c_{{{\text{ul}}}}^{2}{{{\tilde {u}}}_{{zz}}} + c_{{{\text{ls}}}}^{2}\frac{{\delta s}}{{{{s}^{{(0)}}}}}. \\ \end{gathered} $$

(9)

Since

$$\frac{{\delta s}}{{{{s}^{{(0)}}}}} = \frac{{\delta {{\rho }_{{\text{a}}}}}}{{\rho _{{\text{a}}}^{{(0)}}}} = - {{u}_{{ll}}}$$

(10)

according to Eqs. (1) and (2), Eq. (9) can be simplified to the form

$$\delta {{\mu }_{l}} = c_{{{\text{l1}}}}^{2}\frac{{\delta {{\rho }_{l}}}}{{\rho _{l}^{{(0)}}}} + c_{{{\text{ul}}}}^{2}{{u}_{{zz}}} - \tilde {c}_{{{\text{ls}}}}^{2}{{u}_{{ll}}},$$

(11)

where

$$\tilde {c}_{{{\text{ls}}}}^{2} = c_{{{\text{al}}}}^{2} + c_{{{\text{ls}}}}^{2} + \frac{1}{3}c_{{{\text{ul}}}}^{2}.$$

(12)

In the linear approximation, the variation of the pressure is given by the formula

$$\delta p = {{s}^{{(0)}}}\delta T + \rho _{l}^{{(0)}}\delta {{\mu }_{l}} + \rho _{{\text{a}}}^{{(0)}}\delta {{\mu }_{{\text{a}}}}.$$

(13)

A similar algebra for $\delta T$, $\delta {{\mu }_{{\text{a}}}}$, and $\delta {{\sigma }_{{ij}}}$ gives the following expressions for the variation of the pressure and stress tensor:

$$\delta \tilde {p} = \tilde {c}_{{{\text{l1}}}}^{2}\delta {{\rho }_{l}} + \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a3}}}}^{2}{{u}_{{zz}}} - \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a1}}}}^{2}{{u}_{{ll}}},$$

(14)

$$\begin{gathered} \delta {{{\tilde {\sigma }}}_{{ij}}} = \rho _{{\text{a}}}^{{(0)}}c_{{{\text{a2}}}}^{2}{{u}_{{ij}}} + \rho _{{\text{a}}}^{{(0)}}\frac{{c_{{{\text{a4}}}}^{2}}}{2}(\hat {z}_{i}^{{(0)}}{{u}_{{zj}}} + \hat {z}_{j}^{{(0)}}{{u}_{{zi}}}) \\ + \;\left( {\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a5}}}}^{2}{{u}_{{zz}}} + c_{{{\text{ul}}}}^{2}\delta {{\rho }_{l}} - \rho _{{\text{a}}}^{0}\tilde {c}_{{{\text{us}}}}^{2}{{u}_{{ll}}}} \right){{{\hat {z}}}_{i}}{{{\hat {z}}}_{j}}, \\ \end{gathered} $$

(15)

where the second and third terms on the right-hand side of Eq. (14) include the coefficient of the first term in Eq. (5) and

$$\tilde {c}_{{{\text{l1}}}}^{2} = c_{{{\text{l1}}}}^{2} + c_{{{\text{al}}}}^{2}\frac{{\rho _{l}^{{(0)}}}}{{{{\rho }^{{(0)}}}}} + c_{{{\text{ls}}}}^{2} + \frac{1}{3}c_{{{\text{ul}}}}^{2},$$

(16)

$$\rho _{{\text{a}}}^{0}\tilde {c}_{{{\text{a3}}}}^{2} = \rho _{{\text{a}}}^{{(0)}}\left( {c_{{{\text{a3}}}}^{2} + \frac{1}{3}[c_{{{\text{a4}}}}^{2} + c_{{{\text{a5}}}}^{2}]} \right) + \rho _{l}^{{(0)}}c_{{{\text{ul}}}}^{2} + {{\rho }^{{(0)}}}c_{{{\text{us}}}}^{2},$$

(17)

$$\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a1}}}}^{2} = \rho _{{\text{a}}}^{{(0)}}c_{{{\text{a1}}}}^{2} + \rho _{{\text{a}}}^{{(0)}}c_{{{\text{al}}}}^{2}\frac{{\rho _{{\text{a}}}^{{(0)}}}}{{{{\rho }^{{(0)}}}}} + 2\rho _{{\text{a}}}^{{(0)}}c_{{{\text{as}}}}^{2} + \rho _{l}^{{(0)}}c_{{{\text{l2}}}}^{2}$$

$$ + \;\rho _{l}^{{(0)}}c_{{{\text{ls}}}}^{2} + \frac{2}{3}\rho _{{\text{a}}}^{{(0)}}c_{{{\text{us}}}}^{2} + \frac{1}{3}\rho _{l}^{{(0)}}c_{{{\text{ul}}}}^{2}$$

(18)

$$ - \;\frac{1}{3}\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a2}}}}^{2} - \frac{2}{3}\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a3}}}}^{2} + \frac{1}{9}{{\rho }_{{\text{a}}}}(c_{{{\text{a4}}}}^{2} + c_{{{\text{a5}}}}^{2}),$$

$$\tilde {c}_{{{\text{us}}}}^{2} = c_{{{\text{us}}}}^{2}\frac{{{{\rho }^{{(0)}}}}}{{\rho _{{\text{a}}}^{{(0)}}}} + c_{{{\text{a3}}}}^{2} + \frac{1}{3}\left( {{{c}_{{{\text{a}}{{{\text{4}}}^{2}}}}} + c_{{{\text{a5}}}}^{2}} \right).$$

(19)

According to the above estimates, we accept below

$$\tilde {c}_{{{\text{l1}}}}^{2} \approx c_{{{\text{l1}}}}^{2}.$$

(20)

3 DISPERSION EQUATION

To solve the system of Eqs. (3)–(5), we use the definition of the potentiality of the superfluid flow in the polar phase; i.e., ${{({{v}_{s}})}_{i}} = {{\nabla }_{i}}\delta \varphi$ ($\hbar {\text{/}}2m = 1$). Then, Eq. (5) is simplified to the form

$$\frac{{\partial \delta \varphi }}{{\partial t}} + \delta {{\mu }_{l}} = 0.$$

(21)

The solution of equations is sought in the form of a periodic function $\sim {\kern 1pt} {{e}^{{ - i\omega t + i{\mathbf{kr}}}}}$. Excluding the variable δρ_l from Eqs. (3) and (21) and making trivial transformations, we obtain the following expressions for $\delta \varphi$, $\delta p$, and $\delta {{\sigma }_{{ij}}}$ written as functions of the displacement ${{u}_{i}}$:

$$\begin{gathered} \delta \varphi = \omega {{k}_{i}}{{(\delta \varphi )}_{{ij}}}{{u}_{j}} \\ = \omega {{k}_{i}}\left\{ {{{{(\delta \varphi )}}_{ \bot }}{{\delta }_{{ij}}} + [(\delta \varphi {{)}_{\parallel }} - {{{(\delta \varphi )}}_{ \bot }}]{{{\hat {z}}}_{i}}{{{\hat {z}}}_{j}}} \right\}{{u}_{j}}, \\ \end{gathered} $$

(22)

$$\begin{gathered} \delta \tilde {p} = i{{k}_{i}}{{(\delta p)}_{{ij}}}{{u}_{j}} \\ = i{{k}_{i}}\left\{ {{{{(\delta p)}}_{ \bot }}{{\delta }_{{ij}}} + [(\delta p{{)}_{\parallel }} - {{{(\delta p)}}_{ \bot }}]{{{\hat {z}}}_{i}}{{{\hat {z}}}_{j}}} \right\}{{u}_{j}}, \\ \end{gathered} $$

(23)

$$\delta {{\tilde {\sigma }}_{{ij}}} = i\delta {{\alpha }_{{ijlm}}}{{k}_{l}}{{u}_{m}}$$

(24)

$$\begin{gathered} = i\left( {\rho _{{\text{a}}}^{{(0)}}\frac{{c_{{{\text{a2}}}}^{2}}}{2}} \right.[{{\delta }_{{im}}}{{\delta }_{{jl}}} + {{\delta }_{{il}}}{{\delta }_{{jm}}} \\ + \;\frac{{\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a4}}}}^{2}}}{4}[{{{\hat {z}}}_{i}}{{{\hat {z}}}_{m}}{{\delta }_{{jl}}} + {{{\hat {z}}}_{j}}{{{\hat {z}}}_{m}}{{\delta }_{{il}}} + {{{\hat {z}}}_{j}}{{{\hat {z}}}_{l}}{{\delta }_{{im}}} + {{{\hat {z}}}_{i}}{{{\hat {z}}}_{l}}{{\delta }_{{jm}}}] \\ \end{gathered} $$

$$ + \;{{\hat {z}}_{i}}{{\hat {z}}_{j}}\left. {{{{\left\{ {{{{(\delta \alpha )}}_{ \bot }}{{\delta }_{{lm}}} + [(\delta \alpha {{)}_{\parallel }} - {{{(\delta \alpha )}}_{ \bot }}]{{{\hat {z}}}_{l}}{{{\hat {z}}}_{m}}} \right\}}}_{{\begin{subarray}{l} {\kern 1pt} \\ {\kern 1pt} \end{subarray}} }}} \right){{k}_{l}}{{u}_{m}},$$

where

$${{(\delta \varphi )}_{ \bot }} = - \frac{{\tilde {c}_{{{\text{ls}}}}^{2}\rho _{l}^{{(0)}} + c_{{{\text{l1}}}}^{2}\rho _{{\text{n}}}^{ \bot }}}{{{{\omega }^{2}}\rho _{l}^{{(0)}} - {{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}},$$

(25)

$${{(\delta \varphi )}_{\parallel }} - {{(\delta \varphi )}_{ \bot }} = \frac{{c_{{{\text{ul}}}}^{2}\rho _{l}^{{(0)}} - c_{{{\text{l1}}}}^{2}[\rho _{{\text{n}}}^{\parallel } - \rho _{{\text{n}}}^{ \bot }]}}{{{{\omega }^{2}}\rho _{l}^{{(0)}} - {{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}},$$

(26)

$${{(\delta p)}_{ \bot }} = \frac{1}{{{{\omega }^{2}}\rho _{l}^{{(0)}} - {{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}}$$

$$ \times \;( - \rho _{l}^{{(0)}}{{\omega }^{2}}[\rho _{{\text{n}}}^{ \bot }c_{{{\text{l1}}}}^{2} + \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a1}}}}^{2}]$$

(27)

$$ + \;{{({{\rho }_{{\text{s}}}})}_{{ij}}}{{k}_{i}}{{k}_{j}}[\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a1}}}}^{2} - \rho _{l}^{{(0)}}\tilde {c}_{{{\text{ls}}}}^{2}]c_{{{\text{l1}}}}^{2}),$$

$${{(\delta p)}_{\parallel }} - {{(\delta p)}_{ \bot }} = \frac{1}{{{{\omega }^{2}}\rho _{l}^{{(0)}} - {{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}}$$

$$ \times \;({{\omega }^{2}}\rho _{l}^{{(0)}}[\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a3}}}}^{2} - [\rho _{{\text{n}}}^{\parallel } - \rho _{{\text{n}}}^{ \bot }]c_{{{\text{l1}}}}^{2}]$$

(28)

$$ - \;{{({{\rho }_{{\text{s}}}})}_{{ij}}}{{k}_{i}}{{k}_{j}}[\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a3}}}}^{2} - \rho _{l}^{{(0)}}c_{{{\text{ul}}}}^{2}]c_{{{\text{l1}}}}^{2}),$$

$${{(\delta \alpha )}_{ \bot }} = - \frac{1}{{{{\omega }^{2}}\rho _{l}^{{(0)}} - {{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}}$$

$$ \times \;(\rho _{l}^{{(0)}}{{\omega }^{2}}[\rho _{{\text{n}}}^{ \bot }c_{{{\text{ul}}}}^{2} + \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{us}}}}^{2}]$$

(29)

$$ - \;{{({{\rho }_{{\text{s}}}})}_{{ij}}}{{k}_{i}}{{k}_{j}}[\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{us}}}}^{2}c_{{{\text{l1}}}}^{2} - \rho _{l}^{{(0)}}\tilde {c}_{{{\text{ls}}}}^{2}c_{{{\text{ul}}}}^{2}]),$$

$${{(\delta \alpha )}_{\parallel }} - {{(\delta \alpha )}_{ \bot }} = \frac{1}{{{{\omega }^{2}}\rho _{l}^{{(0)}} - {{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}}$$

$$ \times \;({{\omega }^{2}}\rho _{l}^{{(0)}}[\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a5}}}}^{2} - [\rho _{{\text{n}}}^{\parallel } - \rho _{{\text{n}}}^{ \bot }]c_{{{\text{ul}}}}^{2}]$$

(30)

$$ - \;{{({{\rho }_{{\text{s}}}})}_{{ij}}}{{k}_{i}}{{k}_{j}}[\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a5}}}}^{2}c_{{{\text{l1}}}}^{2} - \rho _{l}^{{(0)}}c_{{{\text{ul}}}}^{4}]).$$

Using these expressions and the introduced notation, we rewrite the resulting equation for the displacement vector u in the form

$$\begin{gathered} \text{[} - {{\omega }^{2}}\{ \rho _{{\text{a}}}^{{(0)}}{{\delta }_{{im}}} + {{({{\rho }_{{\text{n}}}})}_{{im}}} - {{({{\rho }_{{\text{s}}}})}_{{ij}}}{{(\delta \varphi )}_{{lm}}}{{k}_{j}}{{k}_{l}}\} \\ + \;\{ (\delta \alpha {{)}_{{ijlm}}} - {{\delta }_{{il}}}{{(\delta p)}_{{jm}}}\} {{k}_{j}}{{k}_{l}}]{{u}_{m}} = 0. \\ \end{gathered} $$

(31)

The condition of consistency of three linear equations gives the dispersion equation for the frequencies of oscillations in the form

$$\begin{gathered} det( - {{\omega }^{2}}\{ \rho _{{\text{a}}}^{{(0)}}{{\delta }_{{im}}} + {{({{\rho }_{{\text{n}}}})}_{{im}}} - {{({{\rho }_{{\text{s}}}})}_{{ij}}}{{(\delta \varphi )}_{{lm}}}{{k}_{j}}{{k}_{l}}\} \\ + \;\{ (\delta \alpha {{)}_{{ijlm}}} - {{\delta }_{{il}}}{{(\delta p)}_{{jm}}}\} {{k}_{j}}{{k}_{l}}) = 0. \\ \end{gathered} $$

(32)

This equation is generally a fourth order equation for the frequency squared and, correspondingly, gives four vibrational modes for each direction of the wave vector. The fourth vibrational mode should obviously appear at the point of the superfluid transition in the aerogel and be an analog of second sound in the system under consideration. The existence of three vibrational modes above the transition point is due to the anisotropic elastic properties of the aerogel.

4 LOW-FREQUENCY MODES

The exact solution of Eq. (32) is too lengthy. We consider only several simple limits corresponding to recent experiments [8]. Resonances observed in oscillating experiments with the nematic aerogel in ³He have frequencies of about 1 kHz. Since the characteristic wavelengths of excited waves are determined by the sizes of the aerogel about $1$ mm, the first sound in ³He inside the aerogel is not excited in the discussed experiments. For this reason, we solve Eq. (32) only for low-frequency oscillating modes of the system, i.e., taking into account the small parameter ${{\omega }^{2}}{\text{/}}(c_{{{\text{l1}}}}^{2}{{k}^{2}})$ in this equation. Furthermore, since the speed of sound in ³He is about 300 m/s and the superfluid density is measured with an accuracy limited by the condition $\frac{{{{\rho }_{{\text{s}}}}}}{{\rho _{l}^{{(0)}}}}{{ > 10}^{{ - 4}}}$, the more stringent condition ${{\omega }^{2}} \ll \frac{{{{\rho }_{{\text{s}}}}}}{{\rho _{l}^{{(0)}}}}{{k}^{2}}c_{{{\text{l1}}}}^{2}$ is satisfied in the entire available temperature range. Thus, in the zeroth order in the mentioned small parameters, the first term and the ratios of all velocities to the speed of first sound c_l1 in the denominators of the expressions for $\delta {{\varphi }_{{ \bot ,\parallel }}}$, $\delta {{p}_{{ \bot ,\parallel }}}$, and $\delta {{\alpha }_{{ \bot ,\parallel }}}$ can be neglected. In this approximation, the components of the tensors ${{(\delta \varphi )}_{{ij}}}$, ${{(\delta p)}_{{ij}}}$, and ${{(\delta \alpha )}_{{ijkl}}}$ have the very simple form

$${{(\delta \varphi )}_{ \bot }} = \frac{{\rho _{{\text{n}}}^{ \bot }}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}},$$

$${{(\delta \varphi )}_{\parallel }} - {{(\delta \varphi )}_{ \bot }} = \frac{{[\rho _{{\text{n}}}^{\parallel } - \rho _{{\text{n}}}^{ \bot }]}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}},$$

$${{(\delta p)}_{ \bot }} = {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}\rho _{n}^{ \bot }}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}} - \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a1}}}}^{2} + \rho _{l}^{{(0)}}\tilde {c}_{{{\text{ls}}}}^{2},$$

$${{(\delta p)}_{\parallel }} - {{(\delta p)}_{ \bot }} = {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}[\rho _{{\text{n}}}^{\parallel } - \rho _{{\text{n}}}^{ \bot }]}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}} + \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a3}}}}^{2} - \rho _{l}^{{(0)}}c_{{{\text{ul}}}}^{2},$$

$${{(\delta \alpha )}_{ \bot }} = - \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{us}}}}^{2},$$

$${{(\delta \alpha )}_{\parallel }} - {{(\delta \alpha )}_{ \bot }} = \rho _{{\text{a}}}^{{(0)}}c_{{{\text{a5}}}}^{2}.$$

We consider the propagation of waves in the aerogel along and across the anisotropy axis of the aerogel. In the former case where ${{k}_{{x,y}}} = 0$, two frequencies of vibrations for two transverse (${{u}_{z}} = 0$) modes and one longitudinal (${{u}_{z}} \ne 0$) mode are obtained:

$${{(\omega _{{1,2}}^{z})}^{2}} = \frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{{\text{a}}}^{0} + \rho _{{\text{n}}}^{ \bot }}}\frac{{2c_{{{\text{a2}}}}^{2} + c_{{{\text{a4}}}}^{2}}}{4}k_{z}^{2},$$

(33)

$${{(\omega _{3}^{z})}^{2}} = \frac{{\rho _{l}^{{(0)}}\rho _{{\text{s}}}^{\parallel }}}{{\rho _{{\text{a}}}^{0}\rho _{{\text{s}}}^{\parallel } + \rho _{l}^{{(0)}}\rho _{{\text{n}}}^{\parallel }}}\tilde {c}_{{{\text{a5}}}}^{2}k_{z}^{2},$$

(34)

where $\tilde {c}_{{{\text{a5}}}}^{2}\;\, = \;\,[\tilde {c}_{{{\text{a1}}}}^{2}\; + \;c_{{{\text{a2}}}}^{2} - \tilde {c}_{{{\text{a3}}}}^{2}\; + \;c_{{{\text{a4}}}}^{2}\; + \;c_{{{\text{a5}}}}^{2}\; - \;\tilde {c}_{{{\text{us}}}}^{2}]\frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{l}^{{(0)}}}}\;\, +$ $c_{{{\text{ul}}}}^{2} - \tilde {c}_{{{\text{ls}}}}^{2}$. The first oscillating mode obviously corresponds to transverse oscillations of the aerogel and the normal component of ³He, which propagate along the z axis. This solution exists in both the normal and superfluid phases and is due exclusively to the elasticity of the aerogel. The second vibrational mode is an analog of second sound in the superfluid system. Indeed, in the limit of zero velocities associated with the aerogel and zero density of aerogel, the conventional expression for the frequency of second sound in the superfluid system is obtained:

$${{(\omega _{3}^{z})}^{2}} \to \frac{{\rho _{{\text{s}}}^{\parallel }}}{{\rho _{{\text{n}}}^{\parallel }}}c_{{{\text{l2}}}}^{2}k_{z}^{2}.$$

(35)

In is noteworthy that the propagation velocity of oscillations of this mode is now determined only by the elasticity of the aerogel along the z axis because of the interaction with the aerogel.

We obtain the following results for oscillations propagating in the directions perpendicular to the z axis:

$${{(\omega _{1}^{{xy}})}^{2}} = \frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{{\text{a}}}^{0} + \rho _{{\text{n}}}^{\parallel }}}\frac{{2c_{{{\text{a2}}}}^{2} + c_{{{\text{a4}}}}^{2}}}{4}(k_{x}^{2} + k_{y}^{2}),$$

(36)

$${{(\omega _{2}^{{xy}})}^{2}} = \frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{{\text{a}}}^{0} + \rho _{{\text{n}}}^{ \bot }}}\frac{{c_{{{\text{a}}2}}^{2}}}{2}(k_{x}^{2} + k_{y}^{2}),$$

(37)

$$\begin{gathered} {{(\omega _{3}^{{xy}})}^{2}} = \frac{{\rho _{l}^{{(0)}}\rho _{{\text{s}}}^{ \bot }}}{{\rho _{{\text{a}}}^{0}\rho _{{\text{s}}}^{ \bot } + \rho _{l}^{{(0)}}\rho _{{\text{n}}}^{ \bot }}} \\ \times \;\left( {[\tilde {c}_{{{\text{a1}}}}^{2} + c_{{{\text{a2}}}}^{2}]\frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{l}^{{(0)}}}} - \tilde {c}_{{{\text{ls}}}}^{2}} \right)(k_{x}^{2} + k_{y}^{2}). \\ \end{gathered} $$

(38)

The first oscillating mode is similar to the first two modes ($\omega _{{1,2}}^{z}$) found above, but it refers to the z component of the displacement vector. The frequencies of the modes is different because the normal component of the density of the polar phase of superfluid ³He is anisotropic. The second transverse mode is in turn due to the anisotropic elastic properties of the aerogel. Finally, the third vibrational mode includes the joint oscillations of the normal component of ³He and the aerogel with respect to the superfluid component; i.e., it is also an analog of second sound but for vibrations propagating in the transverse direction.

The spectrum of eigenmodes of the system depends on the boundary conditions on the surface of the aerogel. In the considered experimental situation where the rectangular parallelepiped aerogel is in a cell and is surrounded by ³He, it is additionally necessary to solve hydrodynamic equations for the corresponding superfluid phase outside the aerogel with the condition of absence of current at infinity. This problem is qualitatively discussed in the next section.

5 SHEAR OSCILLATIONS

We now approximately consider oscillations where all components of the displacement vector and the wave vector are nonzero. It is substantial that the aerogel is surrounded by superfluid ³He. Simple estimates can demonstrate that shear oscillations can be excited in this case in the system. The spatial part of the solution inside the aerogel is sought in the form

$$\begin{gathered} {{u}_{x}} \\ = u_{x}^{{(0)}}\sin ({{k}_{x}}x + {{\gamma }_{x}})\cos ({{k}_{y}}y + {{\gamma }_{y}})\cos ({{k}_{z}}z + {{\gamma }_{z}}), \\ \end{gathered} $$

(39)

$$\begin{gathered} {{u}_{y}} \\ = u_{y}^{{(0)}}\cos ({{k}_{x}}x + {{\gamma }_{x}})\sin ({{k}_{y}}y + {{\gamma }_{y}})\cos ({{k}_{z}}z + {{\gamma }_{z}}), \\ \end{gathered} $$

(40)

$$\begin{gathered} {{u}_{z}} \\ = u_{z}^{{(0)}}\cos ({{k}_{x}}x + {{\gamma }_{x}})\cos ({{k}_{y}}y + {{\gamma }_{y}})\sin ({{k}_{z}}z + {{\gamma }_{z}}). \\ \end{gathered} $$

(41)

Oscillations of the aerogel can excite waves of the first and second sounds. Since the speed of second sound is much lower than the elastic velocities of the aerogel, second sound will be emitted to the environment, making a contribution to the damping of eigenmodes of the system. On the contrary, the speed of first sound is much higher than speeds of sound in the aerogel; as a result, waves of the first sound are damped far from the edge of the aerogel. Indeed, the square of the wave vector for oscillations of the first sound outside the aerogel has the form

$${{(k_{1}^{{{\text{out}}}})}^{2}} = \frac{{{{\omega }^{2}}}}{{c_{{{\text{l1}}}}^{2}}},$$

(42)

where ω is the frequency of eigenmodes of the system (aerogel and ³He). The wavelength of the first sound even for the highest frequencies of oscillations of about 1.6 kHz is approximately 20–25 cm, which is much larger than the dimensions of the sample. The solution for the normal component of the displacement in ³He near the (x, z) plane separating the aerogel ($y < 0$) and liquid ($y > 0$) has the approximate form

$${{u}_{y}} \approx u_{y}^{{(0)}}\sin {{\gamma }_{y}}{{e}^{{ - k_{y}^{{{\text{out}}}}y}}}\cos ({{k}_{x}}x)\cos ({{k}_{z}}z),$$

(43)

where $k_{y}^{{{\text{out}}}} = \sqrt {k_{x}^{2} + k_{z}^{2} - {{{(k_{1}^{{{\text{out}}}})}}^{2}}}$ ≈ $\sqrt {k_{x}^{2} + k_{z}^{2}}$. The components of the momentum flux tensor ${{\Pi }_{{ij}}}{{n}_{j}}$, in particular, the component ${{\Pi }_{{yy}}}$, should be continuous at the boundary of the aerogel specified by the normal ${{n}_{i}}$. Since oscillations of the pressure in the second sound in the superfluid liquid surrounding the aerogel are very small, the main contribution to $\Pi _{{yy}}^{{{\text{out}}}}$ comes from the damping wave of the first sound:

$$\Pi _{{yy}}^{{{\text{out}}}} \approx \rho _{l}^{{(0)}}c_{{{\text{l1}}}}^{2}{{\partial }_{i}}{{u}_{i}} = \frac{{\rho _{l}^{{(0)}}{{\omega }^{2}}}}{{k_{y}^{{{\text{out}}}}}}{{u}_{y}}.$$

(44)

Inside the aerogel,

$$\Pi _{{yy}}^{{{\text{in}}}} \approx \rho _{{\text{a}}}^{{(0)}}c_{{{\text{a}}y}}^{2}{{\partial }_{y}}{{u}_{y}} - {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}\rho _{{\text{n}}}^{ \bot }}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}k_{i}^{{{\text{in}}}}k_{j}^{{{\text{in}}}}}}{{\partial }_{i}}{{u}_{i}},$$

(45)

where $c_{{{\text{a}}y}}^{2} = \tilde {c}_{{{\text{a1}}}}^{2} + c_{{{\text{a2}}}}^{2}$ is the longitudinal velocity of sound along the y direction in the aerogel. Near T_c when ρ_s ≪ρ_n, we set $\rho _{{\text{a}}}^{{(0)}}c_{{{\text{a}}y}}^{2} \ll {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}\rho _{{\text{n}}}^{ \bot }}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}}$ (we below determine the region of aerogel parameters where this condition is applicable); hence, the first term in Eq. (45) can be neglected. From the condition $\Pi _{{yy}}^{{{\text{in}}}}$ = $\Pi _{{yy}}^{{{\text{out}}}}$ at the boundary, we obtain the relation

$$(u_{i}^{{(0)}}k_{i}^{{{\text{in}}}}) = - \frac{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}k_{i}^{{{\text{in}}}}k_{j}^{{{\text{in}}}}}}{{\rho _{{\text{n}}}^{ \bot }k_{y}^{{{\text{in}}}}k_{y}^{{{\text{out}}}}}}(u_{y}^{{(0)}}k_{y}^{{{\text{in}}}})\tan {{\gamma }_{y}}.$$

(46)

First, since $k_{x}^{{{\text{in}}}}$, $k_{y}^{{{\text{in}}}}$, and $k_{y}^{{{\text{out}}}}$ have the same order of magnitude, $\frac{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}k_{i}^{{{\text{in}}}}k_{j}^{{{\text{in}}}}}}{{\rho _{{\text{n}}}^{ \bot }k_{y}^{{{\text{in}}}}k_{y}^{{{\text{out}}}}}} \sim \frac{{{{\rho }_{{\text{s}}}}}}{{{{\rho }_{{\text{n}}}}}} \ll 1$. Second, since ${{\Pi }_{{xy}}}$ is continuous, $\sin {{\gamma }_{y}} \sim \delta (\omega ){{k}_{x}} \ll 1$, where $\delta (\omega ) \sim$ 0.1 mm is the viscous penetration depth in ³He for fr-equencies of about 1 kHz. Thus, ${\text{|}}u_{y}^{{{\text{in}}}}{{k}_{y}}{\text{|}} \gg {\text{|}}{{u}_{i}}k_{i}^{{{\text{in}}}}{\text{|}}$. A similar consideration of the other side face of the aerogel (parallel to the axis of anisotropy) gives ${\text{|}}u_{x}^{{{\text{in}}}}{{k}_{x}}{\text{|}} \gg {\text{|}}{{u}_{i}}k_{i}^{{{\text{in}}}}{\text{|}}$. Below, we consider oscillations where $u_{x}^{{(0)}}$ and $u_{y}^{{(0)}}$ have the same sign (simultaneous compression or extension in side directions). The relation ${\text{|}}{{k}_{i}}{{u}_{i}}{\text{|}} \ll {\text{|}}{{k}_{z}}{{u}_{z}}{\text{|}}$ following from the additional condition $\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a5}}}}^{2} \ll {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}\rho _{{\text{n}}}^{ \bot }}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}}$is valid for such oscillations. Thus, ${{k}_{i}}{{u}_{i}} \approx 0$ can be set in the zeroth order in the ratio ρ_s/ρ_n. As a result, the considered oscillations near T_c should be purely shear because the aerogel is surrounded by an incompressible liquid. We now determine the relations between $k_{x}^{{{\text{in}}}}$, $k_{y}^{{{\text{in}}}}$, and $k_{z}^{{{\text{in}}}}$ in this type of oscillations. As mentioned above, the stiffness of the aerogel along the z axis is much higher than that in the transverse direction. Consequently, under the assumption that the longitudinal velocity of sound along the z axis in the aerogel is several times higher than the transverse one, $k_{z}^{2} \sim {{\omega }^{2}}{\text{/}}\tilde {c}_{{{\text{a5}}}}^{2} \ll k_{x}^{2}, k_{y}^{2}$ follows from the equation for ${{u}_{z}}$ (under the assumption that the resulting frequency of oscillations is determined by the transverse velocity of sound in the aerogel). The oscillations under consideration occur as bilateral compression in the transverse direction with simultaneous stretching in the longitudinal direction, conserving the total volume aerogel; i.e., they are oscillations of the shape of the aerogel.

To determine the spectrum of the system under the additional requirement ${{k}_{i}}{{u}_{i}} = 0$, ${{u}_{z}} = - \frac{{{{u}_{x}}{{k}_{x}} + {{u}_{y}}{{k}_{y}}}}{{{{k}_{z}}}}$ obtained in the zeroth approximation is substituted into the first two equations for ${{u}_{x}}$ and ${{u}_{y}}$. Thus, the effective system of equations has the form

$$\left[ { - {\kern 1pt} (\rho _{{\text{a}}}^{0} + \rho _{{\text{n}}}^{ \bot }){{\omega }^{2}} + \left( {\frac{{\rho _{{\text{a}}}^{0}c_{{{\text{a2}}}}^{2}}}{2}} \right.} \right. - \frac{{\rho _{{\text{a}}}^{0}c_{{{\text{a4}}}}^{2}}}{4}$$

$$ - \;\rho _{{\text{s}}}^{ \bot }[(\delta \varphi {{)}_{\parallel }} - {{(\delta \varphi )}_{ \bot }}]{{\omega }^{2}} + [\delta {{p}_{\parallel }} - \left. {\delta {{p}_{ \bot }}{{]}_{{\begin{subarray}{l} {\kern 1pt} \\ {\kern 1pt} \end{subarray}} }}} \right)k_{x}^{2}$$

$$ + \;\frac{{\rho _{{\text{a}}}^{0}c_{{{\text{a2}}}}^{2}}}{2}k_{y}^{2} + \left. {\left( {\frac{{\rho _{{\text{a}}}^{0}c_{{{\text{a2}}}}^{2}}}{2} + \frac{{\rho _{{\text{a}}}^{0}c_{{{\text{a4}}}}^{2}}}{4}} \right)k_{z}^{2}} \right]{{u}_{x}}$$

(47)

$$ + \;\left[ { - {\kern 1pt} \rho _{{\text{s}}}^{ \bot }[(\delta \varphi {{)}_{{\begin{subarray}{l} \parallel \\ {\kern 1pt} \end{subarray}} }}} \right. - {{(\delta \varphi )}_{ \bot }}]{\kern 1pt} {{\omega }^{2}}$$

$$ + \;\left. {\left( {\delta {{p}_{\parallel }} - \delta {{p}_{ \bot }} - \frac{{\rho _{{\text{a}}}^{0}c_{{{\text{a4}}}}^{2}}}{4}} \right)} \right]{{k}_{x}}{{k}_{y}}{{u}_{y}} = 0,$$

where the second equation is obtained from the first one by replacement of the indices $x \leftrightarrow y$. To obtain the relation between oscillations of the aerogel and the superfluid component of ³He, the expression for $(\delta {{p}_{\parallel }} - \delta {{p}_{ \bot }})$ should be written up to the first nonvanishing term in the small parameter ${{\omega }^{2}}{\text{/}}(c_{{{\text{l1}}}}^{2}{{k}^{2}})$, i.e.,

$$\begin{gathered} \delta {{p}_{\parallel }} - \delta {{p}_{ \bot }} = {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}[\rho _{{\text{n}}}^{\parallel } - \rho _{{\text{n}}}^{ \bot }]}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}} + \rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a3}}}}^{2} \\ - \;\rho _{l}^{{(0)}}c_{{{\text{ul}}}}^{2}\left( {1 + \frac{{\rho _{l}^{{(0)}}{{\omega }^{2}}}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}c_{{{\text{l1}}}}^{2}}}} \right). \\ \end{gathered} $$

(48)

Under the above assumption, the terms proportional to $k_{z}^{2}$ can be omitted in all equations. The condition of consistency of two linear equations gives two frequencies of oscillations:

$$\omega _{1}^{2} = \frac{{\rho _{{\text{a}}}^{0}}}{{{{\rho }_{{\text{a}}}} + \rho _{{\text{n}}}^{ \bot }}}\frac{{c_{{{\text{a2}}}}^{2}}}{2}(k_{x}^{2} + k_{y}^{2}),$$

(49)

$$\omega _{2}^{2} = \frac{{\rho _{{\text{a}}}^{{(0)}}\rho _{{\text{s}}}^{ \bot }(k_{x}^{2} + k_{y}^{2})c_{{{\text{a}} \bot }}^{2}}}{{\left[ {(\rho _{{\text{n}}}^{ \bot }\rho _{{\text{s}}}^{\parallel } + \rho _{{\text{a}}}^{{(0)}}\rho _{{\text{s}}}^{ \bot }) + \rho _{l}^{{(0)}}\rho _{n}^{ \bot }\frac{{c_{{{\text{ul}}}}^{2}}}{{c_{{{\text{l1}}}}^{2}}}} \right]}},$$

(50)

where $c_{{{\text{a}} \bot }}^{2} = \left( {\frac{{c_{{{\text{a2}}}}^{2}}}{2} + \left( {\tilde {c}_{{{\text{a3}}}}^{2} - \frac{{\rho _{l}^{{(0)}}}}{{\rho _{{\text{a}}}^{0}}}c_{{{\text{ul}}}}^{2}} \right) - \frac{{c_{{{\text{a4}}}}^{2}}}{4}} \right)$. The first frequency corresponds to an eigenvector in which oscillations along the x and y axes are antiphase and satisfy the relation ${{k}_{x}}{{u}_{x}} + {{k}_{y}}{{u}_{y}} = 0$. Therefore, this solution should be rejected because it does not satisfy the initial assumption. The second mode satisfying the condition ${{k}_{x}}{{u}_{x}} + {{k}_{y}}{{u}_{y}} \ne 0$ is of the most interest. After the substitution of the expression for $\tilde {c}_{{{\text{a3}}}}^{{}}$ into the formula for $c_{{{\text{a}} \bot }}^{{}}$ below Eq. (50), it is seen that the velocity ${{c}_{{{\text{a}} \bot }}}$ is independent of ${{c}_{{{\text{ul}}}}}$ and, thereby, is completely determined by the elastic properties of the aerogel. The following two asymptotic expressions can be obtained from the resulting formula:

$$\frac{{(\rho _{{\text{s}}}^{ \bot }\rho _{{\text{a}}}^{0})}}{{{{{(\rho _{l}^{{(0)}})}}^{2}}}}\frac{{c_{{{\text{a}} \bot }}^{2}}}{{c_{{{\text{ul}}}}^{2}}}c_{{{\text{l1}}}}^{2}{{k}^{2}},\quad \frac{{\langle {{\rho }_{{\text{s}}}}\rangle }}{{\rho _{l}^{{(0)}}}} \ll \frac{{c_{{{\text{ul}}}}^{2}}}{{c_{{{\text{l1}}}}^{2}}},$$

(51)

$$\frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{{\text{a}}}^{{(0)}} + {{\rho }_{n}}\frac{{\rho _{{\text{s}}}^{\parallel }}}{{\rho _{{\text{s}}}^{ \bot }}}}}c_{{{\text{a}} \bot }}^{2}{{k}^{2}},\quad \frac{{\langle {{\rho }_{{\text{s}}}}\rangle }}{{\rho _{l}^{{(0)}}}} \gg \frac{{c_{{{\text{ul}}}}^{2}}}{{c_{{{\text{l1}}}}^{2}}},$$

(52)

where $\langle {{\rho }_{{\text{s}}}}\rangle = \rho _{{\text{s}}}^{\parallel } + \frac{{\rho _{{\text{a}}}^{{(0)}}}}{{\rho _{l}^{{(0)}}}}\rho _{{\text{s}}}^{ \bot }$. At relatively low superfluid densities, Eq. (51) is proportional to $\rho _{{\text{s}}}^{ \bot }c_{1}^{2}$, which coincides with the dependence for fourth sound propagating in the direction perpendicular to the anisotropy axis of the aerogel. In the opposite limit, the asymptotic expression for the frequency squared is determined by the frequency of shear oscillations of the aerogel with the inclusion of the additional mass of ³He.

6 COMPARISON WITH EXPERIMENTAL DATA

We compare the derived dependence with experimental data in the initial segment, i.e., near the superfluid transition temperature, where the Ginzburg–Landau expansion is applicable [8] (see Fig. 1). The anisotropy of the superfluid density tensor in the Ginzburg–Landau limit is independent of the pressure, and $\rho _{{\text{s}}}^{\parallel }{\text{/}}\rho _{{\text{s}}}^{ \bot }$ = 3. In the same approximation, the superfluid density in the direction perpendicular to the orbital vector ${\mathbf{m}}$ is given by the formula

$$\rho _{{\text{s}}}^{ \bot } = \frac{{\left( {1 - \frac{T}{{{{T}_{{{\text{ca}}}}}}}} \right)}}{{{{\beta }_{{12345}}}}}\frac{{\rho _{l}^{{(0)}}}}{{\left( {1 + \frac{{F_{1}^{s}}}{3}} \right)}}.$$

(53)

Fig. 1.

(Dashed line) Schematic temperature dependence of the longitudinal oscillating mode given by Eq. (34); (○, ×, +) temperature dependences of the frequency of the second oscillating mode observed in the experiment reported in [8] at pressures of 7.1, 15.6, and 29.3 bar, respectively; and (solid lines) theoretical fits for the shear oscillating mode (50); $\rho _{{\text{s}}}^{ \bot }$ used to plot the dependences is given by Eq. (53) with ${{\beta }_{i}}$ for pure ³He.

Here, T_ca is the superfluid transition temperature to the polar phase; ${{\beta }_{{12345}}} = {{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}} + {{\beta }_{4}} + {{\beta }_{5}}$, where ${{\beta }_{i}}$ are the coefficients of the Ginzburg–Landau expansion of the free energy of ³He; and $F_{1}^{s}$ is the Landau parameter of the Fermi liquid. All coefficients in Eq. (53) depend on the pressure. Let ${{k}_{x}} \sim {{k}_{y}} \sim \pi {\text{/}}a$ for estimate. Figure 1 shows the theoretical and experimental temperature dependences of the frequency of the second mode at pressures of 7.1, 15.6, and 29.3 bar. For a better presentation, frequencies for 7.1 and 15.6 bar are multiplied by 1.2 and 1.1, respectively. The theoretical dependence is plotted with three fitting parameters T_ca, ${{c}_{{{\text{a}} \bot }}}$, and ${{c}_{{{\text{ul}}}}}$. For all three pressures, the best agreement is reached at ${{c}_{{{\text{a}} \bot }}} \approx 17$ m/s; i.e., this velocity is indeed independent of the pressure and is determined only by the elastic properties of the aerogel. At the same time, the phenomenological coefficient $c_{{{\text{ul}}}}^{2}$ depends on the pressure, but its ratio to $c_{{{\text{l1}}}}^{2}$ hardly depends on the pressure and is approximately equal to 0.01. This result apparently indicates that this ratio depends only on the concentration of impurities.

We now return to the assumption at the beginning of this section that the inequality $\rho _{{\text{a}}}^{{(0)}}\tilde {c}_{{{\text{a5}}}}^{2} \ll {{\omega }^{2}}\frac{{\rho _{l}^{{(0)}}\rho _{{\text{n}}}^{ \bot }}}{{{{{({{\rho }_{{\text{s}}}})}}_{{ij}}}{{k}_{i}}{{k}_{j}}}}$ can be used near T_c. The substitution of the asymptotic expression (51) for the frequency and numerically found parameters gives c_a5 ≪ 150 m/s. The temperature range of applicability for the results is limited by the condition $\rho _{{\text{s}}}^{ \bot }{\text{/}}\rho _{{\text{n}}}^{ \bot } \ll \frac{{c_{{{\text{a}} \bot }}^{2}}}{{c_{{{\text{a5}}}}^{2}}}$. Consequently, for the applicability of the constructed approximation, the anisotropy of velocities in the aerogel should not be too high.

7 CONCLUSIONS

Some conclusions of the work concern the experimental application of the results obtained in it. First, the oscillating modes of ³He and the nematic aerogel found in Section 4 could hardly be excited in oscillating experiments with the aerogel inside superfluid ³He [8] because of the specific boundary conditions in the considered system. The theoretical curve is compared with the experimental dependence in Fig. 1. The longitudinal oscillating modes found in this work for two directions of propagation of vibrations are similar to a slow mode obtained theoretically and detected experimentally in the isotropic silicon aerogel [11]. Therefore, to observe these modes in the system under consideration, it would be reasonable to use the method for excitation of vibrations by means of the transmission of usual sound through the aerogel in different directions. At the same time, the temperature dependence of the frequency of shear oscillations found in this work is in good agreement with the experimental dependence at the fitting elastic coefficients within the estimated range. On one hand, such oscillations can appear because of a very low compressibility of the liquid both outside and inside the system compared to the compressibility of the aerogel. As a result, oscillations occur without a change in the volume of the system. On the other hand, the excitation of such oscillations is a feature of the considered system that is due to the anisotropic properties of the nematic aerogel. The chemical potential of the liquid depends on ${{u}_{{zz}}}$ because of the interaction between ³He and the anisotropic aerogel. The appearance of this dependence is described by the elastic coefficient $c_{{{\text{ul}}}}^{2} \ne 0$ in the expansion of the energy of the system in powers of ${{u}_{{zz}}}$. This coefficient is much smaller than the speed squared of first sound $c_{{{\text{l1}}}}^{2}$ owing to a low concentration of impurities. Oscillations of the normal component of the system can be coupled to oscillations of the superfluid component even at ${{u}_{{ll}}} = 0$ because of the additional term. The beginning of the found temperature dependence of the frequency coincides with the frequency of fourth sound reduced by a factor of ${{c}_{{{\text{a}} \bot }}}{\text{/}}{{c}_{{{\text{ul}}}}}$, and the final section of the dependence coincides with the frequency of shear oscillations of the system with the inclusion of only the normal component of the density. According to the fit of experimental curves, the ratio $c_{{{\text{ul}}}}^{2}{\text{/}}c_{{{\text{l1}}}}^{2}$ is independent of the pressure. Hence, the expression for the frequency of shear oscillations could be used to analyze the temperature dependence of the superfluid density and the degree of its anisotropy in the temperature range where the condition $\rho _{{\text{s}}}^{ \bot }{\text{/}}\rho _{{\text{n}}}^{ \bot } \ll \frac{{c_{ \bot }^{2}}}{{c_{{{\text{a5}}}}^{2}}}$ is valid. The elastic characteristics of nematic aerogels have not yet been systematically measured. For the correct interpretation of the results obtained from comparison with experimental data, the condition $\frac{{c_{ \bot }^{2}}}{{c_{{{\text{a5}}}}^{2}}}$ < 0.1 should be satisfied (since $\rho _{{\text{s}}}^{ \bot }{\text{/}}\rho _{l}^{{(0)}} \sim 0.1[1 - T{\text{/}}{{T}_{{{\text{ca}}}}}]$ follows from Eq. (53)). The system of impurities consisting of strands that are ideally codirected and specularly reflect quasiparticles satisfies the Anderson theorem; i.e., such impurities do not change the superfluid properties of the polar phase such as the superfluid transition temperature and the temperature dependence of the band gap in the spectrum of excitations [14]. Consequently, the measurement of the temperature dependence of the superfluid density allows one to estimate the degree of satisfaction of this theorem for real aerogels. It is noteworthy that the contribution of impurities to the superfluid density in the considered system is due not only to the scattering of quasiparticles on strands but also to the added mass effect, which appears in the potential flow around strands in the direction perpendicular to them. This contribution cannot be calculated in the hydrodynamic approximation used in this work, but it is undoubtedly finite. Therefore, this effect should be excluded to verify the satisfaction of the Anderson theorem.