Artificial materials and systems similar to natural graphene with a Dirac cone in the dispersion relation but in a different range of the parameters are currently fabricated and studied [1–4]. Hexagonal lattices of antidots with a period of 80–120 nm, which are formed nanolithographically in a high-mobility two-dimensional electron gas of GaAs/AlGaAs heterostructures, are called semiconductor artificial graphene [4, 5]. Semiconductor artificial graphene has two interesting Dirac points: the first point appears at the crossing of the two lowest minibands, and the second occurs at the intersection of the fourth and fifth minibands [6–9]. It was shown that Landau–Dirac quantization in the absence of disorder occurs near a Dirac point in very weak magnetic fields B < 10 mT [5]. However, Dirac points in quantum transport in semiconductor artificial graphene have not yet been detected. The main reason is disorder [9, 10], and the existence of Dirac points in semiconductor artificial graphene is currently indicated only by the study of photoluminescence at interband transitions in a GaAs quantum well at B = 0 [4]. Nevertheless, manifestations of the magneto-electric miniband spectrum of the lattice or the Hofstadter butterfly [11] were detected on a square lattice with a period of about 100 nm, when the Fermi energy EF was much higher than the modulation amplitude V [12]. A nonmonotonic behavior of the Hall resistance was observed for high Landau levels; disorder was well screened in this case.

The height of potential barriers at antidots should be much higher than the Fermi level for a pronounced Dirac cone to appear in semiconductor artificial graphene. The effect of disorder in this case becomes strong and can destroys the Dirac point [9]. Measurements show that observed effects depend on the amplitude of periodic modulation [13]. In particular, only effects of magnetic breakdown are observed at weak modulation [14, 15], and they disappear with increasing modulation amplitude. According to the calculation of quantum transport in semiconductor artificial graphene disregarding disorder, plateaus of the hole and electron conductivities are formed below and above the zeroth Landau level in the electron density at low magnetic fields [5]. Magneto-electrical minibands and edge states in semiconductor artificial graphene at high magnetic fields have recently been simulated disregarding disorder [16]. The integral effect of the lattice can be revealed from DoS(n, B) maps of the density of states, i.e., Wannier diagrams, where n is the charge carrier density and B is the magnetic field [17]. In particular, this concerns the experimentally studied graphene superlattices, which have a period of about 15 and 35 nm and demonstrate the cloning of the main Dirac point and Hofstadter butterfly [1–3].

In this work, we present Wannier diagrams calculated for various modulation amplitudes of the semiconductor lattice of antidots taking into account short-range disorder. The calculations of the Hall resistance Rxy show a close relation between DoS(n, B) and Rxy(n, B) maps. Calculated maps of the density of states can allow one to forecast the measurement results and to estimate real modulation and disorder levels.

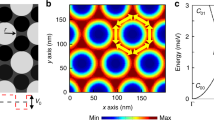
The calculations were performed with the analytically specified potential U(r) = Vd(r) + V0Σcos(gi · r) of the hexagonal lattice with the period L on a 2–3 μm square, where V0 is the amplitude of potential mo-dulation, the function Vd(r) = Vrδ with a random number δ ranging from –0.5 to 0.5 and the disorder amplitude Vr specifies a random addition to the potential of the lattice in each cell of the discrete lattice (hx = hy = 8 nm) [15], and gi, i = 1–3, are the reciprocal lattice vectors given by the expressions

$${\mathbf{g}_{1}} = {{g}_{0}}(1,1{\text{/}}\sqrt 3 ),$$
(1)
$${\mathbf{g}_{2}} = {{g}_{0}}(0,2{\text{/}}\sqrt 3 ),$$
(2)
$${\mathbf{g}_{3}} = {\mathbf{g}_{1}} - {\mathbf{g}_{2}} = {{g}_{0}}(1, - 1{\text{/}}\sqrt 3 ),$$
(3)

where g0 = 2π/L. It was shown in [9] that the band structure of the lattice depends only on the dimensionless amplitude of potential modulation w0 = 0.5V0/E0, where \({{E}_{0}} = \frac{{8{{\pi }^{2}}}}{9}\frac{{{{\hbar }^{2}}}}{{m{\text{*}}{{L}^{2}}}}\) is the characteristic energy, which is equal to 1.56 meV for the effective mass of the electron in GaAs \(m\text{*} = 0.067{{m}_{e}}\) and the lattice period L = 80 nm. At low modulation w0 < 1, the third and higher minibands of the lattice are imposed on the second miniband. As modulation increases, minibands rise and are flattened, so that the third flat band and the second Dirac point are already formed at w0 = 1.5 [9].

Lattices are described in terms of the characteristic carrier density \({{n}_{0}} = 2{\text{/}}(\sqrt 3 {{L}^{2}}{\text{/}}2)\) corresponding to two particles per cell and the characteristic magnetic field B0 at which the magnetic flux \(\phi = B\sqrt 3 {{L}^{2}}{\text{/}}2\) through the cell of the lattice is \({{\phi }_{0}} = h{\text{/}}e\). It is noteworthy that n0 = n1D, where n1D is the carrier density at the first Dirac point. For the lattice period L = 80 nm, B0 ≈ 0.75 T and n0 ≈ 3.6 × 1010 cm–2.

The potential on the strip beyond the square region under consideration was assumed uniform and equal to the minimum potential of the lattice in the absence of disorder. Then, the problem of two-dimensional single-particle quantum scattering of electron waves incident on the mentioned square from the left and right was solved by the recursive Green’s functions method [18]. As a result, we obtained the local density of states as a function of the energy E and the magnitude B of the perpendicular magnetic field. The integration of DoS(E) over a wide energy range up to EF gives n(EF) at a given B value [19]. It was shown that the introduction of a small imaginary part of the energy in the definition of the Green’s function makes it possible to effectively smooth interference oscillations in DoS(E) without loss of the accuracy of calculation of the carrier density. The magnetic field B was additionally varied with a small step from 0 to 2 T corresponding to the quantum Hall effect. These calculations were carried out with the lattice period L = 80 nm; the local disorder amplitude Vr = 2 meV for the modulation amplitudes w0 = 0.1, 0.25, 0.5, and 1; and the local disorder amplitude Vr = 5 meV for the modulation amplitude w0 = 1.5. As a result, we obtained DoS(E, B), DoS(n, B), and EF(n, B) maps.

Figures 1 and 2 show the corresponding maps, where the yellow and blue regions correspond to the maximum and minimum densities of states. These maps demonstrate transition from the fan of Landau levels (at w0 = 0.1) to an almost periodic pattern (at w0 = 1) in the region of low carrier densities (\(n < 2{{n}_{0}}\)) and low magnetic fields (\(B < 2{{B}_{0}}\)). In the calculations, the total modulation amplitude varied from 1.4 meV (at w0 = 0.1) to 21.1 meV (at w0 = 1.5) and the cyclotron energy ℏωc varied from 0 to 3.46 meV at 2 T.

Fig. 1.
figure 1

(Color online) DoS(n, B) maps for the lattice with the modulation amplitudes w0 = 0.1 and 0.25.

Full size image
Fig. 2.
figure 2

(Color online) DoS(n, B) maps for the lattice with the modulation amplitudes w0 = 0.5 and 1.

Full size image

Modulation in the first two maps is comparatively weak and Landau levels (Shubnikov–de Haas oscillations) are manifested as maxima of the density of states. Dips in the density of states between them diverge as rays from the point n = B = 0 and correspond either to edge states (inclined lines), when electrons are absent inside the lattice and move only along the edge of the lattice, or to band gaps in the lattice (horizontal lines), when electrons do not enter the sample at all. The slope \(k = \tilde {n}{\text{/}}\tilde {B}\) of dark lines in the dimensionless variables \(\tilde {n} = n{\text{/}}{{n}_{0}}\) and \(\widetilde B = B{\text{/}}{{B}_{0}}\) is directly related to the quantized conductance \(G = k{{G}_{0}}\), where G0 = 2e2/h, or the quantized Hall resistance Rxy = R0/k, where R0 = 1/G0: dark lines determine the centers of quantized conductance or resistance plateaus. According to our calculations, the Rxy plateaus are always wider than dips in the density of states. Fans of rays on the (n, B) map of the density of states correspond to the formation of Landau levels from the miniband edges and originate from the (ln0, mB0) points, where l and m are integers.

An upward ray with a slope of k = 1 and a much less pronounced downward ray with a slope of k = –1 ori-ginate from the (n0, 0) Dirac point at w0 = 0.1. The (2n0, B0) and (3n0, B0) points are the centers of rays with different slopes; a ray with a slope of +1 originates from the (0, B0) point. Lines parallel to the main rays separating Landau levels appear. For example, a ray with a slope of k = 2, which enters the (3n0, B0) point from above, can be continued down to the first Dirac point. The map of rays becomes more pronounced at w0 = 0.25 and 0.5. Since rays correspond to the centers of the Hall resistance plateaus, the quantum Hall picture should be very unconventional and should contain three of four replicas of the first Rxy = R0 plateau. Although the dispersion relation for w0 = 0.1–0.5 at B = 0 is gapless, a horizontal ray originating from the (2n0, B0) point at w0 = 0.1–0.25 continues toward low and high magnetic fields at w0 = 0.5. The band gap can be washed out by disorder, but it is manifested in the calculations as a region of high resistances.

The band gap between the second and third minibands already exists at w0 = 1 and is manifested as a horizontal ray originating from the (2n0, 0) point on the map of the density of states. The map for carrier densities below 2n0 is almost periodic in magnetic field with a period of B0. Two rays with slopes of +1 and ‒1, as well as downward rays with slopes of –3, –5, and ‒7, which indicate Landau–Dirac quantization, originate from the second Dirac point (4n0, 0). At higher carrier densities, the clear pattern disappears because of the overlapping of different minibands of the lattice. The third (flat) miniband of the lattice has a high density of states and is manifested in the bright strip of the density of states beginning at the (E = 2 meV, B = 0) point in Fig. 3. The DoS(E, B) map is similar to the Hofstadter butterfly, which was calculated in almost three B0 periods for a finite lattice with a total modulation of 14 meV taking into account disorder. When the energy is recalculated to the corresponding carrier density, regions with a low density of states are contracted to narrow strips, whereas regions with a high density of states are expanded; as a result, the entire curved DoS(E, B) map is straightened out to a series of rays on the (n, B) plane (analog of the Wannier diagram).

Fig. 3.
figure 3

(Color online) DoS(E, B) map for the modulation amplitude w0 = 1.

Full size image

An additional horizontal line at a carrier density of n = 6n0 = 21.65 × 1010 cm–2 appears in Fig. 4 at w0 = 1.5 after filling of six minibands in the magnetic field. Strong disorder with the amplitude Vr = 5 meV washes out the fine structure of the density of states. Rays with slopes of +1 and –1 dominate, whereas the fan of conventional Landau levels disappears. The right panel of Fig. 4 shows the EF(n, B) map, where color varies from dark blue corresponding to –4 meV to yellow for 8 meV. The function EF(n = const, B) is an almost periodically oscillating function.

Fig. 4.
figure 4

(Color online) (Left) DoS(n, B) and (right) EF(n, B) maps for the modulation amplitude w0 = 1.5 at Vr = 5 meV.

Full size image

Hall resistances were calculated using the Kwant software package [20] with the potential and disorder defined with the same formulas as before. The calculation was performed in the four-terminal configuration: two horizontal channels through which electron scattering occurs are connected to the left side of the square with the lattice, at top and bottom, and to the right side of it. Four-terminal resistances were reconstructed by Büttiker formulas [21] from the calculated transmission coefficients between terminals in the sy-stem.

Figure 5 shows the magnetic field dependence of the Hall resistance calculated at a carrier density of n = 6 × 1010 cm–2, a disorder amplitude of Vr = 2 meV, and three modulation amplitudes. As the magnetic field increases, the Hall resistance Rxy(B) successively intersects strips of dips of the density of states with slopes of +1 and –1, demonstrating a sawtooth behavior. The R0/2 and R0/3 plateaus are not seen because they are narrow. The ranges of a negative Hall resistance indicate a hole conductivity. The behavior of Rxy(B) correlates with DoS(n, B) maps and becomes more pronounced with increasing modulation amplitude. The Rxy(B) curve at w0 = 1.5 passes through zero almost exactly at jB0/2, where j = 1–5. In addition, it is remarkable that even strong short-range disorder taken into account in our calculations does not destroy quantized Hall resistance plateaus. Long-range disorder, which is due to slightly different sizes of holes in the gate specifying the lattice of antidots, provides a much stronger effect. Our calculations show that this disorder destroys the quantization of the Hall resistance at low magnetic fields B < B0/2 (Rxy values decrease, but the sign holds) and suppresses lattice effects in high magnetic fields B0 < B < 3B0.

Fig. 5.
figure 5

(Color online) Magnetic field dependence of the Hall resistance Rxy(B) calculated for w0 = 0.25, 0.5, and 1.5 at a carrier density of n = 6 × 1010 cm–2 and Vr = 2 meV.

Full size image

To summarize, the DoS(E, B), DoS(n, B), and EF(n, B) maps of semiconductor artificial graphene have been calculated for potential modulation amplitudes comparable to or much larger than the Fermi energy. These maps illustratively and deeply represent the Landau–Dirac quantization, Hofstadter butterfly, and magneto-electric oscillations of the Fermi level. It has been shown that the fan of Landau levels on the (n, B) maps is transformed with increasing lattice modulation to a rhombic structure formed by a set of parallel rays with different slopes of opposite signs. The feature of semiconductor artificial graphene is the alternation of hole and electron charge carriers; as a result, the Hall resistance Rxy(B) oscillates between negative and positive values. The simulation results can contribute to the interpretation of measurements of the magnetotransport in lattices, e.g., Wannier diagrams, which were obtained by capacitive measurements of the density of states in short-period graphene superlattices [2, 3].