Theoretical Modeling of High Spin to Low Spin Transition and Structural Stability Under Pressure in CaFeO₃

Evolution of magnetic and spectral properties and structure stability of CaFeO₃ are investigated in frames of the GGA + U method. It is shown that the GGA + U method is able to reproduce the transition from high spin to low spin under pressure obtained experimentally. At ambient pressure monoclinic structure has lower energy which agrees with experiment. Full structural relaxation shows that orthorhombic structure in unstable above 30 GPa and undergoes a distortion toward monoclinic structure.

1 INTRODUCTION

Compounds with a perovskite structure have been intensively investigated during the last decades due to the variety of electronic and magnetic properties and the high interest for practical applications [1–7]. The metal–insulator transition observed in transition metal oxides such as perovskites is also of interest from both a theoretical point of view and a practical application [8–12]. The series of perovskite compounds ABX₃ has a 3D structure made of BX₆ octahedra with large A cations placed in spaces between them, where B is usually a transition metal and X is an element of the VI group of the periodic table. Charge, orbital, or magnetic ordering is observed in many compounds with perovskite structure [13]. On its turn, CaFeO₃ is of interest due to unusual valence of iron ions Fe⁴⁺ which is in a high spin (HS) state at ambient pressure and has an electronic configuration ${\text{t}}_{{2g}}^{3}$${\text{e}}_{g}^{1}$. Since the two times degenerate ${{e}_{g}}$ subshell is occupied by one electron, the instability known as the Jahn–Teller effect could arise. It is energetically favorable to lift the degeneracy by distorting the octahedron around the transition metal. Another way for lifting the degeneracy and minimizing the total energy is charge ordering or charge disproportionation (CD) which is observed in CaFeO₃ in low temperature phase.

CaFeO₃ has a perovskite-like structure consisting of corners-shared octahedra FeO₆ and Ca ions in the spaces of this 3D structure. Unlike the cubic perovskite CaTiO₃, the structure of CaFeO₃ is distorted by the tilt of the octahedra, leading to orthorhombic or monoclinic symmetry. Takeda et al. showed that at room temperature CaFeO₃ has $Pnma$ space group with unit cell parameters $a = 5.34967(9)$ Å, b = $7.53558(14)$ Å, $c = 5.32356(10)$ Å [4] and the average Fe–O bond length is 1.91870(6) Å. With decreasing temperature a CD state occurs at ${{T}_{{{\text{CD}}}}} \approx 290$ K, that leads to phase transition to the monoclinic structure with $P{{2}_{1}}{\text{/}}n$ space group and parameters of the unit cell a = 5.31382(3) Å, b = 5.34775(4) Å, c = 7.52058(5) Å, and two inequivalent FeO₆ octahedra [1]. The average Fe–O bond length for the small octahedron is 1.87244(6) Å, and for the larger one is 1.97317(6) Å.

Charge disproportionation in CaFeO₃ at ambient pressure was investigated previously in frames of LDA + U method using Coulomb parameter values $U = 5.4$ eV and $J = 0.95$ eV [5]. The authors showed that the total number of electrons is ≈5.1 for both types of iron which corresponds to electronic configuration Fe-$3{{d}^{5}}$. The authors propose that CD can be described as: $2{{d}^{5}}\underline L ({\text{F}}{{{\text{e}}}^{{4 + }}}) = {{d}^{5}}{{\underline L }^{2}}({\text{F}}{{{\text{e}}}^{{5 + }}}) + {{d}^{5}}({\text{F}}{{{\text{e}}}^{{3 + }}})$, where $\underline L$ is hole in oxygen $2p$ band.

At ambient pressure and temperature above 290 K CaFeO₃ is paramagnetic without CD and all iron ions are equivalent and have Fe⁴⁺ valence. With decreasing temperature, the CD state with Fe³⁺ and Fe⁵⁺ ions is observed below 290 K, but CaFeO₃ remains paramagnetic until the CD AFM phase occurs at ${{T}_{N}} = 115$ K. In the pressure range 0–17 GPa, the CD temperature is T_CD = 290 K. At a pressure above 20 GPa, T_CD decreases to 6 K and ${{T}_{N}}$ increases under pressure from 125 to 400 K.

2 METHOD

The GGA + U calculations and full crystal structure relaxation were performed using the pseudopotential method implemented in the Quantum ESPRESSO package [14]. We use the exchange-correlation potential in the form proposed by Perdew, Burke, and Ernzerhof [15]. A similar approach was previously successfully applied to model the structural transition and describe the evolution of magnetic properties in correlated materials under pressure [16]. Pseudopotentials were taken from the Materials Cloud library [17, 18] and the kinetic energy cutoff ${{E}_{{{\text{cut}}}}} =$ 90 Ry was used. To take into account the correlation effects, $U = 4.5$ eV and $J = 0.95$ eV were applied to the Fe d‑shell. This set of Coulomb repulsion parameters allows one to reproduce the critical pressure of spin transition in good agreement with the experiment.

3 RESULT AND DISCUSSION

In order to take into account the effects of strong electron correlation in CaFeO₃, we applied the GGA + U method for calculating the evolution of its magnetic and structure properties under pressure. According to experimental data, CaFeO₃ has a $Pnma$ structure and is paramagnetic without CD above 290 K. In the monoclinic phase and below 125 K, CaFeO₃ becomes A-type AFM [6]. However, the DFT + U method requires setting some magnetic long-range order and cannot be used for description of paramagnetic systems with local magnetic moments. In order to treat CaFeO₃ above ${{T}_{N}}$ we consider three magnetic orders, namely AFM-A, AFM-C, and AFM-G for both structures: $Pnma$ and $P{{2}_{1}}{\text{/}}n$. For each magnetic order full structure optimization. The total energies obtained in the calculation are shown in Table 1. One can see that the AFM-A ordering has the lowest total energy for both structures that agrees with experimental data for monoclinic structure. One can see that the AFM-A ordering persists through the structural transition and its traces could be observed in the $Pnma$ structure at high pressure.

Table 1. Total energies of CaFeO₃ (eV) for different types of magnetic order obtained in GGA + U for $U = 4.5$ eV and $J = 0.95$ eV. The energy of AFM-A was set as zero for each structure

Optimization of the crystal structures in the framework of the GGA + U method shows that both structures are stable at ambient pressure. The volume of FeO₆ octahedra remains equal in $Pnma$ phase. The difference between them in the $P{{2}_{1}}{\text{/}}n$ structure is $\Delta V = 1.5$ ų. The length of the Fe–O bond obtained in GGA + $U$ is shown in Table 2 and agrees well with the experimental data [1]. The monoclinic structure $P{{2}_{1}}{\text{/}}n$ has the total energy 0.029 eV lower than the orthorhombic $Pnma$ structure in agreement with the experimental phase diagram showing that the $Pnma$ phase is stable only above 290 K. Note, that the GGA + U method describes the ground state and all obtained values correspond to $T = 0$ K. One can see that GGA + U provides a good description of the structure and magnetic properties of CaFeO₃ at ambient pressure and can be applied to investigate its properties under pressure.

Table 2. Fe–O bond length in CaFeO₃ (Å) as obtained in GGA + U for $U = 4.5$ eV and $J = 0.95$ eV for $Pnma$ and $P{{2}_{1}}{\text{/}}n$ structures. Experimental data are taken from [1]

Often, the CD state is accompanied by a metal-insulator transition. Density of states (DOS) obtained in the spin-polarized GGA + U calculation is pr-esented in Fig. 1. Strong hybridization of Fe-d and O-p states leads to a wide $p{\kern 1pt} - {\kern 1pt} d$ band lying in the range from –8 to 4 eV. One can see that CaFeO₃ in orthorhombic $Pnma$ structure exhibits metal behavior (Fig. 1a). The monoclinic phase has two types of Fe atoms placed in the center of large and small octahedra denoted Fe_L and Fe_S, respectively (see Figs. 1b and 1c). The splitting between the Fe-d bands can be explained by the fact that the hybridization between Fe and O is stronger in the small octahedron (Fe–O bond length 1.8744 Å) than in the large one (Fe–O bond length 1.9760 Å). DOS for the monoclinic structure has a pseudogap and therefore the CaFeO₃ in $P{{2}_{1}}{\text{/}}n$ phase should be a bad metal at finite temperature, in agreement with experimental data [1].

Fig. 1.

(Color online) DOS of CaFeO₃ obtained in GGA + U for 0 GPa. Upper panel $Pnma$ phase, middle panel $P{{2}_{1}}{\text{/}}n$ phase, lower panel partial Fe d-shell DOS for $P{{2}_{1}}{\text{/}}n$ structure, subscript L denoted Fe in large octahedron and S for iron in small octahedron. Coulomb parameters are $U = 4.5$ eV and $J = 0.95$. Fermi level was set to 0 eV.

As the next step, a series of calculations was performed for different external pressures (cell volumes). For each pressure, full relaxation of the crystal structure was performed. The unit cell parameters obtained in the GGA + U calculation are in a good agreement with the experimental data [1].

If the shape of the unit cell was not preserved during relaxation of the crystal structure, the orthorhombic phase keeps the symmetry below 30 GPa only. At higher pressures FeO₆ octahedra become non-equivalent indicating that the monoclinic structure might be favorable. The length of Fe–O bonds at different pressures obtained in GGA + U is shown in Fig. 2. One can see that the bond length is tending to the values obtained for monoclinic phase. Note, that the relaxed orthorhombic structure differs from the relaxed monoclinic structure, which gives two metastable structures with non-equivalent octahedra. However, the high pressure XRD shows that orthorhombic structure is stable above 30 GPa at room temperature [2]. The two explanations for this result are as follows: first, the Quantum Espresso package implies the Dudarev simplified version of DFT + U for a full relaxation regime [19] and orbital polarization is not strong enough to accomplish this transition; second, this transition is entropy driven and proper accounting of phonon entropy and temperature is necessary. Similar results were obtained for transition under pressure in FeS [20]. It was shown recently, that transition from $P{{2}_{1}}{\text{/}}n$ to $Pnma$ structure under pressure could be reproduced in the framework of DFT + DMFT method [21] at finite temperature without full relaxation of atomic positions but with accurate accounting for many body correlation effects, which underscores the importance of the temperature effects.

Fig. 2.

(Color online) Pressure dependence of the Fe–O bond length for (red diamonds) orthorhombic structure with equivalent octahedron, (green and red triangles for large and small octahedra, respectively) distorted orthorhombic structure, and (black circles and blue squares for large and small octahedra, respectively) monoclinic structures obtained in GGA + U calculations.

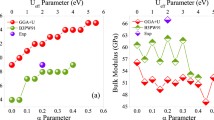
The Coulomb repulsion value $U = 4.5$ eV and the Hund’s parameter value $J = 0.95$ eV used in the calculation provide spin transition pressure ≈35 GPa, which is close to the experimental value 30 GPa at room temperature. The magnetic moment values for both structures are shown in Fig. 3. At pressures lower than 30 GPa, the LS solution was unstable and only HS was obtained. In the pressure range 30–40 GPa the magnetic moment decreases from 3.18${{\mu }_{B}}$ to 1.6${{\mu }_{B}}$ which indicates the spin transition. This agrees well with the experimentally observed HS state in CaFeO₃ at ambient pressure [2]. Calculations made for $P{{2}_{1}}{\text{/}}n$ show similar magnetic collapse with decreasing of magnetic moments from 3.55${{\mu }_{B}}$ for Fe(1) and 2.7${{\mu }_{B}}$ for Fe(2) to 1.52${{\mu }_{B}}$ and 1.47${{\mu }_{B}}$, respectively (see Fig. 3).

Fig. 3.

(Color online) Magnetic moment obtained in GGA + U for (red) $Pnma$ and (black and blue) $P{{2}_{1}}{\text{/}}n$ structures.

4 CONCLUSIONS

In the present work, magnetic and spectral properties of CaFeO₃ $Pnma$ and $P{{2}_{1}}{\text{/}}n$ phases under pressure have been investigated in the framework of the GGA + U method. A-type AFM was found energetically favorable for both structures that agrees with experimental data for monoclinic phase below 115 K [22].

With increasing pressure and decreasing Fe–O distance, hybridization increases, leading to the HS-to-LS transition at ≈35 GPa and magnetic moment decreases from 3.18${{\mu }_{B}}$ to 1.6${{\mu }_{B}}$ in orthorhombic structure and from 3.55${{\mu }_{B}}$ for Fe(1) and 2.7${{\mu }_{B}}$ for Fe(2) to 1.52${{\mu }_{B}}$ and 1.47${{\mu }_{B}}$, respectively, in monoclinic phase.

It was shown that GGA + U can describe metal–insulator transition at ambient pressure and HS to LS transition under pressure in both phases of CaFeO₃. However, the structural phase transition cannot be reproduced in the framework of the GGA + U method. The explanation of this could be the following: the transition occurs in the paramagnetic phase and GGA + U requires setting a long range magnetic order. Another explanation is that the ground state is calculated in the framework of DFT + U, which assumes $T = 0$ K, whereas the impact of temperature and vibrational entropy [20] could be important for a proper description of the phase transition under pressure in CaFeO₃.