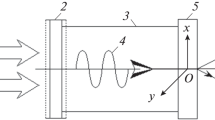
It is shown that a nanosecond unipolar soliton-like pulse of the type of a localized shear deformation autowave propagating perpendicular to the magnetic field can be formed in a cubic paramagnetic crystal subjected to longitudinal static deformation in the direction of external magnetic field. The influx of the energy stored in paramagnetic ions into the pulse due to the nonequilibrium initial population of their stationary quantum states is compensated by irreversible losses caused by pulse damping due to its interaction with thermal lattice vibrations, defects, and microinhomogeneities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 INTRODUCTION
One of the trends in the development of physical acoustics is the search and prediction of phenomena similar to those found or predicted in nonlinear optics [1]. This concerns to a great extent the nonlinear phenomena related to the soliton dynamics. In particular, after the discovery and theoretical explanation of the resonant optical effect of self-induced transparency (SIT) [2], acoustic SIT (ASIT) on paramagnetic impurities in solids was revealed and theoretically investigated in detail [3–5]. Acoustic analogues of nonresonant optical solitons have also been actively studied [6].
The durations of the investigated acoustic solitons vary in a wide range: from micro- to subpicoseconds [7, 8]. The carrier frequencies lie in the far ultrasonic range: from units to hundreds of gigahertz.
The aforementioned trend is also observed when studying optical and acoustic solitons of increasingly shorter durations, containing about one or even half of the period of oscillations of the corresponding physical nature [9–17]. To date, one can speak with confidence about optical and acoustic unipolar (half-period) pulses [15, 16].
We should highlight separately the investigations of dissipative optical solitons [18–24]. The properties of both quasi-monochromatic and unipolar solitons have been studied. In agreement with the above-mentioned trend, acoustic analogues of optical dissipative solitons were considered [25, 26].
Note that the soliton-like solutions investigated in [25, 26] and [27–29] cannot be considered as dissipative in the rigorous sense. The point is that, in contrast to dissipative solitons (described, e.g., in monograph [18]), these soliton-like solutions can be implemented for a short time, limited by the characteristic relaxation time \({{T}_{1}}\) of quantum level populations. Therefore, these solutions were referred to as soliton-like dissipative structures (objects) [25, 26], which have analogues in optics [27–29]. Thus, the longer \({{T}_{1}}\), the longer the lifetime of these soliton-like objects is.
It was proposed in [30] to use excited Raman sublevels as long-lived quantum states. The direct quantum transition between Raman sublevels is forbidden. This transition may occur only via an intermediate quantum level of higher energy. Thus, the allowed transition has a two-photon nature. Under these conditions unipolar soliton-like objects can be formed at inverse population of Raman sublevels [30]. The amplification of these objects due to the influx of the energy stored on Raman sublevels is compensated by losses caused by irreversible relaxation in the system of other quantum transitions.
In this paper, we report the results of studying the fundamental possibility and conditions for the formation of unipolar localized objects of acoustic nature due to two-phonon transitions in a system of non-equilibrium populated Stark and Zeeman sublevels of paramagnetic impurity ions.
2 STATEMENT OF THE PROBLEM AND BASIC EQUATIONS
Let a cubic crystal containing paramagnetic impurity ions be placed in an external magnetic field B and a longitudinal static strain field. Both fields are directed along the z axis, parallel to the fourfold crystallographic axis. The static deformation forms the gradient of the intracrystalline electric field, causing a quadrupole Stark splitting of the quantum levels of paramagnetic ions. In turn, the magnetic field causes Zeeman splitting of these levels. In the perpendicular direction, along the x axis, a unipolar transverse ultrasonic pulse (shear strain pulse) is applied to the crystal. This pulse forms local gradients of internal electric field in the crystal, which cause (due to the van Vleck mechanism [31, 32]) quadrupole quantum transitions between the paramagnetic ion sublevels formed in the aforementioned static fields.
It has been shown experimentally that the paramagnetic ions with effective spin \(S = 1\) interact most strongly with the lattice strain field [32]. The magnetic field removes the degeneracy in the projection \({{S}_{z}}\) of this spin on the z axis. Due to the quadrupole Stark effect in the static strain field the degeneracy in the modulus of the projection \({{S}_{z}}\) of this spin on the z axis is removed. As a result, a nonequidistant three-level system (see Fig. 1) is formed in the paramagnetic ion. It is assumed that Stark splitting dominates over Zeeman splitting.
Splitting of the quantum state of effective spin in a strong field of longitudinal static strain \(\varepsilon _{{zz}}^{{(0)}}\) and a weak magnetic field parallel to the strain field. The magnetic field, directed along the z axis, removes the degeneracy in the effective-spin projection on this direction, while the static strain field removes the degeneracy in the modulus of this projection.
The Hamiltonian of the effective spin, interacting with the aforementioned static fields and the local shear strain field of the ultrasonic pulse, has the form [32]
Here, ℏ is the reduced Planck constant; ω0 = gμBB/ℏ is the frequency of Zeeman splittings of spin sublevels; μB is the Bohr magneton; g is the Lande factor; \({{G}_{\parallel }}\) and \({{G}_{ \bot }}\) are the constants of interaction of longitudinal and transverse crystal deformations with the effective spin, respectively; \({{\varepsilon }_{{zx}}} = 0.5\partial {{u}_{z}}{\text{/}}\partial x\) is the shear strain tensor component of the crystal; \({{u}_{z}}\) is the component of the shear vector of the unipolar pulse applied to the crystal; and \({{\hat {S}}_{z}}\) and \({{\hat {S}}_{x}}\) are the spin matrices, which can be written as [32]
Representing the density matrix \(\hat {\rho }\) of the effective spin in the form
and using the von Neumann equation with allowance for Eqs. (1) and (2), we arrive at
Here,
the subscripts +, 0, and – of density matrix elements denote the effective spin projections \({{S}_{z}}\) equal to +1, 0, and –1, respectively (Fig. 1); \({{\omega }_{ + }} = {{\omega }_{S}} + {{\omega }_{0}}\) and \({{\omega }_{ - }} = {{\omega }_{S}} - {{\omega }_{0}}\) are the frequencies of the quantum transitions \( + \leftrightarrow 0\) and \( - \leftrightarrow 0\), respectively; and \({{\omega }_{S}} = {\text{|}}{{G}_{\parallel }}\varepsilon _{{zz}}^{{(0)}}{\text{|/}}\hbar \) is the frequency of quadrupole Stark splitting due to the static deformation of the crystal.
The quantum state populations satisfy the normalization condition \({{\rho }_{{ + + }}} + {{\rho }_{{00}}} + {{\rho }_{{ - - }}} = 1\).
The relaxation terms were neglected in material equations (4)–(7), because the pulse duration τp is assumed to be much shorter than all relaxation times. This condition is satisfied with good margin for nanosecond pulses, because the characteristic phase relaxation time \({{T}_{2}}\) and the relaxation time of quantum level populations, \({{T}_{1}}\), are on the order of 10–5 and 10–3 s, respectively [3].
Here, the validity of the inequality \({{G}_{\parallel }}\varepsilon _{{zz}}^{{(0)}} < 0\) is of importance. Specifically in this case, the energy of the state with \({{S}_{z}} = \pm 1\) is lower than that of the state with \({{S}_{z}} = 0\) (Fig. 1). For example, for Fe2+ ions incorporated into a cubic MgO crystal, \({{G}_{\parallel }} > 0\) [3]. Hence, \(\varepsilon _{{zz}}^{{(0)}} < 0\) in this case. Thus, the static deformation must be of compression type.
The condition of dominance of quadrupole Stark splitting over Zeeman splitting has the form of inequality \({{\omega }_{S}} \gg {{\omega }_{0}}\). Having taken the values \({{G}_{\parallel }} \sim {{10}^{{ - 13}}}{\kern 1pt} \) erg [3, 31] and \({\text{|}}\varepsilon _{{zz}}^{{(0)}}{\text{|}} \sim {{10}^{{ - 4}}}\) for the example considered above, we obtain \({{\omega }_{S}} \sim {{10}^{{10}}}\) s–1. The magnetic field magnitude \(B\) can be chosen so as to make the Zeeman splitting frequency \({{\omega }_{0}}\) be on the order of 108 s–1. Under these conditions the inhomogeneous broadening \(\delta \omega \) of involved quantum transitions, for which \(\delta \omega \sim {{10}^{7}}\) s–1, can be neglected [33].
Using the semiclassical approach, we will write the one-dimensional equations for the shear strain field [13] as
where
\({{p}_{z}}\) is the volume density of local shear strain pulse along the z axis; ρ and a are the equilibrium density of crystal and the linear velocity of transverse sound in it, respectively. Integration is performed over the entire crystal volume.
Hence, using Eqs. (1)–(3) and (8), we arrive at
where n is the concentration of paramagnetic ions.
The left-hand side of (9) contains an additional (last) empirical term, which describes the damping of ultrasound during its interaction with thermal lattice vibrations, defects, microinhomogeneities, etc. [37, 38]; q is the damping parameter.
Thus, the self-consistent system of Eqs. (4)–(7) and (9) describes the nonlinear propagation of transverse ultrasound in a magnetized and statically deformed paramagnetic crystal.
The ultrasound damping, described by the last term on the left-hand side, can be compensated by the energy stored at nonequilibrium population of Zeeman states of paramagnetic ions. For example (as will be assumed below), the state with \({{S}_{z}} = + 1\) may be initially more populated than the state with \({{S}_{z}} = - 1\) (Fig. 1).
The above estimates demonstrate fulfillment of the condition
which can be used to simplify material equations (4)–(7). Then, the left-hand sides of Eq. (4) can be approximated to \(\partial {{\rho }_{{ + 0}}}{\text{/}}\partial t = \partial {{\rho }_{{0 - }}}{\text{/}}\partial t\) = 0. Then, expressing \({{\rho }_{{ + 0}}}\) and \({{\rho }_{{0 - }}}\) from (4) and substituting the obtained expressions into (5) and (6), with allowance for the inequality \({{\omega }_{S}} \gg {{\omega }_{0}}\), we arrive at the system
where \(Q = {{\Omega }^{2}}{\text{/}}{{\omega }_{S}}\) and the real Bloch variables
are introduced.
Performing similar transformations on the right-hand side of (9), we obtain
where \(a_{0}^{2} = {{a}^{2}}[1 - \eta (1 - 3{{w}_{0}})]\), \(\eta = \frac{{nG_{ \bot }^{2}}}{{16\hbar {{\omega }_{S}}\rho {{a}^{2}}}}\), and \({{w}_{0}}\) is the initial population of the upper quantum state with \({{S}_{z}} = 0\).
When deriving (12), we used the normalization condition for quantum level populations, with \({{\rho }_{{00}}} \approx {{w}_{0}}\) because of condition (10).
The system of material equations (11) is analogous to the system describing the two-photon transitions between Raman sublevels in the case of stimulated Raman scattering [36]. The Zeeman sublevels, characterized by the effective spin projections \({{S}_{z}} = \pm 1\), and the frequency \(2{{\omega }_{0}}\) of the transition between these sublevels serve as the Raman sublevels and the frequency of normal molecular vibrational mode in (11), respectively (Fig. 1).
Taking n ~ 1019 cm–3, \({{G}_{ \bot }}{\kern 1pt} \) ~ 10–14 erg, \(\rho \approx \) 5 g/cm3 [3, 31, 32], \(a \approx 5 \times {{10}^{5}}\) cm/s, and \({{\omega }_{S}} \sim {{10}^{{10}}}{\kern 1pt} \) s–1, we find that \(\eta \sim {{10}^{{ - 5}}} \ll 1\). For this reason we can assume that \({{a}_{0}} \approx a\) in (12) and consider the right-hand side of this equation as small. Then the wave equation can be reduced from the second to the first order using the approximation of unidirectional pulse propagation with a velocity close to the linear velocity a [37]. As a result, we have
Thus, condition (10) allowed us to formally exclude from consideration the excitation of the quantum transitions \( - \leftrightarrow 0\) and \( + \leftrightarrow 0\). The analysis reduced to the consideration of the pulse field dynamics and excitation of the forbidden transition \( - \leftrightarrow + \) by the squared field via the intermediate state with \({{S}_{z}} = 0\) based on the self-consistent system of Eqs. (11) and (13).
3 UNIPOLAR AUTOWAVE
According to the above numerical estimates, the following condition is satisfied with good accuracy:
Using (14), one can exclude material variables. To this end, we assume (in the zero approximation in small parameter (14)) that \({{\omega }_{0}} = 0\) in (11). Then, on the assumption that \(U = V = 0\) and \(W = {{W}_{{ - \infty }}}\) prior to the pulsed impact on the medium (at \(t = - \infty \)), we find from (11) that
where
In this case, we find from the first expression in (11) that
Substituting (17) into (13) with allowance for the first expression in (15), we arrive at the nonlinear integro-differential wave equation
where \(\mu = 2{{\omega }_{0}}\eta {{W}_{{ - \infty }}}{\text{/}}a\).
In the case of inverse initial population of Zeeman sublevels, \({{W}_{{ - \infty }}} > 0\). Hence, \(\mu > 0\). This energy margin, as was noted above, can compensate the losses described by the last term on the right-hand side of (18).
Inverse population of Zeeman sublevels can be created, for example, by a preliminary impact of a resonant longitudinal ultrasonic pulse on paramagnetic ions [3, 28]. In this case the aforementioned van Vleck mechanism is responsible for the resonant quantum transition \( - \to + \). The population of the ground state, characterized by the effective spin projection \({{S}_{z}} = - 1\), can be additionally reduced involving the quantum transition \( - \to 0\) due to the resonant magnetic dipole interaction with the electromagnetic pulse of frequency \({{\omega }_{ + }}\) (Fig. 1).
Equation (18) (see also (16)) formally coincides with Eq. (12) from [30]. Therefore, the analysis will be performed using the approximate soliton-like solution to Eq. (18) that was found in [30]:
where
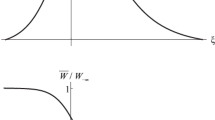
At first glance, this localized solution has all properties of a dissipative soliton. Indeed, it has not any continuous free parameters. The amplitude \({{\Omega }_{m}}\) of soliton-like unipolar pulse, its velocity \(v\), and duration \({{\tau }_{{\text{p}}}}\) take fixed values, which depend on the parameters of the medium that are determined by the coefficients of Eq. (18). At the same time, the states of the medium before and after the pulse transmission are different and have finite lifetimes; i.e., they are metastable. It follows from (15), (16), and (19) that, at \(t \to + \infty \), the dynamic parameters W and V take, correspondingly, the values \({{W}_{{ + \infty }}} = - {{W}_{{ - \infty }}}{\text{/}}2 < 0\) and \({{V}_{{ + \infty }}} = - \sqrt 3 {\kern 1pt} {\kern 1pt} {{W}_{{ - \infty }}}{\text{/}}2\). At the same time the parameter U remains negligible. Thus, the energy influx to the shear strain pulse from each paramagnetic ion is \(2\hbar {{\omega }_{0}}({{W}_{{ - \infty }}} - {{W}_{{ + \infty }}}) = \) \(3\hbar {{\omega }_{0}}{{W}_{{ - \infty }}}\). This influx is compensated by the irreversible losses that are not related to paramagnetic ions.
Since \({{W}_{{ + \infty }}} \ne 0\), the coherence induced by the transmitted pulse remains on the forbidden transition with the frequency \(2{{\omega }_{0}}\). However, as follows from (11) and (12), this coherence cannot stimulate generation of shear strain oscillations in the crystal in the absence of additional seed field. The lifetime in this superposition state is of the same order of magnitude as the time \({{T}_{2}}\) of irreversible phase relaxation on the considered transition. At \({{\omega }_{0}} \sim \) 1011 s–1 for Fe2+ ions in a MgO crystal, \({{T}_{2}}\sim \) 10–5 s [3]. In our case, for \({{\omega }_{0}}\sim \) 108 s–1 and liquid helium temperatures \(T\), the following condition is fulfilled: \(\hbar {{\omega }_{0}} \ll {{k}_{{\text{B}}}}T\), where \({{k}_{{\text{B}}}}\) is the Boltzmann constant. Here, \({{T}_{2}} \sim \omega _{0}^{{ - 2}}\) [38]. Then, in the case under consideration, we have \({{T}_{2}} \sim 10\) s. The lifetime of the initial state of paramagnetic ions, characterized by inverse population of Zeeman sublevels and zero coherence on the corresponding quantum transition, is of the same order as the energy relaxation time \({{T}_{1}}\), which is two orders of magnitude longer than \({{T}_{2}}\).
Thus, when a soliton-like pulse (19) passes through a medium, the latter undergoes a transition between two long-lived metastable states. Following the terminology accepted in [39], we will refer to the soliton-like signal (19) as a localized autowave.
Using the results of [30], we will write the threshold conditions for the input parameters of the shear strain pulse, under which this unipolar pulse can be transformed into a localized autowave (19):
Here, \({{\tau }_{0}}\) and \({{\Omega }_{0}}\) are the duration and temporal profile of the strain pulse at the input of the medium, respectively, and \({{A}_{0}}\) is obviously proportional to the pulse input energy.
Taking into consideration that \(I = 0.5\rho {{a}^{3}}\varepsilon _{{zx}}^{2}\) is the pulse intensity, we can conclude that the value \(\sigma = \rho {{a}^{3}}\varepsilon _{{zx}}^{2}{{\tau }_{{\text{p}}}}\) has the meaning of the pulse energy per unit area of the pulse cross section. Then we can write \({{A}_{0}} = {{\sigma }_{0}}{\text{/}}{{\sigma }_{c}}\), where \({{\sigma }_{0}}\) is the input pulse energy per unit area and \({{\sigma }_{c}} = 4{{\hbar }^{2}}{{\omega }_{s}}\rho {{a}^{3}}{\text{/}}G_{ \bot }^{2}\) is the value of this specific energy characteristic of the medium under consideration.
A unipolar pulse can be generated at the input of a crystalline medium due to the electrostriction (by exposing the crystal to a high-power nanosecond pulse) [6, 7].
One can easily see that the above-introduced parameter—energy per unit cross-sectional area of the formed localized autowave (19)—is \(A \equiv \omega _{s}^{{ - 1}}\int_{ - \infty }^{ + \infty } {{{\Omega }^{2}}dt} \) = \(\sigma {\text{/}}{{\sigma }_{c}} = 4\pi {\text{/}}3\).
Below we present some numerical estimates. For gigahertz frequencies \(q{{\omega }^{2}} = 0.3{\kern 1pt} \) cm–1 [40]. Having taken \(\omega = 5 \times {{10}^{9}}\) s–1, we find \(q \sim {{10}^{{ - 20}}}\) s2/cm. For the above-accepted parameters of the medium, \(\mu \sim \) 10‒2 cm–1. Then the last equality in (20) yields \({{\tau }_{{\text{p}}}} \sim {{10}^{{ - 9}}}\) s and \(q{\text{/}}{{\tau }_{{\text{p}}}} \sim {{10}^{{ - 11}}}\) s/cm \( \ll \;{\kern 1pt} 1{\text{/}}a\). It follows from here in particular that the autowave velocity is almost equal to the linear velocity of shear strain wave in the considered crystal.
The characteristic specific energy \({{\sigma }_{c}}\) at the parameter values used above can be estimated as \({{\sigma }_{c}} \sim \) 10 μJ/cm2. Since \(\sigma \sim {{\sigma }_{c}}\), the pulse intensity I can be estimated as \(I \sim \sigma {\text{/}}{{\tau }_{{\text{p}}}} \sim {{10}^{4}}\) W/cm2. Then the relative pulse distortion is \({{\varepsilon }_{{zx}}} \sim \sqrt {I{\text{/}}\rho {{a}^{3}}} \sim {{10}^{{ - 4}}}{-} {{10}^{{ - 3}}}\). On the assumption that the characteristic transverse size of elastic pulse is \(d \sim 1\) mm, the pulse power P and energy w can be found as \(P \sim I{{d}^{2}} \sim {{10}^{2}}\) W and \(w \sim P{{\tau }_{{\text{p}}}} \sim 0.1\) μJ.
Thus, the localized unipolar shear deformation autowave is a fairly high-power nanosecond signal.
4 CONCLUSIONS
It has been shown that appropriate conditions for two-photon spin-phonon transitions, similar to the Raman two-photon transitions in optics, can be formed in a paramagnetic crystal placed in an external magnetic field and a longitudinal static strain field. The role of the frequency of these transitions is played by the frequency of Zeeman splitting of effective-spin states. In the case of inverse initial population of Zeeman sublevels, a nanosecond unipolar soliton-like shear strain pulse can be formed in the crystal; this pulse was referred to as localized autowave. Here, the energy influx from paramagnetic ions is compensated by the irreversible losses caused by pulse damping because of scattering from thermal lattice vibrations, defects, and microinhomogeneities. It is important that paramagnetic ions pass from the nonequilibrium state with inverse population of Zeeman sublevels to another metastable state during the pulse transmission. Therefore, the time during which these objects can be experimentally observed is limited from above by the characteristic lifetimes of ions in these states. Estimation showed this time to be fairly long: several tens of seconds.
Threshold conditions (21) reflect the significantly nonlinear character of the formation of the localized autowave considered here.
REFERENCES
F. V. Bunkin, Yu. A. Kravtsov, and G. A. Lyakhov, Sov. Phys. Usp. 29, 607 (1986).
S. L. McCall and E. L. Hahn, Phys. Rev. Lett. 18, 908 (1967).
N. S. Shiren, Phys. Rev. B 2, 2471 (1970).
G. A. Denisenko, Sov. Phys. JETP 33, 1220 (1971).
V. V. Samartsev, B. P. Smolyakov, and R. Z. Sharipov, JETP Lett. 20, 296 (1974).
V. E. Gusev and A. A. Karabutov, Laser Optical Acoustics (Nauka, Moscow, 1991) [in Russian].
S. A. Akhmanov and V. E. Gusev, Sov. Phys. Usp. 35, 153 (1992).
S. A. Akhmanov, V. A. Vysloukh, and A. S. Chirkin, The Optics of Femtosecond Pulses (Nauka, Moscow, 1988; Am. Inst. Phys., Bristol, 1991).
F. Krausz and M. Ivanov, Rev. Mod. Phys. 81, 163 (2009).
E. M. Belenov, P. G. Kryukov, A. V. Nazarkin, A. N. Oraevskii, and A. V. Uskov, JETP Lett. 47, 523 (1988).
E. M. Belenov and A. V. Nazarkin, JETP Lett. 51, 288 (1990).
D. H. Auston, K. P. Cheung, J. A. Valdmanis, and D. A. Kleinman, Phys. Rev. Lett. 53, 1555 (1984).
S. V. Sazonov, J. Phys.: Condens. Matter 6, 6295 (1994).
A. A. Zabolotskii, JETP Lett. 76, 607 (2002).
S. V. Sazonov and N. V. Ustinov, Phys. Rev. E 73, 056614 (2006).
R. M. Arkhipov, JETP Lett. 113, 611 (2021).
R. M. Arkhipov, M. V. Arkhipov, A. V. Pakhomov, M. O. Zhukova, A. N. Tcypkin, and N. N. Rosanov, JETP Lett. 113, 242 (2021).
N. N. Rosanov, Dissipative Optical and Related Solitons (Fizmatlit, Moscow, 2021) [in Russian].
N. Akhmediev, A. Ankiewicz, J. M. Soto-Crespo, and Ph. Grelu, Int. J. Bifurc. Chaos 19, 2621 (2009).
N. A. Veretenov, N. N. Rosanov, and S. V. Fedorov, Phys. Rev. Lett. 117, 183901 (2016).
S. V. Fedorov, N. N. Rosanov, and N. A. Veretenov, JETP Lett. 107, 327 (2018).
S. K. Turitsyn, N. N. Rosanov, I. A. Yarutkina, A. E. Bednyakova, S. V. Fedorov, O. V. Shtyrina, and M. P. Fedoruk, Phys. Usp. 59, 642 (2016).
N. A. Veretenov, N. N. Rosanov, and S. V. Fedorov, Phys. Usp. 65, 131 (2022).
V. E. Lobanov, N. M. Kondratiev, and I. A. Bilenko, Opt. Lett. 46, 2380 (2021).
S. V. Sazonov, JETP Lett. 113, 592 (2021).
S. V. Sazonov, JETP Lett. 114, 104 (2021).
S. V. Sazonov, Phys. Rev. A 103, 053512 (2021).
S. V. Sazonov, JETP Lett. 114, 132 (2021).
S. V. Sazonov, Laser Phys. Lett. 18, 105401 (2021).
S. V. Sazonov, JETP Lett. 116, 22 (2022).
V. A. Golenishchev-Kutuzov, V. V. Samartsev, N. K. Solovarov, and B. M. Khabibullin, Magnetic Quantum Acoustics (Nauka, Moscow, 1977) [in Russian].
J. W. Tucker and V. W. Rampton, Microwave Ultrasonics in Solid State Physics (North-Holland, Amsterdam, 1972).
U. Kh. Kopvillem and V. R. Rizaev, Sov. Phys. JETP 38, 1147 (1974).
K. N. Baranskii, Physical Acoustics of Crystals (Mosk. Gos. Univ., Moscow, 1991) [in Russian].
V. A. Krasil’nikov and V. V. Krylov, Introduction to Physical Acoustics (Nauka, Moscow, 1984) [in Russian].
N. I. Koroteev and I. L. Shumai, Physics of High-Power Laser Radiation (Nauka, Moscow, 1991) [in Russian].
J. C. Eilbeck, J. D. Gibbon, P. J. Caudrey, and R. K. Bullough, J. Phys. A 6, 1337 (1973).
S. A. Altshuler and B. M. Kozyrev, Electron Paramagnetic Resonance (Nauka, Moscow, 1972; Elsevier, Amsterdam, 1964).
V. A. Vasil’ev, Yu. M. Romanovskii, and V. G. Yakhno, Autowave Processes (Nauka, Moscow, 1987) [in Russian].
J. de Klerk, Phys. Rev. 139, A1635 (1965).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The author declares that he has no conflicts of interest.
Additional information
Translated by Yu. Sin’kov
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sazonov, S.V. Localized Unipolar Shear Deformation Autowaves in a Nonequilibrium Paramagnet. Jetp Lett. 116, 574–579 (2022). https://doi.org/10.1134/S0021364022601919
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0021364022601919