Electronic and Spin Structure of Topological Surface States in MnBi₄Te₇ and MnBi₆Te₁₀ and Their Modification by an Applied Electric Field

The electronic and spin structure of topological surface states in antiferromagnetic topological insulators MnBi₄Te₇ and MnBi₆Te₁₀ consisting of a sequence of magnetic MnBi₂Te₄ septuple layers separated by nonmagnetic Bi₂Te₃ quintuple layers has been calculated within the density functional theory. Features characteristic of systems with different terminations of the surface (both septuple and quintuple layers) have been analyzed and theoretical calculations have been compared with the measured dispersions of electronic states. It has been shown that a band gap of about 35–45 meV, as in MnBi₂Te₄, opens at the Dirac point in the structure of topological surface states in the case of the surface terminated by a magnetic septuple layer. In the case of the surface terminated by a nonmagnetic quintuple layer, the structure of topological surface states is closer to the form characteristic of Bi₂Te₃ with different energy shifts of the Dirac point and the formation of hybridized band gaps caused by the interaction with the lower-lying septuple layer. The performed calculations demonstrate that the band gap at the Dirac point can be changed by varying the distance between layers on the surface without a noticeable change in the electronic structure. The application of an electric field perpendicular to the surface changes the electronic and spin structure of topological surface states and can modulate the band gap at the Dirac point depending on the magnitude and direction of the applied field, which can be used in applications.

INTRODUCTION

Recently, considerable research efforts in condensed matter physics have been directed to the intensive study of the electronic and spin structure features of systems with a unique combination of topological and magnetic properties, which are characterized by new nontrivial quantum effects interesting for practical applications. The quantum anomalous Hall and topological quantum magnetoelectric effects, which are based on the Hall conductivity and quantization of the magnetoelectric response, respectively, are among the most striking such effects (see, e.g., [1–5]). These topological effects are particularly pronounced in systems based on topological insulators (TIs), in which the internal magnetic field is introduced to realize the quantum anomalous Hall effect both by doping the TI with magnetic impurities (see, e.g., [6]) and by magnetic extension effects (magnetic proximity) when a magnetic layer is applied to the nonmagnetic TI surface (see, e.g., [7, 8]). Intrinsic magnetically ordered TIs, where magnetic atoms are embedded directly in the crystal structure of a formed magnetic TI, have also been successfully synthesized. This ensures the ordered arrangement of magnetic atoms inside the crystal lattice and makes it possible to significantly increase the concentration of magnetic atoms and their effect. One of the most prominent example of such a magnetically ordered TI is the antiferromagnetic TI with MnBi₂Te₄ stoichiometry. In recent years, considerable efforts have been devoted to the study of the electronic structure and magnetic properties of this TI (see, e.g., [9–18]). Simultaneously, the possibility of implementation of the quantum Hall effect in such systems was shown both theoretically [19, 20] and experimentally [21–23]. The possibility of implementing the quantum anomalous Hall effect in thin MnBi₂Te₄ layers at higher temperatures was also shown [21, 24], significantly increasing applied interest in the study of the electronic and magnetic properties of this material. After that, a series of magnetically ordered antiferromagnetic TIs with the stoichiometric composition (MnBi₂Te₄)(Bi₂Te₃)_m were successfully developed and synthesized [14, 25–29] with the modulation of the magnetic properties by means of the introduction of nonmagnetic layers between magnetic septuple layers (SLs). Each compound in this series has both common properties and unique features of the electronic structure.

The (MnBi₂Te₄)(Bi₂Te₃)_m family includes topologically nontrivial compounds such as MnBi₂Te₄ (m = 0), MnBi₄Te₇ (m = 1), MnBi₆Te₁₀ (m = 2), MnBi₈Te₁₃ (m = 3), etc., which have a layered structure consisting of magnetic MnBi₂Te₄ SLs separated by nonmagnetic Bi₂Te₃ quintuple layers (QLs). All SLs and QLs are separated by van der Waals (vdW) intervals. The neighboring magnetic layers are coupled by the antiferromagnetic interaction between magnetic Mn layers. Coupling inside each magnetic Mn layer is ferromagnetic. (For MnBi₂Te₄, magnetic SLs are coupled directly without intermediate Bi₂Te₃ QLs.) Figure 1 presents (а) the structure of the MnBi₂Te₄ SL with the arrangement of atoms and directions of magnetic moments inside the layer and (b) the general structure and directions of magnetic moments in neighboring SLs in MnBi₂Te₄(Bi₂Te₃)_m compounds with (left) m = 1 (i.e., MnBi₄Te₇) and (right) m = 2 (i.e., MnBi₆Te₁₀), which are studied in this work.

Fig. 1.

(Color online) (а) Structure of the MnBi₂Te₄ septuple layer with the arrangement of atoms and directions of magnetic moments inside the layer. (b) General structure and directions of magnetic moments inside each septuple layer (SL) and between neighboring septuple layers in MnBi₂Te₄(Bi₂Te₃)_m compounds with (left) m = 1 (i.e., MnBi₄Te₇) and (right) m = 2 (i.e., MnBi₆Te₁₀); QL marks the Bi₂Te₃ quintuple layer.

The analysis of features of the electronic and spin structure for (MnBi₂Te₄)(Bi₂Te₃)_m compounds is currently limited, particularly the representation and analysis of the spin structure of topological surface states with the perpendicular (out-of-plane) and parallel (in-plane) spin orientations to the surface, as well as changes in their electronic and spin structure in an applied electric field. The spin structure of TSSs and the band gap at the Dirac point determine the effective implementation of the quantum anomalous Hall effect (including high-temperature) in these compounds.

In this context, the aims of this work are to study the electronic and spin structure of the MnBi₄Te₇ and MnBi₆Te₁₀ compounds calculated within the density functional theory for surfaces with different terminations and to compare theoretical calculations with experimental ARPES spectra. The band gap opening at the Dirac point is estimated from measurements and is compared with calculated values under variation of the calculation parameters. We also analyze changes in the electronic and spin structure and the corresponding modification of the band gap at the Dirac point in the electric field perpendicular to the surface with various magnitudes and opposite directions, which is of interest for applications.

ANALYSIS OF FEATURES OF THE ELECTRONIC STRUCTURE AND WIDTH OF THE BAND GAP OPENING AT THE DIRAC POINT FOR THE MnBi₄Te₇ AND MnBi₆Te₁₀ SURFACES WITH DIFFERENT TERMINATIONS

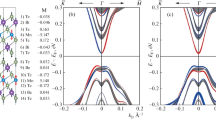
Figures 2 and 3 present the electronic and spin structure of TSSs and the nearest states in the valence and conduction bands calculated within the density functional theory for the MnBi₄Te₇ and MnBi₆Te₁₀ compounds with the surface terminated by magnetic SL (Figs. 2а, 2b, 3а, 3b), one QL (1 QL) (Figs. 2e, 2f, 3e, 3f), and two QLs (2 QLs) (Figs. 3i, 3j). The calculated spin electronic structure is presented for both the in-plane and out-of-plane spin orientations. States with opposite spin orientations in the directions k$_{{||}}$ and k$_{ \bot }$ are indicated by red and blue symbols. For comparison, the corresponding ARPES dispersion maps for these compounds under laser excitation ($h\nu = 6.3$ eV) with the surface terminated by SL, QL, and two QLs are shown in Figs. 2c, 2d, 2g, 2h, 3c, 3d, 3g, 3h, 3k, and 3l in the form of $N(E)$ (Figs. 2c, 2g, 3c, 3g, 3k) and ${{d}^{2}}N{\text{/}}d{{E}^{2}}$ (Figs. 2d, 2h, 3d, 3h, 3l). Details of the calculations are summarized in section METHODS.

Fig. 2.

(Color online) (а, b, e, f) Calculated electronic and spin structure of topological surface states and the nearest states in the valence and conduction bands for MnBi₄Te₇ in the case of the surface terminated by the (а, b) septuple layer (7–5–7–5) and (e, f) quintuple layer (5–7–5–7). The dispersion curves are plotted separately for the (a, e) in-plane and (b, f) out-of-plane spin orientations. Opposite directions in k$_{{||}}$ and k$_{ \bot }$ are shown in red and blue. (c, d, g, h) Measured dispersion maps corresponding to (а, b, e, f) represented in the form of (c, g) $N(E)$ and (d, h) ${{d}^{2}}N{\text{/}}d{{E}^{2}}$.

Fig. 3.

(Color online) (а, b, e, f, i, j) Calculated electronic and spin structure of topological surface states and the nearest states in the valence and conduction bands for MnBi₆Te₁₀ in the case of the surface terminated by the (а, b) septuple layer (7–5–5–7), (e, f) quintuple layer (5–7–5–5), and (i, j) two quintuple layers (5–5–7–5). The dispersion curves are plotted separately for the (а, e, i) in-plane and (b, f, j) out-of-plane spin orientations. Opposite directions in k$_{{||}}$ and k$_{ \bot }$ are shown in red and blue. (c, d, g, h, k, l) Measured dispersion maps corresponding to (а, b, e, f, i, j) represented in the form of (c, g, k) $N(E)$ and (d, h, l) ${{d}^{2}}N{\text{/}}d{{E}^{2}}$.

The presented results indicate that the electronic structures of TSSs for magnetic TIs MnBi₄Te₇ and MnBi₆Te₁₀ are significantly different, primarily, for the surfaces terminated by the magnetic MnBi₂Te₄ SL and by the nonmagnetic Bi₂Te₃ QL. For terminations with one or two QLs on the surface, the binding energies for the Dirac point are significantly different and the electronic structure of TSSs and states of the valence and conduction bands is more complex. The presented calculations of the electronic structure are mainly in agreement with calculations reported in [27, 30–37] and are generally confirmed by experimental data. In addition, the calculations of the spin structure of these systems are also presented in this work.

The analysis of the calculated electronic and spin structure of TSSs shows that both MnBi₄Te₇ and MnBi₆Te₁₀ samples with the surfaces terminated by the magnetic SL have the helicoidal in-plane spin structure near the $\bar {\Gamma }$ point (similar to MnBi₂Te₄ [9, 18, 38]). The band gap at the Dirac point (${{k}_{{||}}}$ = 0) opens in all presented spectra in the region of the $\bar {\Gamma }$ point in the case of the termination by the magnetic SL. According to the calculations, the band gap at the $\bar {\Gamma }$ point for MnBi₄Te₇ and MnBi₆Te₁₀ should be 42 and 36 meV, respectively, in agreement, e.g., with a theoretical estimate of 35 meV for the band gap at the Dirac point in MnBi₆Te₁₀ in [35]. These widths of the band gap for MnBi₄Te₇ and MnBi₆Te₁₀ are smaller than a Dirac band gap of 55–88 meV calculated for MnBi₂Te₄. A decrease in the gap can be due to a decrease in the exchange interaction between the neighboring Mn layers in the MnBi₄Te₇ and MnBi₆Te₁₀ compounds compared to MnBi₂Te₄. Since two nonmagnetic QLs are introduced between SLs in MnBi₆Te₁₀ (compared to one QL in MnBi₄Te₇), the band gap formed at the Dirac point in MnBi₆Te₁₀ is smaller. Agreement with experimental data is good both for the general structure of TSSs and for states in the valence and conduction bands.

The electronic and spin structure in the case of the surface terminated by the nonmagnetic QL is more complex. According to the presented experimental spectra for MnBi₄Te₇ with QL-termination, the Dirac point is shifted toward higher binding energies. In this case, an additional band gap is formed in the region of the upper Dirac cone because of the hybridization of the states of the upper QL with the states of the lower-lying SL near the Dirac point of this SL [27, 30–37]. The calculated spectra (in particular, for MnBi₄Te₇) also clearly exhibit the formation of such a hybridized band gap. Both the calculated and experimental spectra for MnBi₆Te₁₀ also demonstrate an energy shift of the point corresponding to the lower edge of the upper part of the Dirac cone. The spectrum of MnBi₆Te₁₀ samples with the surface terminated by two nonmagnetic QLs is more similar to the Dirac cone characteristic of Bi₂Te₃.

At the same time, additional states appear on both sides of the Dirac cone in the conduction band in the experimental spectra compared to the theoretical ones. These states are assumingly due to a certain hybridization of the states of the Dirac cone in the upper MnBi₂Te₄ SL with the bulk states of the lower-lying Bi₂Te₃ QL [27, 30–37]. These states are more pronounced in photoelectron measurements with laser radiation [30–34, 36, 37, 39], where photoelectrons are emitted from a much larger depth, which allows sensitivity to the contribution to photoelectron spectra of the second lower-lying QL. These states are much less manifested in measurements with synchrotron radiation with a higher energy of exciting photons (which corresponds of a smaller escape depth of photoelectrons) [27], although the position of the Dirac point in measurements with synchrotron and laser radiation is almost the same. These hybridization effects are the most clearly manifested in the cases of the surface termination by the Bi₂Te₃ QL in the formation of the pronounced hybridized band gap in the region of states of the upper Dirac cone in the region of the edge of valence states near the low-lying SL. These hybridization effects in the case of the surface termination by two QLs are less pronounced. Another interpretation of the appearance of additional states on both sides of states of the upper Dirac cone is the formation of the corresponding Rashba states and their hybridization with TSSs (see [33, 40]).

COMPARISON WITH EXPERIMENTAL DATA

Figure 4 shows ARPES dispersion maps of the electronic states measured for the MnBi₄Te₇ surface terminated by the magnetic SL, corresponding distributions of the electron density of states measured directly at the $\bar {\Gamma }$ point, and the band gap between the upper and lower cones of topological surface states for two samples. It is worth noting that the formation of the band gap at the Dirac point is directly due to the reversal of the out-of-plane spin polarization between the upper and lower Dirac cones at the Dirac point (see the out-of-plane spin structure in Figs. 2 and 3), which is the most pronounced for the SL-terminated surface. The spectra were measured using laser radiation with a photon energy of 6.3 eV at a temperature of 10 K, which is below the Néel temperature. Figures 4a–4c and 4f–4h present the dispersion maps in the form of (а, f) $N(E)$ and (b, g) ${{d}^{2}}N{\text{/}}d{{E}^{2}}$ (for the better visualization of the gap at the Dirac point (${{k}_{{||}}} = 0$)), as well as (c, h) the more detailed map near the Dirac point. The corresponding electron densities of states measured directly at the $\bar {\Gamma }$ point are shown by red squares and thick solid lines in Figs. 4d and 4i together with their spectral components given by thin solid lines. The energy positions of these spectral components correspond to the edges of the band gap opening at the Dirac point. Figures 4e and 4j present the band gap between the upper and lower cones of TSSs, which is obtained from similar decompositions into spectral components, versus ${{k}_{{||}}}$ varying in the positive and negative direction with respect to the $\bar {\Gamma }$ point. The presented dependences are approximated by the model curve $E \sim {{({{\alpha }^{2}}{{k}^{2}} + {{\Delta }^{2}})}^{{1/2}}}$, where Δ is the band gap at the Dirac point, which is characteristic of the Dirac cone with a band gap. This approach allows the reduction of an error in the estimated band gap. The minimum energy splitting at the $\bar {\Gamma }$ point corresponds to the band gap at the Dirac point.

Fig. 4.

(Color online) Measured dispersion maps of the electronic states for the MnBi₄Te₇ surface terminated by the magnetic septuple layer represented in the form of (а)$N(E)$, (b) ${{d}^{2}}N{\text{/}}d{{E}^{2}}$, and (c) the more detailed map near the Dirac point. (d) Corresponding distributions of the electron density of states measured directly at the $\bar {\Gamma }$ point where ${{k}_{{||}}}$ = 0 with decomposition into spectral components (solid lines are states of the Dirac cone indicating the band gap). (e) Band gap between the upper and lower cones of topological surface states versus ${{k}_{{||}}}$ varying in the positive and negative direction with respect to the $\bar {\Gamma }$ point. (f–j) Same as (a–e) but for another sample.

The experimental data presented in Fig. 4 indicate that the surface termination by the magnetic MnBi₄Te₇ SL is indeed characterized by the opening of the band gap (about 35–42 meV) at the Dirac point. The measured gap at the Dirac point corresponds to a calculated band gap of about 42 meV. Figure 5 shows the gap under the variation of the vdW distance between the septuple and quintuple layers in the system. It is noteworthy that the authors of [32–34] suggest the absence of the band gap directly at the Dirac point, whereas the existence of the gap at the Dirac point in various TIs (MnBi₂Te₄)(Bi₂Te₃)_m was demonstrated both theoretically [27, 35–37] and experimentally [27, 29, 39]. However, the out-of-plane spin structure for surfaces terminated by the magnetic SL in both MnBi₄Te₇ and MnBi₆Te₁₀ shown in Figs. 2 and 3 exhibits the pronounced reversal of the spin polarization at the edges of the Dirac band gap directly at the $\bar {\Gamma }$ point. Such out-of-plane spin polarization is due both to the mass term in the Hamiltonian and to the formation of the band gap at the Dirac point. It is much more difficult to separate the out-of-plane spin polarization between the upper and lower cones near the Dirac point in the case of the surface terminated by the nonmagnetic QL because of strong overlapping with branches of the valence band.

Fig. 5.

(Color online) (a1–a4) Change in the electronic structure for the MnBi₄Te₇ surface terminated by the magnetic septuple layer under the variation of the van der Waals distance between the septuple and quintuple layers. (b1–b4, c1–c4) Same as in (a1–a4) but for MnBi₆Te₁₀ under the variation of the van der Waals distance (b1–b4) between the quintuple layers and (c1–c4) between the quintuple and septuple layers. (d) Corresponding change in the band gap at the Dirac point for all three calculated variants.

DEPENDENCE OF FEATURES OF THE ELECTRONIC STRUCTURE ON THE CALCULATION PARAMETERS

It is worth noting that different vdW distances between SLs and QLs and different interatomic distances in layers are used in different reported calculations. This difference in the used parameters is responsible for possible small differences in features of the calculated electronic spectra, including difference in the band gap at the Dirac point. The theoretical dispersion curves presented in Figs. 2 and 3 were calculated for the atomic structure of the unit cell of MnBi₄Te₇ used in [9, 17, 18] and with the vdW distances between SLs and QLs taken as the averages of the values used in [25, 27]. To determine the possible effect of the variation of the vdW distances on the details of the electronic structure and on the band gap at the Dirac point, we additionally performed comparative calculations with the structural parameters for SLs taken from [41], with increased and decreased vdW distances between QLs and SLs.

Figures 5а1–5а4 show the calculated electronic structure for MnBi₄Te₇ with the surface terminated by the magnetic SL and the band gap at the Dirac point under the variation of the vdW distance between SLs and QLs in the entire volume of the sample with respect to a vdW distance of 2.726 Å taken as the a-verage of the vdW distances used in [25, 27]. The structural parameters of SLs were taken from [41]. Figures 5b1–5b4 and 5c1–5c4 show the similarly calculated the electronic structure for the MnBi₆Te₁₀ surface also terminated by the magnetic SL under the variation of the vdW distance between QLs and between QLs and SLs, respectively. The resulting band gaps at the Dirac point calculated with various vdW distances are shown in Fig. 5d for all three calculated variants.

The presented results show that the gap at the Dirac point under the variation of the vdW distance for MnBi₄Te₇ within $\pm$4% can change from 52 to 31 meV. Similar estimates for MnBi₆Te₁₀ demonstrate possible changes in the band gap at the Dirac point from 49 to 13 meV under the variation of the distance between QLs and from 31 to 36 meV under the variation of the distance between QLs and SLs, respectively. The band gap at the Dirac point under the variation of all vdW distances within ±2% changes from 23 to 47 meV. Differences in the presented vdW distances in [25, 27] are no more than ±(2–4)%. This variation leads to a possible change in the gap at the Dirac point primarily from 30 to 50 meV, which is in the range of the measured gaps at the Dirac point reported in this and other works. No significant changes in the electronic structure in these compounds are observed.

Comparison and analysis indicate that the calculated electronic and spin structures presented in Figs. 2 and 3 for MnBi₄Te₇ and MnBi₆Te₁₀ with different surface terminations, as well as their fundamental features, slightly depend on the variation of the vdW distances and are in agreement with previously reported data.

CHANGE IN THE ELECTRONIC STRUCTURE OF MnBi₄Te₇ AND MnBi₆Te₁₀ IN THE APPLIED ELECTRIC FIELD

We additionally studied the possibility of change in the band gap under the variation of the external factors acting on the samples. The electronic and spin structures of TSSs calculated for the MnBi₄Te₇ and MnBi₆Te₁₀ surfaces terminated by the magnetic SL in the applied electric field perpendicular to the surface with various strengths (from +0.11 to –0.34 V/Å) and in opposite directions are shown in Figs. 6а1–6а8 and 6b1–6b8, respectively, for the (a1, a3, a5, a7 and b1, b3, b5, b7) in-plane and (a2, a4, a6, a8 and b2, b4, b6, b8) out-of-plane spin orientations. The contributions from states localized primarily in the first surface SL are shown. The opposite directions of the spin component (S_x and –S_x) and (S_z and –S_z) for the orientations parallel and perpendicular to the surface are shown in red and blue, respectively.

Fig. 6.

(Color online) Calculated electronic and spin structure with the in-plane and out-of-plane spin orientations for the (a1–a8) MnBi₄Te₇ and (b1–b8) MnBi₆Te₁₀ surfaces terminated by the magnetic septuple layer in the electric field perpendicular to the surface with strengths from +0.11 to –0.34 V/Å. The Dirac point and band gap at the Dirac point are marked by circles.

The presented spectra demonstrate that the application of the electric field results in the energy shift of the topological states of the Dirac cone with respect to the states in the valence and conduction bands in both for MnBi₄Te₇ and MnBi₆Te₁₀ and this shift depends on the direction and magnitude of the applied field. The  band gap at the Dirac point also changes. The  applied electric field with the “negative” direction reduces the Dirac band gap, which almost disappears in both MnBi₄Te₇ and MnBi₆Te₁₀ at an electric field strength of −0.34 V/Å. The position of the Dirac point and the corresponding gap are marked by circles in Fig. 6 for better visualization. A similar behavior of the gap at the Dirac point under the application of the electric field was also observed in MnBi₂Te₄ [18, 38], where a higher strength of the applied electric field was required to almost vanish the band gap.

It is noteworthy that the helicoidal character of the in-plane spin structure (i.e., opposite directions of spins for opposite k_|| directions near the $\bar {\Gamma }$ point) holds for both MnBi₄Te₇ and MnBi₆Te₁₀ under any variations of the applied electric field. The reversal of the out-of-plane spin structure at the edges of the band gap at the Dirac point also holds for all strengths of the applied electric field to almost zero band gap. This assumingly implies the possibility of the purposeful change in the physicochemical properties of antiferromagnetic TIs MnBi₄Te₇ and MnBi₆Te₁₀ by modulating the band gap at the Dirac point through the application of the external electric field.

CONCLUSIONS

The electronic and spin (in-plane and out-of-plane) structure of topological surface states and nearest states in the valence and conduction bands for MnBi₄Te₇ and MnBi₆Te₁₀ samples with the surface terminated by the magnetic MnBi₂Te₄ septuple layer and by the nonmagnetic Bi₂Te₃ quintuple layer have been calculated within the density functional theory. It has been shown that a gap of about 42 and 36 meV in MnBi₄Te₇ and MnBi₆Te₁₀, respectively, opens at the Dirac point in the band structure of topological surface states in the case of the surface terminated by the magnetic septuple layer. The calculations correlate with ARPES measurements. It has been shown that the variation of the van der Waals distance between layers on the surface within ±4% results in the variation of the band gap at the Dirac point within 30–50 meV for both systems, which is in agreement with measured values. No significant changes in the electronic structure are observed. Application of an electric field perpendicular to the surface leads to different energy shifts of the cone of Dirac states and states of the valence and conduction bands. The applied electric field changes the band gap at the Dirac point and the gap at the Dirac point is almost closed at an electric field strength of –0.34 V/Å, which can be used to modulate the magnetic and physicochemical properties of these magnetic topological insulators.

The calculated spectra demonstrate the in-plane helicoidal spin structure of topological surface states inverse to $\pm {\kern 1pt} {{k}_{{||}}}$ and the out-of-plane spin structure inverse to the edge of the gap at the Dirac point, which is characteristic of magnetic topological insulators.

METHODS

The surfaces under study were represented in the calculations by repeated slabs composed of four ${\text{MnB}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{\text{4}}}}$ SLs and four or eight${\text{B}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{\text{3}}}}$ QLs in case of the ${\text{MnB}}{{{\text{i}}}_{{\text{4}}}}{\text{T}}{{{\text{e}}}_{{\text{7}}}}$ or ${\text{MnB}}{{{\text{i}}}_{{\text{6}}}}{\text{T}}{{{\text{e}}}_{{{\text{10}}}}}$ structure, respectively. The hexagonal lattice parameter a = 4.33 Å and the parameter c were chosen such that interlayer vdW distance was d_vdW = 2.73 Å as for the ${\text{MnB}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{\text{4}}}}$ structure [18, 38]. The slabs were separated by a 12-Å vacuum gap.

The electronic structure of the interfaces was calculated with the OPENMX software package [42], implementing the completely relativistic electron d-ensity functional method with a norm-conserving pseudopotential [43] and pseudoatomic orbitals Mn6.0-$s3p3d2$, Te7.0-$s3p3d2f1$, and Bi8.0-$s3p3d2f1$ as the basis functions [44–46]. The notation of orbitals for, e.g., Mn means that the s and p orbitals are represented by three primitive orbitals, the d-orbital is represented by two primitive orbitals, and the cutoff radius is 6.0 a.u. The calculations were performed with the PBE version of the generalized gradient approximation [47]. The real-space integration grid was determined by a cutoff energy of 200 Ry, and a mesh of 9 × 9 k points was used in the reciprocal space for the division of the surface Brillouin zone. The total energy convergence criterion was 1.4 × 10^–5 eV. To correct Mn d states, we used the DFT + U method [48] in the Dudarev scheme [49] with the parameter U = 5 eV [18]. The external electric gradient along the normal to the surface was specified by placing an additional charge in the vacuum region together with vacuum–slab–metal boundary conditions within the effective screening medium method [50] in order to avoid the Coulomb interaction between the slabs.

Dispersion maps were measured at the μ-Laser ARPES setup at the HiSOR center (Hiroshima, Japan) under photoexcitation by laser radiation with an energy of $h\nu = 6.3$ eV. The spatial resolution was about 5 μm (determined by the size of the focused laser spot). A Scienta R4000 energy analyzer mounted at an angle of 50° to the incident photon beam was used. Clean sample surfaces were obtained by cleavage in ultrahigh vacuum. The pressure in all photoemission experiments was less than 1 × 10^–11 mbar.