Manifestations of Electron–Nuclear Interactions in the High-Frequency ENDOR/ODMR Spectra for Triplet Si–C Divacancies in ¹³C-Enriched SiC

The frequencies of electron–nuclear interactions with ¹³C and ²⁹Si nuclei on remote coordination spheres are determined in triplet spin centers in the form of neutral V_Si–V_C divacancies in a silicon carbide crystal of the hexagonal polytype 6H–SiC enriched tenfold in the ¹³C isotope. High-frequency electron–nuclear double resonance and optically detected magnetic resonance under conditions of optical alignment of spins are used. Oscillations of the electron spin density on ²⁹Si and ¹³C nuclei are found. Nuclear magnetic resonance transitions at Larmor and close-to-Larmor frequencies of ¹³C and ²⁹Si cause giant changes in the populations of spin sublevels with the transformation of these resonances into electron paramagnetic resonance and optical signals.

Silicon carbide (SiC) is widely used in electronic devices with the possibility of using them under extreme environmental conditions. Silicon carbide has two families of spin color centers with S = 1 and 3/2, where the optical alignment of the populations of spin levels is possible. The unique magneto-optical properties provide the possibility of the optical manipulation of electron and nuclear spins under environmental conditions and make it possible to apply these spin centers as a material platform for spintronics, sensors, quantum information processing, and the development of hybrid quantum systems [1–22]. In this work, we consider a family of triplet $(S = 1)$ color centers that are neutral divacancies in the form of a covalently bound pair of V_Si and V_C vacancies [1, 2, 10, 12]. The symmetry of these centers is due to the direction of the Si–C bond, and the fine structure splitting for these centers is in the gigahertz range, similar to that in NV centers in diamond [12, 23].

The main spin phenomena in SiC are largely determined by the ²⁹Si and ¹³C isotopes with nuclear magnetic moments, although the contents of these isotopes are 4.7% and 1.1%, respectively. For many quantum applications of spin centers in SiC, it is important to fix the magnitudes (frequencies) of electron–nuclear interactions, and the low content of isotopes with nuclear magnetic moments often makes these measurements difficult. Nevertheless, these frequencies are necessary for controlling nuclear and electron spin states when using spin centers as sensors, qubits, and to design gyroscopes on nuclear spins. For this reason, we used ¹³C-enriched (~12%) SiC crystals in order to determine them.

The possibility of using ¹³C and ²⁹Si nuclear spins as long-term memory is considered in a number of algorithms for applying spin centers in SiC in quantum information processing, e.g., [12]. In this work, electron–nuclear double resonance (ENDOR) is used to obtain the frequencies of hyperfine interactions of the electron spin with the nuclear magnetic moments of ¹³C and ²⁹Si isotopes, including those with nuclei far from the location of the spin center. An important task for the use of spin centers is to elucidate the effect of a high content of an isotope with a nuclear magnetic moment (more than a tenfold increase in the ¹³C content in these studies) on the relaxation characteristics of these centers.

Nominally undoped ¹³C-enriched (~12%) n-type 6H–SiC crystals were grown by the sublimation sandwich method [24]. The samples were irradiated with a ~10¹⁸-cm^–2 fast neutron beam at room temperature and were then subjected to 30-min isochronous annealing at a temperature of 700°С. The crystals were split away in the form of plates with a known crystallographic orientation with the possibility of the sample rotation in a magnetic field in given planes.

Electron paramagnetic resonance (EPR) and optically detected magnetic resonance (ODMR) experiments were performed at a radio spectroscopy complex developed at the Ioffe Institute, including a high-frequency EPR/ODMR spectrometer in the 94 GHz band (W band) using a closed-loop magneto-optical cryostat with an operating temperature range of 1.5–300 K and a wide magnetic field range of –7 to 7 T with transition through the zero magnetic field value. The complex also includes an ODMR spectrometer based on a confocal optical microscope [25]. Optically detected magnetic resonance signals were recorded at various temperatures up to room temperature, using synchronous detection with the application of a static magnetic field and a low-frequency modulation magnetic field.

The EPR spectrum (X range, 9.4 GHz, $T = 300{\kern 1pt}$K) of a classical isolated negatively charged ${\text{V}}_{{{\text{Si}}}}^{ - }$ silicon vacancy $(S = 3{\text{/}}2)$ [26], which is shown in Fig. 1a, was recorded in order to determine the ¹³C isotope content directly in the 6H–SiC crystal lattice. The black dashed line shows the simulated EPR spectrum for the 6H–SiC crystal containing ~12% of the ¹³C isotope and with the natural content of the ²⁹Si isotope. For comparison, the blue dotted line shows the simulated EPR spectrum for the 6H–SiC crystal with the natural ¹³C and ²⁹Si isotopic contents. The hyperfine transitions for the interaction with the four nearest carbon atoms C_NN are indicated: carbon atom 1 is located along the c axis of the crystal, and three atoms 2–4 are located at equivalent positions along the bonds rotated by 70° from the c axis. These transitions are extremely intense in the ¹³C-enriched sample, but they are also visible in the simulated EPR spectrum in the crystal with the natural isotopic content. In the latter case, intense satellites from the interaction with 12 silicon atoms in the second coordination sphere with respect to the silicon vacancy are observed and denoted as Si_NNN, where NNN stands for next nearest neighbors. The hyperfine interaction structure for ²⁹Si is about 9 MHz (~0.3 mT) [27].

Fig. 1.

(Color online) (a) EPR spectrum of the isolated negatively charged ${\text{V}}_{{{\text{Si}}}}^{ - }$ silicon vacancy in the ¹³C-enriched (~12%) 6H‒SiC crystal recorded at a frequency of 9.4 GHz. Dashed lines show simulated EPR spectra described in the main text. (b) Pulse sequences for recording ESE and ENDOR spectra in the 94 GHz band. (c) Schematic representation of the 6H–SiC crystal lattice. One divacancy configuration (k1k1) is shown. Silicon and carbon atoms located in the environment of a silicon vacancy included in the V_Si–V_C divacancy are indicated. It is conditionally shown that one isotope with a nuclear magnetic moment enters the divacancy environment.

Figure 1b shows the pulse sequences used to record the EPR and ENDOR spectra by electron spin echo (ESE) in the 94 GHz band; the optimal π/2–τ–π sequence is 36–280–72 ns. Electron–nuclear double resonance measurements were carried out on an EPR Elexsys 680 spectrometer (Bruker) at a frequency of 95 GHz. The principle of ENDOR recording is based on the use of a high-energy EPR signal to the detect low-energy nuclear magnetic resonance (NMR) quanta, which makes it possible to increase the sensitivity of NMR recording by orders of magnitude and to study small energy splittings that are not allowed in conventional EPR and simply lead to line broadening. Electron–nuclear double resonance was recorded in a pulsed mode; for this reason, most of the measurements were performed in the ESE mode.

Figure 1c shows the structure of the 6H–SiC crystal lattice, which includes two quasi-cubic (k1, k2) and hexagonal (h) Si and C positions. Three configurations of V_Si–V_C neutral divacancies oriented along the c axis are possible: (k1k1), (k2k2), (hh), the so-called P6 centers [28], and a set of divacancies (k1k2), (k1h), and (k2h) are P7 centers rotated by 70° from the c axis [28]. The P6 and P7 families have the triplet ground states of a neutral Si–C divacancy and are characterized by C3v and C1h symmetries, respectively. Figure 1c shows only one divacancy configuration (k1k1), denoted below as ${\text{P}}6{\kern 1pt} '$; the other configurations can be easily obtained using the depicted part of the crystal lattice. An isolated negatively charged ${{{\text{V}}}_{{{\text{S}}{{{\text{i}}}^{ - }}}}}$ vacancy is also highlighted in Fig. 1c [26], the EPR spectrum of which is shown in Fig. 1а. This vacancy is characterized by a zero fine structure parameter, $D = 0$ [29] and exhibits no unique spin properties in the form of optically induced spin alignment. Carbon and silicon atoms, which are located in the surrounding of a silicon vacancy entering the V_Si–V_C divacancy marked in Fig. 1c as ${\text{P}}6{\kern 1pt} '$, are denoted as C_NN, Si_NNN, C_III, and Si_IV.

Figure 2 shows the orientation dependences of the ESE-detected EPR spectra of neutral V_Si–V_C divacancies in the ¹³C-enriched (~12%) 6H–SiC crystal under continuous optical laser excitation at a wavelength of 808 nm, a temperature of 150 K. The black line shows the EPR spectrum without optical excitation close to B || c (θ = 0°) orientation. It can be seen that all EPR lines without laser excitation have the same phase since they characterize the optical absorption of the microwave energy, while optical excitation leads to the phase inversion for a number of transitions, which is explained by emission instead of absorption of the microwave energy. The inset shows the microwave emission and absorption lines on an enlarged scale close to θ = 0° orientation, where the ¹³C hyperfine structure is clearly seen for two P6 centers (${\text{P}}6{\kern 1pt} '$ and ${\text{P}}6{\kern 1pt} ''$) in the form of transitions for the interaction with the nearest three carbon atoms 2–4 located in the equivalent positions along the bonds rotated by θ = 70° from the c axis (see Fig. 1c). The EPR spectra of neutral V_Si–V_C divacancies rotated by 70° from the c axis (P7 centers) appear in the θ = 70° orientation.

Fig. 2.

(Color online) Orientation dependences of the ESE-detected EPR spectra of the neutral V_Si–V_C divacancy in the ~12% ¹³C-enriched 6H–SiC crystal under continuous optical laser excitation as described in the main text. Two ODMR spectra recorded in the same sample as the electron spin echo spectra are shown in red. All spectra were recorded at a frequency of 94 GHz (W band).

Two ODMR spectra recorded in the same sample at two orientations are shown in red. Signals in the region of $g = 2$ (in the magnetic field range of 3.347–3.357 T) belong to the family of S = 3/2 spin centers and will be considered later. The phase of the ODMR lines is the same for both transitions, although these lines correspond to microwave absorption and emission. Thus, microwave absorption and emission lead to the same changes in the photoluminescence intensity of spin centers.

The ground state of a neutral V_Si–V_C divacancy in SiC is described by the spin Hamiltonian [12]

$$\begin{gathered} \hat {H} = {{g}_{e}}{{\mu }_{{\text{B}}}}{\mathbf{B}} \cdot \hat {\mathbf{S}} + D[\hat {S}_{z}^{2}-(1{\text{/}}3)S(S + 1)] \\ + E[\hat {S}_{x}^{2}-\hat {S}_{y}^{2}] + {{\Sigma }_{i}}(\hat {\mathbf{S}} \cdot {{{\mathbf{A}}}_{i}} \cdot {{\hat{\mathbf{I}}}_{i}}-{{g}_{{{\text{Ni}}}}}{{\mu }_{{\text{N}}}}{\mathbf{B}} \cdot {{\hat{\mathbf{I}}}_{i}}). \\ \end{gathered} $$

(1)

Here, ${{g}_{e}}$ ~ 2.0 is the isotropic electron g-factor; μ_B is the Bohr magneton; Ŝ is the electron spin operator with $S = 1$; A_i is the tensor describing the hyperfine interaction with the i-th Si or C atom; Î_i is the nuclear spin operator for the i-th ²⁹Si $({{I}_{{{\text{Si}}}}} = 1{\text{/}}2)$ or ¹³C $({{I}_{{\text{C}}}} = 1{\text{/}}2)$ nucleus located in different coordination spheres with respect to the positions of the V_Si–V_C divacancy; g_Ni is the g-factor of the i-th nucleus (it is negative for ²⁹Si and positive for ¹³C); ${{\mu }_{{\text{N}}}}$ is the nuclear magneton; the first term describes the Zeeman interaction of electrons; the second and third terms reflect the fine structure caused by the interaction with the crystal field; E is zero and nonzero for P6 and P7 centers, respectively; and the last term describes the hyperfine structure in the EPR and ENDOR spectra, where the first part of the sum corresponds to the hyperfine interaction and the second part describes the nuclear Zeeman interaction for ²⁹Si and ¹³C nuclei. The hyperfine interactions in the first and second spheres with respect to the Si vacancy are partially resolved in the EPR spectra.

The S = 1 ground state without an external magnetic field $(B = 0)$ is split due to the axial crystal field with a fine structure parameter D; splitting between sublevels ${{M}_{S}} = 0$ and ${{M}_{S}} = \pm 1$ is $\Delta = D$. Optical excitation changes the populations (alignment) of the divacancy spin states in SiC. As a result, the ${{M}_{S}} = 0$ level is populated excessively and the ${{M}_{S}} = \pm 1$ levels are depleted (inset of Fig. 2). The change in the level populations caused by the resonant microwave radiation strongly changes the photoluminescence intensity. This effect allows the optical detection of magnetic resonance. The ODMR technique provides a huge increase in the sensitivity, up to the ability to record single spins [10, 11, 23].

The fine structure parameters of the triplet centers considered in this work are given in [28, 30, 31]. These works present various conflicting models, which were revised and finally established as neutral V_Si–V_C divacancies in the triplet ground state in 6H–SiC [1]. It was shown that the ground state corresponds to $S = 1$, and, as a result, the divacancy in the SiC lattice is neutral; i.e., there are four electrons on bonds for carbon and silicon vacancies. Later, the neutral divacancy model was confirmed in 4H–SiC [2]. The D parameters for the P6 and P7 families, which were found in different works, basically coincide, despite the difference in the interpretation of the structure of these centers. In our experiments for ${\text{P}}6{\kern 1pt} '$ and ${\text{P}}6{\kern 1pt} ''$, the parameter D is $\sim {\kern 1pt} 440 \times {{10}^{{ - 4}}}{\kern 1pt}$ and $\sim {\kern 1pt} 430 \times {{10}^{{ - 4}}}$ cm^–1, respectively.

Electron–nuclear double resonance transition frequencies determined by selection rules, $\Delta {{M}_{S}} = 0$ and $\Delta {{m}_{I}} = \pm 1$, are given by formulas [12]:

$${{\nu }_{{{\text{ENDORi}}}}} = {{h}^{{ - 1}}}{\text{|}}{{M}_{S}}[{{a}_{i}} + {{b}_{i}}(3\mathop {\cos }\nolimits^2 \theta - 1)] - {{g}_{{{\text{Ni}}}}}{{\mu }_{{\text{N}}}}B{\text{|}},$$

(2)

where ${{a}_{i}}$ and ${{b}_{i}}$ are the isotropic and anisotropic components of the hyperfine interaction with the i‑th nucleus, respectively; θ is the angle between the external magnetic field B and the hyperfine interaction tensor; and g_Niμ_NB/h is the Larmor frequency f_L. The components of the hyperfine interaction tensor can be expressed in terms of the isotropic and anisotropic components as ${{A}_{\parallel }} = a + 2b$ and ${{A}_{ \bot }} = a - b$ with axial symmetry with respect to the axis of the p function. Here, $a\; = \;(8\pi {\text{/}}3){{g}_{e}}{{\mu }_{{\text{B}}}}{{g}_{{\text{N}}}}{{\mu }_{{\text{N}}}}{\text{|}}{{\Psi }_{{2s}}}(0){{{\text{|}}}^{2}}$ and b = $(2{\text{/}}5){{g}_{e}}{{\mu }_{{\text{B}}}}{{g}_{{\text{N}}}}{{\mu }_{{\text{N}}}}\langle r_{{2p}}^{{ - 3}}\rangle$, where Ψ is the wavefunction of the unpaired electron; i.e., the spin density on the ligand nuclei can be unambiguously determined in terms of the a and b values.

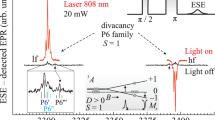
Figure 3 shows ESE-detected ENDOR spectra of V_Si–V_C divacancies in a ¹³C-enriched (~12%) 6H–SiC crystal under continuous optical excitation with an 808-nm laser at a temperature of 150 K. The ESE-detected EPR spectrum close to B || c (θ = 0°) orientation is on the right. The ENDOR spectra denoted as lf and hf correspond to the low-field and high-field EPR transitions shown on the right, respectively. There is a mirror reflection of the ENDOR lines caused by the hyperfine interactions with ¹³C and ²⁹Si located in different coordination spheres with respect to divacancy, recorded by low-field and high-field transitions. The hyperfine interactions with ²⁹Si and ¹³C nuclei are uniquely separated by the selective population of fine structure levels with certain M_S values. The signs of these interactions and, as a consequence, the signs of the oscillating spin density on the ²⁹Si and ¹³C nuclei are determined. The hyperfine interaction values with ²⁹Si and ¹³C nuclei are determined, which can be used as long-term memory in a number of quantum information processing algorithms (see, e.g., [32]).

Fig. 3.

(Color online) Electron spin echo detected ENDOR spectra of the neutral V_Si–V_C divacancy, ${\text{P}}6{\kern 1pt} '$, in the ¹³C-enriched (~12%) 6H–SiC crystal in the range of 94 GHz under continuous optical laser excitation. High-field (hf) and low-field (lf) EPR lines of ${\text{P}}6{\kern 1pt} '$ centers are shown on the right. The insets show the ENDOR lines on an enlarged scale detected near the Larmor frequencies of ¹³C and ²⁹Si. The rightmost inset shows the angular dependence of the hyperfine structure for one of the groups of the coordination sphere C_III.

A distinctive feature of the ENDOR spectra is the observation of intense signals at the Larmor frequencies of ¹³C and ²⁹Si; i.e., NMR transitions on remote spheres from the divacancy with $S = 1$ strongly change the populations of the spin sublevels of the center, which is reflected in changes in the ESE intensity. Insets of Fig. 3 show the ENDOR lines on an enlarged scale, which are recorded in the region of the Larmor frequencies of ¹³C and ²⁹Si. The rightmost inset of Fig. 3 shows the angular dependence of the hyperfine structure (HFS) for one of the groups of the coordination sphere C_III.

According to the proposed neutral divacancy model with $S = 1$, the hyperfine interactions are mainly determined by the silicon vacancy with three carbon atoms C_NN nos. 2–4 in the nearest environment (one carbon atom no. 1 located along the c axis of the crystal is absent) located in equivalent positions along the bonds rotated by 70° from the c axis. The inset of Fig. 2 shows satellites caused by the hyperfine interactions with three carbon atoms, denoted as nos. 2–4 in Fig. 1c. We note that the EPR spectrum in Fig. 1a for an isolated (dark) silicon vacancy with $S = 3{\text{/}}2$ also demonstrates the interaction with carbon atom no. 1, which is absent in the divacancy.

Table 1 presents the hyperfine interaction with ¹³C and ²⁹Si nuclei, surrounding the neutral V_Si–V_C divacancy, denoted as ${\text{P}}6{\kern 1pt} '$ and ${\text{P}}6{\kern 1pt} ''$. According to the EPR data, the hyperfine interaction with three carbon atoms located in the nearest environment of the silicon vacancy, which is a part of the divacancy, is almost axisymmetric with respect to the bond direction; for this reason, the parameters are given parallel to the bond (A$_{\parallel })$ and perpendicular to the bond (A$_{ \bot }$). The hyperfine interaction constant is determined according to the formula $A = (A_{\parallel }^{2}{{\cos }^{2}}\theta + A_{ \bot }^{2}{{\sin }^{2}}\theta {{)}^{{1/2}}}$.

Table 1. Hyperfine interactions with ¹³C and ²⁹Si nuclei surrounding neutral V_Si–V_C divacancies with spin $S = 1$ denoted as ${\text{P}}6{\kern 1pt} '$ and ${\text{P}}6{\kern 1pt} ''$ in 6H–SiC. The hyperfine interaction with three C atoms located in the nearest environment (NN) of the silicon vacancy, which is a part of the divacancy, has symmetry close to axial along the Si–C bond; for this reason, the parameters are given parallel to the bond (${{A}_{\parallel }}$) and perpendicular to the bond (${{A}_{ \bot }}$). The structure of the ${\text{P}}6{\kern 1pt} '$ center and the notations of C and Si atoms are given in Fig. 1c. Groups of lines belonging to the same type of positions of carbon atoms are marked in bold

The structure of the ${\text{P}}6{\kern 1pt} '$ center and the notation of C and Si atoms are given in Fig. 1c. The negative spin density corresponds to the positive hyperfine splitting values for ²⁹Si, and the positive spin density corresponds to positive hyperfine splitting values for ¹³C (the reverse statement is also true). We did not analyze the complete orientation dependences of the ENDOR signals, since the EPR lines for different transitions in the divacancy at large angle values begin to overlap both with each other and with the EPR lines of other spin centers. Nevertheless, in Table 1, we present the values of hyperfine interactions with various coordination spheres obtained from the ENDOR spectra. It can be seen that a number of signals have a strong anisotropy, and the difference in signs can also provide information for identifying the positions of ¹³C and ²⁹Si atoms. It is necessary to carry out theoretical calculations to substantiate the observed hyperfine interactions, which is beyond the scope of this work.

The effective impact of NMR at the Larmor frequencies of ¹³C and ²⁹Si on the ESE signal, which is directly related to the change in the populations of the electron spin levels, and, as a result, the transformation of NMR into optical signals provides wide opportunities for the applications of silicon carbide in sensors and quantum computing and for designing quantum gyroscopes. Similar effects have been observed for NV centers in diamond, which also have a triplet ground state, as well as divacancies, in which nuclear magnetic moments are used for long-term recording of information and in designing gyroscopes. For such applications, SiC enriched in isotopes with magnetic moments in fixed fractions is necessary, since most applications are based on the properties of the nuclear magnetic moments of ¹³C and ²⁹Si isotopes. In this case, the difference in the signs of the ¹³C and ²⁹Si magnetic moments can play an important role, since an effective compensation of unwanted rotations of the nuclei is expected when they are used for the development of gyroscopic devices. Parallel recording of ODMR in ¹³C-enriched (~12%) 6H–SiC indicates that any changes in the populations of the electron spin sublevels change the luminescence intensity of the spin centers.

CONCLUSIONS

The electron–nuclear interactions with carbon ¹³C and silicon ²⁹Si nuclei have been determined by high-frequency pulsed EPR and ENDOR on remote shells for neutral divacancies with spin $S = 1$ under conditions of optically induced spin alignment in 6H–SiC enriched tenfold in the ¹³C isotope. The hyperfine interactions with ¹³C and ²⁹Si nuclei are uniquely separated owing to the selective population of fine structure levels with certain ${{M}_{S}}$ values. The signs of these interactions have been determined and oscillations of the spin density on ²⁹Si and ¹³C nuclei have been found. Previously, such an effect was found for color centers with $S = 3{\text{/}}2$ in SiC [27] and was theoretically predicted for NV centers in diamond [33]. Nuclear magnetic resonance transitions at the Larmor frequencies of ¹³C and ²⁹Si and at frequencies differing from the Larmor ones by kilohertz with an oscillating spin density cause giant changes in the populations of the spin sublevels. This effect indicates a strong effect of NMR on remote nuclei on the populations of electron spin levels, changes in which can be transformed into electron spin echo and optical signals. We note that optical signals are compatible with the transparency band of fiber optics and living matter.