First Experimental Synthesis of Mg Orthocarbonate by the MgCO₃ + MgO = Mg₂CO₄ Reaction at Pressures of the Earth’s Lower Mantle

Mg-carbonate is one of the main carbonates subducting from the Earth’s surface into the mantle and possible reactions of this compound with the main mantle minerals determine the stability of carbonates into the Earth’s mantle. Recently, we have theoretically shown that at pressures and temperatures of the Earth’s lower mantle MgCO₃ should react with MgO, producing Mg₂CO₄. Here, using diamond anvil cell technique, we have performed in situ investigation of the product of MgCO₃ + MgO reaction at pressures around 50 GPa and temperatures above 2000 K. Investigation of Raman and X-ray diffraction patterns unambiguously indicates that reaction has been realized and as the reaction product we suggest the modification similar to M-g₂CO₄-$P{{2}_{1}}{\text{/}}c$. Using the transmission electron microscopy technique, we show the presence of the new Mg-orthocarbonate/carbonate phase in the sample extracted from high-pressure environment.

1 INTRODUCTION

Carbonates are the major host phases of oxidized carbon in the oceanic crust [1]. Their subduction into the Earth’s mantle is one of the main stages of the global carbon cycle, which has a major contribution to the carbon budget of the deep Earth [1–3]. According to different estimates about 20–80% of Ca, Mg, Fe-carbonates could survive decarbonation and melting beneath island arcs and be carried beyond 150 km depth to the deep mantle [1, 2]. Although they can be reduced by the redox reactions in the deep mantle to carbide and diamond [4, 5], the primary mineral inclusions of Ca- and Mg-carbonates in superdeep diamonds confirm their existence down to the lower mantle depths [6–11].

Calcite (CaCO₃) and dolomite (CaMg(CO₃)₂) are predominant phases among carbonates of the oceanic crust, however at high pressures their stability is limited by reactions with silicates, decomposition or melting processes [12, 13]. The solidus curves of carbonated peridotites and eclogites locate above the subduction geotherms at 21–32 GPa, and the occurrence of solid phases of carbonates is unlikely in the transition zone [14–20]. However, magnesite (MgCO₃) remains solid even in the case of significant melting of carbonatite in the presence of alkalis or water [17] and can be transported to the lower mantle.

Magnesite is considered as the major phase accommodating oxidized carbon in the transition zone and the upper part of the lower mantle [21]. Its structure is characterized by the triangular planar [CO₃] groups and $s{{p}^{2}}$-hybridized carbon coordinated by three oxygen atoms. Magnesite is stable up to 80–115 GPa and 2500 K in the pure carbonate system [22–25], and transforms further into the MgCO₃-II, monoclinic polymorph ($C2{\text{/}}m$) with tetrahedral [CO₄] groups and $s{{p}^{3}}$-hybridized carbon atoms. The structure of MgCO₃-II was first theoretically predicted [22] and then solved from the single crystal X-ray diffraction data for Fe-containing magnesite [26] and for pure magnesite [27].

Carbonates of M₂CO₄ and M₃CO₅ composition with tetrahedrally coordinated carbon atoms were recently found in the carbonate–oxide systems MgCO₃–MgO, CaCO₃–CaO, SrCO₃–SrO, BaCO₃–BaO [28, 29], and PbCO₃–PbO [30]. These compounds were called orthocarbonates (M₂CO₄) and oxyorthocarbonates (M₃CO₅), the salts of hypothetical orthocarbonic acid H₄CO₄. At the moment, the performed experiments have confirmed the existence of Ca₂CO₄-$Pnma$ [31], Sr₂CO₄-$Pnma$ [32], and Sr-₃CO₅-$I4{\text{/}}mcm$ [33]. In accordance with the predictions, all found structures are characterized by the covalently bonded [CO₄] groups and have isostructural analogues among silicates [28]. Some of the orthocarbonates turned out to be dynamically stable at ambient pressure, which was confirmed by their complete decompression and successful extraction from the chamber of the high-pressure cell, which was realized for Sr₂CO₄-$Pnma$ [32] and Sr₃CO₅-$Pnma$ [33].

Unlike all the previously studied carbonate–oxide systems, the MgCO₃–MgO system is the most relevant one for the Earth’s lower mantle, as both phases, ferropericlase and magnesite, could be present under mantle conditions. Based on crystal structure prediction calculations, we have recently shown that at pressures above 50 GPa and temperature of 2000 K, MgCO₃ reacts with MgO producing Mg₂CO₄ [34]. Two high-pressure phases, Mg₂CO₄-$Pnma$ stable below 80 GPa and Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ stable above this pressure, were predicted. In contrast to other alkaline earth metals, stable structures of Mg₃CO₅ were not found.

In the present work, guided by the performed predictions, we experimentally in situ investigate the products of reaction between MgCO₃ and MgO at pressures around 50 GPa as well as we perform investigation of the products extracted from the high-pressure cell.

2 EXPERIMENTAL TECHNIQUE AND DETAILS OF CALCULATIONS

2.1 Experimental Techniques

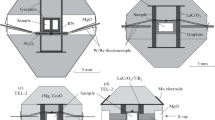
Experiments were conducted at high pressure in symmetric diamond anvil cells (DACs) with 200 μm culet size diamonds. Rhenium gaskets indented to a thickness of 30–35 μm were laser-drilled in the center of the indentation, to form a sample chamber. The  mixture of inclusion-free natural magnesite (Bahia, Brazil) with the composition of Mg_0.99Fe_0.003Ca_0.004CO₃ and analytical grade MgO (99.9%, Merck) was grinded into fine powder, carefully mixed and placed inside the sample chamber together with a small amount of Pt powder (99.9%, Alfa Aesar) as an absorber for laser heating and a pressure calibrant. Pressure was determined using the Pt equation of state [35].

All experimental runs were conducted as follows. Pressure was first increased up to the desired value at room temperature. Then samples were heated using the double-side laser-heating technique by a continuous-wave 100 W 1070 nm YLR-100-AC (IPG Photonics) Yb fiber laser with a nearly flat-top intensity distribution and beam size of nearly 10 μm in the focal plane [36]. Temperature was measured simultaneously from both sides of the diamond anvil cell (DAC) with the use of spectral radiometry; the thermal emission spectra were fitted to a grey-body Planck radiation function with T-Rax software (developed by C. Prescher).

The Raman spectra were measured before and after every heating cycle with a HORIBA Jobin Yvon LabRAM HR800 VIS spectrometer (GFZ, Potsdam) equipped with a green (532 nm) Nd : YAG laser. The software Fityk [37] was used for data analysis.

X-ray diffraction (XRD) study was performed using a focused monochromatic beam ($\lambda = 0.29{\kern 1pt}$ Å) at the extreme condition beamline P02.2 at Petra-III (DESY, Hamburg, Germany). XRD data were acquired at each pressure after heating to observe possible phase transformations. The DACs used in the first and third runs (EXP1, EXP3, see below) have a smaller opening angle, allowing only powder XRD patterns to be collected. The diffraction images were integrated using the Dioptas software to obtain one‑dimensional diffraction profiles [38]. In the se-cond set of experiments (EXP2), DAC with an opening angle of ±30° was used in order to collect s-ingle crystal XRD data. Step scans were performed with an omega increment of 0.5°. The processing of obtained data in CrysAlisPro software (including CrysAlisTabbiner routine by K. Glazyrin [https://github.com/DESY-Petra-III/CrysalisTabbiner]) was performed using E-SPERANTO protocol [https://doi.org/10.1107/S0909049513018621].

In total, three experimental runs have been performed:

—EXP1: with heating up to 3600 K at ~ 50 GPa and further measurement of powder X-ray diffraction;

—EXP2: with heating up to 2700 K at ~ 55 GPa, and further measurement of single crystal X-ray diffraction spectra;

—EXP3: with heating not exceeding 3000 K at ~55 GPa, and further measurement of powder X-ray diffraction.

After the experiments, samples were extracted from the DAC and analyzed by transmission electron microscopy (TEM) technique. The electron-transparent foils (15 × 10 × 0.15 μm) were prepared in the middle of the heated areas by the focused ion beam (FIB) method (FEI FIB 200 TEM, GFZ Potsdam) [39]. TEM was done with a Tecnai G2 F20 X-Twin transmission electron microscope operating at 200 kV with a field emission gun (FEG) as the electron source (GFZ, Potsdam). The TEM is equipped with a Gatan TridiemTM energy filter, an EDAX GenesisTM X-ray analyzer and a Fishione high angle annular dark field detector (HAADF) for electron energy-loss spectroscopy (EELS) and energy filtered imaging. Bright and dark field images as well as high-resolution images were acquired. The electronic structures of each element were investigated using EELS spectra collected at the carbon and oxygen K edges with an energy dispersion of 0.1 eV/channel. The diffraction patterns calculated by means of the fast Fourier transformation (FFT) from high-resolution images were used to measure d-spacings and angles between the adjacent lattice planes. The spectra were processed (background subtraction, removal of multiple scattering, Fourier ratio deconvolution) using the Digital Micrograph software package.

The chemical composition and homogeneity of the samples were characterized by electron microprobe analysis using JEOL Hyperprobe JXA-8500F EMP with a field emission cathode (GFZ, Potsdam). Analyzes were conducted at a 15 kV acceleration voltage, a 10 nA beam current, and a 0.5–10 μm beam size. Dolomite, calcite, and siderite with known compositions were used as standard materials.

2.2 Details of Calculations

All calculations were performed within the density functional theory (DFT) implemented in the VASP [40, 41]. The exchange-correlation interaction was taken into account in the generalized gradient approximation in the form of the Perdew–Burke–Ernzerhof (PBE) functional [42]. Core electrons were approximated using projector augmented-wave (PAW) pseudopotentials [41], and valence electrons were represented with a plane wave basis set with a cutoff energy of 800 eV. The valence configurations have been chosen as Mg ($2{{p}^{6}}3{{s}^{2}}$), C ($2{{s}^{2}}2{{p}^{2}}$), and O ($2{{s}^{2}}2{{p}^{4}}$). The Brillouin zone was sampled by a Γ-centered Monkhorst–Pack [43] k-point grid of spacing of 0.2 Å^–1.

The following crystal structures have been used: MgCO₃-$R\bar {3}c$ [44], MgO-$Fm\bar {3}m$ [45], Mg₂CO₄-Pnma [34], Mg₂CO₄-P2₁/c [34], MgO₂-$Pa\bar {3}$ [46], MgO₂-I4/mcm [46], $\epsilon$-O₂ [47], Mg₂C-$Fm\bar {3}m$ [48], Mg₂C-$Pnma$ [49], Mg₂C-$P{{4}_{2}}{\text{/}}mnm$ [48], Mg₂C-$P{{6}_{3}}{\text{/}}mmc$ [48].

To take into account the temperature effect and calculate the P–T phase diagrams, we used the lattice dynamics method within the quasi-harmonic approximation (QHA), similarly as in [50]. For this task, the lattice vibration frequencies were calculated with the PHONOPY code [51]. In order to obtain the Raman spectra, the polarizability tensors for each crystal mode were calculated using the vasp_raman.py code [52].

3 RESULTS

3.1 Raman Spectroscopy

The Raman spectra measured before and after the heating at 50 and 55 GPa are shown in Fig. 1. The spectra collected before heating contain three high intensity bands at 1225, 824, 539 cm^–1 and a low intensity broad feature at 348 cm^–1, showing the presence of magnesite [27]. High frequency bands (800–1300 cm^–1) are attributed to the internal vibrations of the [CO₃] groups: symmetric stretching (${{\nu }_{1}}$) and in-plane bending (${{\nu }_{4}}$). The magnesite symmetric stretching vibration remains a predominant feature on the Raman spectra in the high-frequency region even after heating to 3600 K. The lattice vibrations located at low frequencies (539 and 348 cm^–1) grow in intensity and become sharper with heating up to 2700 K.

Fig. 1.

(Color online) Experimental Raman spectra collected before and after heating at 50 and 55 GPa.

New bands appear in the range of 100–800 cm^–1 on Raman spectra collected at 2500 K as broad features and increase in intensity with temperature. At least three new modes could be distinguished at 2500 K: at 285, 565, and 644 cm^–1. Additionally, the shoulder appears on the low frequency side of the magnesite ${{\nu }_{4}}$ band at 825 cm^–1. High frequency region does not change up to 2700 K and displays magnesite ${{\nu }_{1}}$ mode. Further evolution of the spectra after heating at 2700 K is marked by the increasing intensity of the 565 and 644 cm^–1 bands and distinguishable new features at 250, 1040, and 1100 cm^–1. The Raman spectra collected after heating to 3600 K shows the same set of modes, however, with significantly decreased relative intensities of initial magnesite bands, and predominance of the new peaks below 900 cm^–1.

The appearance of the new bands indicates the formation of the phases, which are different from magnesite. In order to refine the spectra, all the known compounds in the system Mg–C–O were considered. The high-frequency modes at 1040 and 1100 cm^–1 could be assigned to the O–O stretching vibrations in the peroxide ion. Magnesium peroxide has two known high-pressure polymorphs with cubic ($Pa\bar {3}$) and tetragonal ($I4{\text{/}}mcm$) symmetry. For both peroxides the O–O stretching vibrations are the main characteristic features as they display the highest intensity [53]. They appear in the spectrum of the quenched sample only after heating at 2700 K. Due to the peaks overlapping it cannot be unambiguously concluded that one or another phase of peroxide appears in experiment (Fig. S1).

The bands in the low frequency region of the spectra require the presence of the additional phase, which has already been formed at 2500 K, as they cannot be fully refined by magnesite–peroxide mixture. The computed Raman spectra for the monoclinic $P{{2}_{1}}{\text{/}}c$ and orthorhombic $Pnma$ phases of Mg₂CO₄ were compared with the obtained experimental data (Fig. 2 and Fig. S1). Based on the calculated theoretical sp-ectra, the new peaks in the low frequency region could be satisfactorily explained by a combination of magnesite and Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$. The monoclinic phase M-g₂CO₄‑$P{{2}_{1}}{\text{/}}c$ shows better fit with experimental spectra than orthorhombic one Mg₂CO₄-$Pnma$. The only stable Mg-carbide at 50–55 GPa, Mg₂C-$Pnma$, was not observed in experimental spectra (Fig. S1).

Fig. 2.

(Color online) Experimentally determined Raman spectra (a, b) at 3600 K and 50 GPa and (c, d) at 55 GPa and 2700 K in comparison with DFT calculations for the Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$, MgCO₃-$R\bar {3}c$, and MgO₂-$I4{\text{/}}mcm$ phases at 60 GPa.

3.2 X-ray Diffraction

The XRD mapping obtained in EXP1 showed the appearance of a new phase with a peak near $d =$ 1.90 Å in the heating spot (Fig. S2a). Unfortunately, we could not unambiguously identify any other XRD peaks belonging to this phase neither on powder patterns, nor in single-crystal steps scans (the latter due to the small opening angle ±10° of the DAC used in these experiments). The only phase in the Mg–C–O system characterized by the intense peak at 1.9 Å is the peroxide MgO₂-$I4{\text{/}}mcm$ (Fig. 3a), the presence of which was also confirmed by Raman spectra.

Fig. 3.

(Color online) XRD powder patterns from (a) EXP1 and (b) EXP3 together with the calculated peak positions of Pt, MgO, MgO₂-$I4{\text{/}}mcm$, magnesite, Mg₂C, Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ at a pressure of ~50 GPa.

In the second attempt to reproduce formation of new phases upon laser heating in EXP3, the same mixture of (MgO + MgCO₃ + Pt) was compressed to nearly the same pressure of ~50 GPa but heated to lower temperatures, not exceeding 3000 K. The powder XRD profiles after heating showed again the appearance of peaks indicating the formation of a new phase. As such a phase we suggest Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ which show the best agreement with experimental spectra (Fig. 3b). The difference in positions and intensities of experimental diffraction peaks and peaks of the Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ is noteworthy. Based on this difference, we suggest that phase not identical but structurally similar to Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ was obtained in experiment.

In the EXP2, a DAC with a large opening angle has been used in order to collect single-crystal XRD from the grains of newly formed phases. The technique used allowed indexing of “multi-grain” data, so that single-crystal diffraction patterns were indexed for the following phases:

(1) trigonal or hexagonal phase with representative cell $a = 4.378(4){\kern 1pt}$ Å and $c = 12.67(3){\kern 1pt}$ Å, unambiguously interpreted as magnesite;

(2) cubic phase with $a = 3.741(2){\kern 1pt}$ Å unambiguously interpreted as Pt at pressure of ~55 GPa;

(3) unknown trigonal or hexagonal phase with representative cell $a = 2.693(4){\kern 1pt}$ Å and $c = 6.517(12){\kern 1pt}$ Å.

Unfortunately, the quality of the diffraction pattern of the unknown phase has not allowed us to solve its crystal structure. The unit cell of this phase does not produce reflections close to those observed in powder XRD patterns of EXP1 and EXP3 and we have not found any phases in the Mg–C–O system with similar cell parameters.

3.3 Transmission Electron Microscopy

The perpendicular cross-section of the laser heated spot was prepared for the TEM analysis to obtain the textures, spatial relationships, and semi-quantitative chemical compositions of the solid phases. The thin films were prepared from the spot annealed at 50 GPa up to 3600 K. The TEM image shows a multiphase assemblage in the heated area (Fig. S2b). A large void in the center of the sample in Fig. S2 reflects the presence of the fluid phase at high pressures and temperatures that was released during the decompression process. The phase assemblages change from the center of the heated spot and form distinct zones that appear due to the temperature gradient within the heated spot. The sample consists of the following phases: untransformed magnesite and Mg-oxide in the outer rim, new Mg-carbonate/orthocarbonate in the middle, and platinum with relicts of oxide closer to the center. The EDS spectrum of the new Mg-carbonate/orthocarbonate is shown in Fig. S2c.

Three HRTEM images and corresponding electron diffraction patterns of the new carbonate/orthocarbonate phase have been obtained. The diffraction patterns cannot be indexed with the magnesite structure. Both phases of orthocarbonate, Mg₂CO₄-$Pnma$ with unit cell parameters $a = 9.94{\kern 1pt}$ Å, $b = 5.96{\kern 1pt}$ Å, $c =$ 4.46 Å and Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ with unit cell parameters $a = 5.172{\kern 1pt}$ Å, $b = 6.174{\kern 1pt}$ Å, $c = 9.2780{\kern 1pt}$ Å, and $\beta = 120.486^\circ$, show acceptable fit of the obtained diffraction spectra. The deviation of the experimentally measured d-spacings does not exceed 0.08 Å with the average value of 0.03 Å and deviation of the angles between hkl-planes is within two degrees (Fig. 4).

Fig. 4.

(a) Micrographs (TEM bright-field), (b) HRTEM image, and (c) diffraction pattern (FFT) obtained for the new phase; hkl indices are given according to the Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ structure. The HRTEM image and electron diffraction pattern were obtained from the region inside the white circle.

The EELS spectra of the Mg-carbonate from the C K edge (Fig. 5) show a shift of the main peak of the new carbonate to 292.7 eV, while magnesite peak locates at 290.5 eV. The obtained spectra from the O K edges of the new carbonate phase are as well different from that of magnesite with the main peaks observed at the 1–2 eV higher positions.

Fig. 5.

(Color online) O and C K edges of (blue curve) Mg₂CO₄ and (red curve) reference MgCO₃.

4 DISCUSSION AND CONCLUSIONS

Both Raman and X-ray diffraction experiments unambiguously shown formation of the new phase as the result of reaction between MgCO₃ and MgO at pressures around 50 GPa. The only phase in the Mg‒C–O system which does not contradict to the obtained spectra is Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$. In Supplementary materials, it is shown that high-pressure phases of O₂, CO₂ or Mg-carbides are not consistent with the obtained results. We also exclude the possibility for the reaction between initial reagents (MgCO₃ and MgO) and platinum, as numerous earlier performed experiments with this compounds in which Pt was used as heat absorber have not found any signs of their interaction [24, 54].

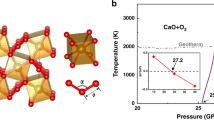
Earlier [34], based on the theoretical predictions we have shown stability at high pressures and temperatures of two orthocarbonate phases Mg₂CO₄-$Pnma$ and Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ (Fig. 6a). Here, we reanalyzed energetic relationships between phases and find out that the only thermodynamically stable phase of M-g₂CO₄ is $P{{2}_{1}}{\text{/}}c$. Mg₂CO₄-$Pnma$ phase is metastable in the whole P–T range, at least within quasi-harmonic approximation (Fig. 6b). This is consistent with  the results of the experiments, showing better co-rrespondence for Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ phase than for M-g₂CO₄-$Pnma$. Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ according to theoretical calculations became stable starting from the pressure of 70 GPa. This is 20 GPa higher than the pressure of appearance of Mg-orthocarbonate in our experiments. The difference in pressures can be attributed to the inherent difference of theoretical model and real experiment and also to the structural difference between the phase observed in experiment and Mg-₂CO₄-$P{{2}_{1}}{\text{/}}c$. If the phase more energetically favorable than Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ was realized in e-xperiment, hence the lower pressure limit of its th-ermodynamic stability will be lower than that of Mg-₂CO₄‑$P{{2}_{1}}{\text{/}}c$.

Fig. 6.

(Color online) (a) P–T phase diagram presented in [34] and (b) the corrected P–T phase diagram of Mg₂CO₄ according to new data; the orange star shows the approximate (P, T) parameters at which the experiments were performed, the gray solid line is the mantle adiabat, the gray dashed line is the melting curve of magnesite (MgCO₃-$R\bar {3}c$), and the gray dash-dotted line is the MgCO₃-$R\bar {3}c$ $\to$ MgCO₃-$C2{\text{/}}m$ phase transition boundary.

The obtained TEM results suggest stability of the synthesized Mg-orthocarbonate at ambient pressure. According to theoretical calculations Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ is dynamically stable at ambient pressure as well. However, the phase obtained in experiment is not identical to Mg₂CO₄-$P{{2}_{1}}{\text{/}}c$ and its dynamic stability at ambient pressure is unclear.

The found appearance of Mg-peroxide in our experiments deserves attention. We suggest that it was produced by the reaction which is typical of other MCO₃–MO systems with alkaline earth metals. At least in our unpublished experiments, we observed formation of SrO₂ at heating of (SrCO₃ + SrO) mixture. The calculated values of Gibbs free energies indicated that MgO₂ is metastable in our experiments and it should decompose on the mixture of (MgO + 0.5O₂) at pressures below 100 GPa (Fig. S4). However, the metastable formation of Mg-peroxide is not unusual, as its ambient pressure synthesis is realized in industrial scale. The reaction by which MgO₂ was formed in our experiments is unclear, it can be suggested that it is one of the decomposition products of Mg-orthocarbonate.

The found complex phase behavior of the MgCO₃–MgO system at high pressures and temperatures and the possible existence of the phases, which were not described in any previous experiments, expand the list of carbon-host phases taking part in the global carbon cycle. It was previously believed that magnesite will be the main carbon carrier at the P–T conditions of the Earth’s lower mantle, and will transform to MgCO₃-II with tetrahedral coordination of carbon at pressures higher than 80 GPa. However, as demonstrated in the present study it’s reaction with periclase implies that magnesium orthocarbonates with tetrahedrally coordinated carbon can form at sufficiently lower pressures, around 50 GPa.