Spin Navigator Based on Correcting Dipoles of the JINR Nuclotron

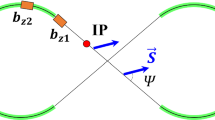
A spin navigator based on correcting dipoles has been proposed to manipulate the directions of protons spins in experiments at the Nuclotron synchrotron (JINR, Dubna). The polarization is controlled by means of the controllable distortion of the beam closed orbit by correcting dipoles, which ensures the significant enhancement of the action of the navigator on the spins of particles. A method has been proposed to measure the coherent effect of the lattice imperfection on the spin dynamics by the navigator. An idea of a spin compensator based on correcting dipoles is presented, which allows one to eliminate the effect of the lattice imperfection on the polarization. The proposed navigator and spin compensator make it possible to perform a series of experiments at the Nuclotron to verify a new polarization control technique called the spin transparency mode. The results are relevant for experiments with polarized beams in the spin transparency regime at the NICA (Dubna, Russia) and EIC (Brookhaven, United States) and the COSY synchrotron (Julich, Germany).

INTRODUCTION

For studies with polarized proton and deuteron beams at the NICA (JINR, Dubna) [1–4], it is planned to use a new polarization control technique called the spin transparency mode (ST mode) [5, 6]. In this mode, the action of structural magnets on the spin is completely compensated, when the particle is on the design orbit: any spin direction is repeated in each turn of the particle. This means that particles are in the spin resonance region (ST resonance). To ensure the ST mode in a continuous range of beam energies, two solenoid Siberian snakes are placed in the opposite straight sections of the NICA [7]. The polarization of the beam in the ST mode is controlled by spin navigators using low magnetic fields, which allow one to stabilize any direction of the polarization during experiments [8].

The experimental verification of the ST mode at the JINR is planned at the Nuclotron synchrotron [9, 10], which is an injector of polarized protons and deuterons to the NICA. The ST mode in the Nuclotron can be ensured without solenoid snakes at discrete energies corresponding to integer spin resonances [10]

$$\nu = \gamma G = k,\quad k = 1,2, \ldots {\kern 1pt} ,$$

(1)

where ν is the spin tune in units of the particle revolution frequency (the spin tune), G is the anomalous part of the gyromagnetic ratio, and γ is the relativistic factor.

The polarization of the beam accelerated to the energy of the experiment should be kept. Depolarization is mainly due to the crossing of linear-approximation spin resonances, the strongest of which are integer spin resonances caused by the manufacture and misalignments errors of magnetic elements of the synchrotron, as well as intrinsic resonances caused by betatron oscillations of the beam.

The possibility of experimentally testing the ST mode for protons with momenta up to 3 GeV/c, where intrinsic resonances of the Nuclotron are absent, using two weak solenoids was analyzed in [11]. Navigator solenoids with a field integral of about 0.3 T m ensure not only the control of the polarization of protons but also the adiabatic crossing of integer resonances with the polarization kept in the process of acceleration of the beam [12].

In this work, we propose a spin navigator that is based on correcting dipoles existing in the magnetic lattice of the Nuclotron and does not require additional magnetic fields.

SPIN NAVIGATOR BASED ON LOW TRANSVERSE FIELDS

A method for the calculation of spin navigators using spin response functions [13–16] is presented in [17]. Correcting dipoles with the radial, ${{b}_{x}}$, and vertical, ${{b}_{y}}$, magnetic fields induce the spin navigator field ${{{\mathbf{h}}}_{{{\text{nav}}}}}$. The spin of a particle directed along the navigator field will repeat its direction in each turn of the particle moving in the closed orbit. The spin of the particle perpendicular to the navigator field in each turn is rotated about the navigator field by a small angle $2\pi {{\nu }_{{{\text{nav}}}}}$, which determines the navigator tune ${{\nu }_{{{\text{nav}}}}} = {\text{|}}{{{\mathbf{h}}}_{{{\text{nav}}}}}{\text{|}}$. The navigator field is a periodic function of the z coordinate along the closed orbit

$${{{\mathbf{h}}}_{{{\text{nav}}}}}(z) = {{{\mathbf{h}}}_{{{\text{nav}}}}}(z + L){\kern 1pt} ,$$

(2)

where L is the length of the design orbit.

The spins of particles directed along the axis n of the navigator will undergo stable periodic motion, whereas the spins of particles perpendicular to the axis of the navigator will be smeared because of the spread of the navigator tune and tunes of orbit motion.

The components of the navigator field are constant in the spin coordinate system [18], whose unit vectors ${{{\mathbf{s}}}_{i}}$ describe the real dynamics of spins in the process of motion of the particle on the design orbit:

$$\begin{gathered} {{{\mathbf{h}}}_{{{\text{nav}}}}} = \sum\limits_{i = 1}^3 {{h}_{{{\text{nav}},i}}}{\kern 1pt} {{{\mathbf{s}}}_{i}},\quad {{h}_{{{\text{nav}},i}}} = ({{{\mathbf{h}}}_{{{\text{nav}}}}} \cdot {{{\mathbf{s}}}_{i}}), \\ {{h}_{{{\text{nav}},i}}} = \frac{1}{{2\pi }}\int\limits_0^L \left( {\frac{{{{b}_{x}}}}{{B\rho }}{{F}_{{xi}}} + \frac{{{{b}_{y}}}}{{B\rho }}{{F}_{{yi}}}} \right)dz, \\ \end{gathered} $$

(3)

where $B\rho$ is the magnetic rigidity and ${{F}_{{xi}}} = ({{{\mathbf{F}}}_{x}} \cdot {{{\mathbf{s}}}_{i}})$ and ${{F}_{{yi}}} = ({{{\mathbf{F}}}_{y}} \cdot {{{\mathbf{s}}}_{i}})$ are the components of the response function along the radial and vertical directions, respectively.

The components of the vertical response function for the Nuclotron, which is an eight-superperiod synchrotron with a vertical guiding field are zero: ${{F}_{{yi}}} = 0$. Consequently, only the radial magnetic fields ${{b}_{x}}$ contribute to the navigator field. In the accelerator system of unit vectors $({{{\mathbf{e}}}_{x}},{{{\mathbf{e}}}_{y}},{{{\mathbf{e}}}_{z}})$ related to the velocity of the particle, the spin unit vector ${{{\mathbf{s}}}_{2}}$ is constant and is directed along the vertical, and spin unit vectors ${{{\mathbf{s}}}_{1}}$ and ${{{\mathbf{s}}}_{3}}$ are rotated about the vertical direction ${{{\mathbf{e}}}_{y}}$ in arc dipoles

$$\begin{gathered} {{{\mathbf{s}}}_{2}} = {{{\mathbf{e}}}_{y}}, \\ {{{\mathbf{s}}}_{1}} + i{\kern 1pt} {{{\mathbf{s}}}_{3}} = ({{{\mathbf{e}}}_{x}} + i{\kern 1pt} {{{\mathbf{e}}}_{z}})\exp \left( {i{\kern 1pt} \gamma G\int\limits_0^z \frac{{{{B}_{y}}}}{{B\rho }}dz} \right). \\ \end{gathered} $$

(4)

A correcting dipole with the radial field distorts the closed orbit in the vertical plane of the Nuclotron. As a result, the spins of particles are subjected not only to the direct action of the dipole magnetic field but also to the additional action of magnetic fields generated upon the motion of the particle along this distorted orbit. The partial contribution to the navigator field ${{{\mathbf{h}}}_{i}} = {{\nu }_{i}}{\kern 1pt} {{{\mathbf{n}}}_{i}}$ from a short correcting dipole with the length ${{L}_{i}}$ and the radial field ${{b}_{{x,i}}}$ that is located at a point with the coordinate ${{z}_{i}}$ is determined by the response function

$$\begin{gathered} {{\nu }_{i}} = \frac{{{\text{|}}{{{\mathbf{F}}}_{x}}({{z}_{i}}){\text{|}}}}{{2\pi }}\frac{{{{b}_{{x,i}}}{\kern 1pt} {{L}_{i}}}}{{B\rho }} = \frac{{{{\varphi }_{{x,i}}}}}{{2\pi }}{{k}_{x}}({{z}_{i}}), \\ {{{\mathbf{n}}}_{i}}(z) = \sum\limits_{j = 1}^3 \frac{{{{F}_{{xj}}}({{z}_{i}})}}{{{\text{|}}{{{\mathbf{F}}}_{x}}({{z}_{i}}){\text{|}}}}{{{\mathbf{s}}}_{j}}(z), \\ \end{gathered} $$

(5)

where ${{\varphi }_{{x,i}}} = \gamma G{{\alpha }_{{{\text{orb}}}}}$ is the spin rotation angle, α_orb is the rotation angle of the orbit by the correcting dipole, and

$${{k}_{x}}(z) = \frac{{{\text{|}}{{{\mathbf{F}}}_{x}}(z){\text{|}}}}{{\gamma G}}$$

(6)

is the navigator tune enhancement factor ${{k}_{x}}$ caused by the distortion of the closed orbit.

Figure 1 shows the dependences of the enhancement factor ${{k}_{x}}$ for protons on the z coordinate in one superperiod of the Nuclotron for the $\gamma G = k$ ST resonances in the momentum range up to 3 GeV/c. The enhancement factor for resonances with numbers 2, 3, and 4 is ${{k}_{x}} < 1$ at any point of the orbit; i.e., the optical structure of the Nuclotron will partially compensate the direct action of correcting dipoles on the spin. The enhancement factor for resonance no. 5 is ${{k}_{x}} \sim 1$; i.e., the optical structure hardly provides an additional action on spins compared to the direct action of correcting dipoles. The enhancement factor for resonance no. 6 is ${{k}_{x}} > 1$; i.e., the optical structure will enhance the direct action of correcting dipoles by a factor of 2–3.

Fig. 1.

(Color online) Enhancement coefficients of the navigator tune ${{k}_{x}}$ versus the z coordinates for spin transparency resonances $\gamma G = k$ ($k = 2,3,4,5,6$) in one superperiod of the Nuclotron.

In the linear approximation in low navigator fields ${{b}_{{x,i}}}$ (partial navigator tunes ${{\nu }_{i}}$), the total navigator field produced by N_dip correcting dipoles is the sum of the partial fields:

$${{{\mathbf{h}}}_{{{\text{nav}}}}}(z) = \sum\limits_{i = 1}^{{{N}_{{{\text{dip}}}}}} {{{\mathbf{h}}}_{i}}(z) = \sum\limits_{i = 1}^{{{N}_{{{\text{dip}}}}}} {{\nu }_{i}}{\kern 1pt} {{{\mathbf{n}}}_{i}}(z).$$

(7)

To stabilize spin motion, the action of the navigator on the spin should significantly exceed the action of perturbing magnetic fields caused by the manufacture and misalignments errors of magnetic elements of the Nuclotron and by betatron oscillations; i.e., the navigator tune should be much higher than the ST resonance strength [5]

$${{\nu }_{{{\text{nav}}}}} \gg \omega {\kern 1pt} {\kern 1pt} .$$

(8)

EFFECT OF SYNCHROTRON OSCILLATIONS IN THE SPIN TRANSPARENCY MODE AT INTEGER RESONANCES

The spin tune in the ST mode at integer resonances is proportional to the energy; as a result, additional constraints are imposed on the fields of spin navigators because of synchrotron oscillations, which split an ST resonance into a series of satellite resonances [10, 11]. In the presence of synchrotron oscillations, the spins of particles are rotated about the field

$${\mathbf{h}} = {{{\mathbf{h}}}_{{{\text{nav}}}}} + {{\varepsilon }_{{{\text{rf}}}}}{{{\mathbf{e}}}_{y}}.$$

(9)

Here, ε_rf serves as detuning from the ST resonance along the vertical direction and is given by the formula

$${{\varepsilon }_{{{\text{rf}}}}} = \sigma {\text{cos}}{{\Psi }_{\gamma }}.$$

(10)

Here, $\sigma = G\Delta \gamma$ is the amplitude of the synchrotron modulation of the spin tune and Ψ_γ = 2πν_γz/L + Ψ₀, where ν_γ and Ψ₀ are the tune and initial phase of synchrotron oscillations, respectively. Satellite resonances appear under the condition

$${{h}_{m}} = \sqrt {\nu _{{{\text{nav}}}}^{2} + \varepsilon _{{{\text{rf}}}}^{2}} = m{{\nu }_{\gamma }},\quad m = \pm 1, \pm 2, \ldots .$$

(11)

The spin dynamics significantly depends on the navigator tune ν_nav and on the rate of crossing of the central resonance σν_γ [19]. In the case of fast crossing ($\nu _{{{\text{nav}}}}^{2} \ll \sigma {{\nu }_{\gamma }}$), synchrotron oscillations result in the crossing of σ/ν_γ satellite resonances; the strengths of these and central resonances is reduced by a factor of J_m(σ/ν_γ). It is noteworthy that the direction of the spin field (9) under the condition ${{\nu }_{{{\text{nav}}}}} \ll \sigma$ will significantly deviate from the axis of the navigator with increasing of the detuning from the central resonance.

In another limiting case $\nu _{{{\text{nav}}}}^{2} \gg \sigma {{\nu }_{\gamma }}$, the navigator can adiabatically capture spins. In this case, condi-tion (11) at

$${{\nu }_{{{\text{nav}}}}} \gg \max ({{\nu }_{\gamma }},\sigma )$$

(12)

is valid only for satellite resonances with large numbers whose strengths decrease sharply with an increase in the number of resonance. In this case, the direction of the spin field (9) insignificantly deviates from the axis of the navigator.

STRENGTH OF THE SPIN TRANSPARENCY RESONANCE IN THE NUCLOTRON

The depolarizing effect of the Nuclotron lattice imperfection on the polarization of protons was analyzed in [10] with spin response functions for the ST mode at integer resonances in the momentum range up to 3 GeV/c.

The strength of the ST resonance is determined by the field of the ST resonance ω, which is due to the deviation of the particle trajectory from the design orbit because of manufacture and misalignments errors of the Nuclotron lattice and of the beam emittances. In the absence of navigator fields, the spin is rotated about the ω direction by an angle of 2πω per turn of the particle. The field of the ST resonance is the sum of two components

$${\boldsymbol{\omega }} = {{{\boldsymbol{\omega }}}_{{{\text{coh}}}}} + {{{\boldsymbol{\omega }}}_{{{\text{emit}}}}},$$

(13)

where ω_coh is the coherent component caused by additional transverse and longitudinal fields in a trajectory deviating from the design orbit and ω_emit is the incoherent component associated with the beam emittances of betatron and synchrotron oscillations.

The perturbation of the radial field $\Delta {{B}_{x}}$ in the Nuclotron can be due to random shifts of quadrupoles in the vertical direction $\Delta {{y}_{q}}$ and rotations of magnets $\Delta {{\alpha }_{z}}$ about the longitudinal direction. The perturbation of the longitudinal field $\Delta {{B}_{z}}$ is caused by random rotations of magnets $\Delta {{\alpha }_{x}}$ about the radial direction. The incoherent component of the spin field ω_emit caused by betatron oscillations is nonzero only in the second order of the amplitudes of oscillations of the particles and is proportional to the betatron emittances of the beam. The incoherent component of the power was calculated with the spin-tracking code Zgoubi [20]. Table 1 presents the coherent, ω_coh, and incoherent, ω_emit, parts of the ST resonance strength for integer spin resonances calculated with the parameters $\Delta {{y}_{q}}$ ~ 0.1 mm, $\Delta {{\alpha }_{z}}$ ~ 0.1 mrad, $\Delta {{\alpha }_{z}}$ ~ 0.3 mrad, and a value of 4.5π mm mrad for the normalized betatron emittances in the vertical and radial directions.

Table 1. Strengths of integer spin resonances in the Nuclotron

SPIN NAVIGATOR IN THE NUCLOTRON

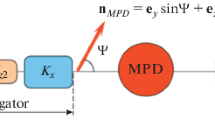
The vertical component of the radial response function in the Nuclotron is absent: ${{F}_{{x2}}} = 0$. This means that the partial navigator fields lie in the plane of the Nuclotron and each such field can be characterized by two parameters: the navigator tune enhancement factor ${{k}_{{x,i}}}$ and the angle ${{\alpha }_{i}}$ between the directions of the velocity and the n_i partial axis:

$${{\nu }_{i}} = \frac{{{{\varphi }_{{x,i}}}}}{{2\pi }}{{k}_{{x,i}}},\quad {{{\mathbf{n}}}_{i}} = (\sin {{\alpha }_{i}},{\kern 1pt} 0,{\kern 1pt} \cos {{\alpha }_{i}}).$$

(14)

Thus, two correcting dipoles are sufficient to obtain any required direction of the resulting axis of the navigator and navigator tune. The integrals of the radial fields of these correctors are calculated by the formulas

$$\begin{gathered} {{b}_{{x,1}}}{{L}_{1}} = \frac{{2\pi {{\nu }_{{{\text{nav}}}}}}}{{\gamma G{{k}_{{x,1}}}}}\frac{{\sin (\alpha - {{\alpha }_{2}})}}{{\sin ({{\alpha }_{1}} - {{\alpha }_{2}})}}{\kern 1pt} B\rho , \\ {{b}_{{x,2}}}{{L}_{2}} = \frac{{2\pi {{\nu }_{{{\text{nav}}}}}}}{{\gamma G{{k}_{{x,2}}}}}\frac{{\sin (\alpha - {{\alpha }_{1}})}}{{\sin ({{\alpha }_{2}} - {{\alpha }_{1}})}}{\kern 1pt} B\rho {\kern 1pt} , \\ \end{gathered} $$

(15)

where α is the angle between the net axis of the navigator and the velocity direction. According to these formulas, dipoles with partial navigator axes perpendicular to each other are preferable; in this case, ${\text{|}}\sin ({{\alpha }_{2}} - {{\alpha }_{1}}){\text{|}} = 1$.

We now demonstrate how the spin navigator can be implemented with correcting dipoles in the Nuclotron by the example of the $\gamma G = 6$ ST resonance. Let the origin of the coordinate system be placed at the point of observation of the polarization (polarimeter, injection channel or the point of beam extraction from the Nuclotron, etc.).

Figures 2 and 3 show the enhancement factors ${{k}_{{x,i}}}$ and angles ${{\alpha }_{i}}$ for this resonance. The positions of 28 correcting dipoles in the Nuclotron are marked by triangles. A maximum enhancement factor of about 3.6 is achieved near defocusing quadrupoles in empty spaces of the superperiods of the Nuclotron. The first and fifth correcting dipoles whose axes are almost perpendicular to each other (${{\alpha }_{1}} \approx - \pi {\text{/}}2$ and ${{\alpha }_{5}} \approx \pi$) can be chosen to control the polarization of protons. In this spin navigator, the first and fifth dipoles are responsible for the radial and longitudinal polarizations at the origin of the coordinate system.

Fig. 2.

(Color online) Enhancement coefficients of the proton navigator tune ${{k}_{x}}$ of correcting dipoles of the Nuclotron for the $\gamma G = 6$ spin transparency resonance.

Fig. 3.

(Color online) Angles of deviation of the partial axes of the navigator field of correcting dipoles from the longitudinal direction in the Nuclotron for the $\gamma G = 6$ spin transparency resonance.

The maximum navigator tune is limited by the aperture of the magnetic elements of the Nuclotron. Figure 4 shows the plots of the deviation of the closed orbit upon the stabilization of the (solid line) radial and (dashed line) longitudinal polarizations at  the origin of the coordinate system by the spin na-vigator with the tune ν_nav = 2 × 10^–3. To ensure this navigator tune, the integral of the radial field in the correcting dipole should be approximately 6 mT m. The maximum deviation of the closed orbit from the design one does not exceed 15 mm in both cases.

Fig. 4.

(Color online) Deviation of the closed orbit upon the stabilization of the (solid line) radial and (dashed line) longitudinal polarizations by the spin navigator.

The aperture restrictions weaken with increasing energy. Correcting dipoles can induce the navigator tune ν_nav ≈ 10^–2 at the maximum deviation of the closed orbit of 15 mm already for the $\gamma G = 7$ resonance.

COMPENSATION OF THE SPIN TRANSPARENCY RESONANCE STRENGTH

In reality, the spin is rotated in the field ω_tot, which is the sum of the fields of the navigator and ST resonance:

$${{{\boldsymbol{\omega }}}_{{{\text{tot}}}}} = {{\nu }_{{{\text{nav}}}}}{\mathbf{n}} + {\boldsymbol{\omega }}.$$

(16)

The spins of particles directed along the navigator field will be rotated inside the cone about its axis:

$${{{\mathbf{n}}}_{{{\text{tot}}}}} = \frac{{{\boldsymbol{\omega }_{{{\text{tot}}}}}}}{{{\text{|}}{\boldsymbol{\omega }_{{{\text{tot}}}}}{\text{|}}}} \approx {\mathbf{n}} + \frac{{{\boldsymbol{\omega }_{ \bot }}}}{{{{\nu }_{{{\text{nav}}}}}}},\quad {\boldsymbol{\omega }_{ \bot }} = \boldsymbol{\omega } - (\boldsymbol{\omega } \cdot {\mathbf{n}}){\mathbf{n}}.$$

(17)

A small opening angle ψ of the polarization cone is determined by the field component of the ST resonance ${{\omega }_{ \bot }}$ perpendicular to the n axis (see Fig. 5):

$$\psi \approx {{\omega }_{ \bot }}{\text{/}}{{\nu }_{{{\text{nav}}}}}.$$

(18)

Fig. 5.

(Color online) Dynamics of the spin in the presence of the navigator and spin transparency resonance field.

The coherent component of the ST resonance field can be compensated by weak static magnetic fields (spin compensator). In this case, the opening angle of the polarization cone is minimal and is determined only by the incoherent component of the ST resonance field.

After averaging over the spins of the ensemble of particles, the polarization vector P will be directed along the n_tot axis. The degree of polarization P is determined by the average projection of spins on this axis. The degree of polarization of a completely polarized beam (all spins are directed along the n_tot axis) is P_max = ±1. The components of the field ω_coh can be determined by analyzing the measured projections of the polarization vector. The coherent field component ω_coh = (ω_x, 0, ω_z) in the Nuclotron lies in the (x, z) plane of the orbit and its components ω_x and ω_z can be measured using various methods.

In particular, the radial component ω_x can be determined by measuring successively the radial polarization components $P_{{x + }}^{{(x)}}$ and $P_{{x - }}^{{(x)}}$ when the navigator stabilizes the oppositely directed longitudinal axes ${{{\mathbf{n}}}_{{z + }}} = + {{{\mathbf{e}}}_{z}}$ and ${{{\mathbf{n}}}_{{z - }}} = - {{{\mathbf{e}}}_{z}}$ in the detector, respectively:

$$\begin{gathered} P_{{x + }}^{{(x)}} = P\sin {{\alpha }_{ + }},\quad P_{{x - }}^{{(x)}} = P\sin {{\alpha }_{ - }}, \\ {{\omega }_{x}} = \frac{{2\tan {{\alpha }_{ + }}\tan {{\alpha }_{ - }}}}{{\tan {{\alpha }_{ + }} + \tan {{\alpha }_{ - }}}}{{\nu }_{{{\text{nav}}}}}. \\ \end{gathered} $$

(19)

Here, ${{\alpha }_{ + }}$ and ${{\alpha }_{ - }}$ are the angles between the axes of the navigator ${{{\mathbf{n}}}_{{z + }}}$ and ${{{\mathbf{n}}}_{{z - }}}$ and the axis of the polarization cone n_tot, respectively. The rotation of the axis of the navigator from the ${{{\mathbf{n}}}_{{z + }}}$ direction to the ${{{\mathbf{n}}}_{{z - }}}$ direction should be performed adiabatically. In this case, the resonant depolarization of the beam is excluded if the navigator tune is maintained constant during the rotation of the axis of the navigator [10].

The longitudinal component ω_z can be similarly determined by measuring successively the radial polarization components $P_{{x + }}^{{(z)}}$ and $P_{{x - }}^{{(z)}}$ when the navigator stabilizes the oppositely directed radial axes ${{{\mathbf{n}}}_{{x + }}} = + {{{\mathbf{e}}}_{x}}$ and ${{{\mathbf{n}}}_{{x - }}} = - {{{\mathbf{e}}}_{x}}$ in the detector, respectively:

$$\begin{gathered} P_{{x + }}^{{(z)}} = P\cos {{\beta }_{ + }},\quad P_{{x - }}^{{(z)}} = P\cos {{\beta }_{ - }}, \\ {{\omega }_{x}} = \frac{{2\tan {{\beta }_{ + }}\tan {{\beta }_{ - }}}}{{\tan {{\beta }_{ + }} + \tan {{\beta }_{ - }}}}{{\nu }_{{{\text{nav}}}}}, \\ \end{gathered} $$

(20)

where ${{\beta }_{ + }}$ and ${{\beta }_{ - }}$ are the angles between the axes of the navigator ${{{\mathbf{n}}}_{{x + }}}$ and ${{{\mathbf{n}}}_{{x - }}}$ and the axis of the polarization cone n_tot, respectively.

After the determination of ${{\omega }_{x}}$ and ${{\omega }_{z}}$, the coherent field component of the ST resonance can be compensated using correcting dipoles of the Nuclotron. The spin compensator is a spin navigator with the navigator tune ν_comp and axis n_comp:

$${{\nu }_{{{\text{comp}}}}} = {{\omega }_{{{\text{coh}}}}},\quad {{{\mathbf{n}}}_{{{\text{comp}}}}} = {{{\boldsymbol{\omega }}}_{{{\text{coh}}}}}{\text{/}}{{\omega }_{{{\text{coh}}}}}.$$

(21)

SIMULATION OF THE SPIN DYNAMICS IN SPIN TRANSPARENCY RESONANCE

The spin dynamics in the region of the $\gamma G = 6$ ST resonance for the Nuclotron with the navigator was numerically simulated using the Zgoubi spin-tracking code [20].

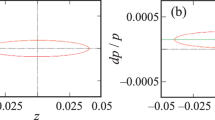
Figure 6 shows the dependence of the radial spin component ${{S}_{x}}$ on the number of rotations of the proton N upon the stabilization of the radial polarization by the navigator with the tune ν_nav = 2 × 10^–3 (dashed line) without and (solid line) with the compensation of the coherent strength of the resonance. The spin compensator was implemented with the 9th and 13th correcting dipoles, which compensated the radial and longitudinal field components of the ST resonance to a level of 10^–4 corresponding to the incoherent part of the ST resonance strength.

Fig. 6.

Stabilization of the radial polarization by the spin navigator at the Nuclotron.

According to the calculations, the opening angle of the polarization cone (18) without the compensation of the strength ω_coh is $\psi \approx 0.5$ and the spin projection S_x significantly deviates from a value of +1. After the compensation of the strength ω_coh, the opening angle becomes $\psi \approx 0.05$ and the spin projection S_x slightly deviates from its initial position. A small deviation of the radial spin projection from a value of +1 is due to the betatron motion of the beam (incoherent field component of the ST resonance).

Similar dependences of the longitudinal spin component S_z on the number of proton rotations in the case where the spin navigator stabilizes the longitudinal polarization are shown in Fig. 7.

Fig. 7.

Stabilization of the longitudinal polarization by the spin navigator at the Nuclotron.

Figure 8 presents the calculations of the adiabatic capture of the polarization by the navigator taking into account synchrotron oscillations. The calculations were carried out with the parameters ν_nav = 2 × 10^–3 and ν_γ = 2.5 × 10^–4. The thick solid line corresponds to zero momentum spread (σ = 0). The thin solid line is plotted for the case σ = 1.5 × 10^–3, where the adiabatic capture condition (12) is not satisfied: ν_nav ~ σ. In this case, the spin significantly deviates from the stabilized radial direction. The dashed line corresponds to σ = 3 × 10^–4, at which the adiabatic capture condition (12) is satisfied and the maximum deviation of the spin from the radial direction is no more than σ/ν_nav ~ 0.1 rad.

Fig. 8.

Stabilization of the radial polarization by the spin navigator taking into account synchrotron oscillations.

In the given example, the acceptable energy spread that allows the adiabatic capture of proton spins is determined by the navigator tune and is Δγ/γ ≈ 5 × 10^‒5. It can be increased by increasing the navigator tune, e.g., through an increase in the allowed transverse deviations of the closed orbit from the design one or through the optimization of the fields of existing correcting dipoles. The calculations show that the simultaneous use of the 1st, 5th, 9th, 13th, and 20th correcting dipoles with optimization at the maximum deviation of the closed orbit of 15 mm can provide a navigator tune of ν_nav = 5 × 10^–3, which makes it po-ssible to increase the acceptable energy spread to Δγ/γ ~ 10^–4.

CONCLUSIONS

A spin navigator based on existing correcting dipoles has been proposed to control the polarization of protons in the plane of the Nuclotron ring in the spin transparency mode at integer resonances. An idea of the navigator is based on the interference enhancement of the action of correcting dipoles on the spin owing to the appearance of additional fields in the perturbed closed orbit. The navigator tune at low energies is limited by the aperture of the chamber of the synchrotron. This limit is removed with increasing energy. Unlike longitudinal fields, the required integrals of dipole navigator fields do not increase with the energy at a fixed navigator tune. The proposed navigator will allow the experimental verification of a new polarization control technique called the spin transparency mode at the NICA (Dubna, Russia).

An idea of the compensation of the coherent part of the strength of the spin transparency resonance, which is due to the Nuclotron lattice imperfection, by a spin compensator based on correcting dipoles has been proposed. The compensation of the lattice imperfection allows one to minimize the opening angle of the polarization cone, which will be determined only by orbital emittances of the beam, thus finally ensuring a new accuracy level of experiments with polarized p-rotons.

The proposed spin navigator is relevant to control the polarization of deuterons in the spin transparency regime at integer resonances at the EIC (Brookhaven, United States) [21], as well as to control the polarization of protons at the NICA (Dubna, Russia) [7] and the COSY synchrotron (Julich, Germany) [22].