Exotic particles called enions whose quantum statistics is neither boson nor fermion can exist in two-dimensional electron systems (2DESs) [1, 2]. For example, it was predicted that elementary excitations of 2DESs in the regime of the fractional quantum Hall effect at a filling factor of \(\nu = 1{\text{/}}m\) (where m is an odd integer) satisfy Abelian fractional statistics with the phase ϕ = \(\pi {\text{/}}m\) related to the two-particle exchange [3, 4]. The only system where the enion statistics of particles has been already observed experimentally is the state of the fractional quantum Hall effect at a filling factor of \(\nu = 1{\text{/}}3\) [5, 6]. It is noteworthy that fractional statistics was observed in transport experiments, whereas quasiparticles in the bulk of 2DESs, for which nontrivial statistical properties were predicted, do not contribute to the conductivity. Consequently, the study of the relation between transport characteristics of fractional edge states and quasiparticles in the bulk of 2DESs is a separate nontrivial problem [7, 8]. The existing representations on neutral excitations directly in the bulk of an enion system that are inactive in transport experiments are even more limited. Pioneering studies [9, 10] of microwave absorption in two-dimensional heterostructures with broken translational symmetry qualitatively confirmed theoretical predictions made in the one-mode approximation [11, 12] for some fractional states from the Jain hierarchy of the fractional quantum Hall effect [13, 14]. However, any conclusions on the statistical properties of magnetorotons from these experiments cannot be made because such excitations have short lifetimes [9], which make impossible experimental manipulations with macroscopic ensembles of these excitations.

The possibility of the fabrication and study of a long-lived nonequilibrium ensemble of neutral excitations by optical methods was described for a 2DES in the regime of the integer quantum Hall insulator \(\nu = 2\) [15]. Despite a significant similarity with the equilibrium electron–hole state of the \(\frac{1}{2} + \frac{1}{2}\) quantum Hall effect, which was detected in bilayer electron systems [16, 17], nonequilibrium ensembles of neutral excitations observed at a filling factor of 2 have some features distinguishing them from other condensed states of electron matter [15, 18]. It appears that a necessary condition for the formation of a macroscopic ensemble of neutral excitations is that excitations with change in the total spin of the electron system that are inactive in the interaction with light (dark excitations with spin) are the lowest in energy. Such excitations are formed through the relaxation mechanisms to the lowest excited state after the energy deposition into the electron system through allowed high-energy optical transitions. In this case, macroscopic nonequilibrium ensembles of these excitations can be formed because the relaxation time of the lowest energy excitations is long since it is necessary to change the spin of the electron system and to simultaneously emit numerous phonons with certain energies. At first glance, this variant seems impossible in 2DESs at \(\nu = 1{\text{/}}3\) because in the one-mode approximation, which proves its efficiency in the description of neutral excitations with spin 0, it is predicted that the only excitation with spin 1 is a spin exciton active in the emission of an EPR photon whose dispersion is similar to the dispersion of a spin exciton in a Hall ferromagnet at \(\nu = 1\) [19]. At the same time, the exact solution of the Schrödinger equation for a multiparticle electron system indicates that excitations with spin 1 and the momentum about the inverse magnetic length, which can have the energy lower than the minimum energy of magnetorotons, appear in the \(\nu = 1{\text{/}}3\) fractional state [20]. This result ignored the contribution to the energy of these excitations from the single-particle Zeeman energy proportional to the magnetic field. Consequently, it is still unclear whether or not neutral excitations with spin 1 can have a lower energy than magnetorotons, at least, in high-mobility GaAs/AlGaAs quantum wells. In this work, we report the results of solving the Schrödinger equation for the two-dimensional electron system at \(\nu = 1{\text{/}}3\) with a finite number of particles. According to these results, excitations with change in the spin of the electron system by unity are the lowest in energy at certain parameters of the confining potential of the AlGaAs/GaAs quantum well.

We consider a 2DESs with the Coulomb interaction and periodic boundary conditions in a rectangular cell \(\Lambda \ni z = \alpha {{\tau }_{1}} + \beta {{\tau }_{2}}\), \(0 \leqslant \alpha ,\;\beta \leqslant 1\), where z is the complex coordinate and τ1 and τ2 are the vectors of the cell. Let the magnetic field B be perpendicular to the plane of the 2DES and \({{N}_{s}}\) magnetic flux quanta pass through the cell. The single-electron spectrum of this system consists of discrete Landau levels ℏωc(n + 1/2), where ωc = eB/m is the cyclotron frequency and n is an integer. The degree of degeneracy of a Landau level is \({{N}_{s}}\). The basis states for the system of \({{N}_{e}}\) electrons can be obtained by diagonalizing the kinetic part of the Hamiltonian \(\prod\nolimits_{j = 1}^{{{N}_{e}}} a_{{{{i}_{j}},{{n}_{j}}}}^{\dag }{\text{|}}0\rangle \). The pair interaction is specified by the expression

$${{\hat {H}}_{{\text{C}}}} = \sum\limits_{\alpha ,\beta } \sum\limits_{{{i}_{1}},{{i}_{2}},{{i}_{3}},{{i}_{4}}} \sum\limits_{{{n}_{1}},{{n}_{2}},{{n}_{3}},{{n}_{4}}} V_{{{{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}}}^{{{{n}_{1}}{{n}_{2}}{{n}_{3}}{{n}_{4}}}}a_{{\alpha ,{{i}_{1}},{{n}_{1}}}}^{\dag }a_{{\beta ,{{i}_{2}},{{n}_{2}}}}^{\dag }{{a}_{{\beta ,{{i}_{3}},{{n}_{3}}}}}{{a}_{{\alpha ,{{i}_{4}},{{n}_{4}}}}},$$
(1)

where \(a_{{\alpha ,{{i}_{k}},{{n}_{k}}}}^{\dag }\) and \({{a}_{{\alpha ,{{i}_{k}},{{n}_{k}}}}}\) are the creation and annihilation operators of the kth electron with the spin α in the \(\psi _{i}^{n}\) state, n is the number of the Landau level (\(0 \leqslant n < \infty \)), and i is the number of states in the Landau level (\(1 \leqslant i \leqslant {{N}_{s}}\)).

To determine the energy spectrum of this system, it is necessary to calculate the matrix elements of the Coulomb potential and to diagonalize the Hamiltonian (1). Let the cyclotron energy ℏωC and the Zeeman splitting energy be much higher than the Coulomb energy of electrons \(\frac{{{{e}^{2}}}}{{\epsilon {{l}_{B}}}}\). Then, the contribution from the upper Landau levels can be neglected and all electrons can be assumed spin polarized. In this case, it is sufficient to take into account a finite number of matrix elements for the exact diagonalization. The Fock basis for the electron system of \({{N}_{e}}\) electrons occupying \({{N}_{s}}\) possible states consists of \(C_{{{{N}_{s}}}}^{{{{N}_{e}}}}\) vectors; therefore, the exact diagonalization even for simple fractions is a very difficult problem. However, in view of the existence of an operator \(\gcd ({{N}_{e}},{{N}_{s}})\) [21] similar to the momentum operator, it is possible to develop a simpler scheme.

The Hamiltonian of the electron in a static magnetic field has the form \(\hat {H} = \frac{1}{{2m}}{{\left( {\hat {p} - \frac{e}{c}A} \right)}^{2}}\). A single-electron state in the lowest Landau level can be represented as [22]

$$\psi (x,y) = f(z)\exp \left( { - \frac{{{{y}^{2}}}}{{2l_{B}^{2}}}} \right),\quad z = x + iy.$$
(2)

The translation operator in the magnetic field \({{\hat {t}}_{m}}(\tau ) = \exp \left( {\frac{i}{\hbar }\left( {\hat {p} - \frac{e}{c}A} \right)\tau } \right)\) satisfies periodic boundary conditions \({{\hat {t}}_{m}}({{\tau }_{{1,2}}})\psi = \psi \). In the Landau calibration, \(\hat {A} = \left( {\begin{array}{*{20}{c}} 0 \\ {Bx} \end{array}} \right)\); consequently, in the Campbell–Hausdorff formula,

$${{\hat {t}}_{m}}(\tau ) = \exp \left( {\frac{{i{{\tau }_{x}}{{\tau }_{y}}}}{{2l_{B}^{2}}}} \right)\exp \left( {\frac{{i{{\tau }_{y}}x}}{{l_{B}^{2}}}} \right)\hat {t}(\tau ),$$
(3)
$${{\hat {t}}_{m}}({{\tau }_{1}}){{\hat {t}}_{m}}({{\tau }_{2}}) = \exp \left( {\frac{{i\left( {{{\tau }_{{1x}}}{{\tau }_{{2y}}} - {{\tau }_{{1y}}}{{\tau }_{{2x}}}} \right)}}{{l_{B}^{2}}}} \right){{\hat {t}}_{m}}({{\tau }_{2}}){{\hat {t}}_{m}}({{\tau }_{1}}),$$
(4)

where \(\hat {t}(\tau )\) corresponds to transfer by \(\tau = {{\tau }_{x}} + i{{\tau }_{y}}\). For a state to hold under translation, the \(\hat {t}({{\tau }_{1}})\) and \(\hat {t}({{\tau }_{2}})\) operators should commute:

$${{\tau }_{{1x}}}{{\tau }_{{2y}}} - {{\tau }_{{1y}}}{{\tau }_{{2x}}} = 2\pi {{N}_{s}}l_{B}^{2},\quad {{N}_{s}} \in \mathbb{Z}.$$
(5)

Applying Eq. (3) to Eq. (2) and taking into account that \({{\hat {t}}_{m}}({{\tau }_{{1,2}}})\psi = \psi \), we obtain the following condition on  f:

$$\frac{{f(z + {{\tau }_{i}})}}{{f(z)}} = \exp \left( { - \frac{{i({{\tau }_{i}} + 2z){{\tau }_{{iy}}}}}{{2l_{B}^{2}}}} \right).$$
(6)

Specifying \({{\tau }_{1}} \in \mathbb{R}\), \({{\tau }_{2}} = {\text{|}}{{\tau }_{2}}{\text{|}}{{e}^{{i\theta }}}\) (note that Eq. (5) gives \({{\tau }_{1}}{\text{|}}{{\tau }_{2}}{\text{|}}\sin \theta = 2\pi {{N}_{s}}l_{B}^{2}\)), we get \(\frac{{f(z + {{\tau }_{1}})}}{{f(z)}} = 1\) and, thereby, represent f in the form of a Fourier series: \(f(z) = \sum\nolimits_{k \in \mathbb{Z}} {{c}_{k}}\exp \left( {i\frac{{2\pi kz}}{{{{\tau }_{1}}}}} \right)\). Substituting it into Eq. (6), we obtain

$${{c}_{{k + {{N}_{s}}}}} = \exp \left( {\frac{{i{{\tau }_{2}}\pi {{N}_{s}}}}{{{{\tau }_{1}}}}} \right)\exp \left( {i\frac{{2\pi k{{\tau }_{2}}}}{{{{\tau }_{1}}}}} \right){{c}_{k}}.$$
(7)

The function \(f(z)\) corresponding to states of the lowest Landau level and the periodic boundary condition constitutes a linear space with the dimension \({{N}_{s}}\), so that

$$\begin{gathered} {{f}_{r}}(z) = \sum\limits_{m \in \mathbb{Z}} \exp \left( {i\frac{{m(m{\text{|}}{{\tau }_{2}}{\text{|}}\sin \theta + 2{{X}_{r}}){\text{|}}{{\tau }_{2}}{\text{|}}{{e}^{{i\theta }}}}}{{2l_{B}^{2}}}} \right) \\ \times \;\exp \left( {i\frac{{\left( {{{X}_{r}} + m{\text{|}}{{\tau }_{2}}{\text{|}}\sin \theta } \right)z}}{{l_{B}^{2}}}} \right),\quad {{X}_{r}} = \frac{{2\pi l_{B}^{2}r}}{{{{\tau }_{1}}}}. \\ \end{gathered} $$
(8)

The wavefunctions in the lowest Landau level have the form

$${{\psi }_{r}}(x,y) = {{\left( {\frac{1}{{{{\tau }_{1}}\sqrt \pi {{l}_{B}}}}} \right)}^{{\frac{1}{2}}}}$$
$$ \times \;\sum\limits_{m \in \mathbb{Z}} \exp \left( {i\frac{{({{m}^{2}}{\text{|}}{{\tau }_{2}}{{{\text{|}}}^{2}}\sin \theta + 2{{X}_{r}}m{\text{|}}{{\tau }_{2}}{\text{|}})\cos \theta }}{{2l_{B}^{2}}}} \right)$$
$$ \times \;\exp \left( {i\frac{{\left( {{{X}_{r}} + m{\text{|}}{{\tau }_{2}}{\text{|}}\sin \theta } \right)x}}{{l_{B}^{2}}}} \right)$$
$$ \times \;\exp \left( { - \frac{{{{{(y + {{X}_{r}} + m{\text{|}}{{\tau }_{2}}{\text{|}}\sin \theta )}}^{2}}}}{{2l_{B}^{2}}}} \right).$$

Similarly, in the nth Landau level,

$$\begin{gathered} \psi _{r}^{n} = {{\left( {\frac{1}{{{{L}_{1}}\sqrt \pi {{2}^{n}}n!{{l}_{B}}}}} \right)}^{{\frac{1}{2}}}}\sum\limits_{m \in \mathbb{Z}} {{e}^{{im\left( {2\pi j\frac{{{{L}_{2}}\cos \theta }}{{{{L}_{1}}}}} \right)}}}{{e}^{{i\frac{{{{m}^{2}}L_{2}^{2}\sin 2\theta }}{{4l_{B}^{2}}}}}}\exp \left( {i\frac{{\left( {{{X}_{r}} + m{{L}_{2}}\sin \theta } \right)x}}{{l_{B}^{2}}}} \right) \\ \times \;\exp \left( { - \frac{{{{{(y + {{X}_{r}} + m{{L}_{2}}\sin \theta )}}^{2}}}}{{2l_{B}^{2}}}} \right){{H}_{n}}\left( {\frac{{y + {{X}_{r}} + m{{L}_{2}}\sin \theta }}{{{{l}_{B}}}}} \right). \\ \end{gathered} $$
(9)

Finally, it is necessary to estimate the matrix elements of Eq. (1). In regard to the translation invariance of wavefunctions, they can be represented in the form

$$\begin{gathered} A_{{{{j}_{1}}{{j}_{2}}{{j}_{3}}{{j}_{4}}}}^{{{{n}_{1}}{{n}_{2}}{{n}_{3}}{{n}_{4}}}} \\ = \int\limits_\Lambda {d{{r}_{1}}} \int\limits_\Lambda {d{{r}_{2}}} \psi _{{{{j}_{1}}}}^{{{{n}_{1}} * }}({{r}_{1}})\psi _{{{{j}_{2}}}}^{{{{n}_{2}} * }}({{r}_{2}})\tilde {V}({{r}_{1}} - {{r}_{2}})\psi _{{{{j}_{3}}}}^{{{{n}_{3}}}}({{r}_{2}})\psi _{{{{j}_{4}}}}^{{{{n}_{4}}}}({{r}_{1}}), \\ \end{gathered} $$
(9a)

where \(\tilde {V}(r) = \sum\nolimits_{{{k}_{1}},{{k}_{2}}} \frac{{{{e}^{2}}}}{{{\text{|}}r + {{k}_{1}}{{\tau }_{1}} + {{k}_{2}}{{\tau }_{2}}{\text{|}}}}\). This doubly periodic function can be expanded in the Fourier series \(\tilde {V}(z) = \frac{{2\pi l_{B}^{2}}}{\sigma }\sum\nolimits_{q \in {{L}^{{ - 1}}}} \frac{{{{e}^{2}}}}{q}\exp (i(q,r))\), where σ is the area of the unit cell, \(L = \{ {{k}_{1}}{{\tau }_{1}} + {{k}_{2}}{{\tau }_{2}}, {{k}_{1}},{{k}_{2}} \in \mathbb{Z}\} \), and summation is performed over the reciprocal lattice \({{L}^{{ - 1}}}\), \(\forall q \in {{L}^{{ - 1}}}\), \(r \in L\) \((q,r) = 2\pi N\), \(N \in \mathbb{Z}\).

To take into account the geometric damping of the Coulomb interaction, the Fourier component of the Coulomb potential was supplemented with the geometric form factor \(F(q)\) calculated in terms of the envelope profile of the wavefunction of electrons in the lowest subband of the conduction band in the GaAs/AlGaAs quantum well:

$$\tilde {V}(z) = \frac{{2\pi l_{B}^{2}}}{\sigma }\sum\limits_{q \in {{L}^{{ - 1}}}} \frac{{{{e}^{2}}F(q)}}{q}\exp (i(q,r)).$$
(10)

The substitution of Eqs. (9) and (10) into Eq. (9a) gives

$$A_{{{{j}_{1}}{{j}_{2}}{{j}_{3}}{{j}_{4}}}}^{{{{n}_{1}}{{n}_{2}}{{n}_{3}}{{n}_{4}}}} = \frac{{2{{e}^{2}}}}{\sigma }\sum\limits_{q \in {{L}^{{ - 1}}}} \frac{{F(q)}}{q}{{\mathcal{G}}^{{{{n}_{1}},{{n}_{4}}}}}(q){{\mathcal{G}}^{{{{n}_{2}}{{n}_{3}}}}}( - q),$$
(11)

where

$$\begin{gathered} {{\mathcal{G}}^{{{{n}_{s}}{{n}_{t}}}}}(q) = \sqrt \pi \exp \left( {i\frac{{2{{\pi }^{2}}\cot \theta l_{B}^{2}}}{{\tau _{1}^{2}}}\left( {{{j}_{s}} - {{j}_{t}} - \frac{{{{q}_{x}}{{\tau }_{1}}}}{{2\pi }}} \right)\left( {{{j}_{s}} + {{j}_{t}} - \frac{{{{q}_{x}}{{\tau }_{1}}}}{{2\pi }}} \right)} \right)\exp \left( {i{{q}_{y}}\left( {{{X}_{{{{j}_{s}}}}} + \frac{{{{q}_{x}}l_{B}^{2}}}{2}} \right)} \right){{e}^{{ - {{{\left( {\frac{1}{2}lq} \right)}}^{2}}}}} \\ \times \;\sqrt {\frac{{\min ({{n}_{s}},{{n}_{t}})!}}{{\max ({{n}_{s}},{{n}_{t}})!}}} {{\left( {\frac{{l({\text{sgn}}({{n}_{t}} - {{n}_{s}}){{q}_{x}} + i{{q}_{y}})}}{{\sqrt 2 }}} \right)}^{{|{{n}_{s}} - {{n}_{t}}|}}}L_{{\min ({{n}_{s}},{{n}_{t}})}}^{{|{{n}_{s}} - {{n}_{t}}|}}\left( {\frac{{{{q}^{2}}{{l}^{2}}}}{2}} \right)\delta {\kern 1pt} {{'}_{{\frac{{{{q}_{x}}{{\tau }_{1}}}}{{2\pi }} + {{j}_{t}} - {{j}_{s}}}}}. \\ \end{gathered} $$
(12)

Here, \(L_{n}^{k}\) is the generalized Laguerre polynomial.

The function \(F(q)\) was calculated with the real parameters of the experimental sample and was then approximated by the expression \(F(q) = \frac{{1.5060801}}{{q + 1}} - \) \(\frac{{0.48825941}}{{{{{(q + 1)}}^{2}}}}\) – 0.02609079. The simulation was performed for the 2DES in GaAs with the parameters \(\varepsilon = 12.5\), \(m\text{*} = 0.067{{m}_{0}}\), and \({{n}_{e}} = 8 \times {{10}^{{10}}}\) cm–2.

To verify the accuracy of our calculation scheme, we first compared the dispersion relation of spin excitons analytically calculated for the \(\nu = 1\) Hall ferromagnetic [19] with the numerical solution of the Schrödinger equation for the system of 28, 29, and 30 electrons. Figure 1 demonstrates that the two results are in good agreement with each other. Second, we compared the solutions of the Schrödinger equation for the system of seven, eight, and nine particles in the \(\nu = 1{\text{/}}3\) state with the dispersion relation of magnetorotons obtained in the one-mode approximation [11, 12]. It is seen that the numerical results for the magnetoroton branch coincide with the results in the one-mode approximation at momenta below the inverse magnetic length (Fig. 2).

Fig. 1.
figure 1

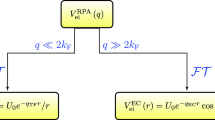
(Color online) (Circles) Data obtained by solving the Schrödinger equation for the ideal 2DES of 28, 29, and 30 electrons in an external magnetic field of 10 T (the s-ingle-particle Zeeman energy is assumed zero and the geometric form factor is unity). The solid line is the energy calculated by the formula \({{E}_{0}}(q) = \frac{{{{e}^{2}}}}{{\epsilon {{l}_{B}}}}{{\left[ {\frac{\pi }{2}} \right]}^{{1/2}}} \times \) \(\left[ {1 - {{e}^{{ - {{q}^{2}}l_{0}^{2}/4}}}{{I}_{0}}\left( {\frac{{{{q}^{2}}l_{0}^{2}}}{4}} \right)} \right]\) from [19], where \({{I}_{0}}\) is the modified Bessel function and lB is the magnetic length. The inset shows the layout of the spin exciton.

Full size image
Fig. 2.
figure 2

(Color online) Energies of neutral excitations in the \(\nu = 1{\text{/}}3\) fractional state calculated by solving the Schrödinger equation for the 2DES of seven, eight, and nine electrons with the GaAs/AlGaAs δ quantum well in an external magnetic field of 10 T. Green circles correspond to the branch of magnetorotons and violet circles are the two lowest branches of the continuum of birotons. The green dashed and violet solid lines are plotted for convenience. The red solid line is the magnetoroton dispersion analytically calculated in the one-mode approximation. The insets show the layouts of the magnetoroton (MR) and biroton (MG) with zero spin.

Full size image

A minimum in the dispersion relation of magnetorotons at momenta near one and a half magnetic lengths is also reproduced, although it is deeper than the prediction of the one-mode approximation. In addition to the magnetoroton branch, the dispersion relation includes the continuum of oscillations of the electron density with a total angular momentum of 2, which agrees with assumptions made in [23]. Below, these neutral excitations are called magnetorotons according to the terminology accepted for such excitations [23–25] or birotons, which are closer to the intuitive representation on the nature of these excitations. Birotons with zero spin near \(q = 0\) are systems of two magnetorotons with opposite momenta of the same magnitude [26]. The energy of the biroton with zero momentum is minimal and is equal to the double energy of the roton minimum (disregarding the interaction between the magnetorotons). The other double combinations of magnetorotons have higher energies and, correspondingly, the dispersion of birotons is positive.

The main result of our calculations is the revealed excitation branch with the energy lower than that of magnetorotons. To understand the nature of this branch, we consider the dispersion relation for the three lowest excitations with spin 1 (Fig. 3). The existence of the spin exciton (excitation in the lowest Landau level with spin flip) is in agreement with the prediction in the one-mode approximation [20]. However, in addition to this excitation, the spectrum contains combined branches of spin–charge excitations with simultaneous oscillations of the charge density in the lower spin sublevel of the lowest Landau level and spin flip. We refer to these excitations as birotons with spin 1 because they can be represented as combinations of magnetorotons with spins 0 and 1. The energies of spin biroton and spin exciton branches become equal to each other at a certain momentum, which results in the repulsion between these branches and in the formation of local energy minima. Correspondingly, the spin branch with the lowest energy at nearly zero momenta behaves as the spin exciton branch, whereas this branch at momenta about the inverse magnetic length becomes the spin magnetoroton branch. In this case, this branch in the GaAs/AlGaAs δ quantum well has the lowest energy among all neutral excitations in the electron system.

Fig. 3.
figure 3

(Color online) Energies of excitations with spin 1 in the \(\nu = 1{\text{/}}3\) fractional state calculated by solving the Schrödinger equation for the 2DES of seven, eight, and nine electrons with the GaAs/AlGaAs δ quantum well in an external magnetic field of 10 T. Blue circles correspond to spin excitons and violet circles are the two lowest branches of the continuum of birotons with spin 1. The red solid line is the dispersion spin rotons analytically calculated in the one-mode approximation. The insets show the layouts of the spin exciton (SE) and spin biroton (SMG).

Full size image

To use the above results in experiments, it is necessary to determine whether the geometric form factor, which is due to the nonlocality of the electron wavefunctions in the growth direction of semiconductor heterostructures with GaAs/AlGaAs quantum well and reduces the Coulomb interaction [27], and the single-particle Zeeman energy [28] can affect the calculated energies of excitations and whether the branches of spin excitations will still have the lowest energy. Figure 4 presents the dependences of the energies of roton minima on the magnetic field and width of the quantum well. Below a certain critical magnetic field, the branch of excitations with spin 1 has the lowest energy. In this case, the combination of magnetorotons with spins 0 and 1, i.e., the biroton with spin 1, will have the energy below the energy of the biroton with spin 0. Thus, the spin exciton with the single-particle Zeeman energy and the spin biroton will have the lowest energies among neutral excitations in the electron system.

Fig. 4.
figure 4

(Color online) Magnetic field dependences of the energies of roton minima for birotons with spin (green circles) 0 and (blue circles) 1 for the 20-nm-wide GaAs/AlGaAs quantum well calculated by solving the Schrödinger equation for the 2DES of seven, eight, and nine electrons. The upper inset shows the energies of roton minima at 10 T versus the width of the quantum well. The single-particle Zeeman energies for different widths of the well are taken from [27]. The lower inset shows the critical magnetic field at which the energies of roton minima for excitations with spins 0 and 1 become equal to each other versus the width of the quantum well.

Full size image

To summarize, a calculation scheme has been developed to determine the dispersion relations of neutral excitations in the 1/3 quantum Hall effect state. It has been shown that experimental conditions for the formation of a macroscopic ensemble of neutral excitations with spin 1 can be ensured under certain constraints on the magnetic field (electron density) and the width of the GaAs/AlGaAs quantum well. There are two low-energy branches of spin excitations at zero pulse (most simply implementable experimental situation): spin exciton and spin biroton (magnetic graviton). A macroscopic ensemble of spin excitons under the steady-state optical excitation of the electron system cannot be formed because the lifetime of these excitations is too short [28], whereas the formation of a macroscopic ensemble of spin birotons (magnetic gravitons) is quite realistic [29].