Method of Angular Invariants: Experiment

A method for the precise measurement and an algorithm for the calculation of the refractive index of transparent optical materials have been proposed excluding the interaction length of probe radiation with a sample from observables. The angular invariants of the reflection/transmission coefficient have been experimentally determined for the first time. The method has been implemented in practice with plane parallel sapphire plates.

INTRODUCTION

“Although various well-developed methods for the determination of the optical parameters of crystals exist, the development of new methods that supplement the existing methods and are free of some their disadvantage is still relevant” (F.I. Fedorov, 1958 [1]).

Methods for the measurement of refractive indices of optical materials are very diverse [2–4]. The choice of a certain method is determined by a certain object under study and the aim of measurement with certain instruments and required accuracy. The precise measurement of refractive indices has been recently become of great interest [5–7] because of increasing productivity, as well as complex simulation and fabrication, currently required for waveguide-based devices [8, 9]. The refractive indices of the materials used in these devices should be known with an accuracy of 10⁻⁴. The precise measurement of refractive indices is an important element of the technology of design of optical devices with a high resolution, a large numerical aperture, and minimum spherical and chromatic aberrations [3]. Existing methods ensuring a high accuracy require the preparation of samples in the form of sufficiently large prisms with well-processed faces, as well as prespecified angles and sizes of the faces. Such a preparation is very expensive, and measurements can hardly be automated and can take several hours. The main disadvantage is that the calculation of refractive indices using these methods involves the perfect interface model, which is incompatible with the requirement of the necessarily high accuracy.

In most cases, an obligatory condition for the calculation of refractive indices from measured observables is the direct measurement of the interaction length of probe radiation with a material. This requirement does not concern the calculation of refractive indices from the measured Brewster angle, i.e., the angle of incidence of probe radiation polarized in the plane of incidence at which the energy reflection coefficient (R coefficient) is minimal. Despite obvious simplicity, this method is hardly used because it imposes stringent requirements on the formation of the interface between the sample and environment. The correct application of the method was described in [10]. In [11], we proposed to use the angular positions of three successive interference minima formed upon the reflection of a monochromatic electromagnetic plane wave polarized in the plane of incidence (p wave) from the interface as observables. Invariant relations existing between these angles allow one to exclude the length of interaction of probe radiation with the sample from observables used to calculate refractive indices. In this work, we propose an experimental method to determine invariants of reflection/transmission coefficients ($R{\text{/}}T$ coefficients) based on the described foundation and an algorithm to calculate the refractive indices of a transparent optical material.

MODEL OF INVARIANTS

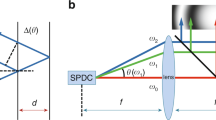
For a plane–parallel plate with ideal interfaces (buffer-layer thicknesses ${{d}_{2}} = 0$ in Fig. 1), the angular positions of the minima of the R coefficient in the transparency region coincide with the angular positions of the maxima of the T coefficient of the p wave. The angles of incidence θ_m at which the R coefficient has minima or the T coefficient has maxima are determined by the following interference condition on the phase thickness of the plate ψ:

$$\psi = 2\pi \frac{{{{d}_{3}}}}{\lambda }\sqrt {n_{3}^{2} - n_{1}^{2}{{{\sin }}^{2}}{{\theta }_{m}}} = \pi m.$$

Fig. 1.

(Color online) Layout of the symmetric five-layer structure.

Here, n₁ and n₃ are the refractive indices of the media, d₃ is the thickness of the plate, λ is the wavelength of probe radiation, and m is the absolute number identifying extrema, which is maximal for the extremum closest to the normal and decreases with an increase in the angle of incidence. According to this condition,

$${{\sin }^{2}}{{\theta }_{m}} = \frac{{n_{3}^{2}}}{{n_{1}^{2}}} - \frac{1}{{n_{1}^{2}}}{{\left( {\frac{\lambda }{{{{d}_{3}}}}\frac{m}{2}} \right)}^{2}}.$$

(1)

The following invariant relations exist between the angles of interference extrema θ_m [10]:

$${\text{In}}{\kern 1pt} {{v}_{\varepsilon }} = {{\sin }^{2}}{{\theta }_{m}} - \frac{{4{{{\sin }}^{2}}{{\theta }_{{m + 1}}} - 3{{{\sin }}^{2}}{{\theta }_{m}} - {{{\sin }}^{2}}{{\theta }_{{m + 2}}}{{)}^{2}}}}{{8({{{\sin }}^{2}}{{\theta }_{{m + 2}}} - 2{{{\sin }}^{2}}{{\theta }_{{m + 1}}} + {{{\sin }}^{2}}{{\theta }_{m}})}};$$

$${\text{In}}{\kern 1pt} {{v}_{d}} = {{\sin }^{2}}{{\theta }_{{m + 2}}} - 2{{\sin }^{2}}{{\theta }_{m}} + {{\sin }^{2}}{{\theta }_{m}}.$$

The parameters In ${{v}_{\varepsilon }}$ and In ${{v}_{d}}$ include only angular coordinates and are constant for the chosen material of the plate. The refractive index ${{n}_{3}}$ and thickness of the plate ${{d}_{3}}$ are expressed by the simple formulas

$${{n}_{3}} = {{n}_{1}}\sqrt {{\text{In}}{\kern 1pt} {{v}_{\varepsilon }}} ;\quad {{d}_{3}} = \frac{\lambda }{{\sqrt { - 2{\text{In}}{{v}_{d}}} }}.$$

(2)

The absolute number of an extremum is also determined only by angular coordinates as

$$m = \frac{{4{{{\sin }}^{2}}{{\theta }_{{m + 1}}} - 3{{{\sin }}^{2}}{{\theta }_{m}} - {{{\sin }}^{2}}{{\theta }_{{m + 2}}}}}{{2({{{\sin }}^{2}}{{\theta }_{{m + 2}}} - 2{{{\sin }}^{2}}{{\theta }_{{m + 1}}} + {{{\sin }}^{2}}{{\theta }_{m}})}}.$$

We include it in the set of experimental observables. At the points of extrema of the R and T coefficients, the internal parameters of the structure (${{n}_{3}}$ and ${{d}_{3}}$) are separated and can be determined independently. It is convenient to represent the set of angular positions of extrema ${{\theta }_{m}}$ in the form of a column vector θ. The length M of θ is equal to the number of minima in the entire range of angles of incidence and is unam-biguously determined by the parameters of the structure [11]:

$$M = {{m}_{{\max }}} - {{m}_{{\min }}},$$

$${{m}_{{\max }}} = 2\left[ {\frac{{{{d}_{3}}}}{\lambda }{{n}_{3}}} \right];\quad {{m}_{{\min }}} = 2\left[ {\frac{{{{d}_{3}}}}{\lambda }\sqrt {n_{3}^{2} - n_{1}^{2}} } \right].$$

(3)

We also include M in the set of experimental observables.

In the experimental implementation of the method of invariants, it is necessary to take into account that almost any method of processing of the surface of the sample inevitably leads to the deviation of the composition/structure of the subsurface layer of the sample and the buffer layer from the composition/structure of its bulk [12]. For this reason, the refractive index and thickness calculated by Eqs. (2) are considered as the zeroth-approximation values for a more complex mathematical model taking into account the presence of buffer layers. Such a model can be a symmetric five-layer structure (Fig. 1). We assume that the refractive indices and thicknesses are the same for all buffer layers. This is valid for the identical method and quality of processing of surfaces. The thicknesses of buffer layers are assumed much smaller than the thickness of the plate. However, they are mainly responsible for the absorption of probe radiation. For this reason, the imaginary addition to the refractive index of the buffer layer should be included in the model:

$${{\tilde {n}}_{2}} = {{n}_{2}} + i{{k}_{2}}.$$

The algorithm for the calculation of the parameters of the symmetric five-layer structure using the known angular positions of extrema of θ is illustrated by a numerical experiment with the test parameters {n₁ = 1.0, n₂ = 1.73, n₃ = 1.77, n₂ = 1.73, n₁ = 1.0} and {d₂ = 20.0 nm, d₃ = 447 000.0 nm, d₂ = 20.0 nm} close to the experimental situation. The algorithm can be described as follows.

—The positions of the extrema of θ^t of the test structure are calculated from the angular dependence of the T coefficient of the five-layer structure [4, 13].

—The refractive index ${{n}_{3}}$ and thickness of the plate ${{d}_{3}}$ are calculated by Eqs. (2) using the dependence of the extrema of the transmission coefficient on the number of an extremum enumerated from the normal.

—The column vector Δ = θ^t – θ^p of differences between the test, θ^t, and probe, θ^p, structures is constructed.

—The minimum of the goal function

$$F({{d}_{i}},{{n}_{i}}) = {{\left| \Delta \right|}^{2}}$$

(4)

is calculated by varying the parameters of the structure ${{d}_{2}}$, ${{d}_{3}}$, ${{\tilde {n}}_{2}}$, and ${{n}_{3}}$ with the constant total thickness of the plate $d = {{d}_{3}} + 2{{d}_{2}}$.

The goal function (4) has the following important features.

(i) Only the angular positions of extrema are taken into account to calculate $F({{d}_{i}},{{n}_{i}})$. The amplitudes of the T coefficient, which provide significant errors, are not involved in the calculation. This is an advantage of the goal function given by Eq. (4) compared to goal functions which usually require two parameters (e.g., the angle of incidence ${{\varphi }_{1}}$ and the R coefficient), both determined with a certain error in the calculation of deviations.

(ii) The displacement of extrema at the divergence of the light beam less than 2 × 10^–3 rad is less than 2 × 10^–5 rad and weakly affects the minimization result.

The result of minimization of the goal function of the test problem in the coordinates $\{ {{n}_{3}},{{d}_{3}}\}$ is presented in Fig. 2. The dynamics in other coordinates {n₂, n₃}, {n₂, d₃}, etc., of the goal function $F({{d}_{i}},{{n}_{i}})$ is similar. The analysis shows that the minimum of the goal function $F({{d}_{i}},{{n}_{i}})$ unambiguously determines all four input parameters of the structure and, thus, the method is promising for an experimental implementation.

Fig. 2.

(Color online) (a) Dynamics of minimization of the goal function $F({{d}_{3}},{{n}_{3}})$ in approximation of the probe parameters of the structure to the test parameters. (b) Dynamics of minimization of the goal function $F({{d}_{3}},{{n}_{3}})$ with respect to experimental values of the angular positions of extrema of the T coefficient.

EXPERIMENT

The angular dependences of the T coefficient were measured on a bench whose main elements are presented in Fig. 3. A beam from an infrared radiation source (BLD-1550-BF-20 single-frequency solid-state laser, the wavelength at T = 25°C is λ = 1549.66 nm, and the radiation bandwidth is Δf = 100 kHz) passes through a Glan prism and sample placed on the adjusting unit and detected by a photodetector. The adjusting unit with the sample placed on it ensures the following:

Fig. 3.

(Color online) Layout of the experimental bench: (1) single-frequency solid-state laser BLD-1550-BF-20, (2, 7) infrared photodetectors PM-100, (3) wedge-shaped beam splitter, (4) Glan prism, (5) adjusting unit based on a PC-controlled Thorlab HDR50 rotation stage, (6) sample, (8) automated control unit of the adjusting unit and recording the measured parameters.

—the adjustment of the sample in three coordinate axes and three rotation axes,

—the variation of angles of incidence of probe radiation on the sample in the range of ~180°,

—the angular positioning of the working surface of the sample along the vertical rotation axis with an accuracy of ~6″,

—the positioning of the probe radiation in the plane of the sample with an accuracy of ~1 μm,

—the alignment of the working surface of the sample with the vertical rotation axis,

—the positioning of the point of incidence of the probe radiation on the vertical rotation axis,

—the replacement of the sample and its adjustment in ~10 min,

—the automated data collection in the range of 180° in ~12 min.

The test of the bench showed that the 1/e aperture of probe radiation on the working surface of the sample is ~2 mm. The divergence of the beam is ~2.0 × 10^–3 rad. The standard deviation of the radiation intensity from the time-average value is no more than ~0.5%. The ellipticity of radiation passed through the Glan prism is ~2.0 × 10^–4. The alignment of the plane of incidence with the direction of polarization of incident radiation was ensured by rotating the Glan prism to establish the minimum of reflected signal at the angle of incidence close to the angle of the total polarization to the working surface of the sample. The intensities of radiation intensities incident on the sample and passed through it were measured simultaneously by two PM-100 infrared photodetectors. The standard deviation of the ratio of these signals from the time average was no more than ~0.01%. The dynamic measurement range of the reflection coefficient to test the bench was ~80 dB. The temperature of the room with the measuring bench was measured by a gauge located near the sample. The temperature during the experiment was (23.8 ± 0.25)°C.

The proposed algorithm for the determination of the parameters of the optical material was experimentally implemented on a sapphire plate (〈0001〉 orientation of the C plane) with a thickness of d = (444 ± 0.5) μm. In the preliminary experiments, the spatial distributions of the R-coefficient were measured at angles of incident ~10° and the position of the axis (edge) of the wedge plate was determined. The deviation of the reflection coefficient in the region of incidence of the beam from the average value did not exceed 0.2%. To exclude the effect of the slightly wedge shape of the plate on the positions of extrema, the sample was placed so that the axis (edge) of the wedge was parallel to the plane of incidence.

The working length of the emitter measured by the MDR-204 monochromator at T = 23.8°C was 1549.564 nm.

Figure 4 shows the experimental angular dependence of the T coefficient in the range of angles of incidence of 100°. The right part of the dependence (0°–90°) includes $N = 181$ extrema of the T coefficient. The first 130 extrema were used in further calculations. Using these experimental data, we calculated sin²θ, where θ is the angular position of extrema (red asterisks in Fig. 5), and, according to Eq. (1), the trend sin²θ quadratic in the number of the maximum (blue asterisks in Fig. 5). The coefficient of approximation of the trend is $R = 0.999999$, which indicates a high quality of processing of working surfaces of the experimental sample and confirms that the symmetric five-layer model with thin buffer layers can be used to treat experimental data.

Fig. 4.

(Color online) Angular dependence of the T-coefficient according to (red lines) experimental data and (blue lines) calculation with the minimization parameters.

Fig. 5.

(Color online) (Red asterisks) Angles of incidence at which the T-coefficient has extrema. The trend is indicated by blue asterisks. The first number from the normal corresponds to the maximum absolute number m = 998.

Further, the thickness and refractive index of the plate were calculated within the three-layer model with perfect interfaces. The resulting values d₃₀ = 444.151 μm and n₃₀ = 1.7365 are used as the input parameters for the five-layer model. The thickness of the plate d₃₀ is in agreement with a value of (444 ± 0.5) μm obtained in the direct measurement, and the refractive index n₃₀ is close to an expected value of 1.74. At the same time, the goal function $F({{d}_{3}},{{n}_{3}})$ is rather large (1.13 × 10^–3); i.e., the accuracy of the determination of the refractive index of the structure is worse than 10^–4.

The minimization of the goal function of the structure with buffer layers implies the search for a minimum in the fourth order phase space. To optimize the calculations, it is necessary to contract the range of variation of the maximum possible number of parameters. The range of minimization in the thickness d₃ is Δd₃ = 1 μm according to the data for the thickness of the used sapphire plate. The range of minimization in the refractive index of the plate n₃ is determined by the number of observed absolute maxima M. In our case, M = 181. Substituting the bound values of the thickness into Eqs. (3), we determine the range of minimization in the refractive index of the plate n₃ = n₃₀ ± 0.013. The range of minimization in the thickness of the buffer layer was 0–50 nm according to experimental values obtained for a number of glasses [10]. The refractive index of the buffer layer was varied from 1 to 3.

The dynamics of minimization of the goal function using experimental data obtained for sapphire is presented in Fig. 2b. The detailed analysis shows that $F({{d}_{i}},{{n}_{i}})$ reliably determines the parameters of the structure; they are summarized in Table 1. Although the fitting of functions with numerous extrema is a complex problem, it is successively solved with the proposed algorithm, as seen in Fig. 4.

Table 1. Optical parameters of the structures that are obtained with the minimization algorithm

Figure 4 shows the fragments of the angular dependences of the T coefficient in three ranges of angles of incidence: near the normal, near the Brewster angle (marked by the dashed vertical straight line), and behind the Brewster angle. The red lines present the experimental data. The blue lines are the dependences of the T coefficient directly calculated [4, 14] for the symmetric five-layer structure with the minimization parameters. The positions of extrema of both dependences visually coincide in the entire range of angles of incidence. At the same time, the amplitudes of the T coefficients are noticeably different. We note that each point of the angular dependence results from the interference of light waves in a Fabry–Perot interferometer formed by the working surfaces of the plane-parallel plate. The maximum $(T_{m}^{{\max }}$) and minimum $(T_{m}^{{\min }})$ T coefficients with the number m determine the contrast of the interference pattern $T_{m}^{{\max }}{\text{/}}T_{m}^{{\min }}$. It is seen that the calculated contrast is deeper than the experimental one. The contrast can be increased by more accurately processing the surfaces of the sample, by reducing the wedge angle of the structure, by reducing the diffraction divergence of the beam, and by other measures used to design classical Fabry–Perot interferometers. Our analysis shows that the proposed method is weakly sensitive to the small wedge angle of the structure and to the diffraction divergence of the light beam; such a weak sensitivity is an advantage of the method. The main result of the experiment is the demonstration that the parameters of the structure can be unambiguously determined from extrema of the T coefficient. The standard deviation of the angular positions of extrema θ^exp from their calculated values θ^min is ~17″. The distribution function of the standard deviations is presented in Fig. 6. As seen, it is an unbiased normal distribution.

Fig. 6.

(Color online) Distribution function of deviations of measured positions of extrema θ^exp from their calculated values θ^min.

The confidence interval at a C.L. of 0.99 for the parameters $\{ {{n}_{i}},{{d}_{i}}\}$ was obtained by the numerical calculation of the differential of the T coefficient at the minimization parameters for the extremum with the absolute value m = 948, at which the following parameters are maximal: Δd₂ = 5 nm, Δd₃ = 1.0 nm, Δn₂ = 0.03, Δn₃ = 4 × 10⁻⁶, and Δk₃ = 0.003.

As seen, the confidence interval of the refractive index plate n₃ corresponds to the best methods for the measurement of refractive indices of optical materials. The performed measurements and calculations indicate that the proposed interference method for the measurement of refractive indices together with the previously established [11] angular invariants of the R/T coefficients is precise. Furthermore, the application of the invariants allows the separate measurements of the refractive index and the thickness of the plate, which makes it possible to measure the absolute value of the refractive index.

CONCLUSIONS

A method for the precise measurement and an algorithm for the calculation of the optical parameters of solids have been proposed. The method is based on the model of the angular invariants of the reflection/transmission coefficients and does not require the measurement of the geometrical sizes of the sample. The independent measurement of the refractive index and thickness of the plate allows one to determine the absolute values of refractive indices. The method is a variant of the interference method for the measurement of refractive indices. The plane-parallel plate itself serves as a resonator. This is a significant advantage of the method compared to the classical Fabry–Perot optical interference scheme, where the resonator is formed by external mirrors. To ensure a high sensitivity of the classical scheme of the method in this case, “an experiment should be prepared very carefully and accurately” [14].

An advantage of the method is the inclusion of buffer layers in the model of the symmetric five-layer structure, which has been done for the first time. The proposed algorithm for minimization makes it possible to unambiguously reconstruct the parameters $\{ {{\tilde {n}}_{2}},{{n}_{3}},{{d}_{2}},{{d}_{3}}\}$ of the plane-parallel plate in the transparent range. The possibility of the measurement of refractive indices in an unlimited range is also an advantage of the method.

The measurement in transmission geometry simplifies the optical scheme of the method because it does not require the tuning of the position of the photodetector under the variation of the angle of incidence of radiation on the structure. This allows measurements in the range of angles of incidence from ‒90° to +90°, which is important for the proposed method. The transmission geometry is also favorable for the automation of the process of measurements.

The knowledge of the parameters of buffer layers is certainly important to design high-resolution optical devices, as well as nonlinear and integrated optical devices. The method can be efficient to determine the surface properties of optical materials at the finish processing stage. The method can be easily automated, which is important for serial control. We believe that this method is promising for applications in metrology, in particular, to create a refractive index standard.

The scheme of the experimental bench presented in Fig. 3 is a scheme of a new-type refractometer. The measurement of refractive indices requires a plane-parallel plate with well-processed working surfaces. Refractive indices have been calculated within the model of the symmetric five-layer structure including buffer layers of the structure. The measurement has been automated and takes no more than one hour.