BACKGROUND

A number of exciting and relatively recent publications (about ten years ago, compared to more than 100 years of the discovery of the classical liquid crystals) report on a discovery of a new type of equilibrium liquid crystals, termed twist–bend nematics, NTB (see [1–6]). The discovery of NTB nematics opened “Pandora box” with new kinds of modulated liquid crystals (see very influential pioneering works and reviews [7–19]). Naturally (as was the case in great geographical discoveries of XV–XVII centuries) after the first step devoted mainly to observations and structural identifications of new liquid crystals, the interest moves to investigations and exploring of physical properties of these new phases. Since then the NTB and other modulated nematics are becoming one of the hottest topics in physics of liquid crystals.

To start a few words about structural features of NTB nematics is in order here. Especially surprising is the fact that the twist–bend nematics, NTB, exhibit helical (chiral) orientational ordering despite being formed from achiral molecules. For comparison, there exist also chiral cholesteric phases locally equivalent to nematics but possessing simple (orthogonal) helical structures with pitches in a few micron range. The cholesteric structure appears as a result of relatively weak molecular chirality (that is why it has a relatively large pitch), and the swirl direction of the spiral (left or right) is determined by the sign of the molecular chirality. Unlike this situation, the NTB nematics are formed as a result of spontaneous chirality breaking, they have nanoscale (a few nanometers) pitch. This fact suggests that description of the twist–bend nematics in terms of an orientational elastic energy needs a modification related to relatively short pitch of the helicoidal structure. In the case the Frank moduli for the short-scale component of the director field are different from those for the long-scale component of the director. Therefore, the components should be treated in terms of different elastic energies. We keep the notation n for the long-scale component of the director (nematic director in what follows) and introduce its short-scale component φ. The components have to be orthogonal, \({\mathbf{n}} \cdot \boldsymbol{\varphi} = 0\). Thus, the vector φ has two independent components. The quantity \({\mathbf{n}} + \boldsymbol{\varphi} \) can be naturally termed as the NTB phase director. It has the helical conic structure in space. By other words, the short-scale component φ rotates around n at moving along the n-direction. Therefore, the absolute value of the vector φ gives the tilt angle θ for the conical spiral. Because the conical helical structure has a certain short pitch periodicity, it is characterized by the wave vector \({{q}_{0}}\), experimentally on the order of a few inverse molecular length.

This work is motivated by two very recent works [20, 21] on rheological studies of the NTB liquid crystals. The authors of these works found nontrivial non-Newtonian behavior of sheared NTB nematics. At relatively low shear rate (\(\dot {\gamma } \leqslant {{\dot {\gamma }}_{{c1}}}\)) the stress tensor σ created by this shear strain, scales as \(\sigma \propto {{\dot {\gamma }}^{{1/2}}}\). Thus, the effective viscosity decreases with the shear rate (\(\eta \propto {{\dot {\gamma }}^{{ - 1/2}}}\)) manifesting so-called shear-thinning phenomenon. At intermediate shear rate \({{\dot {\gamma }}_{{c1}}} \leqslant \dot {\gamma } \leqslant {{\dot {\gamma }}_{{c2}}}\), σ is almost independent of \(\dot {\gamma }\) (a sort of plateau), and at large shear rate (\(\dot {\gamma } \geqslant {{\dot {\gamma }}_{{c2}}}\), \(\sigma \propto \dot {\gamma }\)), and it looks like Newtonian rheology. The critical values of the shear rate (\({{\dot {\gamma }}_{{c1}}}{\kern 1pt} ,{\kern 1pt} {{\dot {\gamma }}_{{c2}}}\)) indicating transitions between dynamical regimes depend on the temperature. Above a certain temperature T* (below N–NTB phase transition point Tc, where N stands for conventional nematic state) the behavior becomes pure Newtonian. The aim of this work is to present theoretical rationalization for the results observed in [20, 21]. In what follows we integrate the input from recent works and discussions, however my own contribution to this field will be also presented.

Although the origin of the observed experimentally rheological behavior of the NTB nematics still remains to be clarified, the main message of this work is robust. Namely we claim that coarse grained dynamic description of the NTB phase allows one to rationalize qualitatively the observed in the phase different rheological regimes. Such coarse grained description supplemented by arguments based on the maximum rate of entropy production principle, can be used to estimate the critical values of the shear rate separating these rheological regimes. The estimations made in the work are applicable to the shearing of well-ordered samples of the NTB phase. If it is not the case, defects (disclinations or domain walls) affect the rheology. However, relying on the maximum entropy production rate principle, we expect that the rheological transitions (crossover between different rheological regimes) are determined by the coarse grained effective viscosity coefficients. The latter ones should be determined for the partially disordered (i.e., including defects) NTB phase flow.

BASIC DERIVATION OF THE NTB COARSE-GRAINED THEORY

The main feature which distinguishes the standard nematic N and the twist–bend nematic NTB liquid crystals is a short wavelength modulation of the orientation order φ presented in the NTB phase. This two component vector φ, orthogonal to the nematic director n (\(\boldsymbol{\varphi} \cdot \mathbf{n} = 0\)) can be chosen as the order parameter describing N–NTB phase transition. With this vector order parameter in hands one can write the Landau free energy functional.

Taking into account the nature of the short-scale vector field φ, we obtain (see more details in [22, 23])

$$\begin{gathered} \int dV\left\{ {\frac{a}{2}{{\boldsymbol{\varphi} }^{2}} + \frac{{{{b}_{3}}}}{{8q_{0}^{2}}}{{{\left[ {\left( {{{n}_{i}}{{n}_{k}}{{\partial }_{i}}{{\partial }_{k}} + q_{0}^{2}} \right)\boldsymbol{\varphi} } \right]}}^{2}} + \frac{{{{b}_{1}}}}{2}{{{(\nabla \boldsymbol{\varphi} )}}^{2}}} \right. \\ \left. { + \;\frac{{{{b}_{ \bot }}}}{2}\delta _{{ij}}^{ \bot }{{\partial }_{i}}\boldsymbol{\varphi} {{\partial }_{j}}\boldsymbol{\varphi} + \frac{\lambda }{{24}}{{\varphi }^{4}} - \frac{{{{\lambda }_{1}}}}{{16q_{0}^{2}}}{{{\left( {{{\epsilon }_{{ijk}}}{{\varphi }_{i}}{{\partial }_{j}}{{\varphi }_{k}}} \right)}}^{2}}} \right\}, \\ \end{gathered} $$
(1)

where \(\delta _{{ij}}^{ \bot } = {{\delta }_{{ij}}} - {{n}_{i}}{{n}_{j}}\). As usual, \(a \propto T - {{T}_{c}}\), where Tc is the mean field transition temperature. The quantities b are analogs of the Frank moduli for the order parameter φ. The free energy (1) represents the minimal Landau model for the N–NTB phase transition, neglecting fluctuations of the long-scale director n, which anyway is suppressed under shear (see, e.g., [24–26]). Then denoting a preferred direction, \({{{\mathbf{n}}}_{0}} = (0,0,1)\) we represent the Landau functional (1) in a more compact form by replacing the order parameter φ by its complex long- wavelength (!) counterpart ψ

$$\boldsymbol{\varphi} = 2{\kern 1pt} {\text{Re}}\left[ {\boldsymbol{\psi} \exp (i{{q}_{0}}z)} \right].$$
(2)

If \({{\lambda }_{1}} > 0\) then below the phase transition (at \(a < 0\)) minimization of the free energy leads to the conical helical structure with

$$\begin{gathered} {{\varphi }_{x}} = 2{\text{|}}{{\psi }_{x}}{\text{|}}\cos ({{q}_{0}}z + \theta ), \\ {{\varphi }_{y}} = \pm 2{\text{|}}{{\psi }_{x}}{\text{|}}\sin ({{q}_{0}}z + \theta ), \\ \end{gathered} $$
(3)

where θ is the phase of \({{\psi }_{x}} = \pm i{{\psi }_{y}}\) and signs ± correspond to two possible rotation directions of the conical structure.

It is worthwhile to mention the known in the literature other coarse grained descriptions of the NTB phase [27–29] (I sincerely thank the anonymous reviewer for attracting my attention to these works). Although the approaches [27–29] are conceptually similar to the model presented in this work, there is an essential difference. In our approach the long wavelength (nematic director) and short wavelength the NTB order parameter are explicitly separated into the Landau free energy expansion (1). Technically the short wavelength nature of the NTB order parameter yields to the specific form of the gradient terms, providing the softening of the order parameter in the vicinity of a circle in the reciprocal space (not around a single point (zero wave vector) as it is the case for the nematic order parameter). In the NTB phase but not too far from the transition point Tc (that is always the case due to (T – Tc)/Tc ≪ 1) the entering Landau theory (1) parameters \({{b}_{3}}\), \({{b}_{1}}\), \({{b}_{ \bot }}\), \(\lambda \), \({{\lambda }_{1}}\) and \({{q}_{0}}\) can be considered in the mean-field approximation as temperature independent, and only the controlling mean-field behavior coefficient a scales as T – Tc. Soft near the circle \({\text{|}}\mathbf{q}{\text{|}} = {{q}_{0}}\) in the reciprocal space fluctuations of the \({{{\text{N}}}_{{{\text{TB}}}}}\) order parameter changes this mean-field behavior (see more details below and also in [22]).

Since at the scales r larger than \(q_{0}^{{ - 1}}\) we are interested in this work, the NTB phase free energy and dynamic equations coincide with those for the effective smec-tic A, in what follows we will use interchangeably the both terms: NTB nematics when discussing generic features of the N → NTB phase transition, and effective smectic A, speaking about rheology.

Fluctuations around this mean-field state include long wavelength fluctuations

$$\mathbf{n} = {\mathbf{n}_{0}} + \delta \mathbf{n},$$
(4)

and short wavelength fluctuations φ which is orthogonal to n

$${{\boldsymbol{\varphi} }_{ \bot }} = 2{\text{Re}}\left[ {\boldsymbol{\psi} {{e}^{{i{{q}_{0}}z}}}} \right];\quad {{\varphi }_{{||}}} = - 2\delta \mathbf{n}{\text{Re}}\left[ {\boldsymbol{\psi} {{e}^{{i{{q}_{0}}z}}}} \right].$$
(5)

Two remarks are in order here. First, as it was shown previously [30–33] externally imposed shear flow suppresses long wavelength fluctuations. Second, renormalization group flow draws the system towards a symmetric state [34], therefore, the renormalized value of \({{b}_{1}}\) coefficient tends to zero. Then, the proposed (1) model is equivalent to the standard De Gennes model [24] describing nematic–smectic A phase transition [24, 35, 36]. It is worth to noting, that there is no density modulation in the liquid-like NTB phase. However, conical NTB orientation order, on scales much larger than the orientation modulation period looks like as a periodic in space layered smectic-like structure.

A wide range of coarse-grained models have been proposed, usually dedicated to modeling of multiscale systems. Coarse graining allows to decrease a number of essential degrees of freedom at the expense of microscopic details (e.g., replacing individual building blocks by their groups). Technically in this work we use slightly modified to be applicable to the NTB phase coarse-graining procedure described in [24] for the static behavior of cholesterics, and in [37] for dynamics of cholesteric liquid crystals. The properties of the deformed NTB liquid crystal depends essentially on the ratio of the inhomogeneity scale (say \({{r}_{{{\text{in}}}}}\)) and the NTB heliconical spiral pitch \(q_{0}^{{ - 1}}\). At scales \({{r}_{{{\text{in}}}}} \gg q_{0}^{{ - 1}}\) to find large-scale static and dynamic characteristics, we have to eliminate fast degrees of freedom. It is done [24, 37] by appropriate integration out the fast degrees of freedom. Performing the averaging we express the coarse grained coefficients (elastic moduli and viscosity coefficients) in terms of the bare NTB parameters defined at scales \( \ll {\kern 1pt} q_{0}^{{ - 1}}\).

The elastic energy of this coarse grained phase reads as

$$\tilde {F} = \frac{1}{2}\int {{d}^{3}}r\left[ {\tilde {B}{{{\left( {\frac{{\partial u}}{{\partial z}}} \right)}}^{2}} + \tilde {K}{{{\left( {\nabla _{ \bot }^{2}u} \right)}}^{2}}} \right].$$
(6)

Here u is layer displacement along the normal to the layer (z axis in our notation), and coarse-grained elastic moduli [24, 35] are

$$\tilde {B} = {{b}_{ \bot }}q_{0}^{2}{\kern 1pt} ;\quad \tilde {K} = \frac{3}{8}{{b}_{ \bot }}.$$
(7)

COARSE-GRAINED RHEOLOGY OF THE NTB PHASE

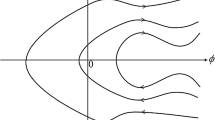
Since we are interested in rheological behavior (dynamics) the equilibrium elastic energy (6) should be supplemented by the coarse grained viscous (dissipative) stress tensor (see its derivation in [35, 37]). In what follows we consider two main rheological configurations (see Fig. 1) for the effective smectic, representing NTB nematic at large scales. Namely, perpendicular configuration (where the normal to the layer, unit vector l, perpendicular to the imposed shear velocity circulation curl v) and parallel configuration, where l parallel to curl v.

Fig. 1.
figure 1

Two rheological configurations considered in this work.

Full size image

It is worth to note that in the both configurations (l parallel to curl v, or l perpendicular to curl v) the shear velocity v is always oriented along the layers of the effective smectic.

Coarse grained (smectic-like) 5 viscosity coefficients [37] are expressed in terms of the bare (nematic-like). According to the definitions [27, 35] the uniaxial nematic phase N is characterized 5 independent viscosity coefficients \({{\eta }_{1}}{-} {{\eta }_{5}}\) (or 6 Leslie’s viscosity coefficients, which have to satisfied one constraint [24]). At small space scales (\(r < q_{0}^{{ - 1}}\)) these viscosity coefficients are certainly different in the N and \({{{\text{N}}}_{{{\text{TB}}}}}\) phases. However, the difference is relatively small (on the order of \({{\boldsymbol{\varphi} }^{2}}\)), and we neglect the difference in what follows. What is relevant for us is the fact that for two rheological configurations (see Fig. 1) we are interested in this work, only two combinations of the five viscosity coefficients are needed for a full description of dynamical behavior. The flow is determined by these two combinations of the coarse grained viscosity coefficients. Namely, \({{\tilde {\eta }}_{2}}\) coefficient determines the shear flow rheology for the perpendicular configuration, and the coarse grained viscosity \({{\tilde {\eta }}_{3}}\) determines the flow in the parallel configuration. It is worth to stress that coarse grained free energy of the NTB phase coincides with the smectic A free energy, provided the smectic layer displacement u is replaced by the phase of the NTB order parameter. Similar statements holds for the coarse grained dynamics of the NTB phase. However, we have to keep in mind that the coarse grained viscosity coefficients have a physical meaning only at the scales r larger than \(q_{0}^{{ - 1}}\). At smaller scales rheological behavior is determined by the bare viscosity coefficients. Therefore, when the shearing liquid crystal sample thickness becomes smaller than \(q_{0}^{{ - 1}}\) the coarse grained approximation is meaningless. In particularly no any room for the coarse grained theory in the N phase, where the NTB order parameter \({\text{|}}\boldsymbol{\varphi} {\text{|}} \to 0\) and hence \({{q}_{0}} \equiv 0\).

In the rheological configurations shown in Fig. 1 these two coarse grained viscosity coefficients can be expressed [37] in terms of the bare NTB viscosity coefficients (\({{\eta }_{i}}\), with \(i = 1,...,5\)) as

$${{\tilde {\eta }}_{2}} = 2{{\eta }_{2}} - \frac{1}{2}{{\eta }_{3}} + \frac{1}{4}{{\eta }_{1}};\quad {\kern 1pt} {{\tilde {\eta }}_{3}} = \frac{1}{4}\left[ {2{{\eta }_{3}} + 2{{\eta }_{2}} - {{\eta }_{1}}} \right].$$
(8)

For typical in nematic liquid crystals values of the bare viscosity coefficients [24–26], we estimate from (8) the values of the needed for us coarse grained bare viscosity coefficients:

$$\tilde {\eta }_{2}^{0} \simeq 0.832\;{\text{Poise}};\quad \tilde {\eta }_{3}^{0} \simeq 0.2\;{\text{Poise}}.$$
(9)

Because in the limit \(\dot {\gamma } \to 0\), \({{\tilde {\eta }}_{2}} > {{\tilde {\eta }}_{3}}\) just the perpendicular configuration is preferable one (the configuration leads to the maximum rate for the entropy production).

This principle (the maximum entropy production rate) as well as the apparently controversial statement (the principle of minimum entropy production) in each particular condition should be reconsidered, based on statistical mechanics, and hydrodynamics to find a stationary state for non-equilibrium systems. In this work we rely on the mapping of coarse grained dynamics of the NTB phase into that for the smectic A liquid crystals. With this mapping in hands the three regimes observed in the sheared NTB liquid crystals can be rationalized similarly to the known for smectic A results (see, e.g., two reviews [38, 39]), and the results suggest three rheological regimes which are governed by the maximum entropy production rate (irrespective to physical mechanisms behind).

To find the rheological relation for such configuration, and then the rheological phase diagram, one has to analyze the effective smectic order parameter fluctuations, and how the fluctuations are affected by the imposed shear \(\dot {\gamma }\). Our approach is more intuitive and qualitative than just solving the dynamical equations with imposed shear [30–33]. However, we expect that it will be useful, offering a deeper insight into physics behind the NTB phase rheology.

Our theory predictions are based on the following observations. The shear viscosity in the perpendicular configuration \({{\tilde {\eta }}_{2}}\) scales proportional to the correlation length [26]:

$${{\tilde {\eta }}_{2}} \propto \xi .$$
(10)

To proceed further with the rheological relation, we have to find how ξ scales with the shear rate \(\dot {\gamma }\). According to the Landau–Brazovskii weak crystallization theory (see original work [40], on thermodynamics and review [41], which includes also dynamics of the weak-crystallization transition), the correlation length scales as:

$$\xi \propto {{\Delta }^{{1/2}}},$$
(11)

where Δ is the gap in the soft mode, describing weak first order transition with emerging one, two, or three dimensional translational ordering. Said above leads to the following static correlation function for the order parameter [40]:

$$\frac{T}{{\Delta + \alpha {{{(q - {{q}_{0}})}}^{2}}}},$$
(12)

where α is a phenomenological coefficient translated into the elastic modulus below phase transition point. This form (12) of the correlation function is a specific feature of the weak crystallization transitions, where the critical mode softening occurs at the finite wave vector \({{q}_{0}}\). In dynamics [41] the dynamic response function corresponding to the presented above (12) correlation function reads as:

$$\frac{T}{{\omega - i[\Delta + \alpha {{{(q - {{q}_{0}})}}^{2}}]}}.$$
(13)

We see from (13) that Δ scales as the frequency ω, and therefore in the shear rheology condition as the shear rate \(\dot {\gamma }\). Finally combining everything together (11)–(13) we conclude that in a low shear rate:

$${{\tilde {\eta }}_{2}} \propto {{(\dot {\gamma })}^{{ - 1/2}}},$$
(14)

in the agreement with experimental data [20, 21]. Now we are in the position to estimate the first threshold value \({{\dot {\gamma }}_{{c1}}}\) for the shear rate. This threshold corresponds to the condition when \({{\tilde {\eta }}_{2}}\) becomes on the order of the bare value of \(\tilde {\eta }_{3}^{0}\):

$${{\dot {\gamma }}_{{c1}}} \propto {{\left( {\frac{{\tilde {\eta }_{2}^{0}}}{{\tilde {\eta }_{3}^{0}}}} \right)}^{2}}.$$
(15)

At the shear rate larger than the threshold \(\dot {\gamma } > {{\dot {\gamma }}_{{c1}}}\) a part of the NTB sample converts into the parallel configuration. Then, similar to the famous van-der-Waals–Maxwell construction [42, 43], the rheological curve corresponds to a sort of plateau. The plateau holds until when the entire volume of the NTB phase transforms into the parallel configuration. In the parallel configuration according to [26] \({{\tilde {\eta }}_{3}} \propto {{\xi }^{{5/2}}}\), and therefore the weak crystallization theory [41] predicts \({{\tilde {\eta }}_{3}} \propto {{(\dot {\gamma })}^{{ - 5/4}}}\). With this scaling in hands we estimate the second shear rate threshold \({{\dot {\gamma }}_{{c2}}}\) as:

$${{\dot {\gamma }}_{{c2}}} \propto {{\left( {\frac{{\tilde {\eta }_{2}^{0}}}{{\tilde {\eta }_{3}^{0}}}} \right)}^{4}}.$$
(16)

Finally when the \({{{\text{N}}}_{{{\text{TB}}}}}\) sample transforms completely into the parallel configuration (i.e., at \(\dot {\gamma } > {{\dot {\gamma }}_{{c2}}}\)) we face to the situation discussed first long ago by De Gennes [44] (see also more details concerning smectics in the works [30–33]). Namely, a large shear rate \(\dot {\gamma } > {{\dot {\gamma }}_{{c2}}}\) suppresses the order parameter fluctuations. Then we expect \({{\tilde {\eta }}_{3}}\) is shear rate independent quantity and we have the Newtonian-like rheology. Thus our simple model qualitatively explains all three rheological regimes observed experimentally [20, 21] in the NTB phase.

OUTLOOK AND CONCLUSIONS

Recent progress in rheology of the NTB liquid crystals has led to a number of new and exciting experimental results [20, 21]. In this work, we propose a simple heuristic approach to rationalize these new experimental data.

The approach is based on the coarse grained dynamic description of the NTB phase, valid for the space scales larger than the pitch of the NTB heliconical structure. Such description supplemented by the semi-qualitative arguments, relayed on the maximum entropy production rate, is used to estimate critical shear rate magnitudes separating different rheological regimes. The corresponding thresholds are determined by the coarse grained viscosities of the system. In own turn the coarse grained parameters entering the theory are expressed in terms of local quantities of the bare nematic liquid crystal. The latter characteristics could be measured by X-ray, NMR or other basically local probes.

The key starting point of our approach is based on a simple observation that the anisotropic viscous properties of the liquid crystals introduce a host of novel phenomena in rheology. We find that at relatively low shear rate (\(\dot {\gamma } \leqslant {{\dot {\gamma }}_{{c1}}}\)) the stress tensor \(\sigma \) created by this shear strain, scales as \(\sigma \propto {{\dot {\gamma }}^{{1/2}}}\). Thus, the effective viscosity decreases with the shear rate (\(\eta \propto {{\dot {\gamma }}^{{ - 1/2}}}\)) manifesting so-called shear-thinning phenomenon. At intermediate shear rate \({{\dot {\gamma }}_{{c1}}} \leqslant \dot {\gamma } \leqslant {{\dot {\gamma }}_{{c2}}}\), σ is almost independent of \(\dot {\gamma }\) (a sort of plateau), and at large shear rate (\(\dot {\gamma } \geqslant {{\dot {\gamma }}_{{c2}}}\)), \(\sigma \propto \dot {\gamma }\), and it looks like Newtonian rheology. Within our theory the critical values of the shear rate scales as \({{\dot {\gamma }}_{{c1}}} \propto {{(\tilde {\eta }_{2}^{0}{\text{/}}\tilde {\eta }_{3}^{0})}^{2}}\), and \({{\dot {\gamma }}_{{c2}}} \propto {{(\tilde {\eta }_{2}^{0}{\text{/}}\tilde {\eta }_{3}^{0})}^{4}}\), respectively. Here \(\tilde {\eta }_{2}^{0}\) and \(\tilde {\eta }_{3}^{0}\) are bare coarse grained shear viscosity coefficients of the effective smectics equivalent to the NTB phase at large scales. Our mainly qualitative theory may not have the right numbers for the dynamic shear rate thresholds. However, theory predicts the right scaling laws observed in the experiments. Our consideration suggests that the described phenomena and mechanisms can bring about different rheological scenarios worthy of further studies. In this work we have only scratched the surface of this reach subject, focusing only on the simplest questions, which can be answered by calculations “on a back of the envelope.”

The main message of this work is that coarse grained dynamic description of the NTB phase allows to rationalized observed in the phase different rheological regimes. Such coarse grained description supplemented by qualitative arguments based on the maximum rate of entropy production principle, can be used to estimate the critical values of the shear rate separating these rheological regimes. The estimations made in this work are applicable to the shearing of well-ordered samples of the NTB phase. If it is not the case, defects (disclinations or domain walls) affect the rheology. However, relying on the maximum entropy production rate principle, we expect that the rheological transitions (crossover between different rheological regimes) are determined by the coarse grained effective viscosity coefficients. The latter ones should be determined for the partially disordered (i.e., including defects) NTB phase flow. Guided by the modest aim of this work, we present only scaling analysis of three regimes of a steady shear viscosity curve which is in qualitative agreement with previously reported observations [20, 21, 28]. Even more not all of the observed qualitative features of the rheological curves are reproduced in our approach. For example, there is no independent of shear rate plateau in the interval \({{\dot {\gamma }}_{{c1}}} \leqslant \dot {\gamma } \leqslant {{\dot {\gamma }}_{{c2}}}\). Instead of that \(\sigma \propto {{\dot {\gamma }}^{\alpha }}\), where the exponent \(\alpha \simeq 0.1\) is small but not zero. The matter is that the estimated thresholds of rheological curves assume a well-defined orientation of the director respective to the shear flow. Most probably it is not the case in mentioned above experimental works, especially in the regions of relatively small shear rates. However, the ordered, defects-free states can be achieved, e.g., by orienting liquid crystal external field. Such investigation is beyond the scope of this work, direct experimental measurements of the ordered NTB phase rheology is still a challenging task. I hope that this work will stimulate discussions on the intriguing and important issues of non-Newtonian rheology in liquid crystals.