1 INTRODUCTION

Dissipative optical solitons now attract great attention in studies of nonlinear processes [1–10]. They are of both fundamental and applied interest. The mutual compensation of the energy entering a nonlinear medium and irreversible energy losses can result in the formation of dissipative solitons under certain conditions. The energy can be fed by various methods, e.g., from a continuous external source or an external pulse source, which can excite the nonlinear medium to a nonequilibrium state. In the latter case, the stored energy can further ensure its supply for the formation of dissipative solitons. If the duration τp of a dissipative soliton and the observation time \(\Delta t\) exceed the characteristic relaxation times T2 and T1 of the dipole moment and populations of stationary states, the nonequilibrium medium after the passage of the soliton becomes thermodynamically equilibrium.

The condition T2 ≪ T1 is usually valid in solids. The ratio T2/T1 can vary from 10–2 to 10–5 [11]. Consequently, it is possible to ensure the interesting condition

$${{T}_{2}} < {{\tau }_{{\text{p}}}} \ll \Delta t \ll {{T}_{1}}.$$
(1)

Under this condition, the pulse entering the medium can induce the transition of the initially nonequilibrium medium to another nonequilibrium metastable state. This process is accompanied by the formation of localized soliton-like objects [9, 12, 13]. These objects were called incoherent solitons in [14, 15] and soliton-like structures and soliton-like objects in nonequilibrium dissipative media in [12, 13]. These localized objects are short-lived: their lifetime is always shorter than the relaxation time T1 according to condition (1). Therefore, these objects can be observed in media and at quantum transitions where the relaxation time T1 is long. The relaxation time T1 at low temperatures is: \({{T}_{1}} \sim \omega _{{{\text{tr}}}}^{{ - 3}}\), where ωtr is the transition frequency. Hence, it is necessary to use quantum transitions with low frequencies ωtr, e.g., electron vibrational (Raman) transitions corresponding to normal vibrational modes of molecules. The relaxation time T1 for these transitions is fairly long. In particular, the relaxation time of the populations of Raman sublevels in liquid nitrogen is 56 s [16]. This giant T1 value with a great margin satisfies inequalities (1). It is also important that Raman transitions are forbidden in the electron dipole approximation and are fundamentally two-photon.

When the spectrum of an optical pulse covers the forbidden electron vibrational transition at the frequency ωv, stimulated Raman self-scattering occurs [17, 18]. In this case, the carrier frequency of the pulse is continuously redshifted in proportion to the traveled distance. The authors of [19, 20] showed that this mechanism at sufficiently long distances can generate a single-cycle or even unipolar signal.

The nonlinear optics of unipolar signals in the 1970s was exclusively of theoretical interest [21, 22]. Many theoretical studies performed in this field from 1988 to 1995 and in the 2000s, (see, e.g., [23–31]) were stimulated by experimental achievements in the generation of nearly single-cycle pulses [32–34].

The nonlinear optics of unipolar pulses is currently under rapid development [35–45]. In particular, the propagation of both conservative and dissipative solitons is studied.

Stimulated Raman self-scattering processes, which promote the formation of unipolar signals, can be accompanied by irreversible losses of the pulse energy at other, e.g., electron optical, quantum transitions. This can lead to the formation of localized unipolar soliton-like objects at the initial nonequilibrium populations of vibrational sublevels of molecules under the dominance of stimulated Raman scattering processes. This work is devoted to the study of this problem.

2 BASIC EQUATIONS

The electric field E of an unipolar pulse with the duration τp propagating in the z direction in an isotropic insulator containing Raman-active molecules satisfies the wave equation

$$\frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} = \frac{{4\pi }}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}({{P}_{{\text{e}}}} + {{P}_{{\text{R}}}}).$$
(2)

Here, c is the speed of light in vacuum and Pe and PR are the polarization electron optical and Raman responses, respectively.

The duration τp ~ 10–13 s certainly satisfies the inequality

$${{\delta }_{1}} = ({{\omega }_{0}}{{\tau }_{{\text{p}}}}{{)}^{{ - 1}}} \ll 1,$$
(3)

where \({{\omega }_{0}} \sim {{10}^{{15}}}{\kern 1pt} \) s–1 is the characteristic frequency of electron optical transitions.

If the left inequality in Eq. (1) is satisfied, the polarization response of electron optical transition can be treated as linear in the electric field strength of the pulse and [13]

$${{P}_{{\text{e}}}} = \chi E - \eta \frac{{\partial E}}{{\partial t}}.$$
(4)

Here, χ and η are the noninertial and inertial components of the electric susceptibility of the medium, the latter being due to the phase relaxation of electron optical transitions. They can be estimated as [12, 13] \(\chi \sim 2{{d}^{2}}n{\text{/}}\hbar {{\omega }_{0}}\) and \(\eta \sim 8{{d}^{2}}n{\text{/}}(\hbar {{T}_{2}}\omega _{0}^{3}) \sim \chi {\text{/}}({{T}_{0}}\omega _{0}^{2})\), where d is the characteristic dipole moment of allowed transitions, n is the concentration of molecules responsible for the linear susceptibility χ, and ħ is the reduced Planck constant.

Under the described conditions, the populations of quantum levels involved in electron optical transitions hardly change and correspond to thermodynamic equilibrium of the electron optical subsystem.

The Raman polarization response is given by the standard expression [46]

$${{P}_{{\text{R}}}} = {{n}_{{\text{R}}}}\alpha {\kern 1pt} 'qE,$$
(5)

where \(\alpha {\kern 1pt} ' = (\partial \alpha {\text{/}}\partial q{{)}_{{q = 0}}}\), α is the electric polarizability of a Raman-active molecule, q is the displacement of atoms in the molecule from the equilibrium position, and nR is the concentration of Raman-active molecules.

The dynamic parameters of a Raman transition at the frequency ωv satisfy the well-known equations [46]

$$\frac{{{{\partial }^{2}}q}}{{\partial {{t}^{2}}}} + \omega _{{\text{v}}}^{2}q = - \frac{{\alpha {\kern 1pt} '}}{{2M}}{{E}^{2}}w,\quad \frac{{\partial w}}{{\partial t}} = \frac{{\alpha {\kern 1pt} '}}{{\hbar {{\omega }_{{\text{v}}}}}}{{E}^{2}}\frac{{\partial q}}{{\partial t}},$$
(6)

where w is the population difference between the excited and ground Raman sublevels (w = 1 and –1 if the excited and ground sublevels are populated, respectively), M is the reduced mass of the molecule, and the relaxation terms are neglected because the duration of the pulse is much shorter than the relaxation times T1R and T2R for the Raman transition. It is noteworthy that the ground Raman sublevel coincides with the ground electron level in the molecule.

The frequency ωv ~ 1012 s–1 and the characteristic durations τp taken above satisfy the inequality

$${{\delta }_{2}} = ({{\omega }_{{\text{v}}}}{{\tau }_{{\text{p}}}}{{)}^{2}} \ll 1.$$
(7)

The spectral width of the unipolar pulse is δω ~ 1/τp. Consequently, the inequality (7) should be considered as the condition mentioned above that the spectrum of the signal includes the Raman frequency. As a result, this inequality ensures the most favorable conditions for stimulated Raman self-scattering.

The second term on the left-hand side of the first equation in Eqs. (6) can be neglected under the condition (7). In this case, the solution of system (5) has the form [19, 20]

$$\frac{{\partial q}}{{\partial t}} = - {\text{sgn}}(\alpha {\kern 1pt} '){{w}_{{ - \infty }}}\sqrt {\frac{{\hbar {{\omega }_{{\text{v}}}}}}{{2M}}} \sin \theta ,\quad w = {{w}_{{ - \infty }}}\cos \theta ,$$
(8)

where

$$\theta = \kappa \int\limits_{ - \infty }^t {{E}^{2}}dt{\kern 1pt} ',$$
(9)

\({{w}_{{ - \infty }}}\) is the initial (at \(t = - \infty \)) population difference between Raman sublevels, and \(\kappa = \frac{{{\text{|}}\alpha {\kern 1pt} '{\text{|}}}}{{\sqrt {2M\hbar {{\omega }_{{\text{v}}}}} }}\).

Under the condition (7), the displacement q is negligibly small; i.e., q = 0 can be set with a high accuracy [19]. Then, according to Eqs. (5) and (8),

$$\frac{{\partial {{P}_{{\text{R}}}}}}{{\partial t}} \approx {{n}_{{\text{R}}}}\alpha {\kern 1pt} '\frac{{\partial q}}{{\partial t}}E = - {{w}_{{ - \infty }}}{{n}_{{\text{R}}}}{\text{|}}\alpha {\kern 1pt} '{\text{|}}\sqrt {\frac{{\hbar {{\omega }_{{\text{v}}}}}}{{2M}}} E\sin \theta .$$
(10)

The substitution of Eqs. (4) and (10) into Eq. (2) yields the equation

$$\begin{gathered} \frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} - \frac{{n_{0}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} \\ = - \frac{{4\pi }}{{{{c}^{2}}}}\frac{\partial }{{\partial t}}\left( {\eta \frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} + {{w}_{{ - \infty }}}{{n}_{{\text{R}}}}{\text{|}}\alpha {\kern 1pt} '{\text{|}}\sqrt {\frac{{\hbar {{\omega }_{{\text{v}}}}}}{{2M}}} \sin \theta } \right), \\ \end{gathered} $$
(11)

where \({{n}_{0}} = \sqrt {1 + 4\pi \chi } \) is the noninertial part of the refractive index of the medium.

The two terms on the right-hand side of Eq. (11) are proportional to small parameters \({{\delta }_{1}}\) and \({{\delta }_{2}}\). Under these conditions, the unidirectional propagation approximation for the pulse along the z axis at a velocity close to \(c{\text{/}}{{n}_{0}}\) is applicable [22, 24, 25, 27, 30]. In this approximation, Eq. (11) takes the form

$$\frac{{\partial E}}{{\partial z}} + \frac{{{{n}_{0}}}}{c}\frac{{\partial E}}{{\partial t}} = \mu E\sin \theta + D\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}},$$
(12)

where

$$D = \frac{{2\pi }}{{c{{n}_{0}}}}\eta ,\quad \mu = \frac{{2\pi }}{{c{{n}_{0}}}}{{w}_{{ - \infty }}}{{n}_{{\text{R}}}}{\text{|}}\alpha {\kern 1pt} '{\text{|}}\sqrt {\frac{{\hbar {{\omega }_{{\text{v}}}}}}{{2M}}} .$$
(13)

The last, diffusion, term on the right-hand side of Eq. (12) describes irreversible losses caused by phase relaxation on electron optical transitions. The first term describes a nonlocal nonlinear source caused by stimulated Raman self-scattering at the inverted initial populations \(({{w}_{{ - \infty }}} > 0)\) of Raman quantum sublevels. Because of this term, Eq. (12) does not meet the g-eneral electric area conservation rule: \({{S}_{E}} \equiv \int_{ - \infty }^{ + \infty } Edt\) = const [47]. However, this nonlinear diffusion term is relatively small in the approximation (7). Thus, the violation of the \({{S}_{E}} = {\text{const}}\) rule is a consequence of the taken approximation and does not mean a physical contradiction.

Multiplying Eq. (12) by E, using Eq. (9), and integrating with respect to t, we obtain

$$\begin{gathered} \frac{{\partial \theta }}{{\partial z}} + \frac{{{{n}_{0}}}}{c}\frac{{\partial \theta }}{{\partial t}} \\ = 4\mu {{\sin }^{2}}\frac{\theta }{2} + D\frac{{{{\partial }^{2}}\theta }}{{\partial {{t}^{2}}}} - 2D\int\limits_{ - \infty }^t {{\left( {\frac{\partial }{{\partial t{\kern 1pt} '}}\sqrt {\frac{{\partial \theta }}{{\partial t{\kern 1pt} '}}} } \right)}^{2}}dt{\kern 1pt} '. \\ \end{gathered} $$
(14)

Nonlinear integrodifferential equations (12) and (14) describe the propagation of the pulse in the medium of Raman-active molecules in the presence of irreversible losses to electron optical quantum transitions.

3 SOLITON SOLUTION AND ITS ANALYSIS

An exact nontrivial analytical solution of Eq. (14), as well as Eq. (12), can hardly be found. For this reason, an approximate soliton-like solution is sought. To this end, it is desirable to approximate sin2(θ/2) in Eq. (14) by an appropriate polynomial. A Taylor series near θ = 0 is inappropriate for this purpose because the angular range 0 ≤ θ ≤ 4π/3 is of interest, as will be shown below. In this range, the approximation sin2(θ/2) ≈ F(θ) = pθ2 – qθ3 can be used with the constants p and g to be determined from the two conditions: (i) the polynomial reaches a maximum at the point θm = π and (ii) this maximum is equal to unity. As a result, p = 3/π2 and q = 2/π3. The resulting approximation in the angular range 0 ≤ θ ≤ 4π/3 has the form

$$\mathop {\sin }\nolimits^2 \frac{\theta }{2} \approx F(\theta ) = \frac{3}{{{{\pi }^{2}}}}{{\theta }^{2}} - \frac{2}{{{{\pi }^{3}}}}{{\theta }^{3}}.$$
(15)

It is seen in Fig. 1 that the approximation (15) in the angular range 0 ≤ θ ≤ 4π/3 is quite satisfactory.

Fig. 1.
figure 1

(Solid line) sin2(θ/2) and (dashed line) \(F(\theta )\) curves given by Eq. (15) in the angular interval \(0 \leqslant \theta \leqslant 4\pi {\text{/}}3\).

Full size image

The substitution of Eq. (15) into Eq. (14) yields the equation

$$\begin{gathered} \frac{{\partial \theta }}{{\partial z}} + \frac{{{{n}_{0}}}}{c}\frac{{\partial \theta }}{{\partial t}} \\ = a{{\theta }^{2}} - b{{\theta }^{3}} + D\frac{{{{\partial }^{2}}\theta }}{{\partial {{t}^{2}}}} - 2D\int\limits_{ - \infty }^t {{\left( {\frac{\partial }{{\partial t{\kern 1pt} '}}\sqrt {\frac{{\partial \theta }}{{\partial t{\kern 1pt} '}}} } \right)}^{2}}dt{\kern 1pt} ', \\ \end{gathered} $$
(16)

where a = 12μ/π2 and b = 8μ/π3.

In the absence of the last, integral, term, Eq. (16) is a reaction–diffusion equation. However, this term is important and cannot be omitted.

With the method considered in [9], the stationary solution of Eq. (16) can be found in the form of a propagating pulse

$$\theta = \frac{{{{A}_{\infty }}}}{2}(1 + \tanh \xi ),$$
(17)

where \(\xi = \frac{{t - z{\text{/}}v}}{{{{\tau }_{{\text{p}}}}}}\),

$${{A}_{\infty }} = \frac{{4\pi }}{3},$$
(18)
$${{\tau }_{{\text{p}}}} = \sqrt {\frac{{3\pi D}}{{8\mu }}} ,$$
(19)
$$\frac{1}{v} = \frac{{{{n}_{0}}}}{c} - \sqrt {\frac{{8\mu D}}{{3\pi }}} .$$
(20)

In Eqs. (17)–(20), the above expressions for a and b are used.

The electric field of the unipolar soliton-like pulse is expressed from Eqs. (17), (18), and (9) in the form

$$E = \pm \sqrt {\frac{{2\pi }}{{3\kappa {{\tau }_{p}}}}} {\text{sech}}\xi .$$
(21)

Here, the constants τp and v are the duration and velocity of the pulse, respectively.

The substitution of Eq. (21) into the expression I = cE2/(4πn0) for the signal intensity gives

$$I = {{I}_{{\text{m}}}}{\text{sec}}{{{\text{h}}}^{2}}\xi ,$$
(22)

where

$${{I}_{{\text{m}}}} = \frac{c}{{6{{n}_{0}}\kappa {{\tau }_{p}}}}.$$
(23)

From Eqs. (8), (17), and (18), we obtain the expressions for the translational velocity V of atoms in molecules and the population difference between the Raman sublevels in the form

$$V = \frac{{\partial q}}{{\partial t}} = - {\text{sgn}}(\alpha {\kern 1pt} '){{V}_{m}}\sin \left[ {\frac{{2\pi }}{3}(1 + \tanh \xi )} \right],$$
(24)
$$w = {{w}_{{ - \infty }}}\cos \left[ {\frac{{2\pi }}{3}(1 + \tanh \xi )} \right],$$
(25)

where \({{V}_{m}} = {{w}_{{ - \infty }}}\sqrt {\hbar {{\omega }_{v}}{\text{/}}2M} \).

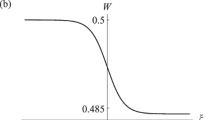
Figure 2 shows (a) the profile of the intensity (22) of the field of the unipolar pulse, as well as (b) the profile of the translational velocity of atoms (24) and (c) the profile of the population difference between the Raman sublevels (25), which are induced by this pulse.

Fig. 2.
figure 2

Profiles of (a) the intensity of the soliton pulse, (b) the translational velocity of atoms in molecules, and (c) the population difference between Raman sublevels.

Full size image

A horizontal plateau appears in the velocity profile immediately after the passage of the pulse; it is easily explained in terms of the first equation of the sys-tem (6). Indeed, the term \(\omega _{{\text{v}}}^{2}q\) (restoring force) is neglected in this equation under the condition (7). Then, this equation has the form \({{\partial }^{2}}q{\text{/}}\partial {{t}^{2}} = 0\), which gives the mentioned plateau \(V = {\text{const}}\). The lifetime of the plateau can be estimated as \(\omega _{{\text{v}}}^{{ - 1}}\). The term \(\omega _{v}^{2}q\) in the first equation of the system (6) becomes significant beginning with times \( \sim {\kern 1pt} \omega _{{\text{v}}}^{{ - 1}}\) after the passage of the pulse; this term is responsible for free oscillations corresponding to optical molecular modes.

In the absence of irreversible losses (for conservative solitons), the population difference w after the passage of the pulse returns to its initial value \({{w}_{{ - \infty }}}\) [25, 30]. As seen in Fig. 2, under the effect of irreversible phase relaxation in the system of electron optical transitions, the population difference \(w\) no longer returns to the initial value. In the central part of the pulse, Raman-excited molecules transit to the ground state. Immediately after the passage of the pulse in the medium, only about one-fourth of molecules on ave-rage return to the excited vibrational state. As a result, the average population difference becomes \({{w}_{{ + \infty }}} = - 0.5{{w}_{{ - \infty }}}\), which corresponds to another, metastable, state of molecules with the lifetime \( \sim {\kern 1pt} {{T}_{{1R}}}\). Thus, the pulse, transferring the most part of nonequilibrium Raman-active molecules to the ground Raman sublevel takes the energy \(0.5\hbar {{\omega }_{{\text{v}}}}{{n}_{{\text{R}}}}({{w}_{{ - \infty }}} - {{w}_{{ + \infty }}}) = \) \(0.75\hbar {{\omega }_{{\text{v}}}}{{n}_{{\text{R}}}}{{w}_{{ - \infty }}}\) from the unit volume of the medium. This energy income is compensated by losses caused by irreversible phase relaxation in the equilibrium system of electron optical transitions.

The energy of the pulse proportional to

$$A \equiv {{\theta }_{{t = + \infty }}} = \kappa \int\limits_{ - \infty }^{ + \infty } {{E}^{2}}dt$$
(26)

satisfies the equation (see Eq. (14) at \(t \to + \infty \))

$$\frac{{dA}}{{dz}} = 4\mu {{\sin }^{2}}\frac{A}{2} - 2D\int\limits_{ - \infty }^{ + \infty } {{\left( {\frac{\partial }{{\partial t}}\sqrt {\frac{{\partial \theta }}{{\partial t}}} } \right)}^{2}}dt.$$
(27)

Here, the first/second term corresponds to the energy supply to/loss from the pulse. The soliton-like object described above is due to the balance of these two processes.

The further analysis is performed with the approximation given by Eq. (15) and under the assumption of approximate self-similarity, i.e., under the assumption that θ is given by Eq. (17) with the substitution \({{A}_{\infty }} \to A(z)\), \(\xi \to \zeta = \frac{{t - f(z)}}{{{{\tau }_{0}}}}\), where \(f(z)\) is a certain function and τ0 is the duration of the pulse generally different from τp (see Eq. (19)). Summarizing, Eq. (27) is reduced to

$$\frac{{dA}}{{dz}} = \frac{{8\mu }}{{{{\pi }^{3}}}}Q(A),$$
(28)

where

$$Q(A) = - \frac{{9{{\pi }^{2}}\tau _{c}^{2}}}{{16\tau _{0}^{2}}}A + \frac{{3\pi }}{2}{{A}^{2}} - {{A}^{3}},$$
(29)
$${{\tau }_{{\text{c}}}} = \frac{2}{3}\sqrt {\frac{{\pi D}}{{3\mu }}} .$$
(30)

Figure 3 shows the plots of \(Q(A)\) at τ0 > τc and τ0 < τc. In the former case, the point A = A2 is an attractor if A > A1 at the entrance to the medium. Here,

$${{A}_{{1,2}}} = \frac{{3\pi }}{4}\left( {1 \mp \sqrt {1 - \frac{{\tau _{{\text{c}}}^{2}}}{{\tau _{0}^{2}}}} } \right).$$
(31)
Fig. 3.
figure 3

Plots of the cubic polynomial \(Q(A)\) at (thick line) τ0 > τc and (thin line) τ0 < τc.

Full size image

At A < A1, the point A = 0 is an attractor.

In the latter case (τ0 < τc), the point A = 0 is the only attractor. Thus, the found dissipative unipolar soliton-like object can be formed under two threshold conditions

$${{\tau }_{0}} > {{\tau }_{{\text{c}}}},\quad A > {{A}_{1}}.$$
(32)

These conditions are consistent with Eqs. (19) and (18), respectively, because τp > τc and \({{A}_{\infty }} > {{A}_{1}}\).

The substitution of τ0 = τp and Eq. (19) into Eq. (31) gives \({{A}_{1}} = \pi {\text{/}}6\) and \({{A}_{2}} = {{A}_{\infty }} = 4\pi {\text{/}}3\). Consequently, the point \({{A}_{\infty }}\) given by Eq. (18) is an attractor in this case at A > A1. This property is important evidence of the stability of the dissipative unipolar object under consideration.

Thus, the unipolar pulse satisfying the condi-tions (32) should be formed at the entrance to the Raman-active medium. Then, it can be transformed in the medium to the pulse with the duration, electric field strength, and intensities given by Eqs. (19)–(21), respectively. Numerous methods to generate unipolar electromagnetic signals are known (see, e.g., reviews [45, 48]). In our case, a significant part of the spectrum of the pulse with the duration τp ~ 10–13 s lies in the terahertz range. Consequently, this pulse can be referred to as a terahertz unipolar pulse. Such a pulse can be generated, e.g., by splitting of a bipolar terahertz signal into two unipolar pulses with opposite polarities [49]. One of these pulses under the conditions (32) can be used as an initial pulse at the entrance to the Raman-active medium.

Some numerical estimates are given below. For media with fast phase relaxation with the typical parameters [50] T2 ~ 10–13 s, \({{\omega }_{0}}\) ~ 1015 s–1, and χ ~ 0.1, we obtain \(\eta \sim \chi {\text{/}}({{T}_{2}}\omega _{0}^{2})\) ~ 10–18 s. Then, \(D = 2\pi \eta {\text{/}}c{{n}_{0}}\) ~ 10–27 s2/cm. Taking in addition \({\text{|}}\alpha {\kern 1pt} '{\text{|}}\;{{\sim }}\;{{10}^{{ - 15}}}\) cm2, \({{\omega }_{{\text{v}}}}\sim {{10}^{{12}}}\) s–1, \({{n}_{{\text{R}}}}\sim {{10}^{{21}}}\) cm–3, and \(M\sim {{10}^{{ - 22}}}{\kern 1pt} \) g [20], we find \(\mu = (2\pi {\text{/}}c){{n}_{{\text{R}}}}{\text{|}}\alpha {\kern 1pt} '{\text{|}}\sqrt {\hbar {{\omega }_{{\text{v}}}}{\text{/}}M} \sim 0.1\) cm–1. As a result, the duration of the dissipative soliton-like object is \({{\tau }_{{\text{p}}}}\sim \sqrt {D{\text{/}}\mu } \sim {{10}^{{ - 13}}}\) s, as expected above. The duration τp should be several times longer than the relaxation time T2 (see Eq. (1)). Note also that this duration of the pulse is much shorter than the phase relaxation time \({{T}_{{{\text{2R}}}}}\sim {{10}^{{ - 8}}}\) s [46] on the Raman transition in agreement with expectation.

The characteristic length of the pulse with the found duration τp in the propagation direction is l|| ~ cτp ~ 10–3 cm. The relative difference of the velocity of the pulse from \(c{\text{/}}{{n}_{0}}\) can be estimated as \({\text{|}}c{\text{/}}{{n}_{0}}v - 1{\text{|}}\;{{\sim }}\) \((c{\text{/}}{{n}_{0}})\sqrt {\mu D} \sim {{10}^{{ - 4}}}\) (see Eq. (20)). Thus, the velocity \(v\) of the soliton-like pulse only slightly differs from the linear velocity \(c{\text{/}}{{n}_{0}}\). With the above parameters, we have \(\kappa = {\text{|}}\alpha {\kern 1pt} '{\text{|/}}\sqrt {2M\hbar {{\omega }_{{\text{v}}}}} \sim {{10}^{4}}\) cm3/(erg s). Then, Eq. (23) gives the maximum intensity Im ~ 1012 W/cm2. Such high intensities are quite achievable in real experiments. The power of the pulse with the aperture dp ~ 1 mm is \(N\sim {{I}_{{\text{m}}}}d_{{\text{p}}}^{2}\sim {{10}^{{10}}}\) W, and its energy is W ~ Nτp ~ 1 mJ.

The above parameters satisfy the inequality l||  ≫ dp. The diffraction length under the considered conditions is estimated as \({{l}_{{\text{d}}}}\sim d_{{\text{p}}}^{2}{\text{/}}{{l}_{\parallel }}\sim 10\) cm. The one-dimensional approximation under consideration can be used at these distances. Then, the observation time of the process under study is estimated as \(\Delta t\sim {{l}_{{\text{d}}}}{\text{/}}c\sim {{10}^{{ - 9}}}\) s. This estimate, as well as the estimates presented above for τp and T2, certainly satisfies the condition (1).

4 CONCLUSIONS

To summarize, it has been shown that dissipative unipolar soliton pulses can be formed at the inverted initial populations of Raman sublevels. It is important that irreversible losses in the system of Raman sublevels are negligibly low at the taken observation time. These losses caused by phase relaxation are significant on other quantum transitions, e.g., electron optical transitions with the equilibrium populations of quantum states. The mutual compensation of these losses and the energy transferred from the nonequilibrium Raman subsystem makes it possible to form soliton-like pulses.

Since Raman enhancement is nonlinear, the dissipative soliton-like object is formed under the threshold conditions (32). At the same time, the initial state of the medium and its final metastable state to which it transits after the passage of the pulse are relatively stable because the expected observation time of the process of propagation of pulses is much shorter than the irreversible relaxation times in the system of Raman sublevels.

In agreement with expectation, such parameters of the considered dissipative object such as the amplitude, duration, and velocity are unambiguously determined by the characteristics of the medium. At the same time, these parameters are independent of the characteristics of the pulse at the entrance to the medium. This property is common for dissipative solitons and is confirmed by the fact that the pulse seemingly “forgets” its parameters at the entrance to the medium because of irreversible losses. This situation is similar to the limit cycle in the theory of self-oscillations.

The approximate solution Eq. (14) has been obtained in the approximation (15), which is satisfied with a high accuracy in the interval \(0 < \theta < 4\pi {\text{/}}3\). In this case, \({{A}_{\infty }} = 4\pi {\text{/}}3\). As a result, other solutions for which \(\theta \) values leave this interval most probably remain unfound. The amplitude, duration, and velocity of such pulses will likely have another set of values. In any case, this set should be fixed for a soliton-like pulse with a certain parameter \({{A}_{\infty }}\). This is consistent with the property of the parameters of dissipative solitons, in contrast to conservative solitons, to take discrete sets of values [1]. I am going to study this issue separately in application to solutions of Eq. (14) (see also Eq. (12)).