Lattice Dynamics of Bi₂Те₃ and Vibrational Modes in Raman Scattering of Topological Insulators MnBi₂Te₄·n(Bi₂Te₃)

This work is devoted to the experimental study and symmetry analysis of the Raman-active vibration modes in MnBi₂Te₄·n(Bi₂Te₃) van der Waals topological insulators, where n is the number of Te–Bi–Te–Bi–Te quintuple layers between two neighboring Te–Bi–Te–Mn–Te–Bi–Te septuple layers. Confocal Raman spectroscopy is applied to study Raman spectra of crystal structures with $n = 0,1,2,3,4,5,6$, and ∞. The experimental frequencies of vibration modes of the same symmetry in the structures with different n are compared. The lattice dynamics of free-standing one, three, and four quintuple layers, as well as of bulk Bi₂Те₃ $(n = \infty )$ and MnBi₂Te₄ $(n = 0)$, is considered theoretically. Vibrational modes of the last two systems have the same symmetry, but different displacement fields. These fields in the case of a Raman-active mode do not contain displacements of manganese atoms for any finite $n$. It is shown that two vibrational modes in the low-frequency region of the spectrum (35–70 cm^–1) of structures with $n = 1,\;2,\;3,\;4,\;5$, and 6 practically correspond to the lattice dynamics of n free quintuple Bi₂Те₃ layers. For this reason, the remaining two vibration modes, which are observed in the high-frequency region of the spectrum (100–140 cm^–1) and are experimentally indistinguishable in the sense of belonging to quintuple or septuple layer or to both layers simultaneously, should also be assigned to vibrations in quintuple layers under immobile atoms of septuple layers.

1 INTRODUCTION

Prior to the discovery of the first intrinsic antiferromagnetic topological insulator MnBi₂Te₄ with a Néel temperature of 25.4 K [1], various possibilities were considered to create a magnetic gap at the Dirac point of a topological insulator (TI) and to obtain the phase of the quantum anomalous Hall effect (QAHE). The simplest way to solve the problem was implemented both theoretically [2, 3] and experimentally [4] by doping a nonmagnetic TI with magnetic atoms. However, since the distribution of magnetic atoms in real TIs is nonuniform, the magnetic gap varied irregularly along the surface [5], which caused too low a temperature of the QAHE. Another method based on the so-called magnetic proximity effect near the TI/ferromagnetic semiconductor interface generally shifts the topological surface state deeper into the TI and, correspondingly, weakens the magnetic effect [6, 7]. The above drawbacks can be overcome to a large extent by depositing an ultrathin ferromagnetic insulator film on the surface of the nonmagnetic TI provided that the crystal structure and atomic composition of the former are close to those of the latter [6, 8–11]. The appearance of MnBi₂Te₄ largely removed the problem of creating a magnetic gap in the spectrum of topological surface states and, at the same time, gave rise to the start of research on a whole series of crystalline analogs of MnBi₂Te₄, known today as MnBi₂Te₄·n(Bi₂Te₃), where n is the number of the quintuple Te–Bi–Te–Bi–Te atomic layers (QLs) between the neighboring septuple Te–Bi–Te–Mn–Te–Bi–Te atomic layers (SLs) in a structure with a given n value [12].

The importance of studying this series as natural heterostructures was first emphasized in study [13] of topological surface states and magnetic and transport properties of MnBi₂Te₄·n(Bi₂Te₃) and, later, was underlined in [12, 14–24], including studies of Raman scattering [12, 19–24]. However, lattice dynamics, as well as other properties of structures with n > 3, still remains unexplored. A significant discrepancy between the number of Raman-active modes which should be observed according to the symmetry analysis of a bulk crystal and that of the modes found in Raman spectra of the structures with $n = 1$, 2, and 3 is also still unexplained. It should be noted that, although the MnBi₂Te₄·n(Bi₂Te₃) structures at room temperature are paramagnetic, their topology is also nontrivial [25, 26].

In this work, we report Raman studies for MnBi₂Te₄·n(Bi₂Te₃) topological insulators with $n = 0,1, \ldots ,6,\infty$. In addition, the lattice dynamics of one, three, and four Bi₂Те₃ QLs, as well as bulk Bi₂Те₃ ($n = \infty$) and MnBi₂Te₄ ($n = 0$), is studied theoretically. The overall results obtained make it possible to establish a very unusual lattice dynamics of topologically nontrivial MnBi₂Te₄·n(Bi₂Te₃) systems and to explain the aforementioned discrepancy.

2 SAMPLE PREPARATION AND X-RAY ANALYSIS

Single-phase samples of each member of the series were cleaved under an optical microscope from MnBi₂Te₄·n(Bi₂Te₃) crystalline ingots grown by the Bridgman–Stockbarger method from preliminarily synthesized polycrystalline phases of each composition. The synthesis procedure and growth conditions differed from those for MnBi₂Te₄ [12] only by the percentage of the initial components and a small change in the growth temperature, in accordance with the required $n$ values. Diffraction patterns from $(000l)$ planes confirming the compliance of the structure of each of the studied samples with the required $n$ values were obtained using a Bruker XRD D2 Phaser X-ray diffractometer (Cu ${{K}_{{\alpha 1}}}$ radiation; 5° ≤ 2θ ≤ 100°). The phase composition was determined and the structural analysis of the samples was carried out using the EVA and TOPAS-4.2 software packages. Structural data obtained for all members of the series are shown in Table 1.

Table 1. Space group symmetry, lattice parameters, and sequence of alternation of quintuple (5) and septuple (7) layers for each member of the MnBi₂Te₄·n(Bi₂Te₃) series

3 METHODOLOGY OF EXPERIMENTAL AND THEORETICAL STUDIES OF RAMAN SCATTERING

Raman scattering was studied using a Nanofinder 30 confocal setup (Tokyo Instruments, Japan) with a diffraction grating of 1800 lines/mm and a spectral resolution of 0.5 cm^–1. Scattering was excited at a wavelength of 532 nm by the second harmonic of a Nd:YAG laser with a maximum power of 10 mW. The diameter of the laser spot on the sample did not exceed 4 μm. The signal was detected in the photon count mode by a CCD camera cooled to a temperature of ‒100°C. The signal collection time interval did not exceed 1 min, and the signal itself was filtered out using LP03-532RU-50 edge filters (Semrock Company). The filter location (https://www.semrock.com/filter-spectra-at-non-normal-angles-of-incidence.aspx) made it possible to record 100% of the Raman signal in the spectral range of 40–5000 cm^–1 and at least 50% of the signal in the spectral range of 35–40 cm^–1. The measurements were carried out in the backscattering geometry. The spectra are presented in the work in the normalized form.

Theoretical calculations were carried out within the density functional perturbation theory. In the case of MnBi₂Te₄, the pseudopotential method was used within the ABINIT code [27] in the basis of plane waves. In the case of Bi₂Te₃, we used a pseudopotential approach and a mixed basis [28, 29], in which the valence states are presented as a combination of plane waves and local s and p orbitals at Bi and Te nodes, which made it possible to reduce the cutoff energy for plane waves to 10 Ry without loss of accuracy. The PBE approximation [30] was used for the exchange-correlation functional. All calculated values were obtained taking into account the spin–orbit coupling [31]. When integrating over the Brillouin zone, we used 96 × 96 and 12 × 12 inhomogeneous k-point grids near the center of the Brillouin zone (for small k values) and for the rest of the Brillouin zone, respectively.

The complete vibrational representation for all members of the MnBi₂Te₄·n(Bi₂Te₃) series is given in Table 2.

Table 2. Complete vibrational representation for each member of the MnBi₂Te₄·n(Bi₂Te₃) series; N is the number of atoms in a unit cell. The group-theory notation of each representation at the Γ point is given in parentheses after the spectroscopic notation (center of the Brillouin zone). Vibrations ${{E}_{u}}$ and ${{E}_{g}}$ are doubly degenerate

4 RESULTS AND DISCUSSION

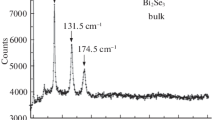
Compounds with $n = \infty$ and $n = 0$ are end members of the MnBi₂Te₄·n(Bi₂Te₃) series and their structures contain only QLs and only SLs, respectively (Table 1, last column). The Raman spectra of these members are shown in Fig. 1.

Fig. 1.

(Color online) Frequencies and symmetry of Raman phonon modes observed in (pink line) MnBi₂Te₄ and (blue line) Bi₂Te₃.

The mode identification for MnBi₂Te₄ (Fig. 1, pink line) is based on the comparison of the experimental spectra with the calculated phonon frequencies and symmetry at the Γ point (Fig. 2) and is in agreement with the data recently obtained in [24], where the polarization of the observed phonons was additionally measured. For Bi₂Te₃ (Fig. 1, blue line), the observed modes are identified by comparison with the calculated frequencies and mode symmetries shown in Fig. 3.

Fig. 2.

(Color online) Displacement fields of Raman-active vibration modes in MnBi₂Te₄. Observed/calculated frequencies in inverse centimeters are given at the bottom of each mode.

Fig. 3.

(Color online) Displacement fields of Raman-active vibration modes of Bi₂Te₃. Observed/calculated frequencies in inverse centimeters are given at the bottom of each mode.

It can be seen in Figs. 2 and 3 that the displacement fields for the modes with the same symmetry in MnBi₂Te₄ and Bi₂Te₃, as well as in all other members of the series, are different. In both figures, the horizontal displacements of atoms occur in the plane of the layers, while the vertical displacements are perpendicular to this plane. For simplicity, only the directions of displacement of each atom are indicated. Manganese atoms are not involved in Raman-active vibrations.

As seen in Table 2, six and four modes are expected in the Raman spectra of MnBi₂Te₄·n(Bi₂Te₃) with $n = 0$ (MnBi₂Te₄) and $n = \infty$ (Bi₂Te₃), respectively. In the spectra shown in Fig. 2, only five of six and three of four expected Raman modes are observed, respectively. As follows from the data in Fig. 1 and Table 2, the missing mode for each material is the mode with the ${{E}_{g}}$ symmetry.

The observation of this low-frequency Raman mode in the bulk Bi₂Te₃ sample is complicated by instrumental limitations (see the preceding section) and becomes impossible at a certain signal intensity. At least, this mode was not observed in [32–37]. At the same time, the observation of a mode with the ${{E}_{g}}$ symmetry and a frequency of 36.5 cm^–1 in Bi₂Te₃ was reported in [38–41]. In MnBi₂Te₄, the low-frequency ${{E}_{g}}$ mode with a calculated frequency of 28.2 cm^–1 (Fig. 2, $E_{g}^{1}$) has not yet been observed in any published works. Therefore, in further discussions, we use the calculated value of the frequency of this mode.

Figure 4 shows the Raman spectra of all members of the MnBi₂Te₄·n(Bi₂Te₃) series. As follows from this figure, the most significant difference is observed between the spectra of MnBi₂Te₄ $(n = 0)$ and MnBi₄Te₇ $(n = 1)$.

Fig. 4.

Evolution of Raman spectra in MnBi₂Te₄·n(Bi₂Te₃) with the variation of $n$. Dashed lines 1, 3, 5, and 6 connect modes of the same symmetry and cross the lower and upper horizontal axes as follows: (1) 38 and 41 cm^–1, (3) 57.4 and 61 cm^–1, (5) 101 and 101 cm^–1, and (6) 139 and 133 cm^–1, respectively. Dashed lines 2 and 4 cross the lower horizontal axis at 45.8 and 65.4 cm^–1, respectively. (The 110 cm^–1 mode in MnBi₂Te₄ is not shown in Fig. 4.)

The spectra of MnBi₄Te₇ and MnBi₂Te₄ are presented in Fig. 5 (black circles) along with their decomposition into components (solid green lines).

Fig. 5.

(Color online) Data obtained in this work for the structures with n = (upper spectrum) 1 and (lower spectrum) 0. The results of decomposition of the spectra into components are shown by green solid lines. The vertical dashed line marks the calculated position of the lowest frequency mode $E_{g}^{1}$ in MnBi₂Te₄ [12].

Let us compare the lowest frequency modes $(E_{g}^{1},A_{{1g}}^{1})$ of MnBi₂Te₄ (Fig. 2) and Bi₂Te₃ (Fig. 3) with in-phase displacements of Bi and Te atoms with the lowest frequency modes in the spectra of MnBi₄Te₇ and MnBi₂Te₄ (Fig. 5, top and bottom spectra, respectively), which are also easily identified as the $E_{g}^{1}$ and $A_{{1g}}^{1}$ modes.

In MnBi₄Te₇, these modes are blueshifted (by more than 20%) compared to MnBi₂Te₄. Such a significant increase in frequency when replacing one MnBi₂Te₄ SL by one Bi₂Te₃ QL is clearly associated with a decrease in the number of atoms involved in in-phase displacements, which takes place upon transition from MnBi₂Te₄ to Bi₂Te₃ (cf. the $E_{g}^{1}$ and $A_{{1g}}^{1}$ modes in Figs. 2 and 3).

The decomposition of the spectra into components (Fig. 5, solid green lines) indicates that the number of modes observed for MnBi₄Te₇ is clearly less than that for MnBi₂Te₄, contrary to expectations. At the same time, any additional broadening of the fundamental modes caused by the increased number of atoms in the unit cell of MnBi₄Te₇ and the increased number of modes is absent (Table 2, second and fourth columns, respectively). The superposition of such modes with close frequencies should lead to the broadening of the main lines. According to the decomposition and the analysis of the broadening of the constituent components for all spectra in Fig. 4, the spectra of all MnBi₂Te₄·n(Bi₂Te₃) with n ≥ 1 contain four modes. It is noteworthy that the number of modes for MnBi₄Te₇ and MnBi₁₄Te₂₂ could reach 12 and 36, respectively (see data for n = 1 and 6 in the fourth column of Table 2, respectively).

Thus, while the number of modes in the experimental spectra of MnBi₂Te₄ completely agrees with the data of the symmetry analysis for a bulk crystal, their number in MnBi₂Te₄·n(Bi₂Te₃) with $n > 0$ at first glance contradicts these data. This contradiction is removed if we assume that the vibrational modes in MnBi₂Te₄·n(Bi₂Te₃) with $n > 0$ are completely or almost completely frequency degenerate.

The low-frequency $E_{g}^{1}$ and $A_{{1g}}^{1}$ modes in MnBi₂Te₄·n(Bi₂Te₃) with $n > 0$ correspond to $E_{g}^{1}$ and $A_{{1g}}^{1}$ vibrations of $n$ Bi₂Te₃ QLs, which agrees with our calculations carried out selectively for one, three, and four Bi₂Te₃ QLs and given in Table 3.

Table 3. (Second to fifth columns) Observed and (seventh to tenth columns) calculated frequencies of Raman-active vibrational modes for different numbers of quintuple layers in MnBi₂Te₄ ·n(Bi₂Te₃)

In fact, it can be seen in Table 3 that the calculated frequencies of these modes for one Bi₂Te₃ QL almost coincide with the observed frequencies of the modes with a similar symmetry in MnBi₂Te₄·n(Bi₂Te₃) with $n = 1$. The frequencies of these modes tend to increase with an increase in the number of Bi₂Te₃ QLs from 1 to 4, similar to that observed for low-frequency modes in MnBi₂Te₄·n(Bi₂Te₃) when $n$ varies from 1 to 4 (Fig. 4).

Thus, the overall data obtained for vibrational modes indicate that a part of the lattice dynamics of MnBi₂Te₄·n(Bi₂Te₃) with $n > 0$ associated at least with low-frequency Raman modes is determined by the lattice dynamics of n Bi₂Te₃ QLs.

This is in good agreement with the experimental data for Raman scattering in ultrathin Bi₂Te₃ films grown by the gas transport method on Si/SiO₂ or fluorphlogopite mica substrates [41]. Similar to the low-frequency ${{E}_{g}}$ mode in MnBi₂Te₄·n(Bi₂Te₃) with $n > 0$, the low-frequency ${{E}_{g}}$ mode was observed for two Bi₂Te₃ QLs (the minimum number of QLs studied in [41]) and its intensity dropped rapidly with a further increase in the number of QLs. The difference of ~2 cm^–1 between the frequencies of this mode in MnBi₂Te₄·n(Bi₂Te₃) with n = 2 (Table 3, 38.5 cm^–1) and two Bi₂Te₃ QLs (36.5 cm^–1 [37]) is apparently caused by a technological factor. In the former case, the substrate needed to obtain one (two, etc.) Bi₂Te₃ QLs (the second case) is absent, and the resulting structure is free of its influence. The same as for MnBi₂Te₄·n(Bi₂Te₃) with $n > 0$, in the case of one or more Bi₂Te₃ layers, the low-frequency ${{A}_{{1g}}}$ mode is slightly blueshifted with an increase in the number of Bi₂Te₃ QLs. Our data for MnBi₂Te₄·n(Bi₂Te₃) with nonzero n are given in Fig. 6 in comparison with the data from [41] for Bi₂Te₃ with different numbers of QLs. It is clearly seen that the effect of the substrate, which is noticeable for the case $n = 2$, decreases rapidly with increasing n and almost vanishes for $n > 3$.

Fig. 6.

(Solid lines) Data obtained in this work for MnBi₂Te₄ ·n(Bi₂Te₃) with $n = 2,3,4,5,6$, and ∞ and (circles) data obtained in [41] for bulk Bi₂Te₃ and two (2QL), three (3QL), four (4QL), five (5QL), six (6QL) quintuple layers of Bi₂Te₃.

According to the calculations (Table 3, ninth column), the high-frequency ${{E}_{g}}$ mode in Bi₂Te₃ does not experience frequency dispersion upon change in the number of Bi₂Te₃ QLs in much the same way as similar modes in MnBi₂Te₄·n(Bi₂Te₃) in Fig. 4, the frequency of which (101 cm^–1) does not change with increasing $n$. Although the frequencies of the E_g modes connected by vertical dashed line 5 in Fig. 4 are the same (101 cm^–1), these modes cannot be considered as identical or be attributed to vibrations associated with MnBi₂Te₄ SLs or Bi₂Te₃ QLs in MnBi₄Te₇. These modes are indistinguishable in the experimental data obtained.

A similar situation is observed for the highest frequency ${{A}_{{1g}}}$ mode in Bi₂Te₃ (Table 3, tenth column), and for similar modes in Fig. 4. High-frequency modes that have the same ${{A}_{{1g}}}$ symmetry but different frequencies of 139 (MnBi₂Te₄) and 136 cm^–1 (MnBi₄Te₇) and are connected by vertical dashed line 6 in Fig. 4 also cannot strictly speaking be attributed to MnBi₂Te₄ SLs or Bi₂Te₃ QLs or to both simultaneously. A slight (2%) decrease in the frequency of this high-frequency mode at the appearance of one Bi₂Te₃ QL in MnBi₂Te₄ $(n = 0)$ and the formation of MnBi₄Te₇ $(n = 1)$ cannot be decisive for choosing any one of the above options for belonging to this mode. Nevertheless, the presence of low-frequency modes associated with vibrations in quintuple layers also requires the appearance of high-frequency modes of these layers. For this reason, high-frequency modes also have to be attributed to the vibrations of Bi and Te atoms in quintuple layers under stationary atoms in septuple layers. The same is required by the passage to the limit to the spectrum of Bi₂Te₃, which would otherwise be impossible.

5 CONCLUSIONS

Raman-active vibrational modes of the MnBi₂Te₄·n(Bi₂Te₃) system with $n > 0$ in the studied region of the spectrum are almost completely frequency degenerate. As a consequence, the number of observed modes is limited and equals four as for Bi₂Te₃. The degeneracy covers both low-frequency modes with in-phase displacements of atoms and high-frequency modes with out-of-phase displacements of atoms. In both cases, the vibrational modes correspond to the displacements of the Bi and Te atoms in quintuple layers, while the atoms of septuple layers are completely or almost immobile. Note that the immobility of the Bi and Te atoms in septuple layers is in no way caused by the symmetry restrictions, as in the case of the central Mn, which is not involved in Raman-active vibrations in MnBi₂Te₄·n(Bi₂Te₃) with any n because of the symmetry of its position.

In general, an interesting situation is implemented in which septuple layers of MnBi₂Te₄ are almost “silent,” but this silence is not due to symmetry and is not related to the so-called silent modes that are inactive both in Raman scattering and in infrared reflection (absorption) and have nonzero displacements of atoms. We are unaware of examples of such behavior of vibrational modes in layered crystals.

The absence of the contribution of magnetic Mn atoms to the Raman spectra of lattice vibrations indicates the need for studies of infrared spectra of MnBi₂Te₄·n(Bi₂Te₃) According to our estimates, the upper limit of the frequencies of dipole vibrations involving Mn is approximately 200 cm^–1.

In the context of this work, which is based on data obtained at room temperature, there is no connection between vibrational modes and magnetic phase tr-ansitions. However, such a connection can be revealed in low-temperature studies of the entire MnBi₂Te₄·n(Bi₂Te₃) series, and the data of this work will serve as a starting point for the analysis of the results obtained. We have already started work in this direction.