INTRODUCTION

There is a growing interest in the spin of particles as a highly sensitive spin resonance detector of cosmic axions and axion-like particles. Axions, first proposed by Peccei and Quinn in 1977 [1] as a solution to strong CP-violation in QCD, are widely discussed as a pl-ausible candidate for the dark matter. One of manifestations of the cold galactic halo axions will be a NMR‑like resonant rotation of the spin in the oscillating axion field [2–6]. Here the spin serves as an axion antenna and the experimental search by the JEDI collaboration of the axion signal with polarized deuterons in the storage ring COSY is in progress [7]. Since the axion mass is unknown, one is bound to spin precession frequency scanning. In the JEDI experiment one looks for a buildup of the vertical polarization from the idly precessing in-plane polarization when the resonance condition is met during a scan.

Inherent to the JEDI technique is a need for a long coherence time of the in-plane precessing spin. For instance, it cannot be easily extended to protons with arguably short spin coherence time. Besides that, the axion signal depends on the unknown difference of phases of the axion field and idle spin precession. In this communication we suggest the alternative scheme which is free of these limitations and looks preferred one for searches for axions at the Nuclotron, NICA [8], and PTR [9] storage rings. All one needs is an internal polarimetry which both the Nuclotron and NICA proper will be equipped with, and there is no need in the rf spin rotators. We also comment on exclusive features of the spin frequency scan in hybrid rings with concurrent electric and magnetic bending, the PRT storage ring proposed by the CPEDM collaboration being a good example.

A comprehensive introduction into the physics of axions is found in reviews [4, 10–12], here we only mention the principal points of importance to our discussion, alongside the basics of the spin precession in storage rings [10–15]. When the angular frequency of the axion field is about three times the expansion rate of the Universe, coherent oscillations of the cold cosmological axion field do establish [16–18]. Attributing the local energy density of the dark matter \({{\rho }_{{{\text{DM}}}}} \approx \) 400 MeV/cm3 [19] to axions in the invisible halo of our Galaxy, the amplitude of the classical axion field \(a(x) = {{a}_{0}}\cos \left( {{{\omega }_{a}}t - {{{\mathbf{k}}}_{a}} \cdot {\mathbf{x}}} \right)\) can be evaluated as [2, 20]

$${{a}_{0}} = \frac{1}{{{{m}_{a}}}}\sqrt {\frac{{2{{\rho }_{{{\text{DM}}}}}\hbar }}{{{{c}^{3}}}}} .$$
(1)

Of key importance is Weinberg’s gradient interaction of axions with fermions [21],

$${{L}_{{a\bar {\psi }\psi }}} = - \frac{1}{{2{{f}_{a}}}}{{g}_{f}}\overline \psi {{\gamma }^{\mu }}{{\gamma }_{5}}\psi {{\partial }_{\mu }}a(x),$$
(2)

which can be reinterpreted as an interaction of fermion’s spin with the pseudomagnetic field [22]. The dimensionless constant \({{g}_{f}} \sim 1\) depends on the specific model, and Weinberg derived the relation,

$${{m}_{a}} \approx {{m}_{\pi }}\frac{{{{f}_{\pi }}}}{{{{f}_{a}}}}\frac{{\sqrt {{{m}_{u}}{{m}_{d}}} }}{{{{m}_{u}} + {{m}_{d}}}}{\kern 1pt} ,$$
(3)

where \({{m}_{\pi }}\) and \({{f}_{\pi }}\) are the pion mass and decay constant, respectively, and \({{m}_{{u,d}}}\) are mases of light quarks. Still another manifestation of the galactic axion field is the oscillating contribution to the electric dipole moment (EDM) of nucleons [2, 23],

$$\begin{array}{*{20}{l}} {d_{N}^{{{\text{ax}}}}(x) = \frac{{a(x)}}{{{{f}_{a}}}}\frac{{{{\mu }_{N}}}}{c}{{\kappa }_{a}},} \end{array}$$
(4)

where \({{\mu }_{N}}\) is the nuclear magneton and the small factor

$$\begin{array}{*{20}{l}} {{{\kappa }_{a}} \sim \frac{{{{m}_{d}}{{m}_{u}}}}{{{{\Lambda }_{{{\text{QCD}}}}}({{m}_{d}} + {{m}_{u}})}} \approx {{{10}}^{{ - 2}}}} \end{array},$$
(5)

describes the chiral suppression of the EDM by small masses of light quarks [24, 25].

We consider storage rings with crossed magnetic and electric bending fields. The cyclotron angular velocity equals

$${\mathbf{\Omega }_{c}} = \frac{q}{{m\gamma }}\left( { - {\mathbf{B}} + \frac{{{\mathbf{v}} \times {\mathbf{E}}}}{{{{v}^{2}}}}} \right){\kern 1pt} .$$
(6)

The contributions to the spin rotation with respect to the particle momentum, \({\mathbf{\Omega }_{s}} = \mathbf{\Omega } _{s}^{{{\text{mdm}}}} + \mathbf{\Omega } _{s}^{{{\text{edm}}}}\), due to the particle’s magnetic dipole moment (MDM), \(\mu = g{{\mu }_{N}}\), and the electric dipole moment (EDM), d, is given by the generalized BMT equations [15–17]:

$$\mathbf{\Omega } _{s}^{{{\text{mdm}}}} = \frac{q}{m}\left\{ { - {\kern 1pt} G{\kern 1pt} {\mathbf{B}} + \left( {G - \frac{1}{{{{\gamma }^{2}} - 1}}} \right)\frac{{{\mathbf{v}} \times {\mathbf{E}}}}{{{{c}^{2}}}}} \right\}{\kern 1pt} ,$$
(7)
$$\mathbf{\Omega } _{s}^{{{\text{edm}}}} = - d\{ {\mathbf{E}} + {\mathbf{v}} \times {\mathbf{B}}\} {\kern 1pt} .$$
(8)

Here, \(G = (g - 2){\text{/}}2\) is the magnetic anomaly, v and γ are particle’s velocity and the relativistic γ-factor, and the spin tune, \({{\nu }_{s}}\), is defined via \(\mathbf{\Omega } _{s}^{{{\text{mdm}}}} = {{\nu }_{s}}{{\Omega }_{c}}\).

AXION EFFECTS IN ALL MAGNETIC RINGS

We consider first all magnetic storage rings, \({\mathbf{E}} = 0\), when \({{\nu }_{s}} = G\gamma \). The salient features of spin as an axion antenna are as follows. First of all, in the comoving frame (cmf) the axion field induced EDM interacts with the motional electric field

$${{{\mathbf{E}}}_{{{\text{cmf}}}}} = [{\mathbf{v}} \times {\mathbf{B}}] = - (m\gamma {\text{/}}q) \cdot [{\mathbf{v}} \times {\mathbf{\Omega }_{c}}]{\kern 1pt} .$$
(9)

As a spin rotator, it is tantamount to the radiofrequency Wien filter [26] with the radial magnetic field, operated at the axion field angular velocity

$${{\omega }_{a}} = \frac{{{{m}_{a}}{{c}^{2}}}}{\hbar }{\kern 1pt} .$$
(10)

Secondly, spin interacts with the oscillating pseudomagnetic field, proportional to the particle velocity and the time derivative \({{\partial }_{t}}a(x)\) [22], tangential to the particle orbit and acting as an rf solenoid. Finally, the velocity of particles in a storage ring, \(v\), is of the order of the velocity of light and \(v \approx {{10}^{3}}{{v}_{a}}\), where \({{v}_{a}}\sim \) 250 km/s is the velocity of Earth’s motion in the Galaxy. Hence the pseudomagnetic field acting on the spin of stored particles is three orders in magnitude stronger compared to that acting on, for instance, the spin of ultracold neutrons [27, 28].

At the axion resonance \({{\omega }_{a}} = {{\nu }_{s}}{{\Omega }_{c}}\), and the instantaneous angular velocity of the axion-driven resonant spin rotation, derived by Silenko [28], takes the form

$$\begin{gathered} {\mathbf{\Omega }_{{{\text{res}}}}} = \frac{{{{a}_{0}}}}{{{{f}_{a}}}}{\kern 1pt} \left( {{{g}_{f}}{{\omega }_{a}}\sin ({{\omega }_{a}}t)\frac{{\mathbf{v}}}{c}} \right. \\ - \;{{\kappa }_{a}}\gamma \cos ({{\omega }_{a}}t)\left. {\left[ {\frac{{\mathbf{v}}}{c} \times {\mathbf{\Omega }_{c}}} \right]} \right). \\ \end{gathered} $$
(11)

The phases of two spin rotators differ by \(\pi {\text{/}}2\), but they do rotate spin about orthogonal axes. Hence upon solving the generalized BMT equations by the Bogo-liubov–Krylov averaging [29, 30], one finds the angular velocity of the resonant up–down rotation of the spin envelope

$${{\Omega }_{{{\text{res}}}}} = \frac{{{{a}_{0}}}}{{2{{f}_{a}}}}{\kern 1pt} \frac{{\gamma v}}{c}{\text{|}}{{g}_{f}}G - {{\kappa }_{a}}{\text{|}}{{\Omega }_{c}}{\kern 1pt} .$$
(12)

Note a strong enhancement of the contribution from the pseudomagnetic field by the factor \({{g}_{f}}G{\text{/}}{{\kappa }_{a}} \gg 1\) compared to the contribution from the axion driven EDM. In the early simulations of operation of the storage-ring spin antenna as an axion detector, the contribution of this pseudomagnetic field was not taken into account in [7] and the actual sensitivity of the JEDI experiment was greatly underestimated.

FREQUENCY SCAN SEARCH FOR THE AXION SIGNAL

From now on we focus on the case of the initial vertical polarization \({{P}_{y}}\). At a fixed \({{\omega }_{a}}\), we parameterize a variation of the spin precession angular velocity as \({{\Omega }_{s}}(t) = {{\omega }_{a}} + 2\Omega _{t}^{2}t\), where \(2\Omega _{t}^{2} = d{{\Omega }_{s}}{\text{/}}dt\). Our convention for time is such that a scan starts at negative time \(t = - {{t}_{0}}\) and the exact resonance takes place at \(t = 0\). The spin phase during the scan varies as

$${{\theta }_{s}}(t) = {{\omega }_{a}}t + \Omega _{t}^{2}{{t}^{2}},$$
(13)

and duration of the scan is such that \(\Omega _{t}^{2}t_{0}^{2} \gg 2\pi \). A sensitivity to weak axion signal depends on the relationship between the spin coherence time, \({{\tau }_{{SCT}}} = 1{\text{/}}\Gamma \), and the speed of the spin precession frequency scan. Specifically, it is easy to derive the time dependence of the axion-driven in-plane polarization envelope \({{P}_{{xz}}}\):

$${P}_{xz}(t) = {P}_{y}{\Omega }_{\text{res}} \int\limits_{ - {t}_{0}}^t d\tau \exp \left[ { - \Gamma (t - \tau )} \right]\cos (\Omega _{t}^{2}{\tau }^{2}){\kern 1pt} .$$
(14)

In the usually discussed scheme with the in-plane initial polarization [6, 7, 31, 32], the axion signal will be proportional to \(\sin \Delta \) [29, 33], where Δ is an entirely unknown difference of the spin precession and axion oscillation phases. As a practical remedy, it was proposed to fill the ring with four bunches of different polarizations [6, 7]. In contrast to that, a buildup of the in-plane polarization from the initial vertical one is free of this phase ambiguity.

Numerical evaluation of the integral (14) is not a problem, here we proceed to simple analytic evaluations, leaving aside the issue of numerical simulations. First, we start with the limit of large spin coherence time, \(\Gamma \ll {{\Omega }_{t}}\), when the exponential damping factor in the integrand can be neglected, what is the case for stored deuterons. Then the envelope \({{P}_{{xz}}}\) will exhibit a jump of temporal width \({{t}_{1}} \sim 1{\text{/}}{{\Omega }_{t}}\) and the amplitude \(P_{{xz}}^{{\max }} \sim {{P}_{y}}{{\Omega }_{{{\text{res}}}}}{\text{/}}{{\Omega }_{t}}\). The observed signal will be a jump in the up-down asymmetry in the polarimeter oscillating with the spin precession frequency. A Fourier analysis technique for extraction of the spin envelope form such an asymmetry data has been developed by the JEDI collaboration [34, 35].

The opposite limiting case of \(\Gamma \gg {{\Omega }_{t}}\) is of interest for stored protons which, because of the large magnetic anomaly, will arguably have a short spin coherence time [36]. Here emerges a new time scale

$${{t}_{2}} \sim \frac{\Gamma }{{\Omega _{t}^{2}}}{\kern 1pt} .$$
(15)

Algebraically at times \( - {{t}_{2}} < t < {{t}_{2}}\) the envelope \({{P}_{{xz}}}\) will oscillate with constant amplitude,

$${{P}_{{x,z}}} \approx \frac{{{{\Omega }_{{{\text{res}}}}}}}{\Gamma }{{P}_{y}}\cos (\Omega _{t}^{2}{{t}^{2}}){\kern 1pt} ,$$
(16)

while oscillations will vanish beyond this interval. The practical Fourier analysis of the up-down asymmetry from the in-plane precessing polarization returns the envelope as a positive defined quantity, and the axion signal will look like a corrugated plateau of the height \({\text{|}}{{P}_{{xz}}}{\text{|}} \sim {{\Omega }_{{{\text{res}}}}}{\text{/}}\Gamma \) and width \({{t}_{2}}\).

A lesson from searches for resonances is that at similar statistics broad resonances are much harder to be identified. However, in our case a salient feature of the signal (16) is a central peak of width \( \sim {\kern 1pt} 1{\text{/}}{{\Omega }_{t}}\), the peaks at wings will have a spacing \( \sim {\kern 1pt} {{\tau }_{{SCT}}}\) and can be resolved if sufficient statistics can be accumulated during the spin coherence time. Fits to the well specified function (16) will facilitate identification of the axion signal. Furthermore, the central peak will be better visible at faster ramping of the cyclotron frequency such that

$$\frac{{d{{\Omega }_{c}}}}{{dt}} \sim {{\Gamma }^{2}}{\kern 1pt} .$$
(17)

Still another option is to run the proton ring at magic energies with strong suppression of the spin decoherence as was suggested in [36]. These magic energies are roots of the equation

$$\begin{array}{*{20}{l}} {1 - \frac{{{{c}^{2}}}}{{{{v}^{2}}}}\left( {1 + \frac{K}{{G\gamma }}} \right)\left( {\frac{1}{{\gamma _{{tr}}^{2}}} - \frac{1}{{{{\gamma }^{2}}}}} \right) = 0,\quad K = \pm 1, \pm 2,...} \end{array}$$
(18)

exact position of magic energies depends on the transition γ-factor, \({{\gamma }_{{tr}}}\), of the particular ring. For instance, at COSY the roots exist at negative K. The lowest magic kinetic energy for protons is \({{T}_{p}} \approx 30\) MeV at \(K = - 2\), and as an axion antenna it will be tuned to search for axions with \({{\omega }_{a}} = (2 - {{G}_{p}}){{\Omega }_{c}}\), where \({{G}_{p}} = 1.793\) is the magnetic anomaly of the proton. The next magic energy at \(K = - 3\) is \({{T}_{p}} \approx 130\) MeV, and the COSY will be tuned to \({{\omega }_{a}} = (3 - {{G}_{p}}){{\Omega }_{c}}\). At still higher magic energy \({{T}_{p}} \approx 210\) MeV one will probe \({{\omega }_{a}} = (4 - {{G}_{p}}){{\Omega }_{c}}\). Note that \({{\Omega }_{c}}\) scales with \( \propto {\kern 1pt} \gamma {\text{/}}\sqrt {{{\gamma }^{2}} - 1} \).

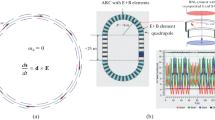
AXION EFFECTS IN HYBRID STORAGE RINGS

Note that in all magnetic fields the resonance condition entails \({{\omega }_{a}} = p{\text{/}}(R\gamma m)\), where R is the ring radius and p is the particle momentum. Consequently, as an axion antenna the attainable axion masses are bounded from below by the minimal momentum the storage ring can run at. The hybrid ring with concurrent magnetic and electric bendings are much more versatile compared to all magnetic rings. An example is provided by the prototype test ring PTR proposed by the CPEDM collaboration [9]. With the radial electric field \({{E}_{0}} = 7 \times {{10}^{6}}\) V/m complemented by the vertical magnetic field \({{B}_{0}} = 0.0327\)T, PTR will provide the frozen spin of protons, \(\mathbf{\Omega } _{s}^{{{\text{mdm}}}} = 0\); i.e., \({{\nu }_{s}} = 0\). Beyond this point, the electric and magnetic fields must be varied synchronously to preserve the injection energy, the orbit radius and the cyclotron frequency,

$$\Delta {\mathbf{B}} = \frac{1}{{{{v}^{2}}}}[{\mathbf{v}} \times \Delta {\mathbf{E}}]{\kern 1pt} ,$$
(19)

see Eq. (6). Then according to Eq. (7) the spin tune will vary as

$${{\nu }_{s}} = - {{G}_{p}}\gamma \frac{{\Delta E}}{{{{E}_{0}}}}{\kern 1pt} ,$$
(20)

taking the canonical value, \({{\nu }_{s}} = G\gamma \), in the all-magnetic limit of \(\Delta E = - {{E}_{0}}\). In the same range the magnetic field must be raised concurrently to

$$B = \frac{{{{G}_{p}} + 1}}{{1 - {{G}_{p}}{{\gamma }^{2}}{{\beta }^{2}}}}{{B}_{0}} = 3.39{{B}_{0}}{\kern 1pt} .$$
(21)

The practically attainable range of magnetic fields will depend on the design of the air coil. We emphasize that arguably the spin coherence time \({{\tau }_{{SCT}}}\) scales with \(1{\text{/}}\nu _{s}^{2}\) [36], which specifically favors operation of the hybrid PTR as an axion antenna to search for small mass axions.

Note that at the fixed orbit of the beam the electric field in the comoving frame, acting on proton’s EDM, does not depend on \(\Delta E\), while the axion resonance will take place at

$${{\omega }_{a}} = - {{G}_{p}}\gamma {{\Omega }_{c}}\frac{{\Delta E}}{{{{E}_{0}}}}{\kern 1pt} .$$
(22)

The resulting angular velocity of the axion-driven spin rotation will be given by

$${{\Omega }_{{{\text{res}}}}} = \frac{{{{a}_{0}}}}{{2{{f}_{a}}}}\frac{{\gamma v}}{c}{\text{|}}{{g}_{f}}G\frac{{\Delta E}}{{{{E}_{0}}}} + {{\kappa }_{a}}{\text{|}}{{\Omega }_{c}},$$
(23)

with the pseudomagnetic field contribution suppressed by the factor \(\Delta E{\text{/}}{{E}_{0}}\). Increasing the electric field in detectors must be viewed impractical.

A hybrid storage ring operating as a broadband axion antenna at a fixed beam energy has several advantages. We mention injection at a fixed energy, running the radiofrequency cavity in a narrow range of frequencies, a polarimetry optimized for one fixed energy.

SUMMARY

It has been demonstrated how the spin of polarized protons can be used as an axion antenna in spite of the short spin coherence time of the in-plane polarization of protons. The key point is to look for a buildup of the idly precessing in-plane polarization starting from the stable vertical one. Of special interest is a possibility to enhance a sensitivity to axions working at selected beam energies with strong suppression of spin decoherence effects. Hybrid prototype rings emerge as a promising proton spin antenna sensitive to axions with small masses up to a few nanoelectronvolts per the square of speed of light. These observations suggest new options for the experimental searches for axions at NICA in Dubna, COSY in Juelich, planned PTR and elsewhere. We emphasize that our approach can readily be extended to the hybrid deuteron storage rings.