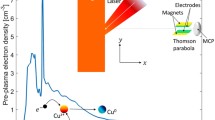
A method has been proposed to increase the rate of loading of atoms in a U-magneto-optical trap near an atom chip. The method is based on the focusing of a slow atomic beam into the localization region of the atom chip. The overdamped focusing regime has been considered. In this case, the focal length is independent of the initial transverse velocity of atoms. It has been shown that the focusing of the atomic beam makes it possible to increase the loading rate in the localization region 250 μm in diameter by a factor of 160.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 INTRODUCTION
Localized atoms are used in many precise atomic interferometry experiments. The development of this trend has already resulted in the creation of a new generation of sensors, quantum sensors based on the measurement of the effect of physical fields on quantum degrees of freedom of atoms. Quantum sensors provide an accuracy higher than that of existing classical sensors. Sensors based on atomic interferometry for measuring inertial forces [1, 2], including gravimeters [2, 3], gradiometers [4, 5], and gyroscopes [6] belong to the most developed quantum sensors. The accuracy of modern atom gravimeters and gradiometers already exceeds the accuracy of many classical analogs [7], and their application demonstrates a high reliability [8–12].
Atomic clocks and frequency standards constitute another type of quantum sensors based on atomic interferometry [13, 14]. The application of localized atoms allows one to create compact systems that can be used on board aircraft. The demonstrated stability of such clocks [15] allows them to increase the accuracy of existing onboard systems through the use of cold atoms.
The decisive parameters of quantum sensors affecting their accuracy and convenient application are the number and temperature of cooled atoms, spatial dimensions of the atomic ensemble, and measurement time. Modern quantum sensors operate in a periodic regime, which is determined by the periodic regime of the formation of the cold atomic ensemble: cooling of thermal atoms, their localization, additional cooling in an atom trap, optical pumping to a certain magnetic sublevel, and the interaction of the prepared atomic ensemble with a given sequence of laser (in the case of the gravimeter and gradiometer) or microwave (in the case of atomic clocks) pulses. The total measurement time depends on the operating time at each stage of the experimental sequence. The critical parameters are the cooling rate of thermal atoms and the formation time of the primary ensemble of cold atoms localized in the magneto-optical trap. This stage is the longest and determines the acquisition time of data measured by a quantum sensor. The reduction of the cooling time of atoms in the magneto-optical trap decreases the total number of atoms, which finally increases noise of the signal measured by the quantum sensor.
The development of quantum sensors involving atom chips has recently begun. This approach allows one to increase the degree of control at the preparation of the primary atomic ensemble used to measure physical fields. The atom chip technology will make it possible to create compact atomic clocks with an accuracy exceeding existing compact clocks. These clocks can be established on board aircraft. We have recently demonstrated a single-layer atom chip [16], which can serve as a start platform for high-precision quantum sensors. The main advantage of the described approach is the possibility of continuous cooling of atoms in the magneto-optical trap using only currents flowing in microwires of the atom chip in the presence of a uniform external magnetic field. However, the number of atoms that can be localized near such a chip is limited by the deviation of the magnetic field in the localization region from an ideal quadrupole field in the magneto-optical trap [17–19]. The aim of this work is to study the possibility of using the focusing of the atomic beam into the localization region in order to increase the number of localized atoms.
2 LOADING OF ATOMS INTO THE MAGNETO-OPTICAL TRAP
The variation of the number of atoms in the magneto-optical trap (MOT) is described by the expression [20]
where N is the number of atoms in the magneto-optical trap, R is the loading rate of atoms, τ is the lifetime of atoms in the MOT, and βc is the coefficient characterizing losses of the trap at binary collisions of atoms inside the trap. The first term describes the loading rate of atoms into the MOT, the second term represents loss of atoms and is usually determined by collisions of atoms with the residual gas in the vacuum chamber, and the third term describes losses in binary collisions, which also limit the maximum density in the MOT at a value of \(n\sim \) 1010 atoms/cm3. The maximum number of atoms that can be localized is given by the expression [20]
This expression is valid when the third term in Eq. (1) can be neglected. According to Eq. (2), to increase the number of atoms localized in the MOT (in any considered approximation), it is necessary either to increase the efficiency of loading or to reduce collisional losses of localized atoms with the residual gas in the chamber. The latter is reached by increasing the efficiency of vacuum system pumping. The w-orking pressure of residual gases in the chamber at the creation of quantum sensors is currently about 10‒10 Torr. Such an ultrahigh vacuum is also necessary for the operation with atoms in the Bose–Einstein condensate. A further improvement of vacuum is a complex and expensive problem and makes the creation of mobile quantum sensors problematic.
Another way to increase the number of localized atoms in the MOT is the increase in the loading rate R. This parameter in classical three-dimensional MOTs, where the magnetic field is formed by two macroscopic coils in the anti-Helmholtz configuration, is proportional to the size of laser beams [21, 22]. This occurs because the quadrupole field of macroscopic coils of the MOT allows efficient cooling at any point of the laser beam. In fact, the trapping region of atoms in this case is determined by the size of laser beams.
The situation with the atom chip is different. An analog of the MOT near the atom chip is a U-trap (Fig. 1). This trap is based on the magnetic field generated by a current flowing in a U-microwire together with an external uniform magnetic field [23]. Since the shape of the atom chip limits the penetration of the laser field to the localization region of atoms, a different configuration of the laser field involving the mirror MOT is used. In the mirror MOT, one of the cooling beams propagates along the surface of the atom chip and the second beam is reflected from it at an angle of 45°. This configuration of laser fields is equivalent to the configuration used in the classical MOT, and it could be expected that the loading rate of atoms into the U-MOT will also be determined by the size of laser beams, but this is not the case. The main problem of loading of the U-MOT is the deviation of the magnetic field distribution from the quadrupole field, which is implemented when two coils in the anti-Helmholtz configuration are used [17]. To create the U-MOT on the atom chip, it is necessary to use thin wires; as a result, the magnetic field distribution differs from the quadrupole one and, thereby, limits the cooling volume of atoms. In this case, the cooling rate is determined by the size of the magnetic field region where atoms are cooled rather than by the size of laser beams.
There are several approaches to solve the problem of efficient loading of atoms into the U‑MOT. The most widespread approach based on an increase in the width of the central part of the U-wire [17–19] was used by several research groups [24], which used wide macrowires to create the magnetic field of the atom chip for the primary cooling of atoms near the atom chip. Such macrowires are located under the main atom chip and are used for several aims. First, they can conduct high currents without significant heating. This in turn allows one to increase the time necessary for the cooling of atoms. Second, the potential of such a trap is closer to the required potential in the quadrupole magnetic field.
An alternative approach to increase the width of the microwire is based on the use of several microwires with different parameters and directions of currents [25]. This approach allows an additional possibility of optimization of the magnetic field distribution in the localization region of atoms. However, such a configuration is engineeringly complex. An intermediate MOT formed by magnetic coils in the mirror MOT configuration can also be used to efficiently load the potential of the U-MOT [26]. However, in this approach, magnetic coils should be placed in a small volume, which can be technically impossible.
Another approach is based on the use of preliminarily cooled atoms for loading. Indeed, the efficiency of loading depends not only on the volume where the conditions for cooling and localization are optimal but also on the phase-space density of atoms that can be localized in the U-MOT. The deviation of the magnetic field from the ideal one limits the maximum possible velocity of atoms from which they can be cooled and localized. Preliminary cooling allows one to increase the number of low-velocity atoms, which ensures their efficient loading to the U-MOT.
A possible variant of using preliminary cooling is the loading of atoms from the precooled atomic beam. This approach is widely used to load not only atom chips [24] but also classical three-dimensional MOTs [27]. The atomic beam can be preliminarily cooled with a Zeeman slower as, e.g., in [27]. However, such an approach is not necessarily convenient. Another approach involves sources of atoms forming cold beams such as the two-dimensional (2D) MOT [28], 2D+ MOT [29], and low-velocity intense source (LVIS) of atoms [30]. These sources yield intense beams of cold atoms and are widely used to load atom chips [24].
One of the features of such systems is the formation of the atomic beam with a low longitudinal velocity [29]. Unfortunately, since the residual transverse velocity exists and the time of flight from the LVIS to the atom chip is long in this approach, the diameter of the atomic beam near the chip can increase to several millimeters because the longitudinal velocity is low. This circumstance is insignificant if the preliminary cooling and localization near the atom chip are ensured by the mirror or U-MOT formed by thick macrowires. In this case, the spatial size of the effective capture region of the MOT will be comparable with the size of the atomic beam. If the atom chip is loaded directly without additional magnetic coils and macrowires as, e.g., in [16], it is necessary to reduce the transverse velocities of the low-velocity beam.
3 FOCUSING OF THE ATOMIC BEAM
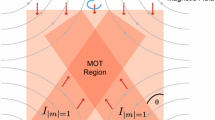
The transverse velocity of the atomic beam can be controlled by three methods. The first method is based on the formation of two-dimensional optical molasses on the way of propagation of the atomic beam [31]. This method makes it possible to collimate the atomic beam and to increase the atomic phase-space density. This in turn allows one to obtain a high atomic phase-space density in their localization region. The second method is based on the two-dimensional compression of the atomic beam in the two-dimensional magneto-optical trap [32]. This method of controlling the transverse velocity of the atomic beam is actively used to produce intense cold atomic beams [33]. The two-dimensional compression of the atomic beam can increase the density of cold atoms in the localization region of atoms on the atom chip. A disadvantage of this method is the necessity of high magnetic field gradients.
The third method based on the focusing of the atomic beam using the two-dimensional magneto-optical trap can be implemented at lower magnetic field gradients [34, 35]. It is a two-dimensional analog of the three-dimensional pulsed compression of the magneto-optical trap considered in [34]. The main feature of this method is that the focusing point of atoms in the beam in the longitudinal direction is independent of their transverse velocity because the atom in the field of the 2D MOT at the saturation of the atomic transition can be treated as an overdamped oscillator.
To estimate the applicability of this approach to increase the load rate of the MOT formed near the atom chip, we consider the interaction of the atom with the laser field in the presence of the magnetic field gradient. Because of symmetry, this problem can be considered for a one-dimensional magneto-optical trap (Fig. 2). The atomic beam is formed from the LVIS of atoms and propagates along the Z axis. The laser field is formed by two laser beams counterpropagating along the X axis that have the circular polarizations σ+ and σ– and the frequency detuning δ from the resonance of the atom at rest. The atom in the ground and excited states has the total angular momenta Fg = 0 and Fe = 1, respectively, and the resonant absorption line with the half-width γ (Fig. 3). Conductors with the current that are located along the Z axis generate the quadrupole field with the gradient along the X axis \(g = dB{\text{/}}dx\). The interaction region of the atom with laser radiation in the magnetic field has the length L, which is limited by the size of the laser beam in the real experiment. The interaction time of each atom moving at the velocity \({{v}_{z}}\) along the Z axis is \({{t}_{{{\text{int}}}}} = L{\text{/}}{{v}_{z}}\). The atom with the coordinate \(x\) in the interaction region is subjected to the light pressure force [36], which consists of two components F(ΔmF = –1) acting at the {Fg = 0, mF = 0} → {Fe = 1, mF = –1} transition and F(ΔmF = 1) acting at the {Fg = 0, mF = 0} → {Fe = 1, mF = 1} transition, where mF is the projection of the total angular momentum of the atom on the quantization axis. These forces are opposite because they are induced by the interaction of the atom with counterpropagating laser beams. The total force is
where \(\alpha = 2\pi \times 1.4{\kern 1pt} \) MHz/G is the Zeeman shift of the resonance absorption line in the magnetic field \({{B}_{x}} = gx\). As shown in [34], the focusing point in the used approximation is independent of the transverse velocity of the atom.
(Color online) Scheme of the energy levels of the atom in the magnetic field linearly varying along the X axis. The atom in the ground and excited states has the total angular momenta Fg = 0 and Fe = 1, respectively, and is placed in a laser field formed by two counterpropagating laser beams that have the circular polarizations σ+ and σ– and the frequency detuning δ from the resonance of the atom at rest.
Under the condition \(\delta \gg \alpha gx + k\dot {x}\) (which is valid for the atomic beam with low transverse velocities, which can be reached in the LVIS), the expression in parentheses can be expanded in a series. The transverse velocity \({{v}_{x}}\) of the atom flying through the interaction region with the laser beam can be determined from the Newton’s second law \(F = dp{\text{/}}dt\), where \(dp\) is the momentum change determined by the interaction time \({{t}_{{{\text{int}}}}}\) of the atom with laser radiation. Under the assumption that the X coordinate of the atom does not change during its interaction with laser radiation, we obtain
where \(m\) and \(v_{x}^{0}\) are the mass and initial transverse velocity of the atom, respectively. It is seen that \(\beta < 0\) at negative detunings and the atom in this case acquires an additional momentum directed toward the Z axis. The focal length of the atomic lens f can be defined as the distance from the two-dimensional MOT to the point of intersection of the atom with the Z axis.
According to Eq. (3), the transverse velocity of atoms after the interaction with the 2D MOT under the condition \({{t}_{{{\text{int}}}}} = L{\text{/}}{{v}_{z}} > {\text{|}}1{\text{/}}\beta {\text{|}}\) is independent of the initial transverse velocity. In this regime, atoms interact with the laser field as an overdamped oscillator. For this reason, the focal length is independent of the transverse velocity of the atom. Moreover, the exponential term in Eq. (3) can be neglected in this case (at a negative detuning of the laser frequency) and the transverse velocity is given by the expression
which gives the focal length
According to Eq. (4), the focal length depends on the longitudinal velocity of the atom and atoms with different velocities are focused at different distances from the lens. This property is similar to the chromatic aberration of the conventional lens. This effect can be used to monochromatize the atomic beam [35] and is negative for an increase in the efficiency of loading of the atom chip because it limits the focusing of atoms with different velocities in the localization region in the U-MOT.
The localization length of atoms in the longitudinal direction \(\Delta f\) is related to the parameter \(\Delta {{v}_{z}}\) in the velocity distribution of atoms in the beam as
We note that the focal length and focusing region size in this regime are independent of the laser radiation intensity. The characteristic velocities reached in the LVIS for rubidium atoms [30] are \({{v}_{z}}\) = 14 m/s and \(\Delta {{v}_{z}}\) = 2.7 m/s. In this case, the focal length for atoms with the most probable velocity \({{v}_{z}}\) = 14 m/s at a magnetic field gradient of about g = 0.51 G/cm is 25 cm. The focusing region at these parameters has the size \(\Delta f = 4.8{\kern 1pt} \) cm.
4 FOCUSING OF THE ATOMIC BEAM INTO THE LOCALIZATION REGION OF THE U-MAGNETO-OPTICAL TRAP
The number of atoms in the U-MOT is given by Eq. (2). As mentioned above, the loading rate of atoms R is determined not by the sizes of laser beams but by the sizes of the magnetic field region where the potential has a nearly quadratic dependence on the coordinates. Estimates show that this region for the atom chip used in [16] has a diameter of about 1 mm. Consequently, the transverse dimensions of the atomic beam should be no more than 1 mm.
The transverse velocity of the atomic beam that is formed by the LVIS and has a diameter of 1 mm and an angular divergence of about 30 mrad (characteristic of the LVIS) [30] at the average longitudinal velocity \({{v}_{z}}\) = 14 m/s is \({{v}_{x}}\) = 0.22 m/s. This means that the diameter of the atomic beam at the distance \(l = 7{\kern 1pt} \) cm will be \(d = 3.2{\kern 1pt} \) mm. Some atoms of such a large atomic beam are not captured in the trap of the atom chip and the loading rate of atoms will be low. To increase the loading rate, the atomic beam should be focused.
It is easy to show that the minimum size of the localization region \({{d}_{{\min }}}\) is given by the formula
where d is the diameter of the atomic beam at the input of the 2D MOT. In the case under consideration, the length of the focusing region \(\Delta f\) is expressed in terms of the focal length f as \(\Delta f = f\Delta {{v}_{z}}{\text{/}}{{v}_{z}}\). The substitution of this expression into the above formula gives
The required minimum diameter of the localization region estimated by Eq. (6) is \({{d}_{{\min }}} \approx 310{\kern 1pt} \) μm, which is smaller than the effective trapping diameter estimated in [16].
Figure 4 shows the calculated trajectories of atoms for the case of the one-dimensional focusing of the atomic beam with an initial diameter of \({{d}_{0}} = 1{\kern 1pt} \) mm. The calculations were performed with a value of L = 2 cm accepted for the length of interaction of atoms with the 2D MOT. This focusing geometry can be ensured with standard high-vacuum elements. The saturation parameter of the atomic transition was chosen as G = 10 and the detuning was \(\delta = - 2\Gamma \). In this case, at the chosen parameters, \(\beta = - {{10}^{4}}\) s–1. The conditions accepted above to derive Eq. (4) are met for all velocities \({{v}_{z}}\) < βL = 200 m/s.
As mentioned above, at the average longitudinal and transverse velocities \({{v}_{z}}\) = 14 m/s and \({{v}_{x}}\) = 0.22 m/s, the size of the atomic beam at the input of the 2D MOT is \(d = 3.2{\kern 1pt} \) mm. The calculations were carried out for various longitudinal (\({{v}_{z}}\) = 12.7, 14, 15.4 m/s) and transverse (\({{v}_{x}}\) = 0.22, 0, –0.22 m/s) velocities of atoms (Fig. 4). It is seen in the inset, where the focusing region is shown, that atoms of different longitudinal velocity groups are focused at different distances; i.e., the lens has chromatic aberration. It is noteworthy that the condition \(\delta \gg \alpha gx + k\dot {x}\) under which Eq. (3) is derived is valid at \({{v}_{x}} < 2.5\) m/s.
Let us consider the distribution functions of atoms in the longitudinal direction along the axis of the atomic beam and in the transverse direction at the focus for the most probable velocity of atoms ( f0 = 25 cm). The number of atoms \(N(z)\) at the distance z from the 2D MOT is determined by the linear dis-tribution density function \({{F}_{z}}(z)\) normalized as \(\int_0^\infty {{{F}_{z}}} (z)dz\) = 1:
where \({{N}_{0}}\) is the number of atoms passing through the LVIS. The distribution function \({{F}_{z}}(z)\) calculated by the Monte Carlo method is shown in Fig. 5a. The width of this function shows the longitudinal focusing dimensions obtained with the Maxwellian distribution of atoms over the longitudinal velocity. The width of this distribution coincides the value calculated by Eq. (5).
(Color online) Distribution functions of atoms near the focus of the atomic lens in the (a) longitudinal and (b) transverse (at z = 25 cm) directions. The dashed line is plotted according to Eq. (7).
A similar distribution function \({{F}_{x}}(x)\) normalized as \(\int_{ - \infty }^\infty {{{F}_{x}}} (x)dx = 1\) can be introduced in the transverse direction:
The calculated distribution function \({{F}_{x}}(x)\) for the one-dimensional case is shown by the gray line in Fig. 5b. It is seen that the focusing region in the transverse direction demonstrates a pronounced maximum. About 90% of all atoms are located in a region with a size of 200 μm. The dashed line in Fig. 5b is plotted according to the following expression presented here without derivation:
where \({{v}_{0}}\) is the velocity of the atomic group that is focused at the considered longitudinal point of the transverse distribution (f0 = 25 cm in this case).
A similar distribution can also be obtained in the two-dimensional case:
About 90% of all atoms are located in a region 250 μm in diameter. In the considered approximation, an increase in the local density of atoms and, thereby, in the flux is equal to the ratio of the areas. This means that the flux of atoms in the effective localization region of the atom chip is larger than the flux of atoms in the LVIS and than the input aperture of the 2D MOT by a factor of more than 16 and about 160, respectively.
5 CONCLUSIONS
To summarize, an approach has been proposed to increase the atom loading rate into a U-magneto-optical trap of an atom chip. The approach is based on the focusing of an atomic beam by a two-dimensional magneto-optical trap located in the path of atoms from the low-velocity intense source to the atom chip. The approach based on the focusing of atoms in the localization region has some advantages compared to the approach based on the collimation of the atomic beam. Focusing makes it possible to squeeze the atomic beam in the localization region to sizes at which the magnetic field still has a quadrupole character and can localize atoms. It has shown experimentally [35] that this approach allows focusing into a region of about 270 μm, which is sufficient for increasing the loading rate of atom chips with a small localization region [16].
The focusing region of about 250 μm has been calculated disregarding the momentum diffusion of atoms at the interaction with the 2D MOT. Diffusion can be taken into account quite easily at low saturation parameters of the atomic transition. In this case, there is an analytical expression for the tensor determining the momentum diffusion coefficient [37]. However, the overdamped oscillator regime is not implemented at such parameters. To completely describe the momentum diffusion in the case under consideration, the Fokker–Planck equation should be numerically solved.
Since the atom chip operates in a periodic regime (cycle consists of loading of atoms into the trap and subsequent measurement), an increase in the loading rate allows an increase in the frequency of the loading cycle of atoms and, as a result, an increase in the accuracy of quantum sensors based on cold atoms. In addition, atom chips can be used in a number of other experiments, e.g., on the study of the spectral properties of cold atoms [38] and cold plasma [39], as well as to expand the possibility of creation of compact atomic clocks [40].
Change history
12 January 2023
An Erratum to this paper has been published: https://doi.org/10.1134/S002136402235003X
REFERENCES
R. Geiger, A. Landragin, S. Merlet, and F. Pereira Dos Santos, AVS Quantum Sci. 2, 024702 (2020).
G. M. Tino, Quantum Sci. Technol. 6, 024014 (2021).
V. Ménoret, P. Vermeulen, N. le Moigne, S. Bonvalot, P. Bouyer, A. Landragin, and B. Desruelle, Sci. Rep. 8, 12300 (2018).
D. K. Mao, X. B. Deng, H. Q. Luo, Y. Y. Xu, M. K. Zhou, X. C. Duan, and Z. K. Hu, Rev. Sci. Instrum. 92, 053202 (2021).
C. Janvier, V. Ménoret, B. Desruelle, S. Merlet, A. Landragin, and F. Pereira dos Santos, Phys. Rev. A 105, 022801 (2022).
C. L. Garrido Alzar, AVS Quantum Sci. 1, 014702 (2019).
P. Gillot, O. Francis, A. Landragin, F. Pereira Dos Santos, and S. Merlet, Metrologia 51, L15 (2014).
Y. Bidel, N. Zahzam, C. Blanchard, A. Bonnin, M. Cadoret, A. Bresson, D. Rouxel, and M. F. Lequentrec-Lalancette, Nat. Commun. 9, 627 (2018).
Y. Bidel, N. Zahzam, A. Bresson, C. Blanchard, M. Cadoret, A. V. Olesen, and R. Forsberg, J. Geodesy 94, 20 (2020).
A.-K. Cooke, C. Champollion, and N. le Moigne, Geosci. Instrum. Method. Data Syst. 10, 65 (2021).
L. Antoni-Micollier, D. Carbone, V. Ménoret, J. Lautier-Gaud, T. King, F. Greco, A. Messina, D. Contrafatto, and B. Desruelle, Earth Space Sci. OpenArchive (2022). https://doi.org/10.1002/essoar.10510251.1
B. Stray, A. Lamb, A. Kaushik, et al., Nature (London, U.K.) 602, 590 (2022).
P. Rosenbusch, Appl. Phys. B 95, 227 (2009).
P. Böhi, M. Riedel, J. Hoffrogge, J. Reichel, T. W. Hänsch, and P. Treutlein, Nat. Phys. 5, 592 (2009).
R. Szmuk, V. Dugrain, W. Maineult, J. Reichel, and P. Rosenbusch, Phys. Rev. A 92, 012106 (2015).
A. E. Afanasiev, A. S. Kalmykov, R. V. Kirtaev, A. A. Kortel, P. I. Skakunenko, D. V. Negrov, and V. I. Balykin, Opt. Laser Technol. 148, 107698 (2022).
S. Wildermuth, P. Krüger, C. Becker, M. Brajdic, S. Haupt, A. Kasper, R. Folman, and J. Schmiedmayer, Phys. Rev. A 69, 030901 (2004).
V. Singh, V. B. Tiwari, K. A. P. Singh, and S. R. Mishra, J. Mod. Opt. 65, 2332 (2018).
V. Singh, V. B. Tiwari, and S. R. Mishra, Laser Phys. Lett. 17, 035501 (2020).
S. A. Hopkins, PhD Thesis (Open Univ., Milton Keynes, UK, 1996).
C. Monroe, W. Swann, H. Robinson, and C. Wieman, Phys. Rev. Lett. 65, 1571 (1990).
A. M. Steane, M. Chowdhury, and C. J. Foot, J. Opt. Soc. Am. B 9, 2142 (1992).
J. Reichel, Appl. Phys. B 74, 469 (2002).
J. Rudolph, W. Herr, C. Grzeschik, T. Sternke, A. Grote, M. Popp, D. Becker, H. Müntinga, H. Ahlers, A. Peters, C. Lämmerzahl, K. Sengstock, N. Gaaloul, W. Ertmer, and E. M. Rasel, New J. Phys. 17, 065001 (2015).
S. Jollenbeck, J. Mahnke, R. Randoll, W. Ertmer, J. Arlt, and C. Klempt, Phys. Rev. A 83, 043406 (2011).
J. Reichel, W. Hänsel, and T. W. Hänsch, Phys. Rev. Lett. 83, 3398 (1999).
A. Golovizin, D. Tregubov, D. Mishin, D. Provorchenko, and N. Kolachevsky, Opt. Express 29, 36734 (2021).
S. Weyers, E. Aucouturier, C. Valentin, and N. Dimarcq, Opt. Commun. 143, 30 (1997).
K. Dieckmann, R. J. C. Spreeuw, M. Weidemüller, and J. T. M. Walraven, Phys. Rev. A 58, 3891 (1998).
Z. T. Lu, K. L. Corwin, M. J. Renn, M. H. Anderson, E. A. Cornell, and C. E. Wieman, Phys. Rev. Lett. 77, 3331 (1996).
V. I. Balykin, V. S. Letokhov, V. G. Minogin, Yu. V. Rozhdestvensky, and A. I. Sidorov, J. Opt. Soc. Am. B 2, 1776 (1985).
J. Nellessen, J. Werner, and W. Ertmer, Opt. Commun. 78, 300 (1990).
J. M. Kwolek, C. T. Fancher, M. Bashkansky, and A. T. Black, Phys. Rev. Appl. 13, 044057 (2020).
V. I. Balykin, JETP Lett. 66, 349 (1997).
P. N. Melentiev, P. A. Borisov, S. N. Rudnev, A. E. Afanasiev, and V. I. Balykin, JETP Lett. 83, 14 (2006).
V. I. Balykin, V. G. Minogin, and V. S. Letokhov, Rep. Prog. Phys. 63, 1429 (2000).
S. Chang and V. Minogin, Phys. Rep. 365, 65 (2002).
A. E. Afanasiev, A. M. Mashko, A. A. Meysterson, and V. I. Balykin, JETP Lett. 111, 608 (2020).
B. B. Zelener, E. V. Vilshanskaya, S. A. Saakyan, V. A. Sautenkov, B. V. Zelener, and V. E. Fortov, JETP Lett. 113, 82 (2021).
K. S. Kudeyarov, A. A. Golovizin, A. S. Borisenko, N. O. Zhadnov, I. V. Zalivako, D. S. Kryuchkov, E. O. Chiglintsev, G. A. Vishnyakova, K. Yu. Khabarova, and N. N. Kolachevsky, JETP Lett. 114, 243 (2021).
Funding
This work was supported by the Russian Science Foundation, project no. 21-12-00323 and by the Russian Foundation for Basic Research, project no. 19-29-11004.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare that they have no conflicts of interest.
Additional information
Translated by R. Tyapaev
The original online version of this article was revised: Due to a retrospective Open Access order.
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Afanasiev, A.E., Bykova, D.V., Skakunenko, P.I. et al. Focusing of an Atomic Beam for the Efficient Loading of an Atom Chip. Jetp Lett. 115, 509–517 (2022). https://doi.org/10.1134/S0021364022100496
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0021364022100496