Study of the Coherence and Entanglement of Macroscopic Quantum Interfering Alternatives

An approach has been proposed to calculate the coherence and interference characteristics of macroscopic quantum systems. A general method of the analysis of two-particle quantum systems based on the Schmidt decomposition has been presented to analyze quantum entanglement between the system and environment, as well as the coherence of interfering alternatives. Simple relations have been obtained between the coherence, interference visibility, and Schmidt number. The developed method has been applied to multimode quantum states of Schrödinger’s cat.

1 INTRODUCTION

The interference of quantum states is a key phenomenon for quantum information technologies [1]. It is observed in diverse physical systems, including diffraction gratings, biphoton fields, and two-arm electron interferometers [2]. The interaction of a quantum system with the environment results in a decoherence effect; i.e., the quantum state of the system changes uncontrollably. To take into account and to compensate decoherence in quantum computing and quantum simulators, it is important to study the coherence characteristics of various open quantum systems in the maximally general form [3–6].

One of the interfering quantum systems is Schrödinger’s cat whose quantum states are superpositions of coherent states [7] with different phases. These states are actively used in quantum optics and optical technologies [8–10], in continuous variable quantum computing [11–13], in quantum error-correction codes [14, 15], and in precise measurements [16, 17]. Multimode states formed by several subsystems (modes) are of significant practical interest. Because of the presence of entanglement, these states are universal tools for various quantum algorithms [18, 19].

The generation of multimode states of quantum Schrödinger’s cat is a very complex problem because the direct transformation of coherent states of light into the state of Schrödinger’s cat requires the creation of a medium with strong nonlinearity [20]. The scaling and generation of multimode states of Schrödinger’s cat is a very difficult problem because of the presence of decoherence. It is noteworthy that states of coherent Schrödinger’s cat for most applications should have sufficiently large average numbers of photons and modes [12, 21]. The problem of generation of multimode states of Schrödinger’s cat with a large average number of photons is important and relevant for fundamental science and for applications in metrology, quantum computing algorithms, etc.

2 MULTIMODAL STATE OF SCHRÖDINGER’S CAT

The multimode state of Schrödinger’s cat is a direct generalization of the single-mode states, which is a superposition of two coherent states whose phases differ by π (see, e.g., [22, 23]):

$${\text{|}}{{\psi }_{\alpha }}\rangle = \frac{1}{{\sqrt {2(1 + {{q}_{\alpha }})} }}({\text{|}}\alpha \rangle + \;{\text{|}} - \alpha \rangle ).$$

(1)

Here, ${{q}_{\alpha }} = \langle \alpha {\text{|}} - \alpha \rangle = \exp ( - 2{\text{|}}\alpha {{{\text{|}}}^{2}})$. In the coordinate representation, the state of Schrödinger’s cat has the form

$${{\psi }_{\alpha }}(x) = \frac{{\sqrt 2 {{C}_{\alpha }}}}{{\sqrt[4]{\pi }}}\exp \left( { - \frac{1}{2}{{x}^{2}}} \right){\text{cosh}}(\sqrt 2 \alpha x).$$

(2)

Here, ${{C}_{\alpha }} = (\exp (2{{\bar {\alpha }}^{2}}) + \exp ( - 2{{\bar {\bar {\alpha }}}^{2}}{{))}^{{ - 1/2}}}$ is the normalization constant, where $\bar {\alpha } = {\text{Re}}(\alpha )$ and $\bar {\bar {\alpha }} = {\text{Im}}(\alpha )$.

In the momentum representation, the state of Schrödinger’s cat is the Fourier transform of the state in the coordinate representation given by Eq. (2):

$${{\tilde {\psi }}_{\alpha }}(p) = \frac{{\sqrt 2 {{{\tilde {C}}}_{\alpha }}}}{{\sqrt[4]{\pi }}}\exp \left( { - \frac{1}{2}{{p}^{2}}} \right)\cos (\sqrt 2 \alpha p).$$

(3)

Here, ${{\tilde {C}}_{\alpha }} = (\exp (2{{\bar {\bar {\alpha }}}^{2}}) + \exp ( - 2{{\bar {\alpha }}^{2}}{{))}^{{ - 1/2}}}$ is the normalization constant. The constants ${{C}_{\alpha }}$ and ${{\tilde {C}}_{\alpha }}$ are transformed into each other under the replacement of ${{\bar {\alpha }}^{2}}$ by ${{\bar {\bar {\alpha }}}^{2}}$ and vice versa. In more detail, at the rotation of the coherent state by an angle of π/2, the coordinate is transformed into the momentum x → p and the a-mplitude α is transformed into a new amplitude α': α → α' = exp(iπ/2)α = iα; consequently, $\bar {\alpha }' = - \bar {\bar {\alpha }}$ and $\bar {\bar {\alpha }}' = \bar {\alpha }$. Under this transformation, the coordinate wavefunction given by Eq. (2) is transformed into the pulse wavefunction specified by Eq. (3).

The considered single-mode state can be directly generalized to a multimode case. By analogy with Eq. (1), we define the state of Schrödinger’s cat formed by n modes as

$$\begin{gathered} {\text{|}}{{\psi }_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}}\rangle = \frac{1}{{\sqrt {2\left( {1 + \prod\limits_{j = 1}^n {{q}_{{{{\alpha }_{j}}}}}} \right)} }} \\ \times \;({\text{|}}{{\alpha }_{1}},{{\alpha }_{2}}, \ldots ,{{\alpha }_{n}}\rangle + \;{\text{|}}{\kern 1pt} - {\kern 1pt} {{\alpha }_{1}}, - {{\alpha }_{2}}, \ldots , - {{\alpha }_{n}}\rangle ). \\ \end{gathered} $$

(4)

Here, ${{q}_{{{{\alpha }_{j}}}}} = \langle {{\alpha }_{j}}{\text{|}}{\kern 1pt} - {\kern 1pt} {{\alpha }_{j}}\rangle = \exp ( - 2{\text{|}}{{\alpha }_{j}}{{{\text{|}}}^{2}})$, $j = 1, \ldots ,n$. The coordinate representation of the multimode state of Schrödinger’s cat is a direct generalization of Eq. (2) for the single-mode case:

$$\begin{gathered} {{\psi }_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}}({{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{n}}) = \frac{{\sqrt 2 {{C}_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}}}}{{\sqrt[4]{{{{\pi }^{n}}}}}} \\ \times \;\exp \left( { - \frac{1}{2}\sum\limits_{j = 1}^n x_{j}^{2}} \right)\cosh \left( {\sqrt 2 \sum\limits_{j = 1}^n {{\alpha }_{j}}{{x}_{j}}} \right). \\ \end{gathered} $$

(5)

Here,

$${{C}_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}} = {{\left( {\exp \left( {2\sum\limits_{j = 1}^n \bar {\alpha }_{j}^{2}} \right) + \exp \left( { - 2\sum\limits_{j = 1}^n \bar {\bar {\alpha }}_{j}^{2}} \right)} \right)}^{{ - 1/2}}}$$

is the normalization constant, where ${{\bar {\alpha }}_{j}} = {\text{Re}}({{\alpha }_{j}})$ and ${{\bar {\bar {\alpha }}}_{j}} = {\text{Im}}({{\alpha }_{j}})$.

Similar to the coordinate representation, the momentum representation of the multimode state of Schrödinger’s cat is a direct generalization of Eq. (3) for the single-mode case:

$$\begin{gathered} {{{\tilde {\psi }}}_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}}({{p}_{1}},{{p}_{2}}, \ldots ,{{p}_{n}}) = \frac{{\sqrt 2 {{{\tilde {C}}}_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}}}}{{\sqrt[4]{{{{\pi }^{n}}}}}} \\ \times \;\exp \left( { - \frac{1}{2}\sum\limits_{j = 1}^n p_{j}^{2}} \right)\cos \left( {\sqrt 2 \sum\limits_{j = 1}^n {{\alpha }_{j}}{{p}_{j}}} \right), \\ \end{gathered} $$

(6)

where

$${{C}_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}} = {{\left( {\exp \left( {2\sum\limits_{j = 1}^n \bar {\bar {\alpha }}_{j}^{2}} \right) + \exp \left( { - 2\sum\limits_{j = 1}^n \bar {\alpha }_{j}^{2}} \right)} \right)}^{{ - 1/2}}}$$

is the normalization constant. As in the single-mode case, the normalization constants of the coordinate and momentum representations are related as ${{\tilde {C}}_{{{{\alpha }_{1}}{{\alpha }_{2}} \ldots {{\alpha }_{n}}}}} = {{C}_{{i{{\alpha }_{1}},i{{\alpha }_{2}}, \ldots ,i{{\alpha }_{n}}}}}$ and, under the rotation of the coherent state in each mode by an angle of π/2, the coordinate wavefunction given by Eq. (5) is transformed into the momentum wavefunction specified by Eq. (6).

3 STUDY OF THE COHERENCE OF STATES USING SCHMIDT EXPANSION

We separate the state given by Eq. (4) into two subsystems. The first, main, subsystem A contains the first n – m modes of the state and the second subsystem B, which is considered as the environment, consists of the remaining m modes

$$\left| {\underbrace {{{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - m}}}}_A,\overbrace {{{\alpha }_{{n - m + 1}}}, \ldots ,{{\alpha }_{n}}}^B} \right\rangle $$

$$ + \;\left| {\underbrace { - {{\alpha }_{1}}, \ldots , - {{\alpha }_{{n - m}}}}_A,\overbrace { - {{\alpha }_{{n - m + 1}}}, \ldots , - {{\alpha }_{n}}}^B} \right\rangle .$$

We consider a two-particle system consisting of the described subsystems A and B. There are two interfering alternatives ${\text{|}}{{\varphi }_{1}}\rangle = {\text{|}}{{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - m}}}\rangle$ and ${\text{|}}{{\varphi }_{2}}\rangle =$ ${\text{|}}{\kern 1pt} - {\kern 1pt} {{\alpha }_{1}}, \ldots , - {{\alpha }_{{n - m}}}\rangle$ of the first subsystem entangled with the corresponding states ${\text{|}}{{e}_{1}}\rangle = {\text{|}}{{\alpha }_{{n - m + 1}}}, \ldots ,{{\alpha }_{n}}\rangle$ and ${\text{|}}{{e}_{2}}\rangle = {\text{|}}{\kern 1pt} - {\kern 1pt} {{\alpha }_{{n - m + 1}}}, \ldots , - {{\alpha }_{n}}\rangle$ of the second subsystem representing the environment (all these states of are normalized to unity):

$${\text{|}}\psi \rangle = \frac{1}{{\sqrt {2(1 + {{q}_{1}}{{q}_{2}})} }}({\text{|}}{{\varphi }_{1}},{{e}_{1}}\rangle + \;{\text{|}}{{\varphi }_{2}},{{e}_{2}}\rangle ).$$

(7)

Here, ${{q}_{1}} = \langle {{\varphi }_{1}}{\text{|}}{{\varphi }_{2}}\rangle$ = $\exp \left( { - 2\sum\limits_{j = 1}^{n - m} {\text{|}}{{\alpha }_{j}}{{{\text{|}}}^{2}}} \right)$ is the probability amplitude of finding the alternative ${\text{|}}{{\varphi }_{1}}\rangle$ if the alternative ${\text{|}}{{\varphi }_{2}}\rangle$ was prepared. Similarly, ${{q}_{2}} = \langle {{e}_{1}}{\text{|}}{{e}_{2}}\rangle$ = $\exp \left( { - 2\sum\limits_{j = 1}^m {\text{|}}{{\alpha }_{{n - m + j}}}{{{\text{|}}}^{2}}} \right)$ is the probability amplitude of the coincidence of the environment states.

Using the Schmidt decomposition, we describe quantum entanglement between the system and environment, as well as the coherence of interfering alternatives. It is remarkable that the considered problem is reduced to the analysis of a two-qubit system irrespective of the complexity of interfering states and states of the environment. The first and second qubits specify interfering alternatives and the corresponding states of the environment. The basis states of considered qubits can be easily obtained by orthogonalization. The following logical zero and logical unity states are obtained for the qubit associated with interfering alternatives:

$${\text{|}}0{{\rangle }_{1}} = {\text{|}}{{\varphi }_{1}}\rangle , \quad {\text{|}}1{{\rangle }_{1}} = \frac{1}{{\sqrt {1 - \;{\text{|}}{{q}_{1}}{{{\text{|}}}^{2}}} }}({\text{|}}{{\varphi }_{2}}\rangle - {{q}_{1}}{\text{|}}{{\varphi }_{1}}\rangle ).$$

(8)

The corresponding states for the environment qubit have the form

$${\text{|}}0{{\rangle }_{2}} = {\text{|}}{{e}_{1}}\rangle , \quad {\text{|}}1{{\rangle }_{2}} = \frac{1}{{\sqrt {1 - \;{\text{|}}{{q}_{2}}{{{\text{|}}}^{2}}} }}({\text{|}}{{e}_{2}}\rangle - {{q}_{2}}{\text{|}}{{e}_{1}}\rangle ).$$

(9)

As a result, the two-qubit state (7) can be represented in the form

$${\text{|}}\psi \rangle = {{c}_{{00}}}{\text{|}}00\rangle + {{c}_{{01}}}{\text{|}}01\rangle + {{c}_{{10}}}{\text{|}}10\rangle + {{c}_{{11}}}{\text{|}}11\rangle .$$

(10)

Here, ${{c}_{{00}}} = \frac{{1 + {{q}_{1}}{{q}_{2}}}}{{\sqrt {2(1 + {{q}_{1}}{{q}_{2}})} }}$, ${{c}_{{01}}} = \frac{{{{q}_{1}}\sqrt {1 - \;{\text{|}}{{q}_{2}}{{{\text{|}}}^{2}}} }}{{\sqrt {2(1 + {{q}_{1}}{{q}_{2}})} }}$, c₁₀ = $\frac{{{{q}_{2}}\sqrt {1 - \;{\text{|}}{{q}_{1}}{{{\text{|}}}^{2}}} }}{{\sqrt {2(1 + {{q}_{1}}{{q}_{2}})} }}$, and ${{c}_{{11}}} = \frac{{\sqrt {(1 - \;{\text{|}}{{q}_{1}}{{{\text{|}}}^{2}})(1 - \;{\text{|}}{{q}_{2}}{{{\text{|}}}^{2}})} }}{{\sqrt {2(1 + {{q}_{1}}{{q}_{2}})} }}$.

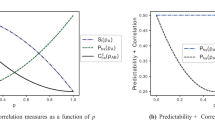
According to the above expressions, Δ = |c₀₀c₁₁ – c₀₁c₁₀|² = (1 – |q₁|²)(1 – |q₂|²)/[4(1 + q₁q₂)²]. The weights of the Schmidt decomposition λ₀ and λ₁, as well as the Schmidt number K, can be expressed in terms of the parameter Δ as

$${{\lambda }_{0}} = \frac{1}{2}(1 + \sqrt {1 - 4\Delta } ),\quad {{\lambda }_{1}} = \frac{1}{2}(1 - \sqrt {1 - 4\Delta } ),$$

(11)

$$K = \frac{1}{{\lambda _{0}^{2} + \lambda _{1}^{2}}} = \frac{1}{{1 - 2\Delta }}.$$

(12)

In the case of well-distinguished alternatives, e.g., for narrow slits in the Young experiment where q₁ = 0, we obtain Δ = (1 – |q₂|²)/4.

The notion of visibility of the interference pattern V is used to describe interference in the theory of optical phenomena [24]. The visibility of the interference pattern (for narrow slits) is defined in classical optics as

$$V = \frac{{{{I}_{{\max }}} - {{I}_{{\min }}}}}{{{{I}_{{\max }}} + {{I}_{{\min }}}}}.$$

(13)

Here, I_max and I_min are the maximum and minimum intensities of the detected optical signal, respectively. In terms of the Schmidt decomposition, the weights λ₀ and λ₁ of the fundamental (zeroth) and first modes describe the useful signal I_max and noise I_min, respectively. Consequently, the visibility is related to the Schmidt number as

$$V = {{\lambda }_{0}} - {{\lambda }_{1}} = \sqrt {\frac{{2 - K}}{K}} = \sqrt {1 - 4\Delta } .$$

(14)

The direct consideration of the interference pattern from two narrow slits [25] shows that our definition of the visibility is in agreement with the classical definition. For well-distinguished alternatives (for narrow slits in the Young experiment), when q₁ = 0, the relation between the visibility and coherence of the environment states has the simple form

$$V = {\text{|}}{{q}_{2}}{\text{|}} = {\text{|}}\langle {{e}_{1}}{\text{|}}{{e}_{2}}\rangle {\text{|}}.$$

(15)

The comparison of the presented description of interfering quantum alternatives with the classical description of coherence indicates that the scalar product of the environment states ${{q}_{2}} = \langle {{e}_{1}}{\text{|}}{{e}_{2}}\rangle$ is a natural generalization of the classical degree of coherence of light oscillations γ [24].

4 EXAMPLES OF STUDY OF COHERENCE AND INTERFERENCE

The developed mathematical technique can be applied to an arbitrarily complex system, where two different alternatives interfere. Before the application of the developed theory to multimode states of Schrödinger’s cat, we consider a classical problem of two-slit interference of polarized light beams studied by Arago and Fresnel more than 200 years ago [26]. For certainty, let the initial radiation be polarized vertically. Polarizers with the polarization axes turned by angle of θ/2 and –θ/2 from the vertical are placed in the left and right slits, respectively. Polarizers in the slits provide different effects on radiation, thus creating different polarization states of the environment |e₁〉 and |e₂〉 for interfering alternatives and inducing entanglement between the coordinate and polarization degrees of freedom of light. The angle between the directions of polarizers is θ; consequently, the degree of coherence is 〈e₁|e₂〉 = cosθ and the visibility is V  =  |〈e₁|e₂〉| = |cosθ|. Interference disappears completely (V = 0) when the angle between the polarization direction becomes right θ = π/2, which was observed in experiments by Arago and Fresnel in 1819 [26]. Although the environment states |e₁〉 and |e₂〉, as well as interfering alternatives |φ₁〉 and |φ₂〉, can be very complex, the simple formulas (14) and (15) also remain valid in the general case.

We now consider in more detail the particular case of the multimode state of Schrödinger’s cat, where the amplitudes of all modes are the same real number; i.e., α₁ = α₂ = … = α_n = α.

We perform an orthogonal transformation to new (normal) coordinates in the coordinate representation: ${{q}_{j}} = {{O}_{{jk}}}{{x}_{k}}$, $j,k = 1, \ldots ,n$. Here, O is the orthogonal matrix, where the first string consists of n identical elements equal to $1{\text{/}}\sqrt n$. The inverse transformation is specified by the matrix transposed to O: ${{x}_{j}} = O_{{jk}}^{T}{{q}_{k}}$, $j,k = 1, \ldots ,n$. Since the sum of squares of coordinates is invariant under orthogonal transformations, the wavefunction of the multimode state of Schrödinger’s cat (5) in new coordinates can be represented in the form

$$\begin{gathered} {{\psi }_{{{{\alpha }_{1}} = {{\alpha }_{2}} = \ldots {{\alpha }_{n}} = \alpha }}}({{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{n}}) \\ = {{\psi }_{{{{\alpha }_{0}}}}}({{q}_{1}})\frac{1}{{\sqrt[4]{{{{\pi }^{{n - 1}}}}}}}\exp \left( { - \frac{1}{2}\sum\limits_{j = 2}^n q_{j}^{2}} \right). \\ \end{gathered} $$

(16)

It is important that the state in new coordinates is no longer entangled. Here, ${{q}_{1}} = \frac{{{{x}_{1}} + \ldots + {{x}_{n}}}}{{\sqrt n }}$ is the first (principal) normal coordinate, ${{\psi }_{{{{\alpha }_{0}}}}}({{q}_{1}})$ is the corresponding one-dimensional state of Schrödinger’s cat (2) with the amplitude ${{\alpha }_{0}} = \alpha \sqrt n$, and the vacuum states correspond to the normal coordinates q₂, q₃, …, q_n.

The described algorithm can be used to numerically simulate complexly correlated initial multidimensional coordinates x₁, x₂, …, x_n of Schrödinger’s cat by means of the generation of independent normal coordinates q₁, q₂, …, q_n with their subsequent orthogonal transformation. In this case, the random variable q₁ corresponds to the one-dimensional distribution of Schrödinger’s cat with the amplitude ${{\alpha }_{0}} = \alpha \sqrt n$, whereas the remaining coordinates q₂, q₃, …, q_n are Gaussian random variables with zero mean value and variance σ² = 1/2 corresponding to the variance of vacuum fluctuations.

The considered one-dimensional state of Schrödinger’s cat ${{\psi }_{{{{\alpha }_{0}}}}}({{q}_{1}})$ can be represented in the form

$${{\psi }_{{{{\alpha }_{0}}}}}({{q}_{1}}) = \frac{1}{{\sqrt 2 \sqrt[4]{\pi }\sqrt {1 + \exp ( - 2{{\alpha }^{2}}n)} }}$$

$$ \times \;\left[ {\exp \left( { - \frac{1}{2}{{{({{q}_{1}} - \sqrt 2 \alpha \sqrt n )}}^{2}}} \right)} \right.$$

(17)

$$ + \;\left. {\exp \left( { - \frac{1}{2}{{{({{q}_{1}} + \sqrt 2 \alpha \sqrt n )}}^{2}}} \right)} \right].$$

We conditionally suggest that the first and second terms in Eq. (17) correspond to the “alive” and “dead” states of Schrödinger’s cat, respectively. The probability distribution corresponding to the wavefunction (17) has the form

$$\begin{gathered} {{P}_{{{{\alpha }_{0}}}}}({{q}_{1}}) = \frac{1}{{\sqrt \pi (1 + \exp ( - 2{{\alpha }^{2}}n))}} \\ \times \;\left\lfloor {\frac{1}{2}{{e}^{{ - {{{({{q}_{1}} - \sqrt 2 \alpha \sqrt n )}}^{2}}}}} + \frac{1}{2}{{e}^{{ - {{{({{q}_{1}} + \sqrt 2 \alpha \sqrt n )}}^{2}}}}} + {{e}^{{ - (q_{1}^{2} + 2{{\alpha }^{2}}n)}}}} \right\rfloor . \\ \end{gathered} $$

(18)

In the context of the problem under consideration, the case where each mode carries a small number of photons (α² ≪ 1) but the total number of photons is large (nα² ≫ 1) is the most interesting. Let α = 0.01 and n = 10⁶; then, exp(–2nα²) = exp(–200) = 1.38 × 10^–87 is a vanishingly small value. This corresponds to the approximation of well-distinguished alternatives in Eq. (17). In this case, according to Eq. (18), the probability distribution for q₁ is the sum of two Gaussian distributions with the same weights, the same variance σ² = 1/2, and mean values of $\pm \sqrt 2 \alpha \sqrt n$, where the signs + and – correspond to the alive and dead states of Schrödinger’s cat, respectively. When $\alpha \sqrt n \gg 1$, the considered alternatives can be well distinguished between each other if the quantity q₁ is determined by measuring the sum coordinate in all n modes. Ho-wever, when the number of modes is macroscopic, it is not necessary to measure all n modes and it is sufficient to measure only a limited number of modes m ≪ n such that $\alpha \sqrt m \sim 1$. In this case, the sum coordinate in the limited system of m modes will make it possible to predict the sum coordinate in the entire system of n modes (i.e., to estimate whether the cat is alive or dead). This is possible because of the strong correlation relation between the considered quantities. To analyze the desired correlation relations between subsystems, we perform the orthogonal transformation to the normal coordinates for subsystems A and B considered above. For the subsystem A in the coordinate representation, $q_{j}^{A} = O_{{jk}}^{A}{{x}_{k}}$, $j,k = 1, \ldots ,n - m$. Here, O^A is the orthogonal matrix acting in the subsystem A, where the first string consists of n – m identical elements $1{\text{/}}\sqrt {n - m}$. Similarly, for the subsystem B in the coordinate representation, $q_{j}^{B} = O_{{jk}}^{B}{{x}_{{n - m + k}}}$, $j,k = 1, \ldots ,m$. Here, O^B is the orthogonal matrix acting in the subsystem B, where the first string consists of m identical elements $1{\text{/}}\sqrt m$.

Note that orthogonal transformations in the subsystems A and B in the case under consideration are local transformations that act only inside subsystems and do not change the entanglement characteristics between considered subsystems themselves. The wavefunction of the multimode state of Schrödinger’s cat (5) can be represented in new coordinates in the form

$$\psi _{{{{\alpha }_{1}} = {{\alpha }_{2}} = \ldots {{\alpha }_{n}} = \alpha }}^{{A,B}}(q_{1}^{A},...,q_{{n - m}}^{A};q_{1}^{B},...,q_{m}^{B})$$

$$ = {{\psi }_{{\alpha _{0}^{A}\alpha _{0}^{B}}}}(q_{1}^{A},q_{1}^{B})\frac{1}{{\sqrt[4]{{{{\pi }^{{n - 2}}}}}}}$$

(19)

$$ \times \;\exp \left( { - \frac{1}{2}\sum\limits_{j = 2}^{n - m} {{{(q_{j}^{A})}}^{2}}} \right)\exp \left( { - \frac{1}{2}\sum\limits_{j = 2}^m {{{(q_{j}^{B})}}^{2}}} \right).$$

The entanglement of a state in new coordinates is determined by the quantities $q_{1}^{A} = \frac{{{{x}_{1}} + \ldots + {{x}_{{n - m}}}}}{{\sqrt {n - m} }}$ and $q_{1}^{B} = \frac{{{{x}_{{n - m + 1}}} + \ldots + {{x}_{n}}}}{{\sqrt m }}$, which are the first (principal) normal coordinates in the subsystems A and B, respectively. They correspond to the two-dimensional state ${{\psi }_{{\alpha _{0}^{A}\alpha _{0}^{B}}}}(q_{1}^{A},q_{1}^{A})$ of Schrödinger’s cat with the amplitudes $\alpha _{0}^{A} = \alpha \sqrt {n - m}$ and $\alpha _{0}^{B} = \alpha \sqrt m$ (the explicit form of this state can be easily determined using Eq. (5)). The remaining n – 2 normal coordinates $q_{2}^{A}, \ldots ,q_{{n - m}}^{A};q_{2}^{B}, \ldots ,q_{m}^{B}$ in Eq. (19) correspond to vacuum states.

The considered two-dimensional state of Schrödinger’s cat can also be represented in the form

$${{\psi }_{{\alpha _{0}^{A}\alpha _{0}^{B}}}}(q_{1}^{A},q_{1}^{B}) = \frac{1}{{\sqrt {2\pi } \sqrt {1 + \exp ( - 2{{\alpha }^{2}}n)} }}$$

$$ \times \;\left[ {\exp \left( { - \frac{1}{2}{{{(q_{1}^{A} - \sqrt 2 \alpha _{0}^{A})}}^{2}}} \right)} \right.\exp \left( { - \frac{1}{2}{{{(q_{1}^{B} - \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)$$

(20)

$$ + \;\exp \left( { - \frac{1}{2}{{{(q_{1}^{A} + \sqrt 2 \alpha _{0}^{A})}}^{2}}} \right)\exp \left. {\left( { - \frac{1}{2}{{{(q_{1}^{B} + \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)} \right].$$

This formula clearly represents quantum entanglement between the variables $q_{1}^{A}$ and $q_{1}^{B}$ corresponding to the state of the cat and environment, respectively. The observation of the environment variable $q_{1}^{B}$ near $\sqrt 2 \alpha _{0}^{B} = \sqrt 2 \alpha \sqrt m$ and $- \sqrt 2 \alpha _{0}^{B} = - \sqrt 2 \alpha \sqrt m$ corresponds to the detection of the alive and dead states of the cat, respectively.

The probability amplitudes of observations of the  alive and dead states of the cat in Eq. (20) are p-roportional to $\exp \left( { - \frac{1}{2}{{{(q_{1}^{B}\, - \,\sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)$ and $\exp \left( { - \frac{1}{2}{{{(q_{1}^{B}\, + \,\sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)$, respectively. Then, the probabilities of the “survival” P₀ and “death” P₁ of the cat are given by the expressions

$$\begin{gathered} {{P}_{0}} = \frac{{\exp \left( { - {{{(q_{1}^{B} - \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)}}{{\exp \left( { - {{{(q_{1}^{B} - \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right) + \exp \left( { - {{{(q_{1}^{B} + \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)}}, \\ {{P}_{1}} = \frac{{\exp \left( { - {{{(q_{1}^{B} + \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)}}{{\exp \left( { - {{{(q_{1}^{B} - \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right) + \exp \left( { - {{{(q_{1}^{B} + \sqrt 2 \alpha _{0}^{B})}}^{2}}} \right)}}. \\ \end{gathered} $$

(21)

The corresponding probabilities are specified by the first normal coordinate of the environment $q_{1}^{B} =$ $\frac{{{{x}_{{n - m + 1}}} + \ldots + {{x}_{n}}}}{{\sqrt m }}$, which is in turn determined by the sum coordinate of all measured environment modes.

We introduce the notion of “health” H of multimode Schrödinger’s cat by the formula

$$H(m) = \ln \left( {\frac{{{{P}_{0}}}}{{{{P}_{1}}}}} \right).$$

(22)

According to Eqs. (21) and (22), the health of multimode Schrödinger’s cat is determined by the sum of all measured environment modes:

$$H(m) = 4\alpha \sqrt 2 \sum\limits_{j = 1}^m {{x}_{{n - m + j}}}.$$

(23)

The introduced parameter specifies the level of “collapse” to the quantum state of Schrödinger’s cat. The value H = 0 obviously corresponds to P₀ = P₁ = 0.5 and the maximum coherence between subsystems. Further, if H → +∞ (at n → ∞ and m → ∞), P₀ → 1 (collapse to the alive state of the cat) and, on the contrary, if H → –∞ under the same conditions, P₀ → 0 (collapse to the dead state of the cat).

Figure 1 shows the dependence of the (a) survival probability and (b) health parameter H for multimode Schrödinger’s cat on the number of measured environment modes m. It is seen that the superposition of the alive and dead states of the cat is almost completely destroyed beginning approximately with m = 1.5 × 10⁴ (corresponding to mα² = 1.5 photons). It is seen that the multimode quantum state of Schrödinger’s cat is practically unstable because the reduction of only one or two photons almost completely destroys the coherence of the initial quantum state.

Fig. 1.

(Color online) (a) Survival probability of Schrödinger’s cat and (b) the health parameter of Schrödinger’s cat versus the number of reduced modes at α = 0.01 and n = 10⁶ according to 30 numerical experiments.

The structure of the state (20) fully corresponds to the structure of the two-particle state (7), where ${{q}_{1}} = \langle {{\varphi }_{1}}{\text{|}}{{\varphi }_{2}}\rangle$ = $\exp ( - 2{{\alpha }^{2}}(n - m))$ and ${{q}_{2}} = \langle {{e}_{1}}{\text{|}}{{e}_{2}}\rangle$ = $\exp ( - 2{{\alpha }^{2}}m)$. When the number of modes n is macroscopically large, the parameter q₁ is vanishingly small and the visibility of the interference pattern is

$$V = {\text{|}}\langle {{e}_{1}}{\text{|}}{{e}_{2}}\rangle {\text{|}} = \exp ( - 2{{\alpha }^{2}}m).$$

(24)

According to Eq. (24), when the average number of photons in each mode is negligibly small (α² is very small), states of a very large number of modes can be destroyed without a significant effect on coherence and interference. However, when the average total photons collected in decoherence modes becomes about one photon (α²m ~1), the superposition of macroscopic alternatives becomes hardly visible. In this sense, the original idea of Schrödinger’s cat [27] on the possible decisive effect of an individual microparticle on the destiny of a macroscopic object is valid.

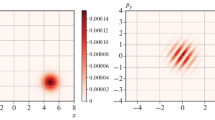
To clearly represent interference, it is convenient to pass from the coordinate representation to the momentum representation by changing α to iα. We introduce the main component associated with interference in the form

$$x = \frac{{{{p}_{1}} + \ldots + {{p}_{{n - m}}}}}{{\sqrt {n - m} }}.$$

(25)

Integration over the variable of the environment gives its distribution in the following form, which ensures interference:

$$\begin{gathered} \tilde {P}(x) = \frac{1}{{(1 + \exp ( - 2n{{\alpha }^{2}}))\sqrt \pi }} \\ \times \;\exp ( - {{x}^{2}})\left[ {1 + V\cos (2\sqrt 2 \alpha \sqrt {n - m} x)} \right]. \\ \end{gathered} $$

(26)

Here, visibility is specified by Eq. (24). The considered phenomenon is illustrated in Fig. 2, which demonstrates good agreement between the theory specified by Eq. (26) and the numerical simulation according to the method presented above.

Fig. 2.

(Color online) Interference patterns at α = 0.01 and n = 10⁶ for various numbers of reduced modes according to (histograms) numerical experiments with a sample volume of 2 × 10⁵ and (line) theory.

5 CONCLUSIONS

To summarize, a mathematical technique has been proposed and studied to analyze systems with interfering alternatives. A general method of the analysis of two-particle quantum systems based on the Schmidt decomposition has been presented to analyze quantum entanglement between the system and environment, as well as the coherence of interfering alternatives. Simple relations have been obtained between the coherence, interference visibility, and Schmidt number. As an illustration, we have studied the coherence and interference of the multimode quantum states of Schrödinger’s cat. It has been shown that decoherence of multimode states is brightly manifested in the presence of many modes where the average number of photons in each of the modes is much smaller unity. Hypothetically, macroscopically distinguished interfering alternatives in the multimode state of Schrödinger’s cat can be characterized by arbitrarily high total energy and total number of photons. However, such macroscopically distinguished superpositions are almost completely destroyed already at the observation of a limited number of modes of the environment, which totally include about one photon. Thus, the destiny of legendary Schrödinger’s cat depends not on a macroscopic observer, but on microscopic processes that affect a limited number of modes of the environment and constitute a negligibly small fraction of the initial multimode state.