1 INTRODUCTION

The quantum condensate mechanism of the origin of the mass of the Higgs boson without the explicit breaking of conformal symmetry was proposed in [1]. In this mechanism, the condensate of top quarks replaces a tachyon mass term in the phenomenological Higgs potential. The magnitude of the quark condensate cannot be calculated directly in QCD because the corresponding integrals converge and require renormalizations involving some additional conditions, e.g., experimental data. The nontrivial topology of space can specify the renormalization condition necessary in calculations. There are different effective methods of regularization and renormalization of ultraviolet divergences [2]. The first such consistent method was developed by Ya.B. Zel’dovich and A.A. Starobinskii [3] in a more general case of the Bianchi type-I anisotropic cosmological model, which coincides with a method later proposed in [4]. For the topological Casimir effect, the finite magnitude of the fermion condensate can be extracted by the subtraction of the corresponding divergent integral defined in the tangent Minkowski space from the divergent sum defined in the Friedmann spacetime. To this end, the Abel–Plana formula from the theory of analytical functions, which was applied in a cosmological context for the first time in [5]; see also [6]. The Casimir condensate of the conformal massive scalar field in the compact Friedmann universe in the static approximation was previously calculated in [7].

2 CONFORMAL MASSIVE BISPINOR FIELD

The conformal spacetime metric of the Friedmann universe \(\mathcal{M} = {{\mathbb{R}}^{1}} \times {{S}^{3}}\) has the form

$$\begin{gathered} d{{s}^{2}} \\ = {{a}^{2}}(\eta )\left( { - d{{\eta }^{2}} + d{{\chi }^{2}} + {{{\sin }}^{2}}\chi (d{{\theta }^{2}} + {{{\sin }}^{2}}\theta d{{\phi }^{2}})} \right), \\ \end{gathered} $$
(1)

where η is the conformal time, \(a(\eta )\) is the conformal scaling factor having the meaning of the radius of a three-dimensional sphere \({{S}^{3}}\), and χ, θ, and ϕ are the angular coordinates of the sphere. Let us perform a transformation to the conformal metric \({{\tilde {g}}_{{\mu \nu }}}(x)\) and conformal bispinor field \(\tilde {\psi }(x)\) according to their conformal weights:

$$\begin{gathered} {{g}_{{\mu \nu }}}(x) = {{\left( {a(\eta ){\text{/}}{{a}_{0}}} \right)}^{2}}{{{\tilde {g}}}_{{\mu \nu }}}(x), \\ \psi (x) = {{\left( {{{a}_{0}}{\text{/}}a(\eta )} \right)}^{{3/2}}}\tilde {\psi }(x). \\ \end{gathered} $$
(2)

The canonical Hamiltonian of particles with an increasing mass in the static space leads to a finite density of created particles [8]. The modern Hubble diagram is interpreted in conformal variables without the introduction of the so-called dark energy [9, 10]. The static spacetime interval corresponds to the Universe with the modern radius \({{a}_{0}}\)

$$d{{\tilde {s}}^{2}} = a_{0}^{2}( - d{{\eta }^{2}} + d{{\chi }^{2}} + {{\sin }^{2}}\chi (d{{\theta }^{2}} + {{\sin }^{2}}\theta d{{\phi }^{2}}))$$
(3)

with the curvature \(\tilde {R} = 6{\text{/}}a_{0}^{2}\). Change to the conformal variables leads to observables with a regular behavior at a = 0. The problem is now formulated for the bispinor field with the mass ma in the static Einstein universe \({{\mathbb{R}}^{1}} \times {{S}^{3}}\), where \({{S}^{3}}\) is the sphere with the radius a0.

The Dirac equation for the massive bispinor field \(\psi (x)\) in the Friedmann spacetime [2] has the form

$${{\gamma }^{0}}\left( {\frac{\partial }{{\partial \eta }} + \frac{{3a{\kern 1pt} '}}{{2a}}} \right)\psi (x) + {{\gamma }^{1}}\left( {\frac{\partial }{{\partial \chi }} + \cot \chi } \right)\psi (x)$$
$$ + \;{{\gamma }^{2}}\frac{1}{{\sin \chi }}\left( {\frac{\partial }{{\partial \theta }} + \frac{1}{2}\cot \theta } \right)\psi (x)$$
(4)
$$ + \;{{\gamma }^{3}}\frac{1}{{\sin \chi \sin \theta }}\frac{\partial }{{\partial \phi }}\psi (x) + iam\psi (x) = 0,$$

where γi, i = 0–3 are the Dirac matrices in the standard representation, and the prime stands for the differentiation with respect to the conformal time η. To separate variables, we use the ansatz [6]

$${{\tilde {\psi }}_{J}}(x) = \left( {\begin{array}{*{20}{c}} {{{f}_{{\lambda + }}}(\eta )I}&0 \\ 0&{{{f}_{{\lambda - }}}(\eta )I} \end{array}} \right){{N}_{J}}(\chi ,\theta ,\phi ),$$
(5)

where I is the 2 × 2 identity matrix, \({{N}_{J}}(\chi ,\theta ,\phi ) = ({{N}_{1}},{{N}_{2}},{{N}_{3}},{{N}_{4}}{{)}^{T}}\) is the bispinor with a combined subscript \(J \equiv \{ \lambda ,j,l,M\} \):

$$\begin{array}{*{20}{c}} {\lambda = 3{\text{/}}2,5{\text{/}}2, \ldots ;\quad j = 1{\text{/}}2,3{\text{/}}2, \ldots ,} \\ {\lambda - 1;\quad l = j \pm 1{\text{/}}2;\quad - {\kern 1pt} j \leqslant M \leqslant j.} \end{array}$$
(6)

The variables \({{f}_{{\lambda + }}}\) and \({{f}_{{\lambda - }}}\) as functions of the conformal time satisfy the second-order oscillator equations

$$\begin{array}{*{20}{c}} {f_{{\lambda \pm }}^{{''}} + \left( {\omega _{\lambda }^{2}(\eta ) \pm ima{\kern 1pt} '(\eta )} \right){{f}_{{\lambda \pm }}} = 0,} \\ {{{\omega }^{2}}(\eta ) \equiv {{\lambda }^{2}} + {{m}^{2}}{{a}^{2}}(\eta ).} \end{array}$$
(7)

The substitution of Eq. (5) into the Dirac equation (4) gives

$$ - i\lambda \left( {\begin{array}{*{20}{c}} I&0 \\ 0&{ - I} \end{array}} \right){{N}_{J}} + \;\left( {\begin{array}{*{20}{c}} 0&{{{\sigma }_{1}}} \\ { - {{\sigma }_{1}}}&0 \end{array}} \right)\left( {\frac{\partial }{{\partial \chi }} + \cot \chi } \right){{N}_{J}}$$
$$ + \;\frac{1}{{\sin \chi }}\left( {\begin{array}{*{20}{c}} 0&{{{\sigma }_{2}}} \\ { - {{\sigma }_{2}}}&0 \end{array}} \right)\left( {\frac{\partial }{{\partial \theta }} + \frac{1}{2}\cot \theta } \right){{N}_{J}}$$
$$ + \;\frac{1}{{\sin \chi \sin \theta }}\left( {\begin{array}{*{20}{c}} {0{{\sigma }_{3}}}&{} \\ { - {{\sigma }_{3}}}&0 \end{array}} \right)\frac{{\partial {{N}_{J}}}}{{\partial \phi }} = 0,$$

where σi, i = 1–3 are the Pauli matrices.

3 CASIMIR CONDENSATE OF THE MASSIVE BISPINOR FIELD

To estimate the vacuum average of the fermion field (its condensate), we expand the field operator in the form of a complete set of eigenspinors with positive and negative frequencies. Then, the quantum field operator is represented as the sum

$$\tilde {\psi }(x) = \sum\limits_J \left( {\tilde {\psi }_{J}^{{( + )}}(x){{{\hat {a}}}_{J}} + \tilde {\psi }_{J}^{{( - )}}(x)\hat {b}_{J}^{ + }} \right).$$
(8)

Here, \({{\hat {a}}_{J}}\) is the annihilation operator of a particle and \(\hat {b}_{J}^{ + }\) is the creation operator of an antiparticle. We define the quantum Casimir condensate as a vacuum average of two operators at one point. Using the standard anticommutation relations, we arrive at the following formula for the sum of the modes:

$$\begin{gathered} \langle 0{\text{|}}\bar {\tilde {\psi }}(x)\tilde {\psi }(x){\text{|}}0\rangle = \sum\limits_J \bar {\tilde {\psi }}_{J}^{{( - )}}(x)\tilde {\psi }_{J}^{{( - )}}(x) \\ = \sum\limits_J \psi {{_{J}^{{( - )}}}^{ + }}(x){{\gamma }^{0}}\psi _{J}^{{( - )}}(x), \\ \end{gathered} $$
(9)

where \(\bar {\psi } \equiv {{\psi }^{ + }}{{\gamma }^{0}}.\) According to Eq. (9), the Casimir condensate is formed by virtual antiparticles. Sum (9) can be represented in the matrix form

$$\begin{gathered} \sum\limits_J N_{J}^{ + }(\chi ,\theta ,\phi )\left( {\begin{array}{*{20}{c}} {f_{{\lambda + }}^{{( - )}}(\eta )I}&0 \\ 0&{f_{{\lambda - }}^{{( - )}}(\eta )I} \end{array}} \right){{\gamma }^{0}} \\ \times \;\left( {\begin{array}{*{20}{c}} {f_{{\lambda + }}^{{( - )}}(\eta )I}&0 \\ 0&{f_{{\lambda - }}^{{( - )}}(\eta )I} \end{array}} \right){{N}_{J}}(\chi ,\theta ,\phi ). \\ \end{gathered} $$
(10)

We consider only the statistical contribution to the quantum condensate and the quasistatic state \((a{\kern 1pt} ' = 0)\) [2]. Solutions with positive and negative frequencies have the form

$$\begin{array}{*{20}{c}} {f_{{\lambda \pm }}^{{( + )}}(\eta ) = \pm \sqrt {\frac{{\omega \mp ma}}{\omega }} {{e}^{{i\omega \eta }}},} \\ {f_{{\lambda \pm }}^{{( - )}}(\eta ) = \sqrt {\frac{{\omega \pm ma}}{\omega }} {{e}^{{ - i\omega \eta }}}.} \end{array}$$
(11)

Solutions with negative frequencies in Eqs. (11) satisfy the equality

$${\text{|}}f_{{\lambda + }}^{{( - )}}{{{\text{|}}}^{2}} - \;{\text{|}}f_{{\lambda - }}^{{( - )}}{{{\text{|}}}^{2}} = 2ma{\text{/}}\omega .$$
(12)

For further calculations of the quantum condensate, we apply the formula of summation over quantum numbers:

$$\sum\limits_{j,l,M} \psi {{_{J}^{{( \pm )}}}^{ + }}(x)\psi _{J}^{{( \pm )}}(x) = \frac{1}{{{{\pi }^{2}}{{a}^{3}}}}\left( {{{\lambda }^{2}} - \frac{1}{4}} \right).$$
(13)

Summing over quantum numbers, we obtain the divergent series

$$\langle 0{\text{|}}\bar {\tilde {\psi }}(x)\tilde {\psi }(x){\text{|}}0\rangle = \frac{{ma}}{{{{\pi }^{2}}}}\sum\limits_{\lambda = 3/2,5/2, \ldots }^\infty \frac{{{{\lambda }^{2}} - 1{\text{/}}4}}{{\sqrt {{{\lambda }^{2}} + {{m}^{2}}{{a}^{2}}} }}.$$
(14)

The Abel–Plana formula for the renormalization of an analytical function [2]

$$\begin{gathered} {\text{ren}}\sum\limits_{\lambda = 0}^\infty F(\lambda + 1{\text{/}}2) \equiv \sum\limits_{\lambda = 0}^\infty F(\lambda + 1{\text{/}}2) \\ - \;\int\limits_0^\infty dt{\kern 1pt} F(t) = - i\int\limits_0^\infty dt\frac{{F(it) - F( - it)}}{{\exp (2\pi t) + 1}} \\ \end{gathered} $$
(15)

is used in the case of summation over half-integers. In the three-dimensional Euclidean space tangent to \({{S}^{3}}\), the topological Casimir effect leads to the renormalized result in the form of the convergent integral:

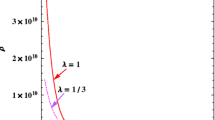
$$\begin{gathered} \tilde {c}: = {{\langle 0{\text{|}}\bar {\tilde {\psi }}(x)\tilde {\psi }(x){\text{|}}0\rangle }^{{{\text{ren}}}}} \\ = 2\frac{{ma}}{{{{\pi }^{2}}}}\int\limits_{ma}^\infty \frac{{d\lambda {\kern 1pt} ({{\lambda }^{2}} + 1{\text{/}}4)}}{{\sqrt {{{\lambda }^{2}} - {{m}^{2}}{{a}^{2}}} (\exp (2\pi \lambda ) + 1)}}. \\ \end{gathered} $$
(16)

Here, the lower integration limit is the dimensionless fermion mass ma depending on the scaling factor. The dependence of the conformal Casimir condensate \(\tilde {c} = \tilde {c}(ma)\) on this mass is shown in Fig. 1.

Fig. 1.
figure 1

(Color online) Casimir condensate of the massive fermion field versus the variable mass of the particle ma.

Full size image

4 CONCLUSIONS

To summarize, we have calculated the condensate of the bispinor field in the Friedmann universe as a function of the scaling factor. The Casimir topological conditions in the chosen metric have made it possible to renormalize a divergent series and to obtain a particular final answer for the desired quantity. The calculations have been performed with the methods described in [6] and supplement the results reported in [6]. The result obtained in this work will be used to describe the evolution of fields in the early Universe. It is impossible to directly use our result to calculate quark condensates in QCD because the dynamics of strong interactions and breaking of conformal invariance should be taken into account in this case.